Patents
Literature
Hiro is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
155results about How to "Performed quickly" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
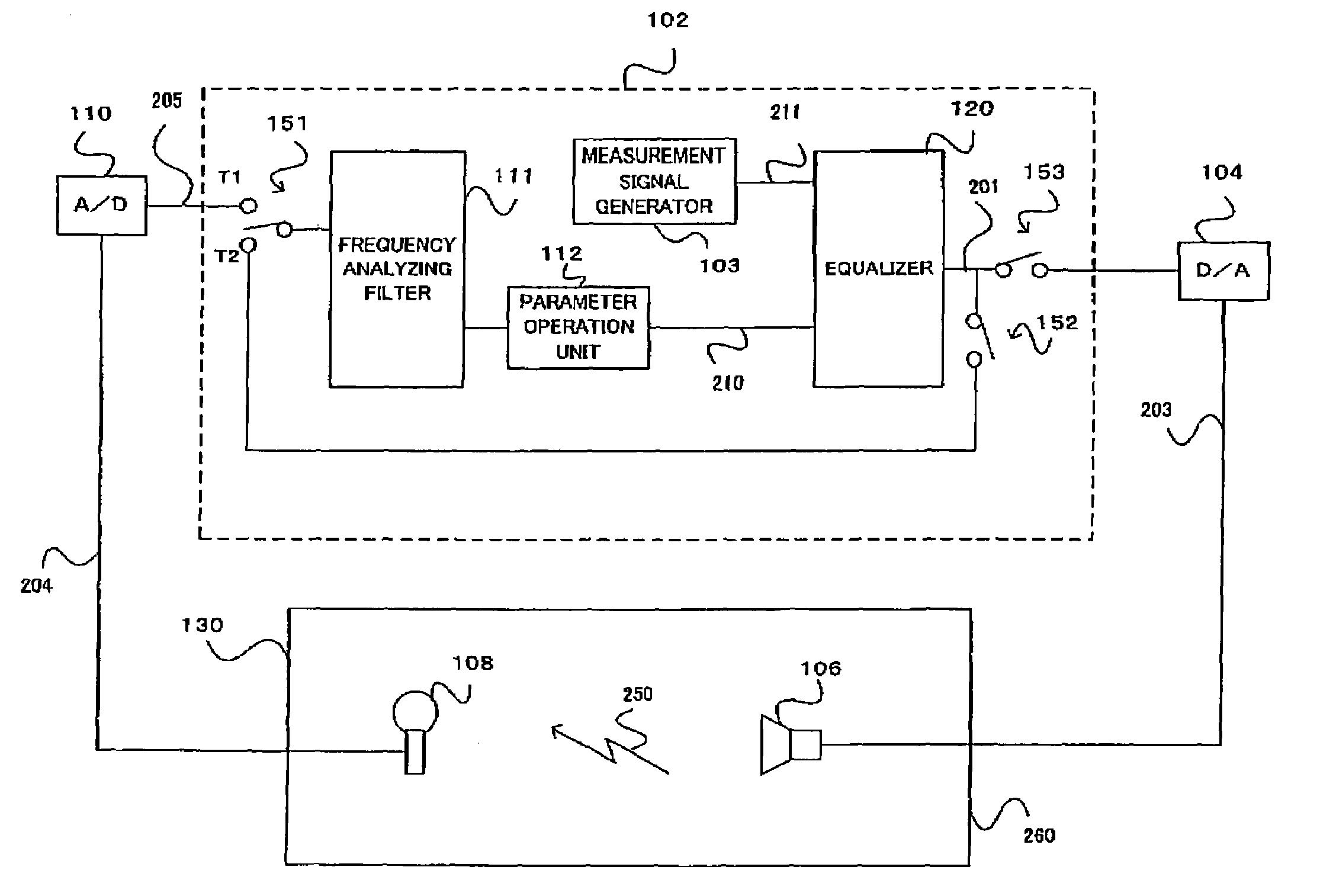
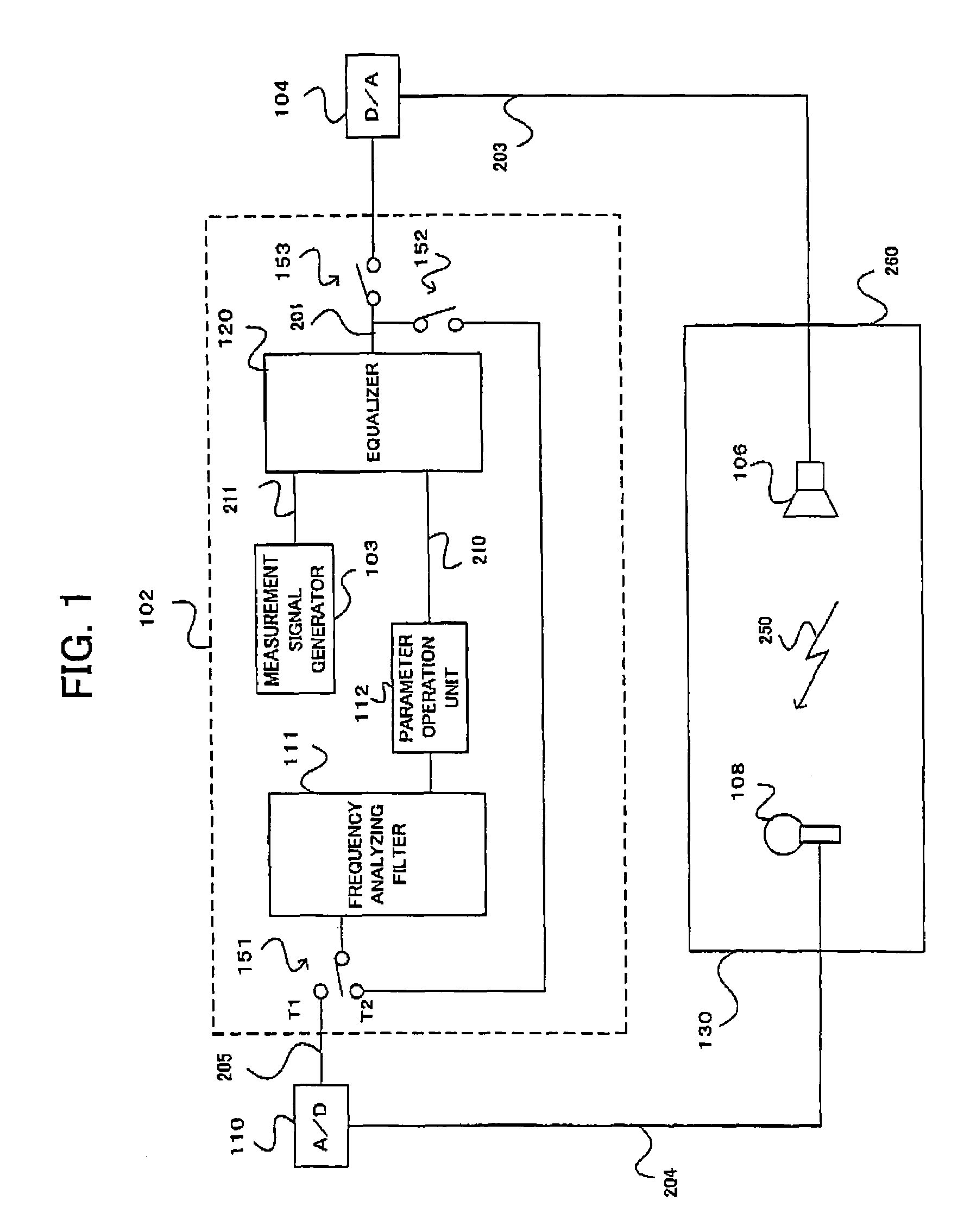
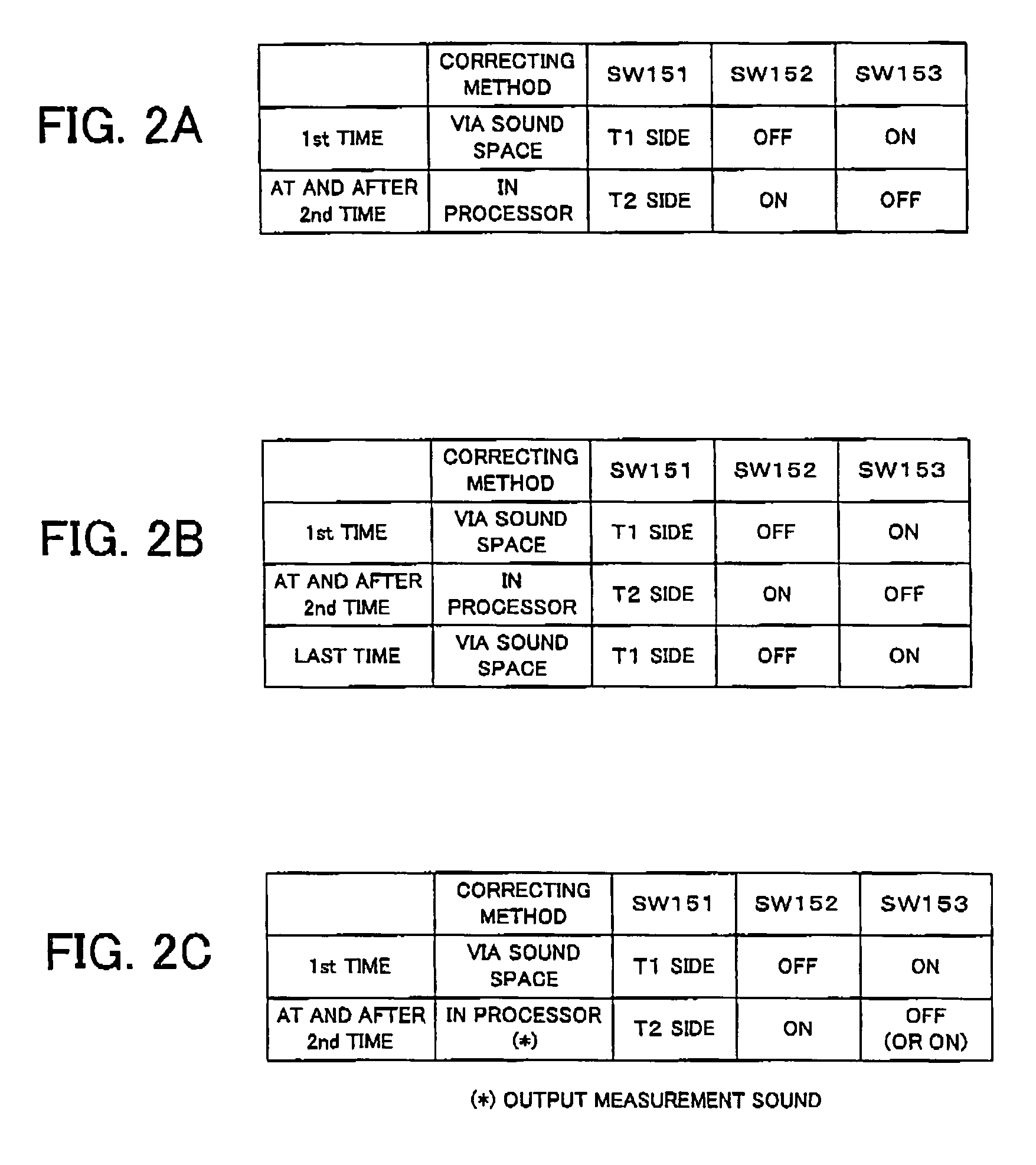
Automatic sound field correcting device and computer program therefor
InactiveUS7489784B2Performed quicklyReduce processing timePseudo-stereo systemsFrequency response correctionSignal processing circuitsLoudspeaker
An automatic sound field correcting device executes a signal process to the plurality of audio signals on respective correspondent signal transmission paths, and outputs them to a plurality of correspondent speakers to correct sound characteristics on the respective signal transmission paths. Namely, a measurement signal is supplied to each signal transmission path, and a measurement sound corresponding to it is outputted from the speaker to a sound space. The outputted measurement sound is detected as a detecting signal. The frequency characteristic of the audio signal on each signal transmission path is corrected by an equalizer, and a gain value of the equalizer is determined by a correction amount determining unit. A frequency characteristics correction is performed predetermined times. At a first correction, the correction amount determining unit determines the correction amount by performing a frequency analysis, based on the detecting signal, i.e. base on the detecting signal corresponding to the measurement sound actually outputted to the sound space. On the contrary, at and after a second correction, the correction amount determining unit determines the correction amount based on the detecting signal or an output signal of the equalizer. Namely, at and after the second correction, the output signal of the equalizer is supplied to the correction amount determining unit in a signal processing circuit as the need arises, and the frequency characteristics correction is performed without actually outputting the measurement sound to the sound space.
Owner:ONKYO KK D B A ONKYO CORP
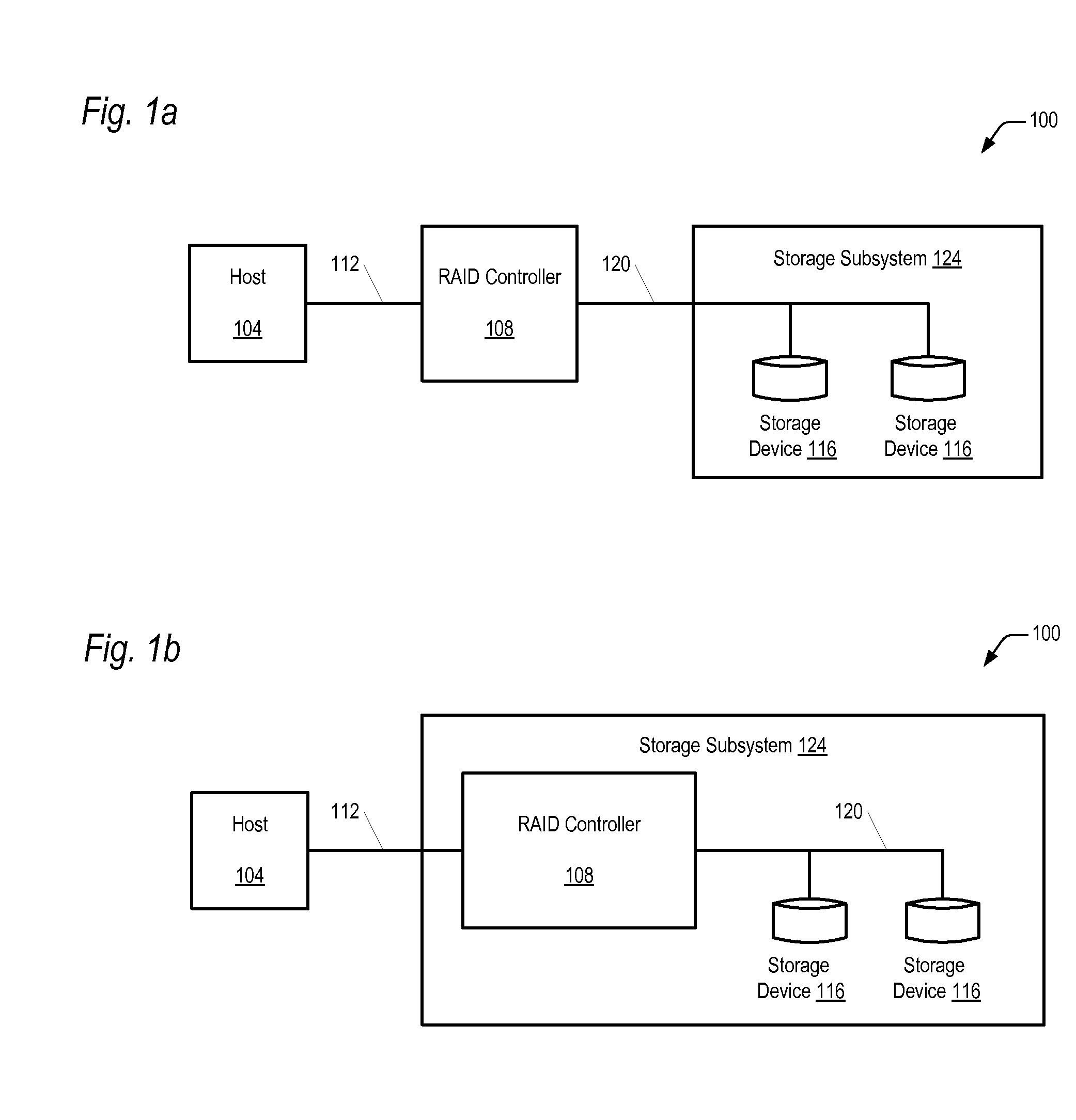
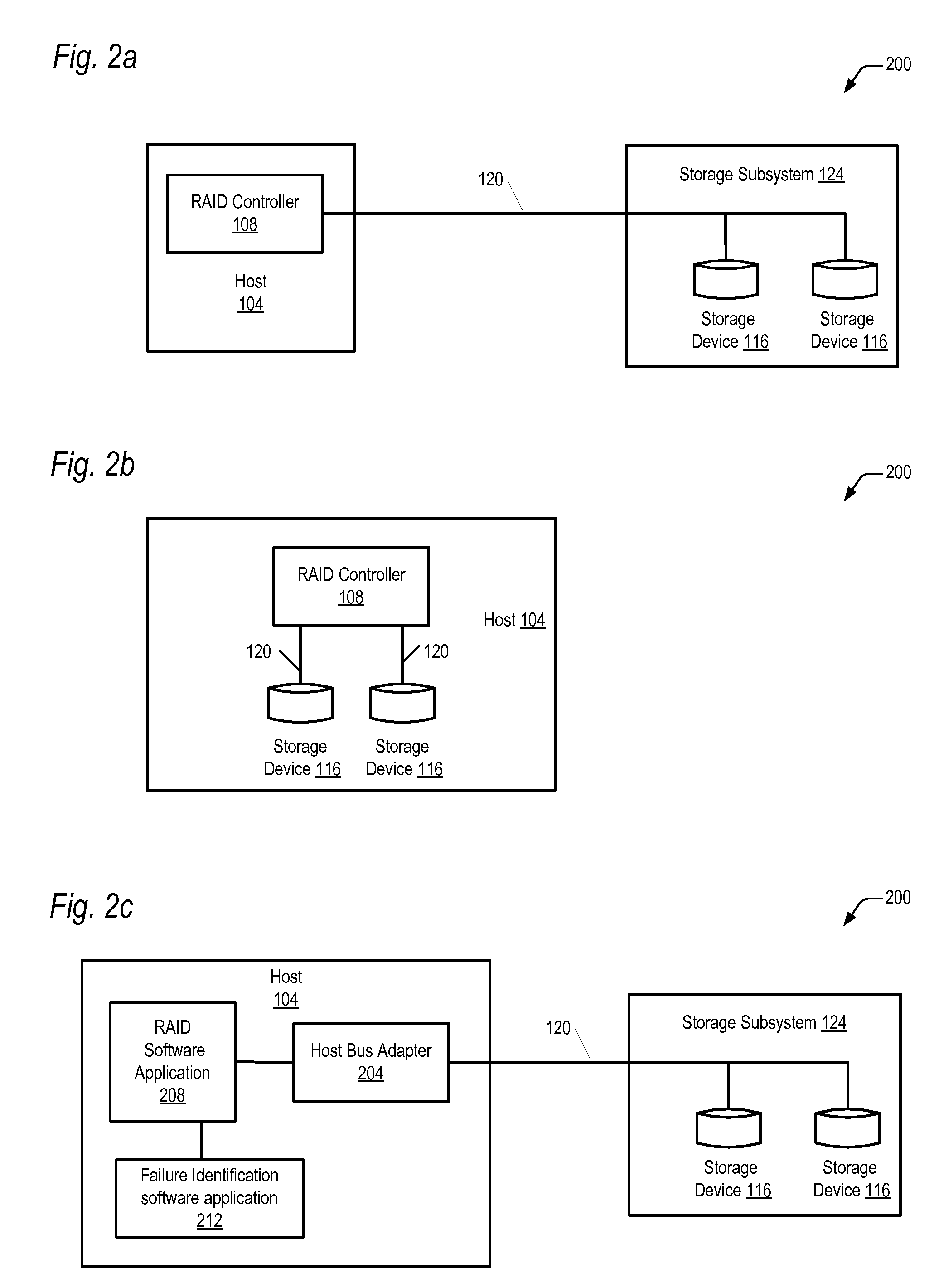
Apparatus and method for identifying disk drives with unreported data corruption
InactiveUS20090259882A1No great storage burdenSave cost and storage spaceRedundant operation error correctionMemory systemsRAIDData Corruption
A RAID controller uses a method to identify a storage device of a redundant array of storage devices that is returning corrupt data to the RAID controller. The method includes reading data from a location of each storage device in the redundant array a first time, and detecting that at least one storage device returned corrupt data. In response to detecting corrupt data, steps are performed for each storage device in the redundant array. The steps include reading data from the location of the storage device a second time without writing to the location in between the first and second reads, comparing the data read the first and second times, and identifying the storage device as a failing storage device if the compared data has a miscompare. Finally, the method includes updating the location of each storage device to a new location and repeating the steps for the new location.
Owner:DOT HILL SYST
Apparatus and method for secure hash algorithm
ActiveUS20050089160A1Performed quicklyIncrease probabilityUser identity/authority verificationUnauthorized memory use protectionSecure Hash AlgorithmOpcode
The present invention provides an apparatus and method for performing hash operations. The apparatus provides an instruction for employment by a device. The instruction directs the device to perform a hash operation. The instruction has an opcode field and a repeat prefix field. The opcode field prescribes that the device accomplish the hash operation. The repeat prefix field is coupled to the opcode field and indicates that the hash operation prescribed by the instruction is to be accomplished on one or more message blocks.
Owner:VIA TECH INC
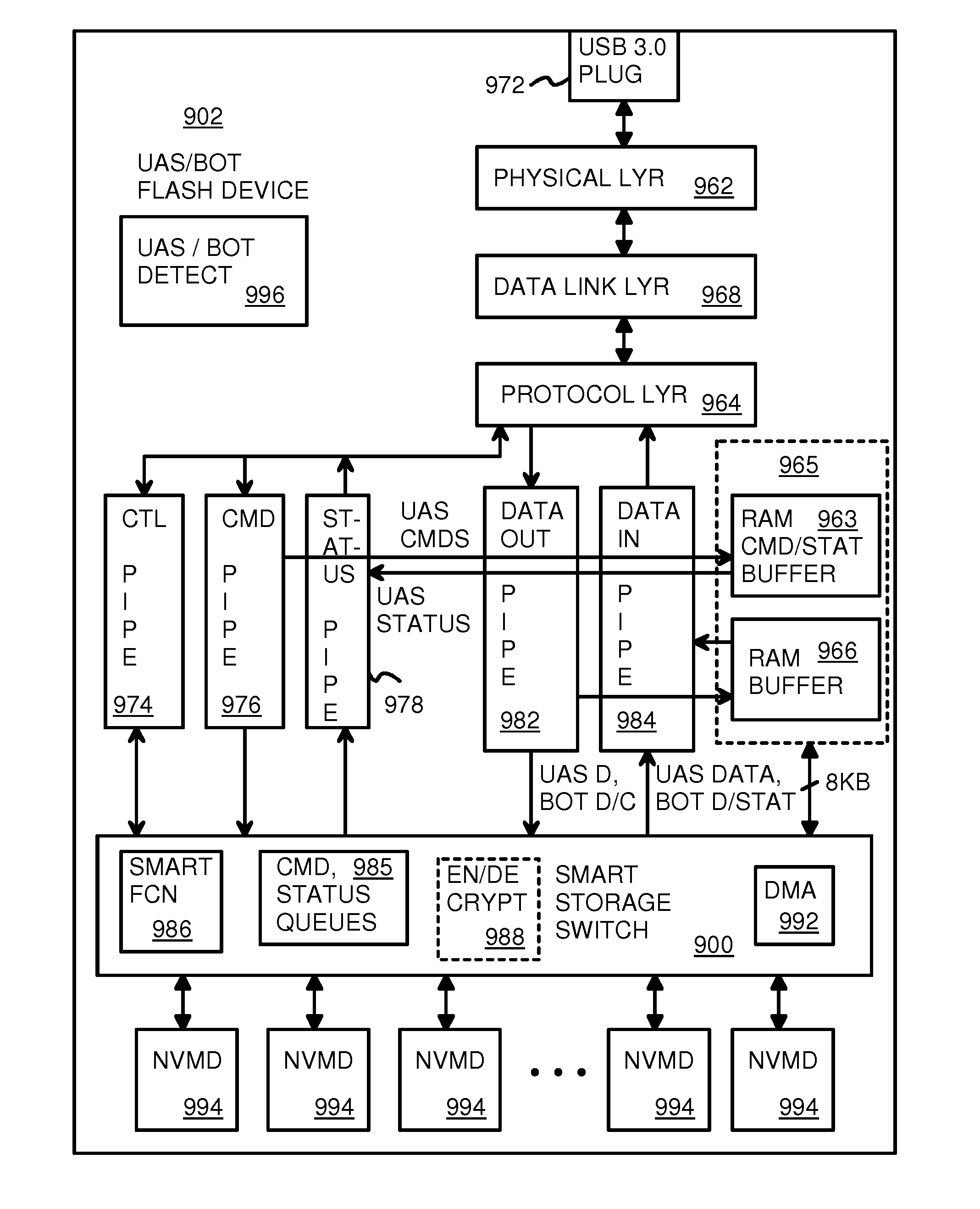
USB-attached-SCSI flash-memory system with additional command, status, and control pipes to a smart-storage switch
InactiveUS8180931B2Performed quicklyDouble access speedRead-only memoriesDigital storageSCSINetwork packet
An electronic flash-memory card has additional pipes for commands and status messages so that data pipes are not clogged with commands and status messages, allowing for a higher data throughput. The command and status pipes are activated when a UAS / BOT detector detects that a host is using a USB-Attached-SCSI (UAS) mode rather than a Bulk-Only-Transfer (BOT) mode. The host can send additional commands and data without waiting for completion of a prior command when operating in UAS mode but not while operating in BOT mode. A command queue (CQ) in the device re-orders commands for accessing flash memory and merges data in a RAM buffer. Smaller 1 KB USB packets in the data pipes are merged into larger 8 KB payloads in the RAM buffer, allowing for more efficient flash access.
Owner:SUPER TALENT TECH CORP
Method and apparatus for quantitative microimaging
InactiveUS20120224053A1Easy to operateSimple designMaterial analysis by optical meansLaboratory glasswaresQuantitative determinationAnalytical chemistry
Owner:BOARD OF RGT THE UNIV OF TEXAS SYST +1
Living body guidance control method for a biometrics authentication device, and biometrics authentication device
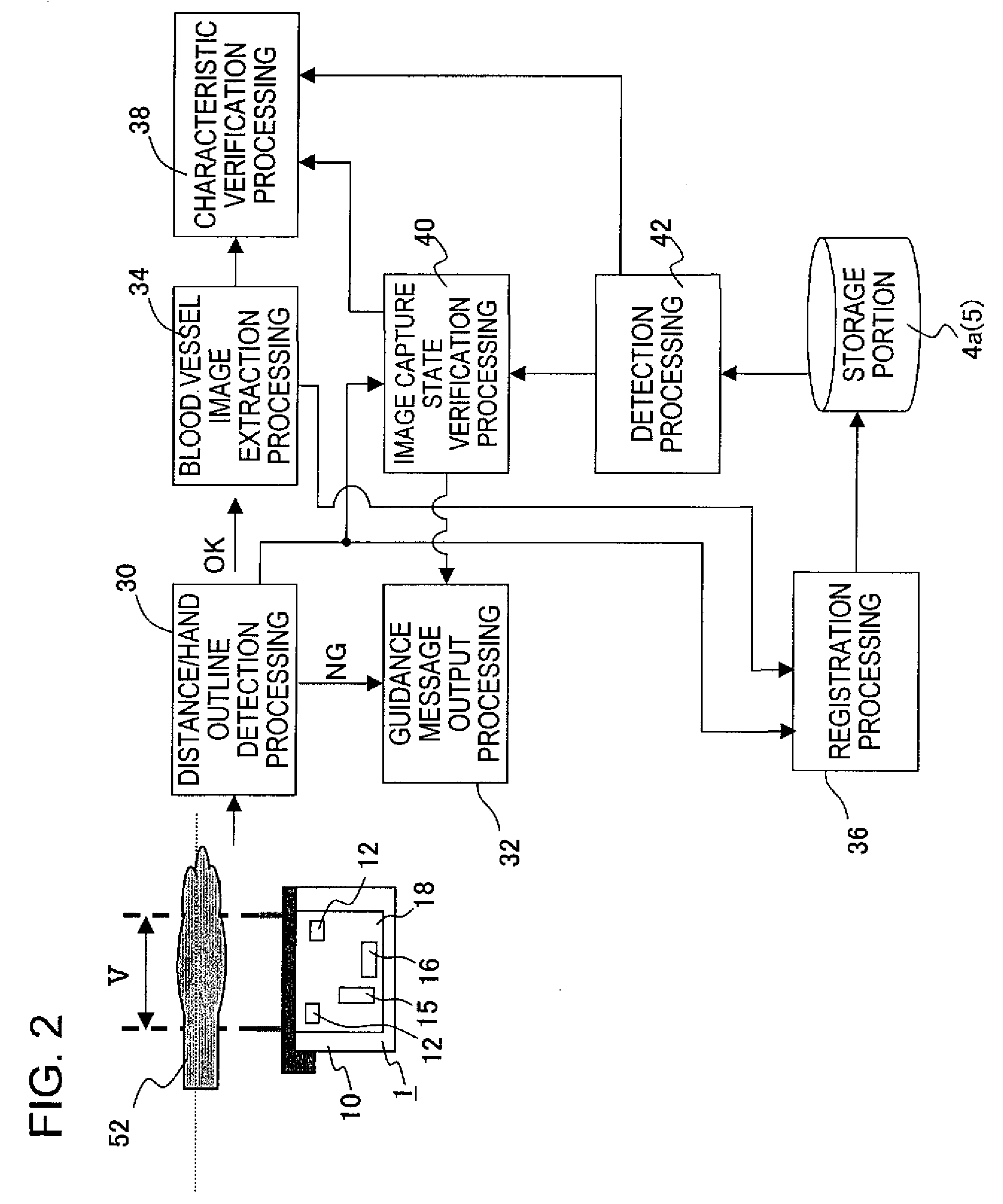
ActiveUS20080226136A1Improve reliabilityShorten the timePerson identificationImage data processing detailsComputer hardwareBiological body
A biometrics authentication device identifies characteristics of the body from captured images of the body and performs individual authentication. The device guides a user, at the time of verification, to the image capture state at the time of registration of biometrics characteristic data. At the time of registration of biometrics characteristic data, body image capture state data is extracted from an image captured by an image capture unit and is registered in a storage unit, and at the time of verification the registered image capture state data is read from the storage unit and is compared with image capture state data extracted at the time of verification, and guidance of the body is provided. Alternatively, an outline of the body at the time of registration, taken from image capture state data at the time of registration, is displayed.
Owner:FUJITSU LTD +1
USB-Attached-SCSI Flash-Memory System with Additional Command, Status, and Control Pipes to a Smart-Storage Switch
InactiveUS20100122021A1Addressing slow performancePerformed quicklyMemory adressing/allocation/relocationRead-only memoriesSCSINetwork packet
An electronic flash-memory card has additional pipes for commands and status messages so that data pipes are not clogged with commands and status messages, allowing for a higher data throughput. The command and status pipes are activated when a UAS / BOT detector detects that a host is using a USB-Attached-SCSI (UAS) mode rather than a Bulk-Only-Transfer (BOT) mode. The host can send additional commands and data without waiting for completion of a prior command when operating in UAS mode but not while operating in BOT mode. A command queue (CQ) in the device re-orders commands for accessing flash memory and merges data in a RAM buffer. Smaller 1 KB USB packets in the data pipes are merged into larger 8 KB payloads in the RAM buffer, allowing for more efficient flash access.
Owner:SUPER TALENT TECH CORP
Apparatus and method for motion estimation and image processing apparatus
InactiveUS20110200107A1Perform quicklyPerformed quicklyColor television with pulse code modulationColor television with bandwidth reductionMotion vectorImage processing
A motion estimation apparatus and method for quickly performing video encoding based on a user input through a user input device are provided. The motion estimation apparatus includes an input receiver for receiving a user input, an input pattern analysis unit for analyzing the received user input and determining a user input pattern according to the analyzed user input, a storage for storing history information of a motion vector according to the user input pattern, and a motion estimator for initially estimating a motion vector of a motion estimation block of a current frame with reference to history information of a motion vector corresponding to the user input pattern stored in the storage, deciding a search location of a block matching the motion estimation block from a reference frame, and performing motion estimation on the motion estimation block using the decided search location.
Owner:SAMSUNG ELECTRONICS CO LTD
Secondary index search
InactiveUS6266660B1Reduce in quantityAddressing slow performanceData processing applicationsDigital data processing detailsRelational databaseSelection criterion
A secondary index search in a relational database system compares primary key selection criteria against a primary key value stored in a secondary index record that satisfies secondary key selection criteria instead of searching a primary index for a primary key value that satisfies the primary key selection criteria.
Owner:UNISYS CORP
Method and apparatus for video encoding
InactiveUS20050190977A1Performed quicklyReduce signal to noise ratioCharacter and pattern recognitionPaving detailsComputer graphics (images)Video encoding
Provided are a method and apparatus for video encoding, in which an encoding mode is rapidly decided and video encoding is performed in the decided encoding mode. The method for video encoding includes determining whether a predetermined block of a predetermined size forming a video satisfies predetermined conditions corresponding to a first mode that is included in a plurality of encoding modes used to encode the video and choosing the first mode as an encoding mode of the predetermined block if the predetermined conditions are satisfied.
Owner:SUNGKYUNKWAN UNIVERSITY +1
Memory device with programmable receivers to improve performance
InactiveUS20050108468A1Easy to doReduce simultaneous switching noiseMemory loss protectionDigital storageEngineeringElectrical and Electronics engineering
A memory system having a plurality of DRAMs which are selectively provided non-inverted or inverted signals. The DRAMs have the ability to accept non-inverted or inverted address / command signals from a register that drives a plurality of signals simultaneously. The system includes DRAM receivers with programmable input polarity and a register with programmable output polarity.
Owner:MARVELL ASIA PTE LTD
Method and apparatus for constructing synchronous sensor network
ActiveUS20100118737A1Increase lifeShorten initialization timeEnergy efficient ICTNetwork traffic/resource managementNetwork mediaData channel
Provided are a method and apparatus for using a synchronous sensor network medium access control (MAC) protocol such as a ZigBee or IEEE 802.15.4 low-rate wireless personal area network (WPAN). Also provided are a method and apparatus for constructing a ubiquitous sensor network (USN) of which a life is increased by using power beacons and reducing the number of unnecessary control packets (beacon packets), thereby reducing an initialization time between nodes and preventing beacon collision. According to the present invention, a beacon packet channel having a large output power and a data channel of which a transmission range is restricted by reducing an output power to be less than that of the beacon packet channel, may be simultaneously used.
Owner:ELECTRONICS & TELECOMM RES INST
Methods and Apparatus for Modeling Electromagnetic Scattering Properties of Microscopic Structures and Methods and Apparatus for Reconstruction of Microscopic Structures
ActiveUS20110218789A1Addressing slow performancePerformed quicklyAnalogue computers for electric apparatusPhotomechanical apparatusElectric fluxMicrostructure
Improved convergence in the volume-integral method (VIM) of calculating electromagnetic scattering properties of a structure is achieved by numerically solving a volume integral equation for a vector field, F, rather than the electric field, E. The vector field, F, may be related to the electric field, E, by a change of basis, and may be continuous at material boundaries where the electric field, E, has discontinuities. Convolutions of the vector field, F, are performed using convolution operators according the finite Laurent rule (that operate according to a finite discrete convolution), which allow for efficient matrix-vector products via 1D and / or 2D FFTs (Fast Fourier Transforms). An invertible convolution-and-change-of-basis operator, C, is configured to transform the vector field, F, to the electric field, E, by performing a change of basis according to material and geometric properties of the periodic structure. After solving the volume integral for the vector field, F, an additional post-processing step may be used to obtain the electric field, E, from the vector field, F. The vector field, F, may be constructed from a combination of field components of the electric field, E, and the electric flux density, D, by using a normal-vector field, n, to filter out continuous components.
Owner:ASML NETHERLANDS BV
Processor reduction unit for accumulation of multiple operands with or without saturation
ActiveUS20050071413A1Performed quicklyEasily pipelinedDigital computer detailsConcurrent instruction executionCombined useOperand
A processor having a reduction unit that sums m input operands plus an accumulator value, with the option of saturating after each addition or wrapping around the result of each addition. The reduction unit also allows the m input operands to be subtracted from the accumulator value by simply inverting the bits of the input operands and setting a carry into each of a plurality of reduction adders to one. The reduction unit can be used in conjunction with m parallel multipliers to quickly perform dot products and other vector operations with either saturating or wrap-around arithmetic.
Owner:QUALCOMM INC
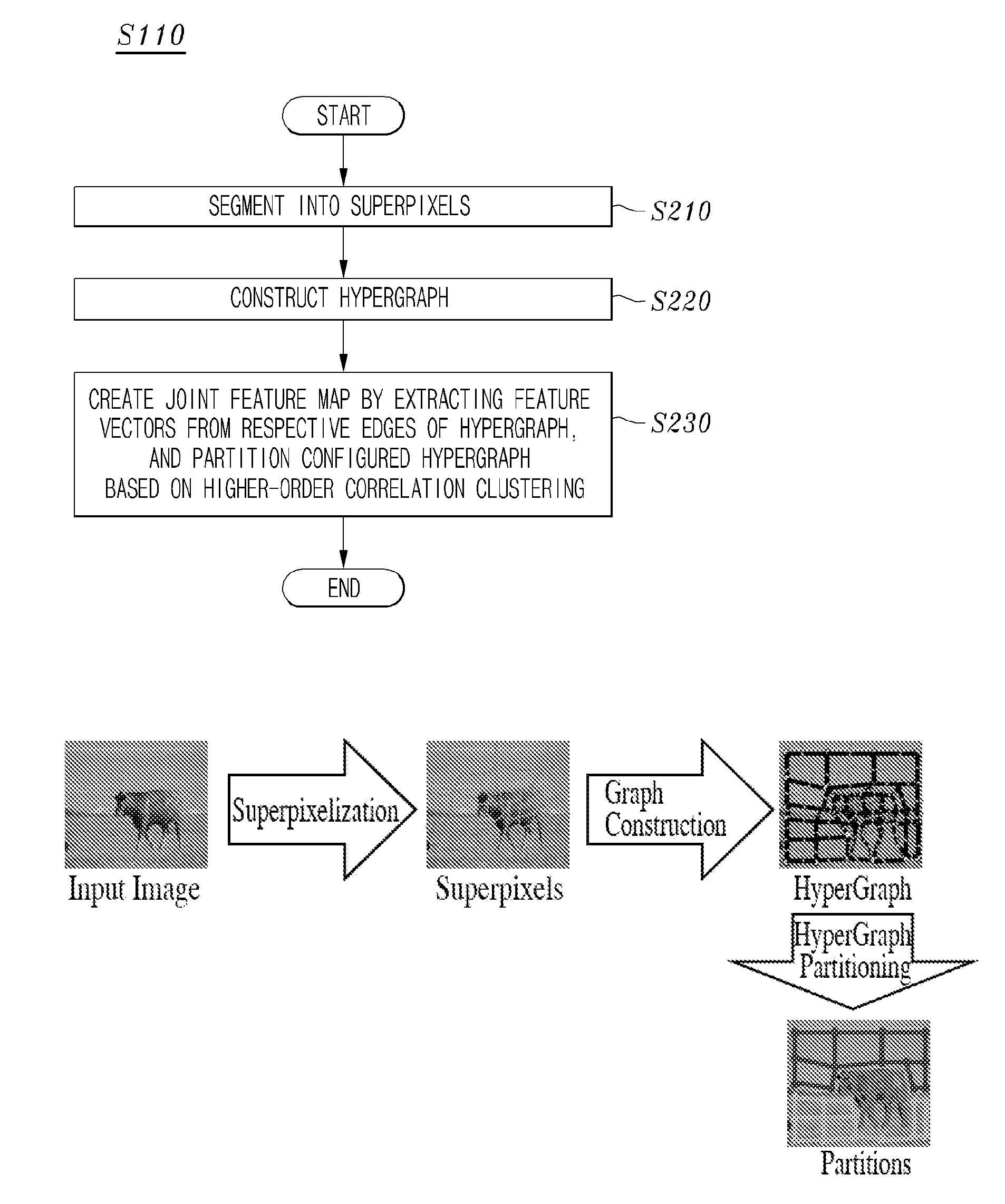
Image segmentation method using higher-order clustering, system for processing the same and recording medium for storing the same
ActiveUS20130188869A1Improve accuracyAddressing slow performanceImage analysisCharacter and pattern recognitionFeature vectorHypergraph
Disclosed herein is a method of processing images based on image segmentation using higher-order correlation clustering. In an image segmentation method according to an embodiment of the present invention, an input image is segmented into superpixels. A hypergraph is constructed by connecting two or more adjacent superpixels, among the superpixels, to one another. A joint feature map is created by extracting feature vectors from respective edges of the hypergraph, and partitioning the hypergraph based on higher-order correlation clustering in consideration of specific constraints.
Owner:KOREA ADVANCED INST OF SCI & TECH
Processor reduction unit for accumulation of multiple operands with or without saturation
ActiveUS7593978B2Performed quicklyEasily pipelinedDigital computer detailsConcurrent instruction executionOperandWrap around
A processor having a reduction unit that sums m input operands plus an accumulator value, with the option of saturating after each addition or wrapping around the result of each addition. The reduction unit also allows the m input operands to be subtracted from the accumulator value by simply inverting the bits of the input operands and setting a carry into each of a plurality of reduction adders to one. The reduction unit can be used in conjunction with m parallel multipliers to quickly perform dot products and other vector operations with either saturating or wrap-around arithmetic.
Owner:QUALCOMM INC
Device and method for testing a tire, in particular by means of an interferometric measuring method
A device for testing a tire with two sidewalls and a tread portion in particular by means of an interferometric measuring method, is provided with a measuring unit with which the tire can be scanned to generate a measurement result, and with a positioning means for the measuring unit. The measuring unit comprises at least three measuring heads. The first measuring head and the second measuring head are used to scan the outer surface of the sidewalls, whereas the third measuring head is used to scan the inner surface of at least the tread portion. The device enables a tire to be fully tested quickly.
Owner:MAHNER BERNWARD +1
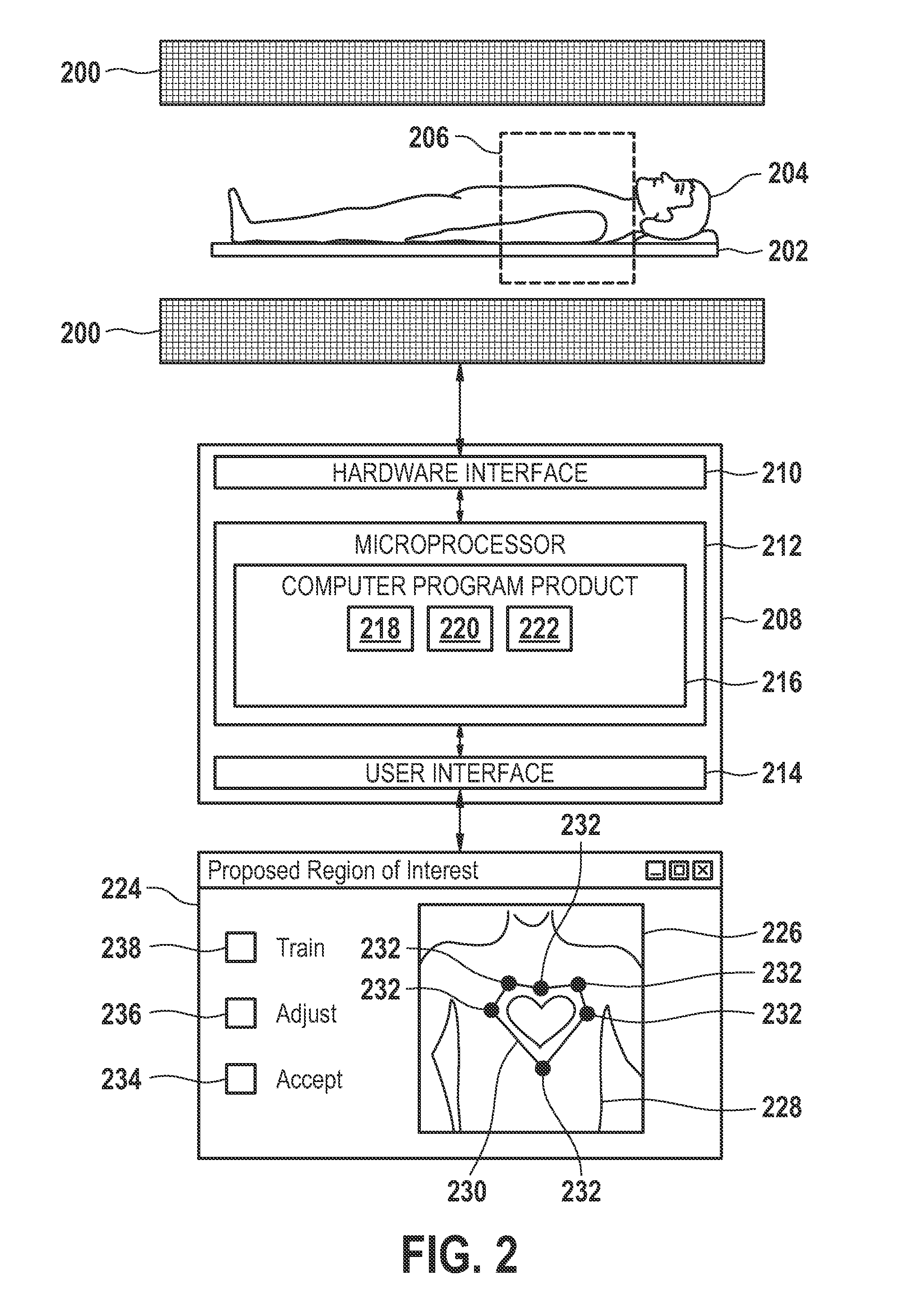
Method, apparatus, and computer program product for acquiring medical image data
InactiveUS20110229005A1Performed quicklyAddressing slow performanceImage enhancementImage analysisRegion of interestComputer program
A method of acquiring medical image data with at least one region of interest with a predefined freely shaped geometry comprising the following steps: acquiring a first set of medical image data, identifying at least one anatomical landmark in the first set of image data, determining the at least one region of interest with a trained pattern recognition module using the at least one anatomical landmark.
Owner:KONINKLIJKE PHILIPS ELECTRONICS NV
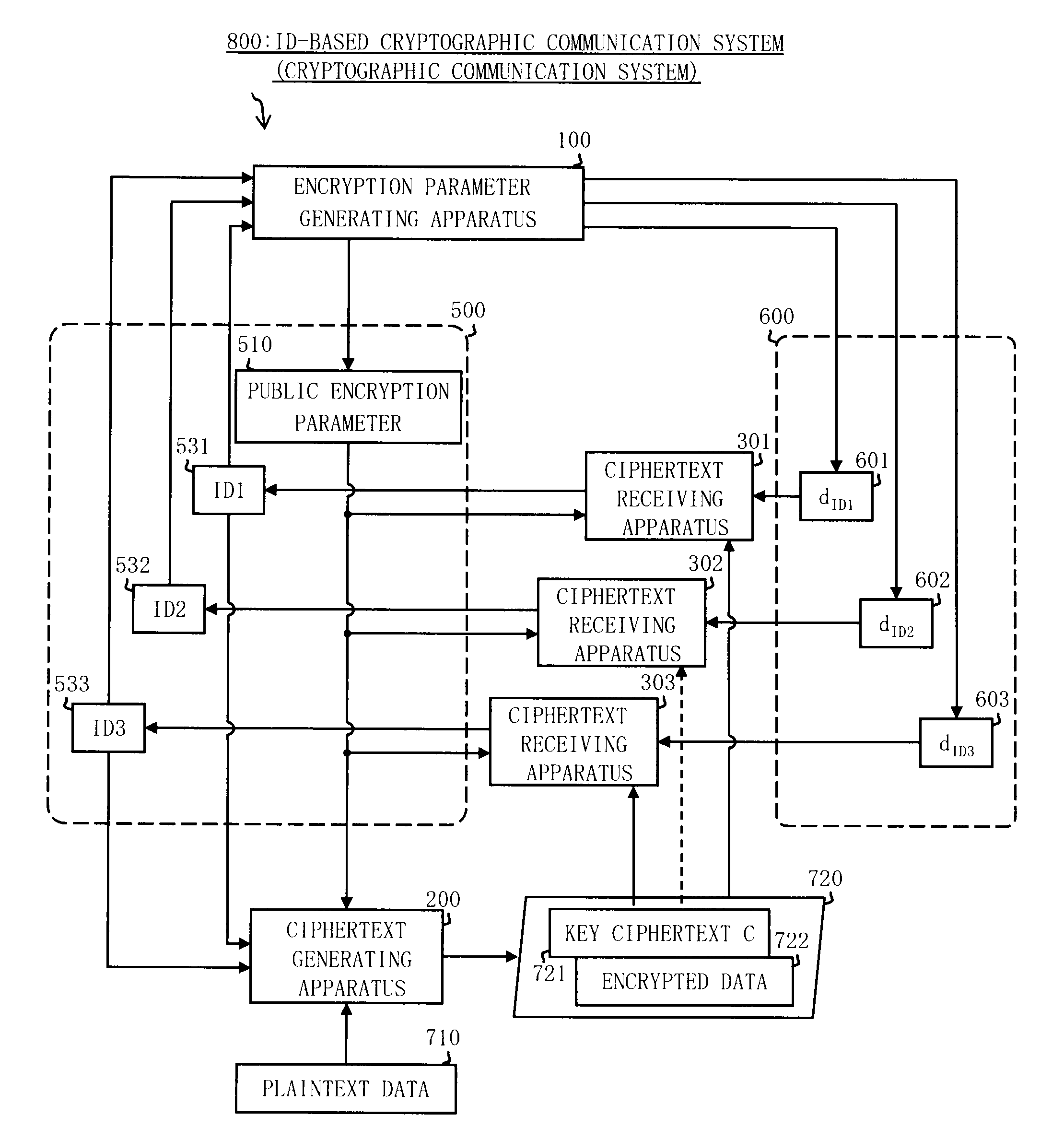
Ciphertext generating apparatus, cryptographic communication system, and group parameter generating apparatus
InactiveUS20100104094A1High speed encryption processingImprove processing efficiencyUser identity/authority verificationSecret communicationPlaintextCommunications system
The random number generating unit 222 randomly generates an integer s. The first ciphertext generating unit 241 generates a first ciphertext C1 by encrypting the plaintext M, based on the integer s. The second ciphertext generating unit 242 generates a second ciphertext C2i based on the integer s and a recipient ID. The third ciphertext generating unit 243 generates a third ciphertext C3i based on the integer s. The hash value calculation unit 244 calculates a hash value H0 by combining the first ciphertext C1i the second ciphertext C2i and the third ciphertext C3. The fourth ciphertext generating unit 245 generates a fourth ciphertext C4, based on the hash value H0. The ciphertext combining unit 246 generates a ciphertext C by combining the first ciphertext C1i the second ciphertext C2i the third ciphertext C3i and the fourth ciphertext C4. Thus, it is possible to provide an ID-based public key cryptographic communication system being secure even when transmitting ciphertexts generated by encrypting the same plaintext to a plurality of recipients.
Owner:MITSUBISHI ELECTRIC CORP
Automatic sound field correcting device and computer program therefor
InactiveUS20050135631A1Performed quicklyReduce processing timePseudo-stereo systemsFrequency response correctionSignal processing circuitsFrequency characteristic
An automatic sound field correcting device executes a signal process to the plurality of audio signals on respective correspondent signal transmission paths, and outputs them to a plurality of correspondent speakers to correct sound characteristics on the respective signal transmission paths. Namely, a measurement signal is supplied to each signal transmission path, and a measurement sound corresponding to it is outputted from the speaker to a sound space. The outputted measurement sound is detected as a detecting signal. The frequency characteristic of the audio signal on each signal transmission path is corrected by an equalizer, and a gain value of the equalizer is determined by a correction amount determining unit. A frequency characteristics correction is performed predetermined times. At a first correction, the correction amount determining unit determines the correction amount by performing a frequency analysis, based on the detecting signal, i.e. base on the detecting signal corresponding to the measurement sound actually outputted to the sound space. On the contrary, at and after a second correction, the correction amount determining unit determines the correction amount based on the detecting signal or an output signal of the equalizer. Namely, at and after the second correction, the output signal of the equalizer is supplied to the correction amount determining unit in a signal processing circuit as the need arises, and the frequency characteristics correction is performed without actually outputting the measurement sound to the sound space.
Owner:ONKYO KK D B A ONKYO CORP
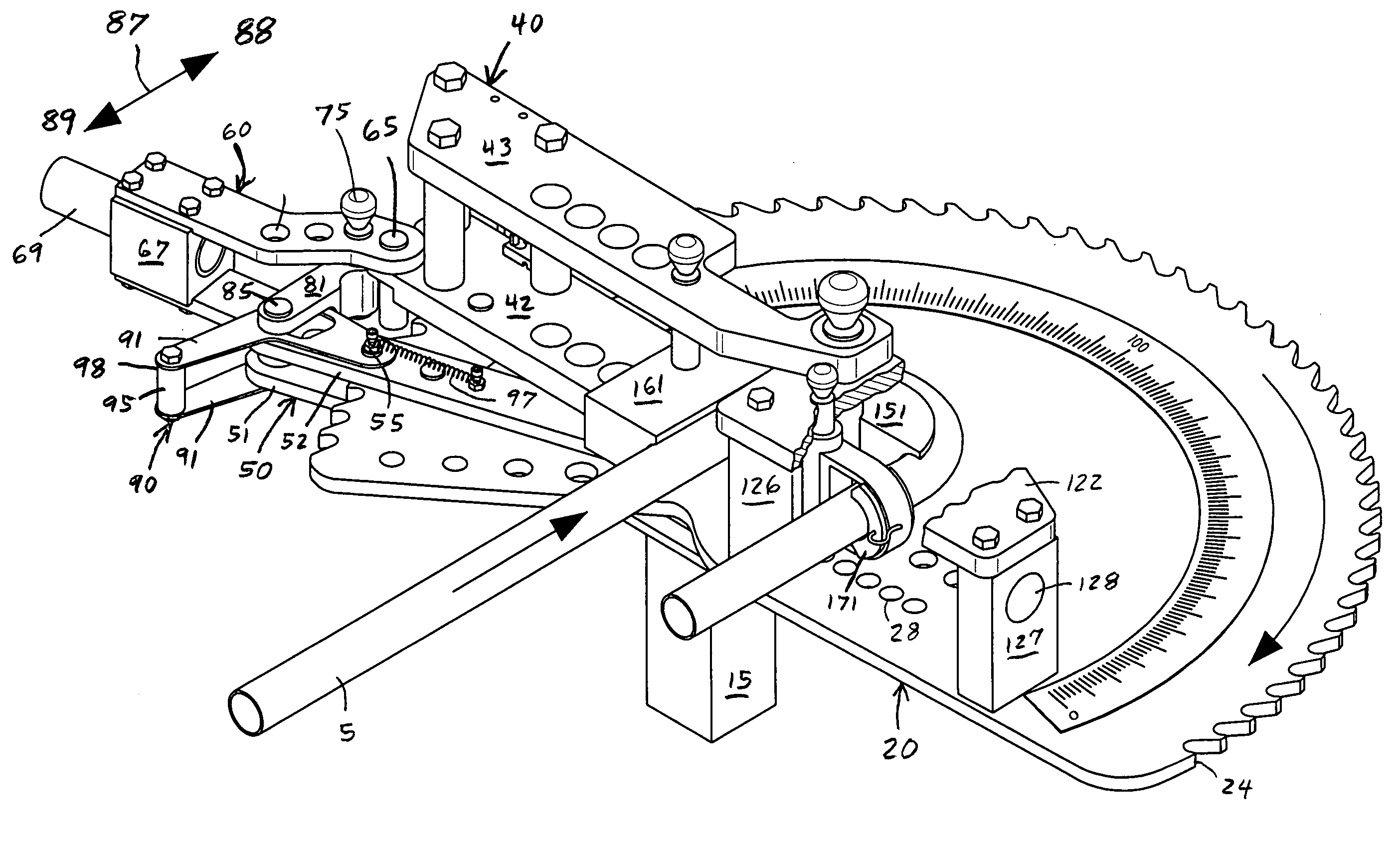
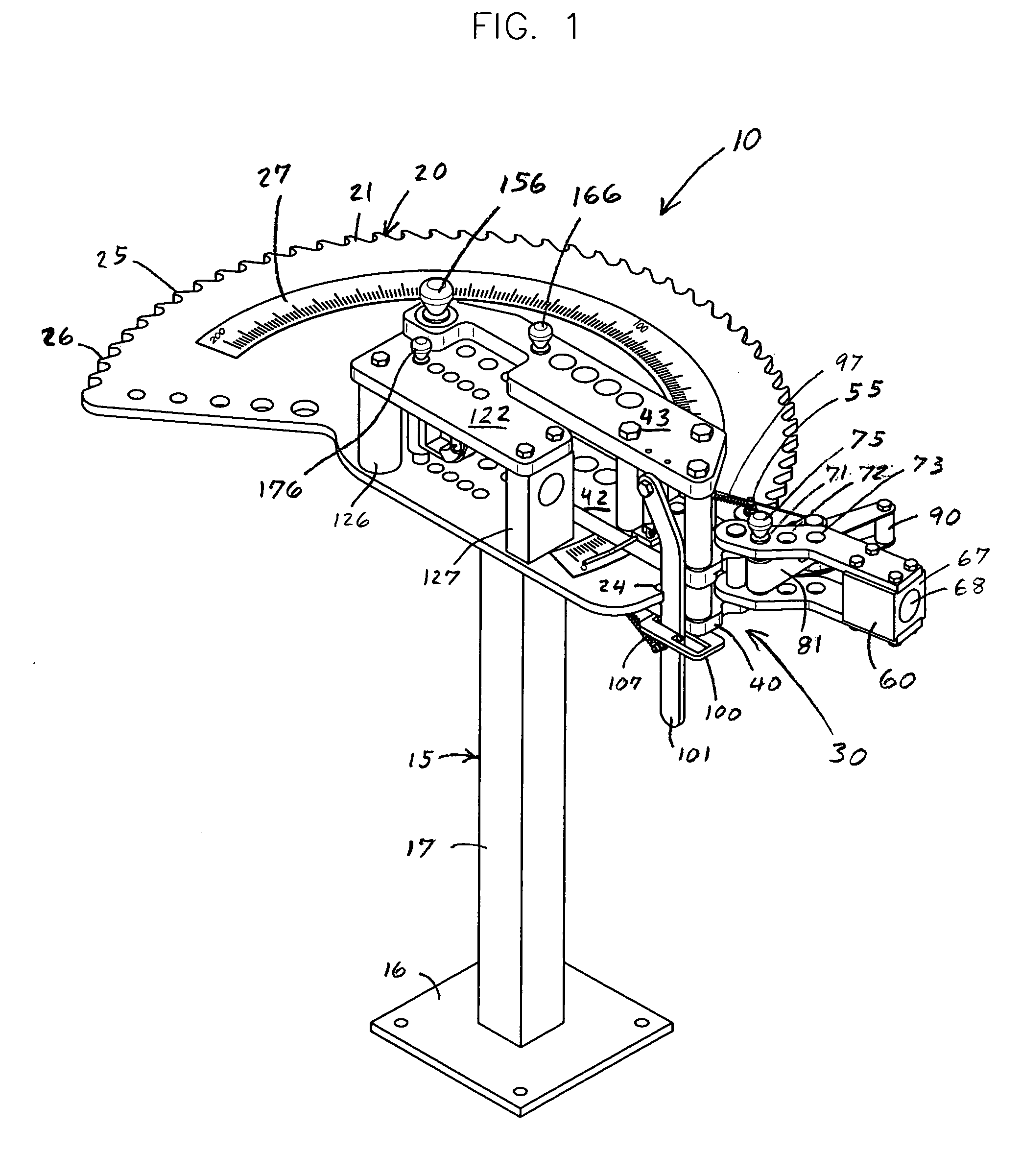
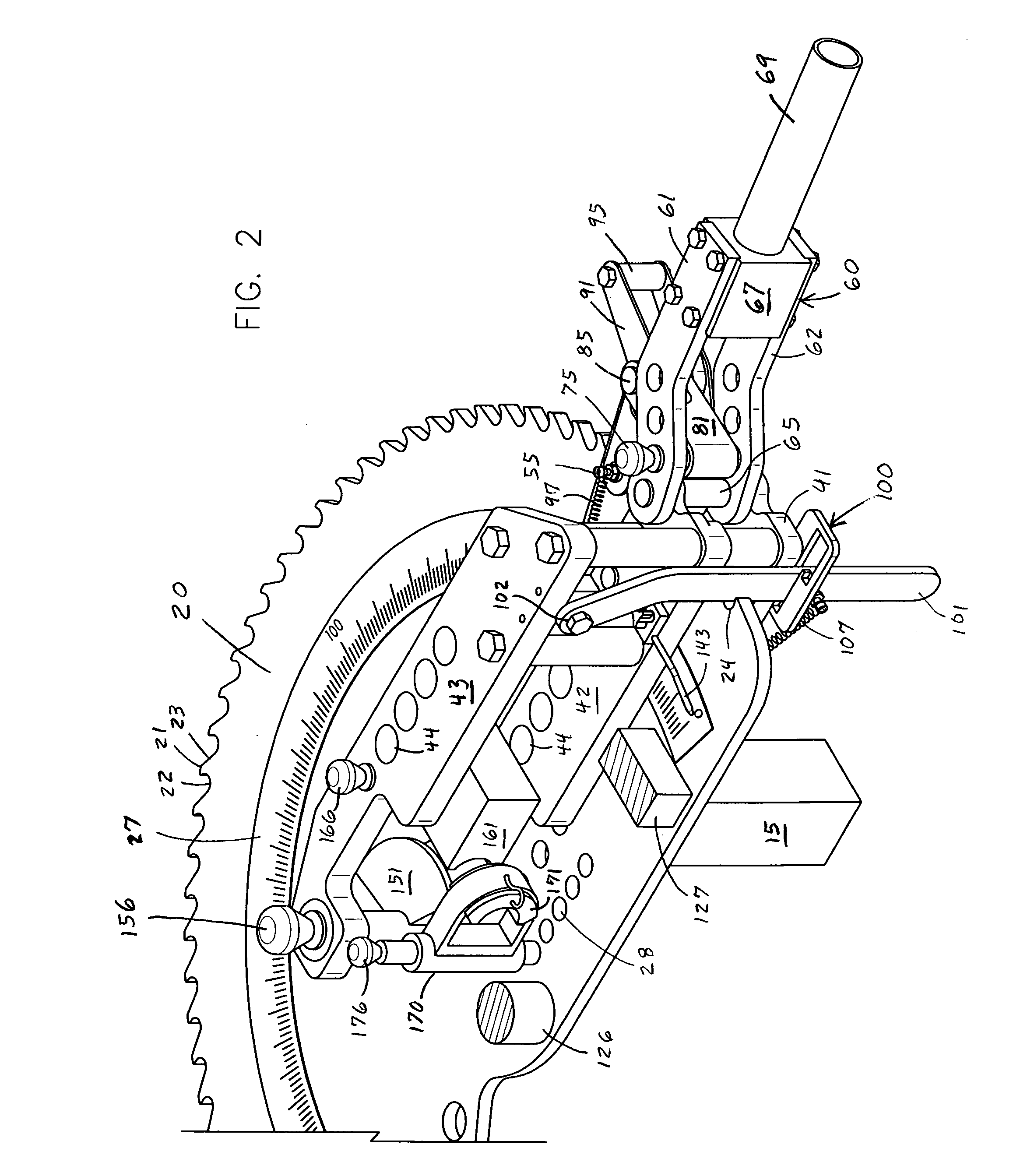
Tube bending machine
This invention is a manually operated tube bending machine with a power drive mechanism that is adjustably set to a desired bend speed. The bending machine includes a bending die, a counter die and a rotating hook die to form a desired bend into a tube or pipe. The tube bender includes a drive wheel with ratchet teeth around its perimeter. A drive pin grips one of the ratchet teeth. The drive pin is secured to a lever and torque bar. During each bending stroke, the lever and torque bar incrementally rotate the drive wheel a desired amount. The rotation of the drive wheel and hook die draw the tube through the bending and counter dies to bend the tube. An anti-spring back mechanism holds the position of the drive wheel while the power drive mechanism is advanced to grip the next ratchet tooth of the drive wheel.
Owner:JPW IND
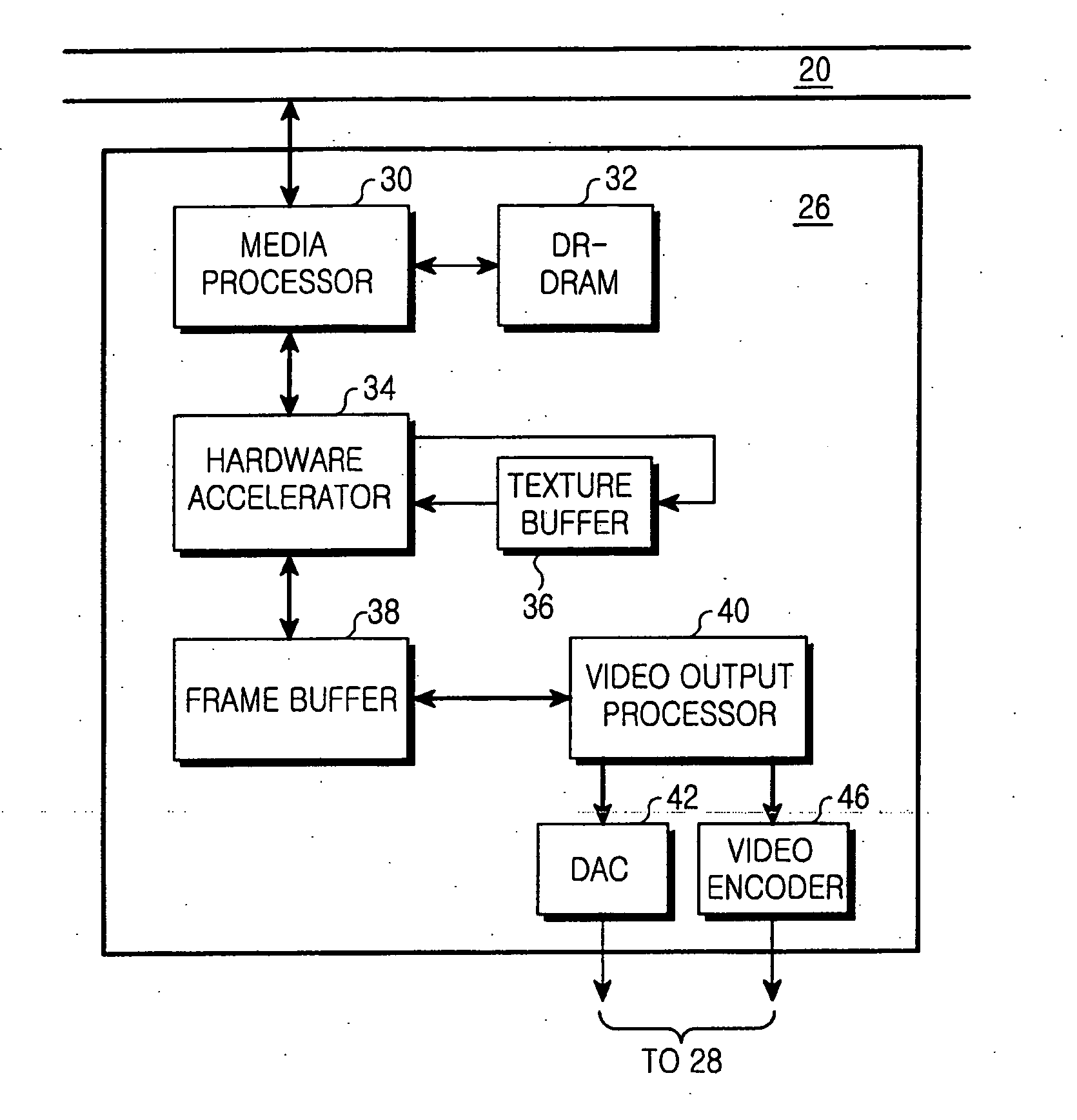
Graphics system and memory device for three-dimensional graphics acceleration and method for three dimensional graphics processing
InactiveUS20060098021A1Addressing slow performancePerformed quicklyMemory adressing/allocation/relocationImage memory managementGraphic systemTerm memory
A graphics system and a memory device for three-dimensional (3D) graphics acceleration, and a method for 3D graphics processing, are provided. In a memory device in a graphics system for 3D graphics processing, a memory structure includes a first memory area allocated to a texture buffer for storing texture data, and a second memory area allocated to a frame buffer for storing frame data in pixels. A comparator controls the memory structure to operate as the texture buffer if an input address to the memory structure indicates the first memory area and controls the memory structure to operate as the frame buffer if the input address indicates the second memory area. If the memory structure operates as the frame buffer, an ALU performs depth comparison or alpha-blending on input frame data and frame data read from the frame buffer.
Owner:SAMSUNG ELECTRONICS CO LTD +1
Data recording and reproducing apparatus, method for recording and reproducing video data, disk drive unit, and control unit of data recording and reproducing apparatus
InactiveUS7050705B1Performed quicklyFunction increaseTelevision system detailsColor television signals processingData bufferMagnetic disks
A data recording and reproducing apparatus of the present invention may be constituted by a hard disk drive, which comprises a magnetic disk, an input buffer positioned on an input path, an output buffer positioned on an output path, and a controller located between the input and output buffers and the magnetic disk. The controller operates to store (record) input data in the input buffer and transfer (reproduce) output data from the output buffer simultaneously, in parallel with reading or writing of the magnetic disk.
Owner:IBM CORP
Control system for throttle valve actuating device
InactiveUS6848420B2Addressing slow performancePerformed quicklyElectrical controlMachines/enginesControl systemSpecific model
A control system for a throttle valve actuating device is disclosed. The throttle valve actuating device has a throttle valve of an internal combustion engine and an actuator for actuating the throttle valve. Model parameters of a controlled object model obtained by modeling the throttle valve actuating device is identified by an identifier. The model parameters includes a specific model parameter irrelevant to an input and an output of the controlled object model. An opening of the throttle valve is controlled to a target opening using the identified model parameters. It is determined that the throttle valve actuating device is abnormal when the value of the specific model parameter becomes greater than a predetermined value.
Owner:HONDA MOTOR CO LTD
Wavelength Multiplexed Matrix-Matrix Multiplier
ActiveUS20180107237A1Performed quicklyEfficient collectionComputing operations for multiplication/divisionDigital dataComputational physicsMatrix multiplier
Optical systems for performing matrix-matrix multiplication in real time utilizing spatially coherent input light and wavelength multiplexing.
Owner:FATHOM RADIANT PBC
System and method for low latency multi-functional pipeline with correlation logic and selectively activated/deactivated pipelined data processing engines
InactiveUS10572824B2Performed quicklyBig advantageDigital data information retrievalDigital computer detailsComputer hardwareComputer architecture
Owner:IP RESERVOIR
Living body guidance control method for a biometrics authentication device, and biometrics authentication device
ActiveUS8184866B2Performed quicklyIncrease speedPerson identificationComputer security arrangementsComputer hardwareBiological body
A biometrics authentication device identifies characteristics of the body from captured images of the body and performs individual authentication. The device guides a user, at the time of verification, to the image capture state at the time of registration of biometrics characteristic data. At the time of registration of biometrics characteristic data, body image capture state data is extracted from an image captured by an image capture unit and is registered in a storage unit, and at the time of verification the registered image capture state data is read from the storage unit and is compared with image capture state data extracted at the time of verification, and guidance of the body is provided. Alternatively, an outline of the body at the time of registration, taken from image capture state data at the time of registration, is displayed.
Owner:FUJITSU LTD +1
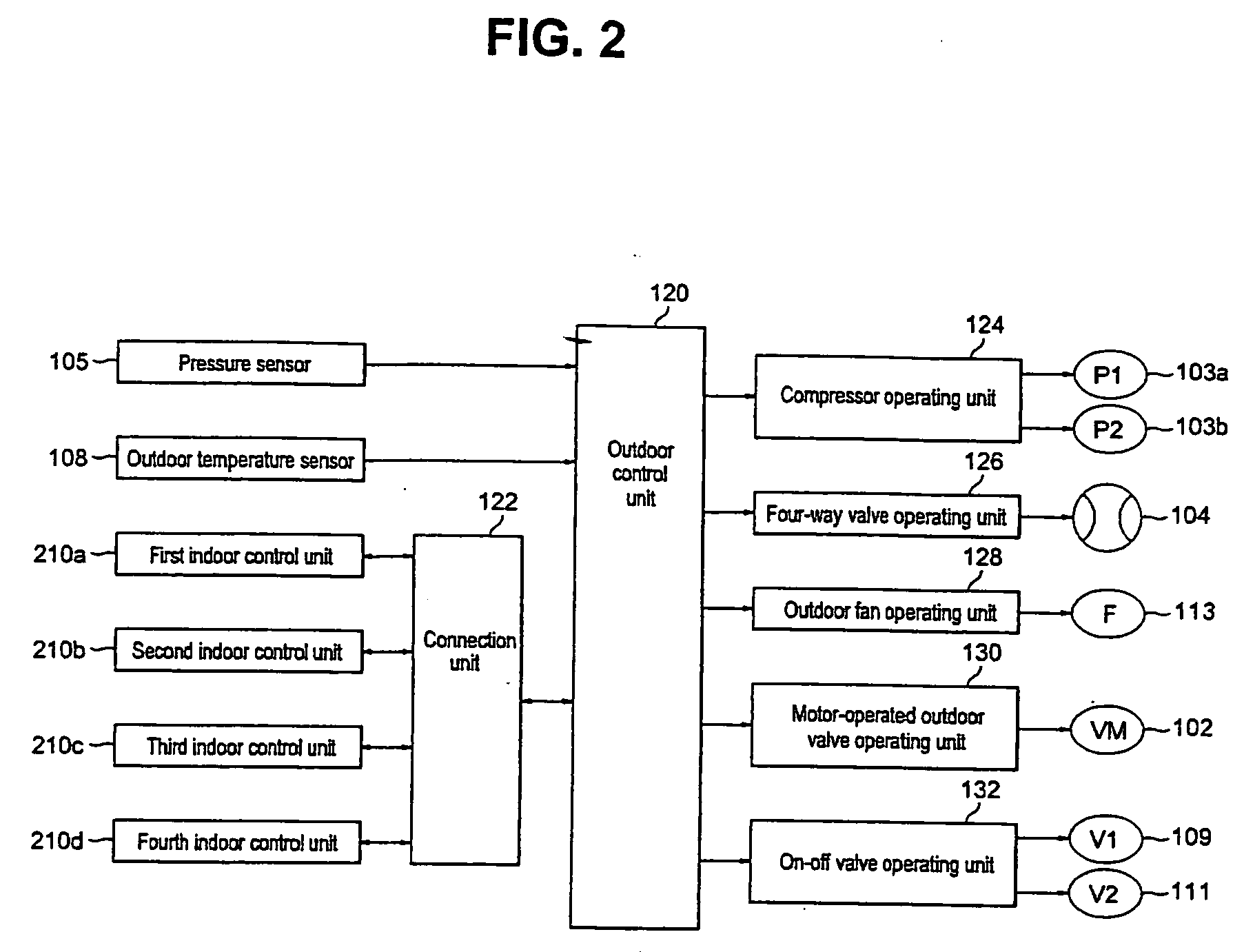
Air conditioning system and method for controlling the same
InactiveUS20050155361A1Performed quicklyOperation efficiency can be improvedTime-programme switchesCompression machines with non-reversible cycleEngineeringAir conditioning
An air conditioning system including an outdoor unit having at least one compressor, and at least one outdoor heat exchanger; a plurality of indoor units connected to the outdoor unit; a refrigerant guide unit to guide a refrigerant discharged from the at least one compressor to the indoor units through first and / or second routes; and a control unit to simultaneously control a first quantity of the refrigerant discharged from the at least one compressor to at least one of the indoor units operating in a cooling mode through the first route, and a second quantity of the refrigerant discharged from the at least one compressor to a remainder of the indoor units operating in a heating mode through the second route.
Owner:SAMSUNG ELECTRONICS CO LTD
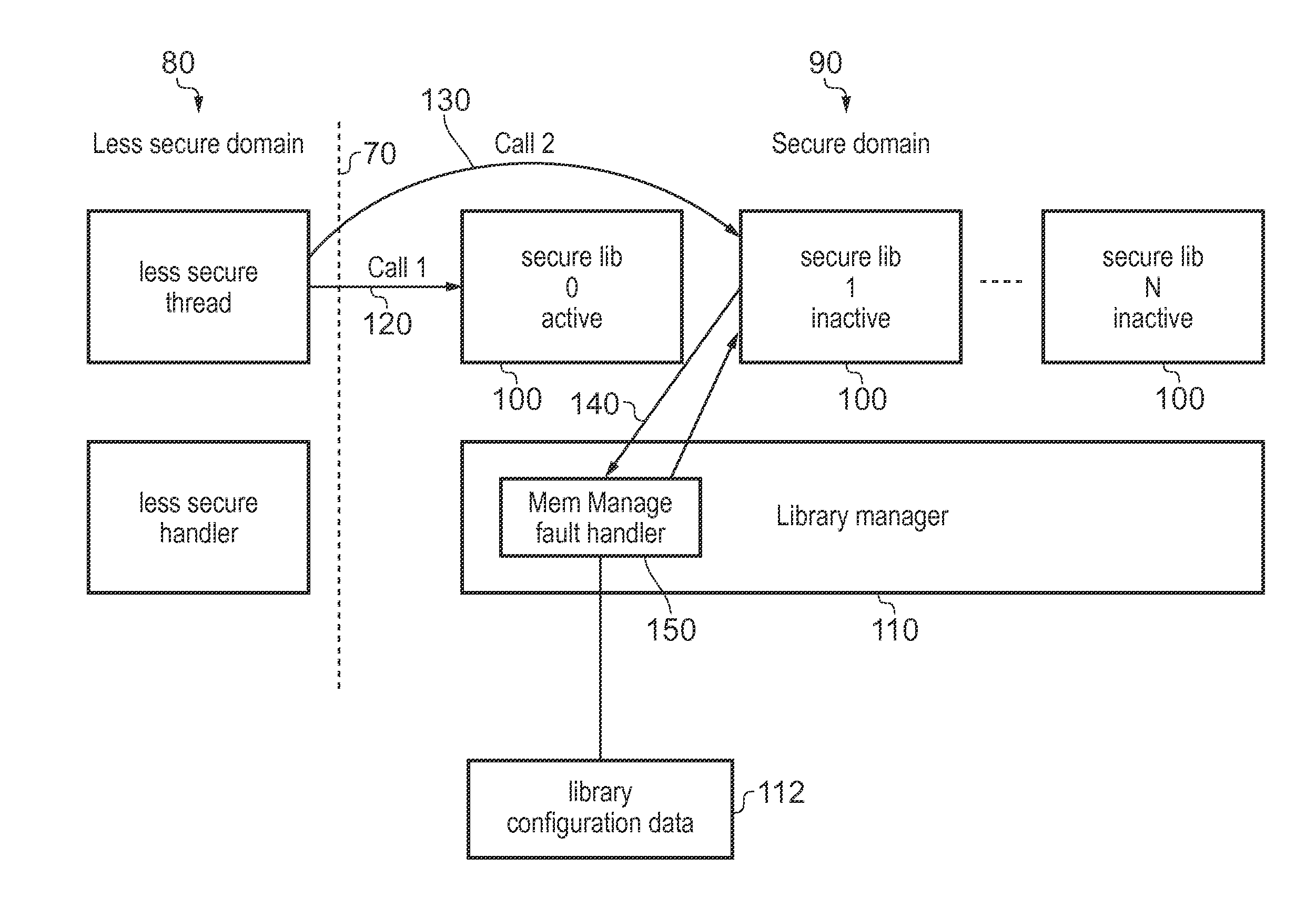
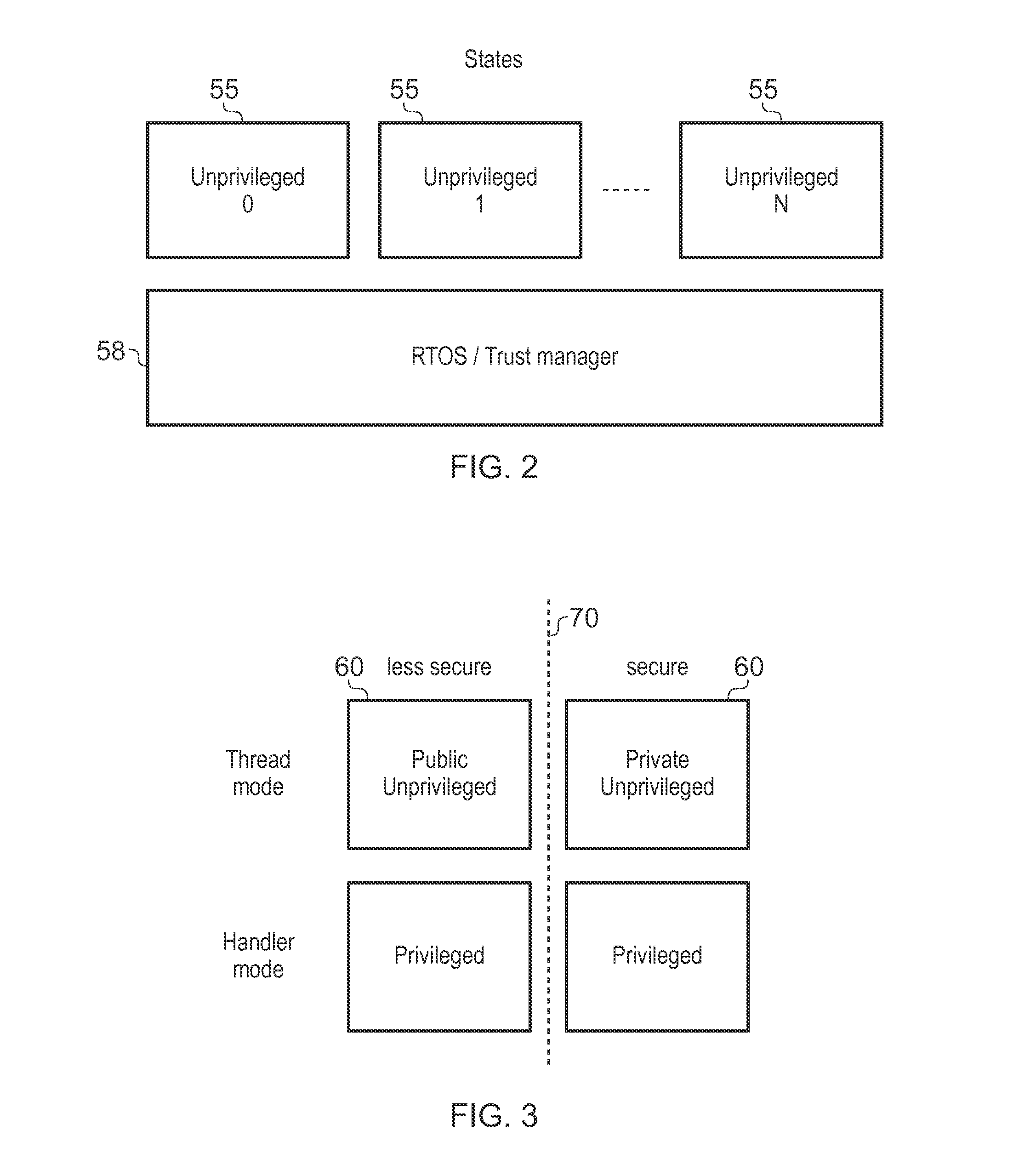
Security protection of software libraries in a data processing apparatus
ActiveUS20140373171A1Performed quicklyAvoid needDigital data processing detailsAnalogue secracy/subscription systemsLibrary managementSecurity check
A processing apparatus 2 has a secure domain 90 and a less secure domain 80. Security protection hardware 40 performs security checking operations when the processing circuitry 2 calls between domains. A data store 6 stores several software libraries 100 and library management software 110. The library management software 110 selects at least one of the libraries 100 as an active library which is executable by the processing circuitry 4 and at least one other library 100 as inactive libraries which are not executable. In response to an access to an inactive library, the library management software 110 switches which library is active.
Owner:ARM LTD
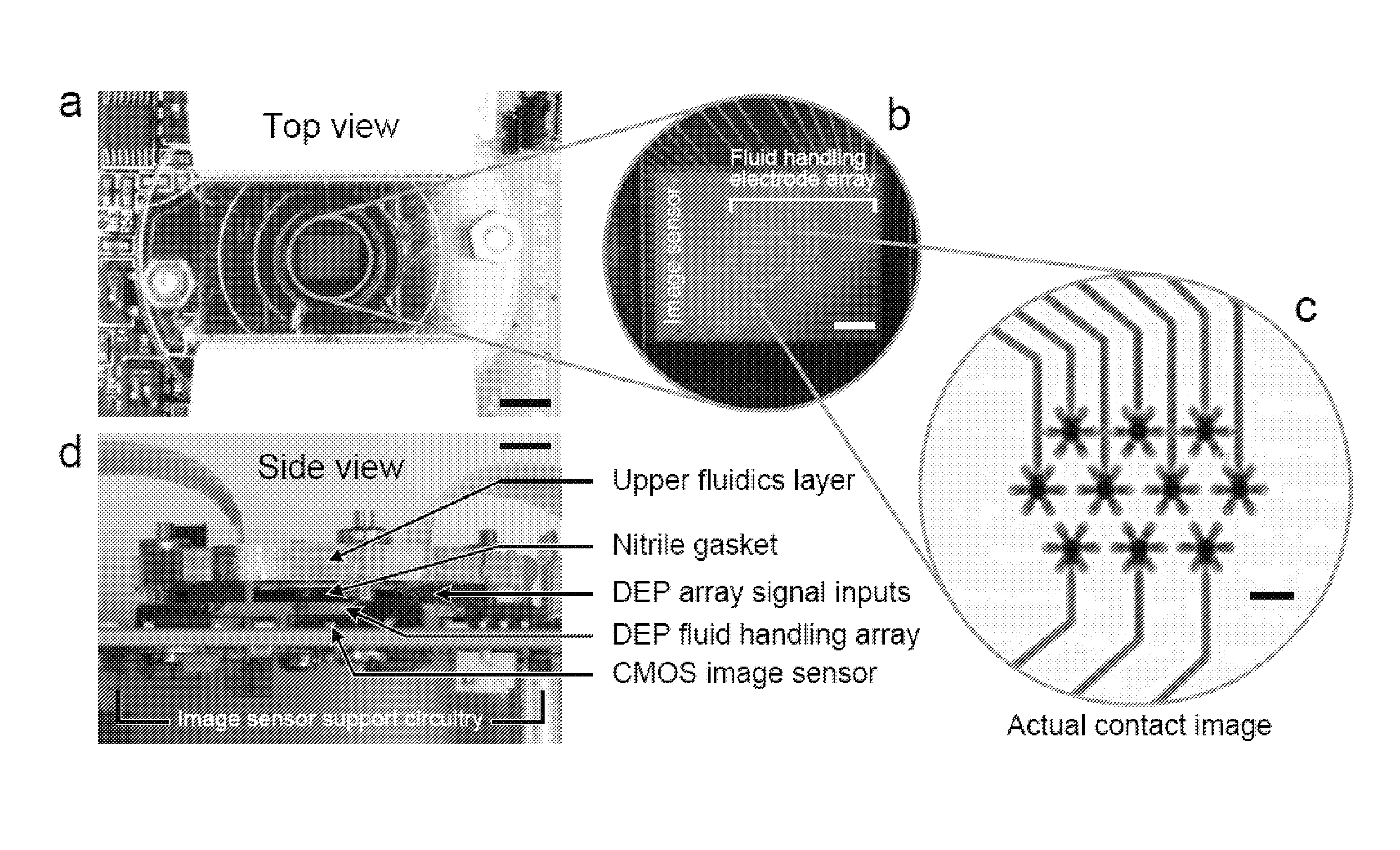
Cytological imaging systems and methods
InactiveUS20060077541A1Efficiently madePerformed quicklyImage enhancementImage analysisImage systemCytology sample
The present invention relates to the analysis of specimens. Specifically, the invention relates to methods and apparatus for reviewing specimen slides, including apparatus for holding the slides. The invention also relates to an automatic focusing method for an imaging system and methods for accommodating vibration in the imaging system. In particular, the methods and apparatus may be applied to the automated analysis of cytological specimen slides.
Owner:CYTYC CORP
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com