Patents
Literature
Hiro is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
38results about How to "Propagation delay" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
Enhanced copper posts for wafer level chip scale packaging
ActiveUS20080296764A1Increased shear strengthImprove conductivitySemiconductor/solid-state device detailsSolid-state devicesElectrical connectionCopper electrode
An enhanced wafer level chip scale packaging (WLCSP) copper electrode post is described having one or more pins that protrude from the top of the electrode post. When the solder ball is soldered onto the post, the pins are encapsulated within the solder material. The pins not only add shear strength to the soldered joint between the solder ball and the electrode post but also create a more reliable electrical connection due to the increased surface area between the electrode post / pin combination and the solder ball. Moreover, creating an irregularly shaped solder joint retards the propagation of cracks that may form in the intermetal compounds (IMC) layer formed at the solder joint.
Owner:ADVANCED MFG INNOVATIONS INC
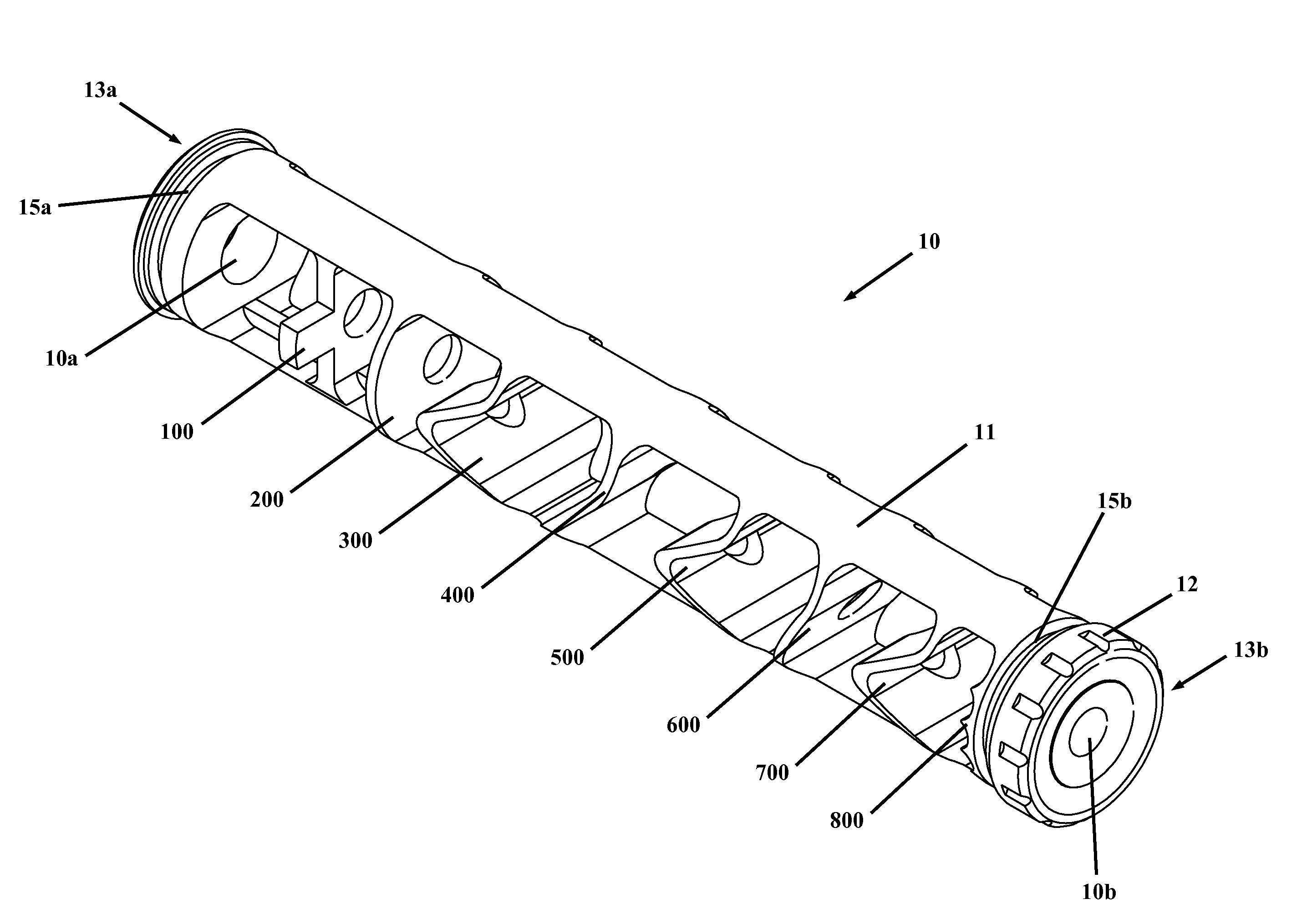
Monolithic firearm suppressor
A monolithic suppressor for suppressing sounds generated by the discharge of a firearm, wherein the discharge generates propellant gases. The monolithic suppressor includes a bore having a first end and a second end, the first end having an inlet aperture and the second end having an outlet aperture. In addition, a plurality of baffles are disposed within the bore, wherein the plurality of baffles further define a plurality of chambers. The chambers of the suppressor include at least an arcuate baffle and a slanted baffle. The plurality of chambers are configured to cause the propellant gases to spin in a plurality of vortices within one or more of the chambers thereby slowing the propagation of the gases within the suppressor.
Owner:TEMPLAR TACTICAL FIREARMS CORP
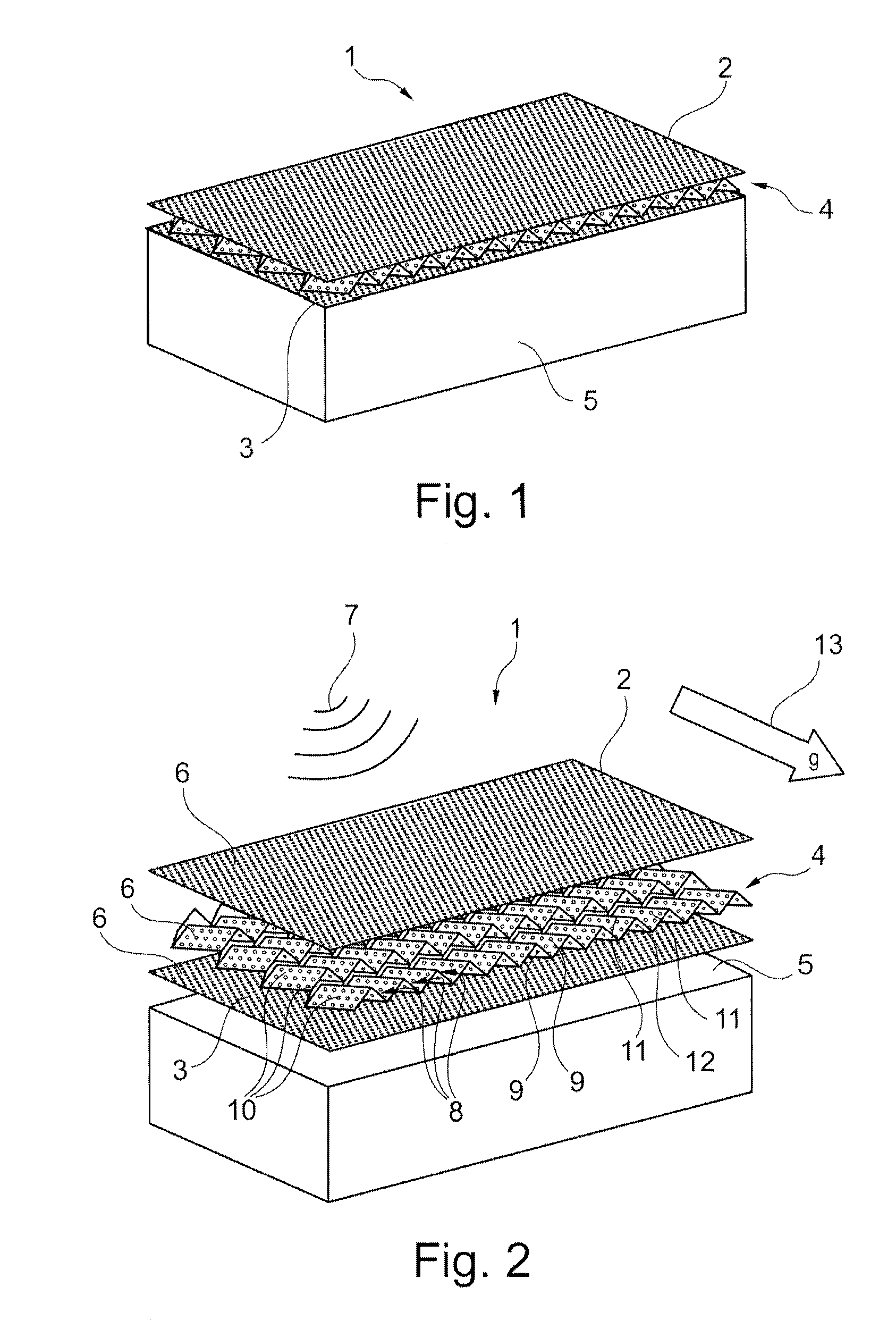
Sandwich element for the sound-absorbing inner cladding of means of transport, especially for the sound-absorbing inner cladding of aircraft
InactiveUS20110100747A1Slow down propagationReadily heatWallsFuselage insulationAcoustic absorptionAirplane
Owner:AIRBUS OPERATIONS GMBH
Enhanced performance mode converter
ActiveUS7242821B2Reduce accumulationPropagation delayCoupling light guidesOptical waveguide light guideSemiconductor materialsSchottky barrier
An optical mode converter comprising a slow wave electrode structure and including Schottky barriers for preventing an accumulation of free carriers in the optical waveguide region of the converter. The Schottky barriers are also used for suppressing higher order modes in the waveguide. Low refractive index insulators are used to allow efficient driving of the device without hindering the impedance or the microwave index of the optical mode converter. Two-photon absorption processes are eliminated through the use of a waveguide semiconductor material having a bandgap of at least twice the photon energy of the light beam propagating through the optical mode converter.
Owner:OPTELIAN ACCESS NETWORKS
Secondary Battery
ActiveUS20110212350A1Propagation delayFinal product manufactureCell lids/coversInternal pressureEngineering
A secondary battery includes a gas release valve located at a battery container housing a power generating element, wherein: the gas release valve includes a valve disk caused to expand outward by internal pressure in the battery container; wherein a plurality of grooves are formed at the valve disk in order that a plurality of valve element pieces become fractured along the grooves when the valve disk expands due to the internal pressure; and a scatter-deterring portion is formed at the valve disk in order to prevent the fractured valve element pieces along the grooves from scattering away from the valve disk.
Owner:HITACHI VEHICLE ENERGY
Monolithic firearm suppressor
A monolithic suppressor for suppressing sounds generated by the discharge of a firearm, wherein the discharge generates propellant gases. The monolithic suppressor includes a bore having a first end and a second end, the first end having an inlet aperture and the second end having an outlet aperture. In addition, a plurality of baffles are disposed within the bore, wherein the plurality of baffles further define a plurality of chambers. The chambers of the suppressor include at least an arcuate baffle and a slanted baffle. The plurality of chambers are configured to cause the propellant gases to spin in a plurality of vortices within one or more of the chambers thereby slowing the propagation of the gases within the suppressor.
Owner:TEMPLAR TACTICAL FIREARMS CORP
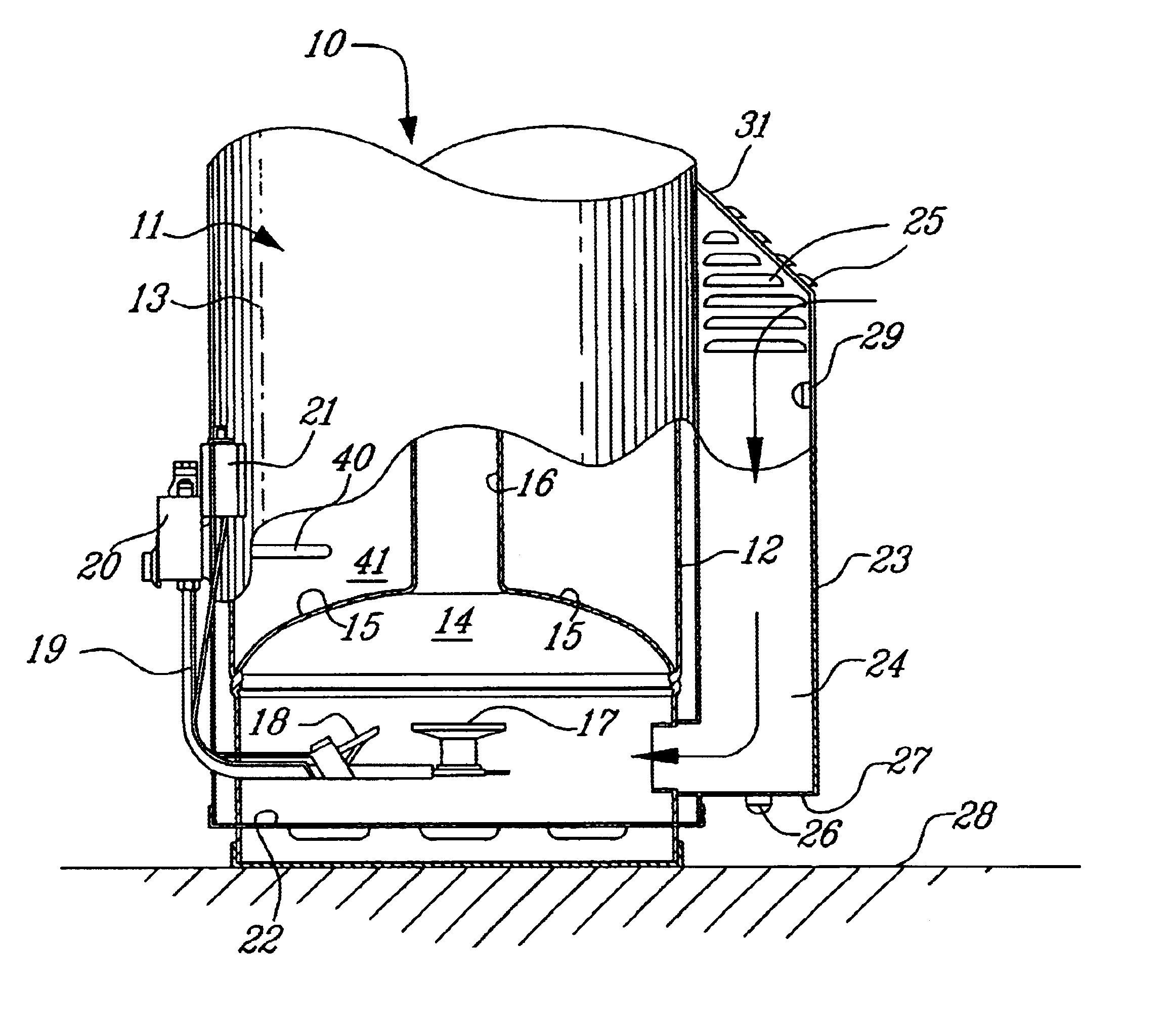
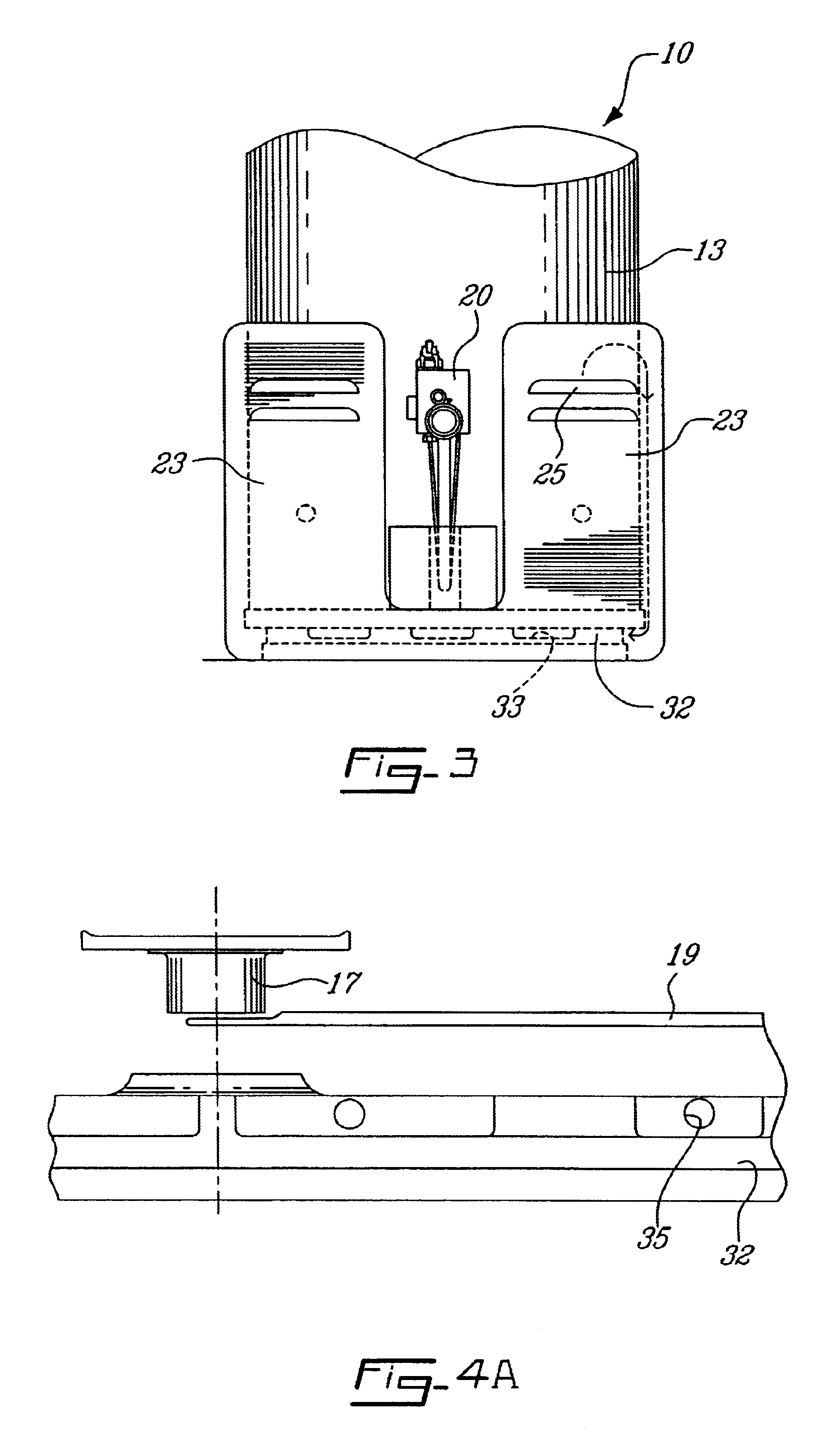
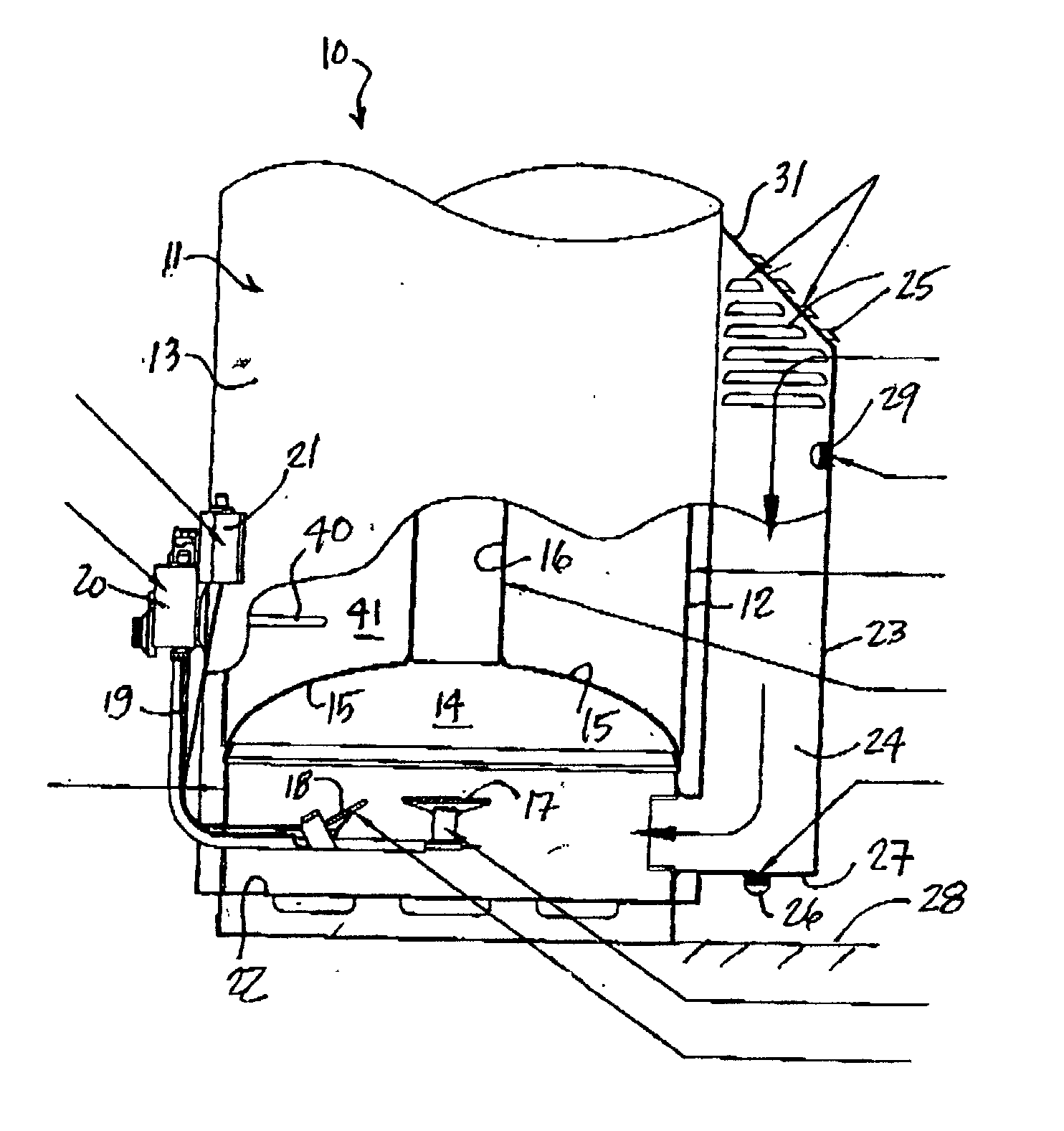
Explosion proof gas-fired water heater
InactiveUS6662757B2Enough timePropagation delayDrum steam boilersWater heatersCombustion chamberFresh air
An explosion proof gas-tired water heater is comprised of a housing having a water reservoir provided with a sealed combustion chamber thereunder. A flue pipe is disposed above the combustion chamber and extends through the reservoir. A gas burner and pilot are provided in the combustion chamber. At least one air supply channel is provided to supply fresh air to the combustion chamber. The air supply channel has an intake disposed a predetermined height above the floor to prevent combustible vapors from entering the combustion chamber. Vapor detectors and / or pressure sensors may be provided as added features to detect the presence of combustible vapors as well as the production of harmful carbon monoxide in the combustion chamber and to actuate the gas supply cut-off valve.
Owner:MICLAU S R I
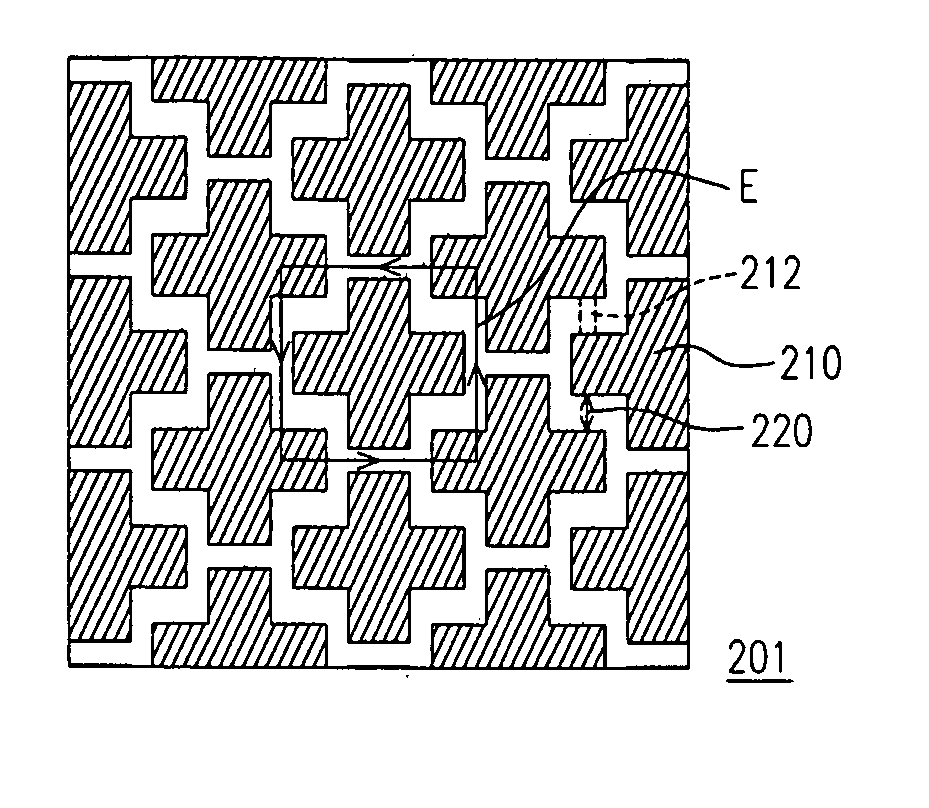
Ground shield structure
InactiveUS20050016746A1Decrease circuit layout areaReduce energy lossElectrically conductive connectionsPrinted circuit detailsGround planeCapacitance
A ground shield structure is suitable for use in a circuit structure. The ground shield structure has a plurality of ground cells that are arranged on a ground plane periodically, compactly and complementarily. The slots between the ground cells are used to reduce the eddy current generated on the ground shield structure. The ground shield structure increases the slow-wave factor to slow the waves so that the area of the circuit layout can be decreased. Besides, the ground shield structure can reduce the energy loss of the inner circuit of the circuit structure and can increase the quantities of inductance and capacitance in per unit area thereon.
Owner:VIA TECH INC
Enhanced copper posts for wafer level chip scale packaging
ActiveUS7820543B2Increased shear strengthIncrease surface areaSemiconductor/solid-state device detailsSolid-state devicesSolder ballElectrical connection
An enhanced wafer level chip scale packaging (WLCSP) copper electrode post is described having one or more pins that protrude from the top of the electrode post. When the solder ball is soldered onto the post, the pins are encapsulated within the solder material. The pins not only add shear strength to the soldered joint between the solder ball and the electrode post but also create a more reliable electrical connection due to the increased surface area between the electrode post / pin combination and the solder ball. Moreover, creating an irregularly shaped solder joint retards the propagation of cracks that may form in the intermetal compounds (IMC) layer formed at the solder joint.
Owner:ADVANCED MFG INNOVATIONS INC
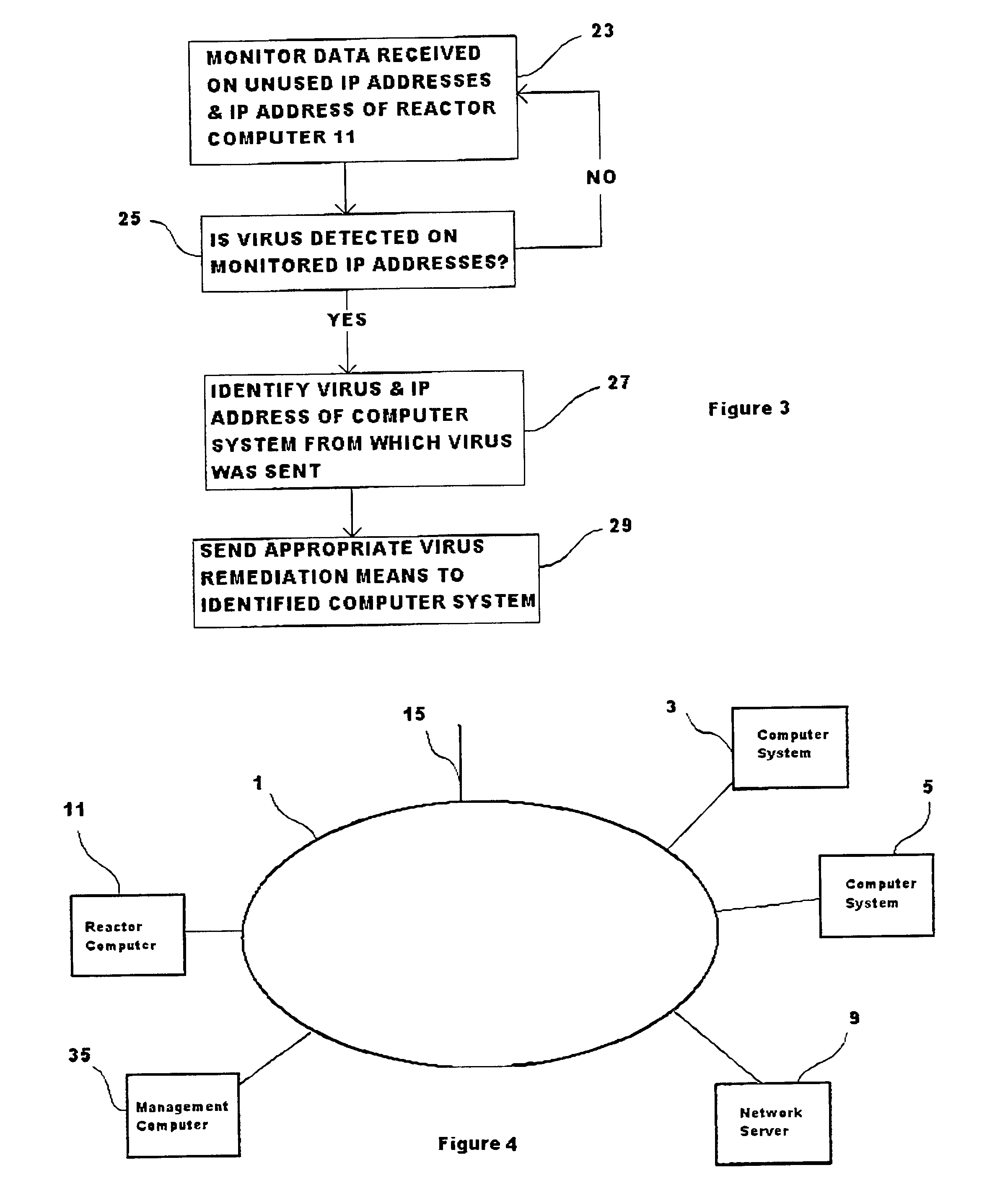
Method of hindering the propagation of a computer virus
ActiveUS7278019B2Hinders its propagationReduce stepsMemory loss protectionUser identity/authority verificationComputerized systemVirus
A method of hindering the propagation of a computer virus on a computer network is disclosed. The computer network comprises a plurality of addressable connections capable of receiving data from at least one computer system, and a detection computer arranged to detect the presence of a computer virus. The method comprises: operating the detection computer to monitor the plurality of addressable connections thereby to detect the presence of a computer virus on at least one of the addressable connections; in the event that a computer virus is detected, identifying the at least one computer system that sent the computer virus to the at least one addressable connection; and sending virus remediating means to the at least one identified computer system, the virus remediating means being arranged at least to hinder the operation of the computer virus. A computer program and computer system for hindering the propagation of a computer virus is also disclosed.
Owner:HEWLETT PACKARD DEV CO LP
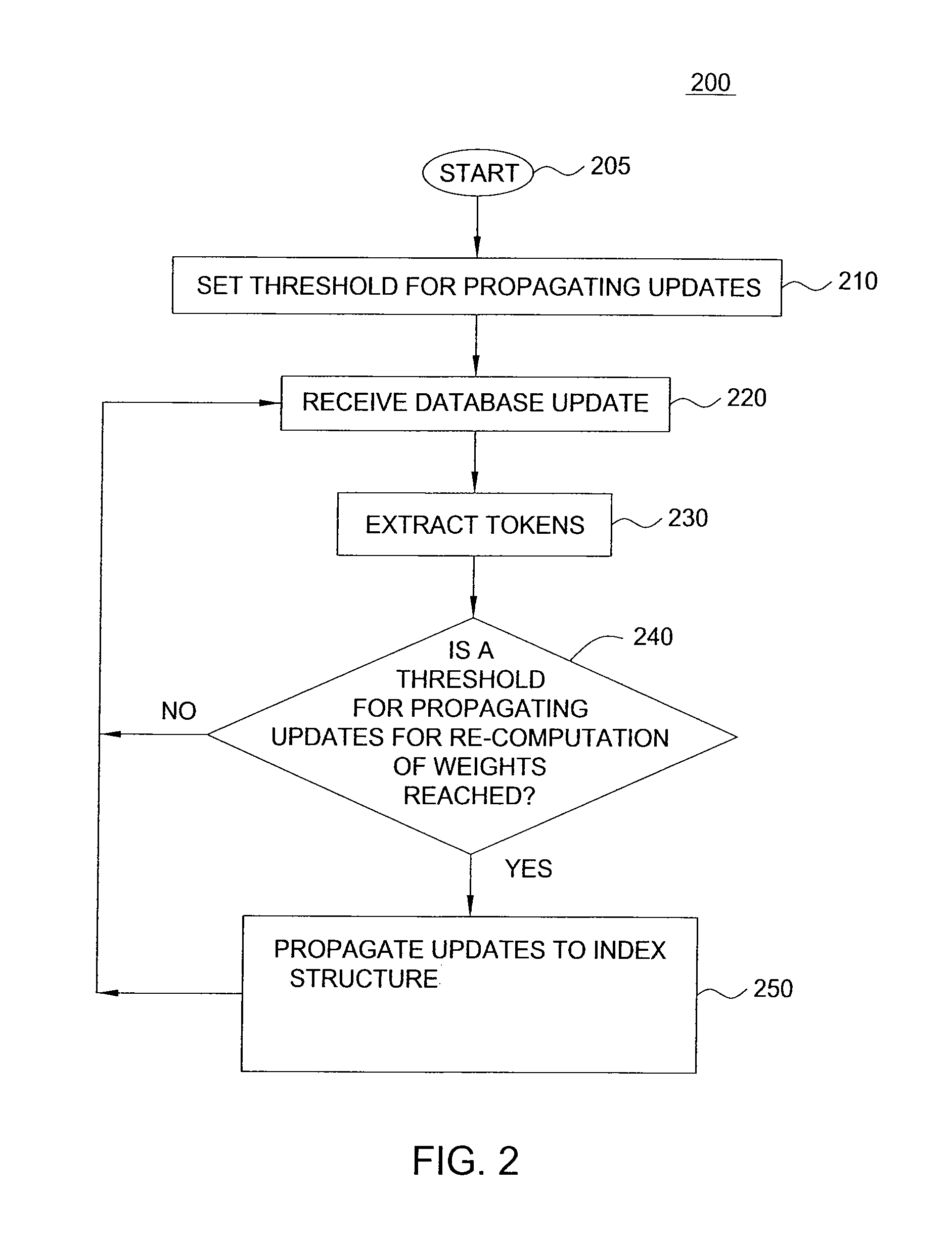
Method and apparatus for propagating updates in databases
InactiveUS8645397B1Propagation delayLimit propagationDigital data information retrievalDigital data processing detailsPhases of clinical researchData mining
A method and apparatus for propagating updates in databases are disclosed. For example, the present method uses “blocking” and / or “thresholding” to delay update propagation and / or to limit the propagation of updates to an optimal stage. For example, the present method receives at least one database update and extracts at least one token from the at least one database update. The method then determines whether a threshold for propagating the at least one database update for the at least one token is reached. The method then propagates the at least one database update for updating an index structure of a database pertaining to the at least one token whose threshold has been reached.
Owner:AMERICAN TELEPHONE & TELEGRAPH CO
Ground shield structure
InactiveUS20060254814A1Reduce needPropagation delayPrinted circuit detailsMagnetic/electric field screeningEngineering
The invention is directed to an electric device featuring a ground shield structure. The electric device at lease comprises a plurality of first ground cells and a plurality of second ground cells. The first ground cells are distributed on a ground surface, wherein the first ground cell has at least one first outward section and at least one first inward section. The second ground cells are distributed on the ground surface, wherein the second ground cell has at least one second outward section and one second outward section of one second ground cell is compactly and complementarily embraced by one first inward section of one adjacent first ground cell.
Owner:SZE BOURYI +3
Explosion proof gas-fired water heater
InactiveUS20030150404A1Enough timePropagation delayWater heatersAir/fuel supply for combustionCombustion chamberFresh air
An explosion proof gas-tired water heater is comprised of a housing having a water reservoir provided with a sealed combustion chamber thereunder. A flue pipe is disposed above the combustion chamber and extends through the reservoir. A gas burner and pilot are provided in the combustion chamber. At least one air supply channel is provided to supply fresh air to the combustion chamber. The air supply channel has an intake disposed a predetermined height above the floor to prevent combustible vapors from entering the combustion chamber. Vapor detectors and / or pressure sensors may be provided as added features to detect the presence of combustible vapors as well as the production of harmful carbon monoxide in the combustion chamber and to actuate the gas supply cut-off valve.
Owner:MICLAU S R I
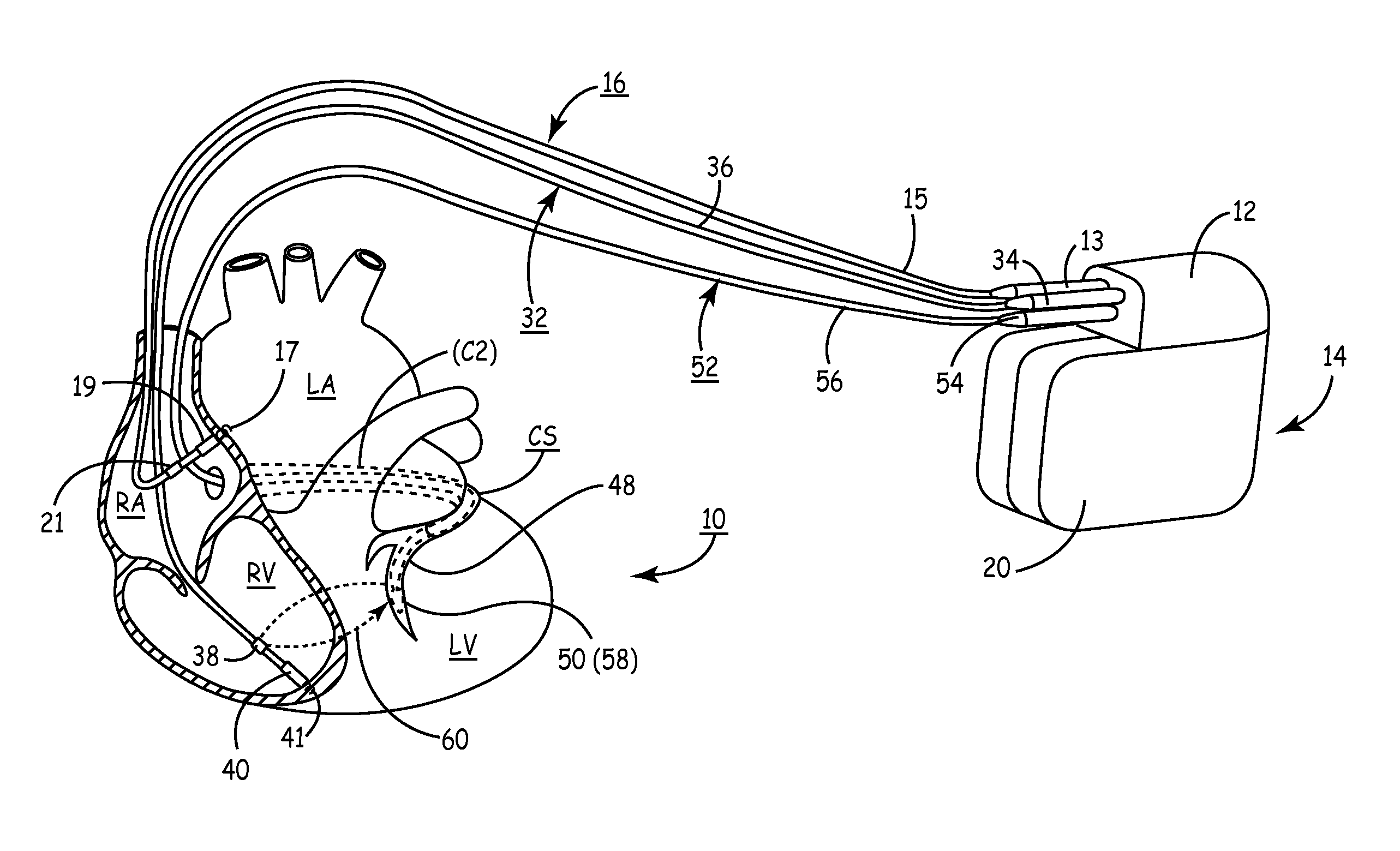
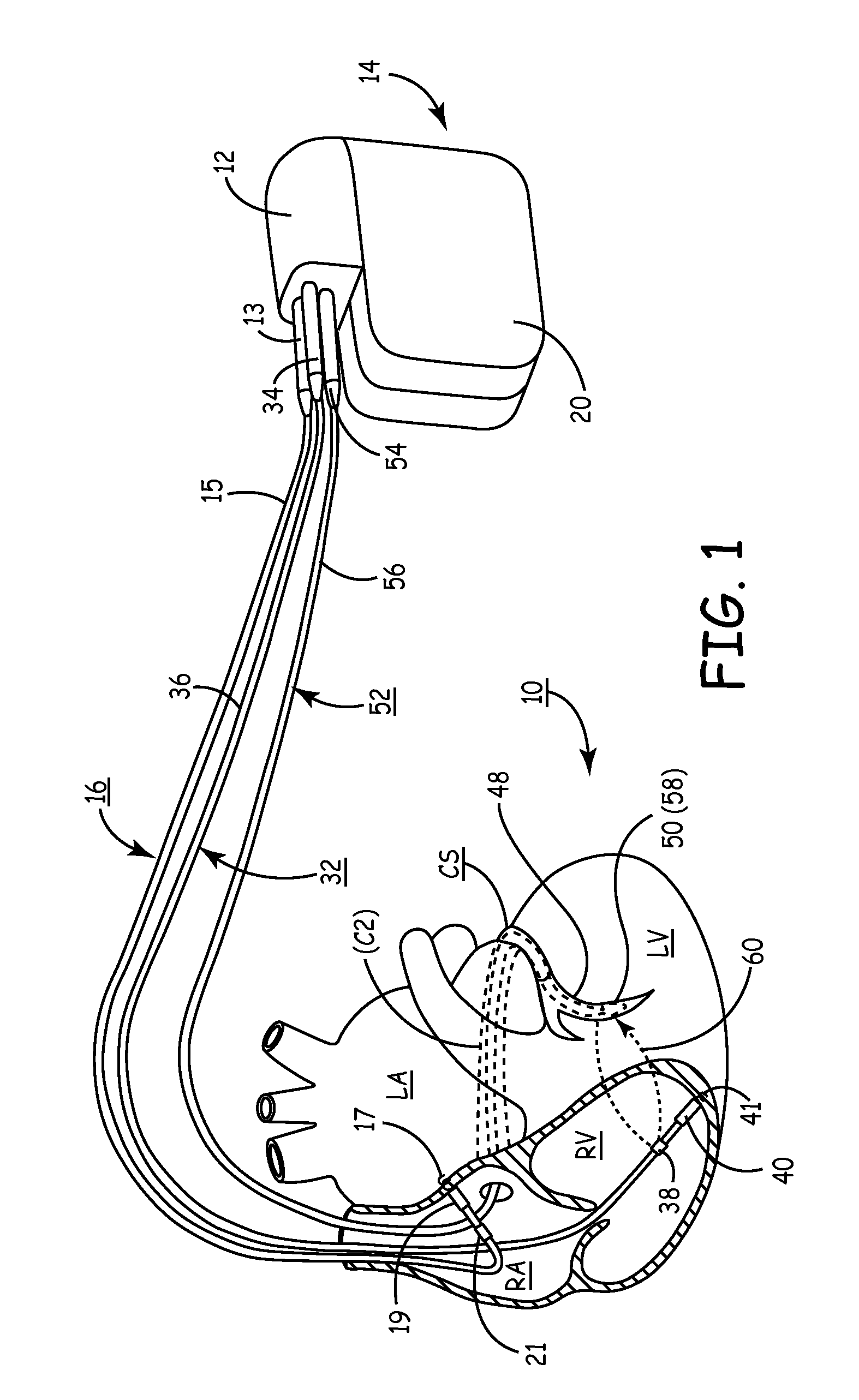
Implantable medical device for cardiac electrical stimulation
InactiveUS20100298901A1Reduce rateReduce pressureElectrocardiographyCatheterNODALVentricular depolarization
A method and apparatus for reducing a patient's heart rate or blood pressure. The apparatus provides stimulation to the patient's atrial and / or nodal tissue within the associated refractory period of the ventricle but outside of an associated refractory period of the stimulated atrial an / or nodal tissue, responsive to detecting an occurrence of a ventricular depolarization following a preceding atrial depolarization.The apparatus may define a time window following the ventricular depolarization, following the atrial depolarization or determined based upon the timing of both the atrial and ventricular depolarizations. The stimulus may be delivered during or on expiration of the defined time window. The duration of the time window may be pre-set or determined based upon measurements of the patient's refractory periods.
Owner:MEDTRONIC INC
Method for calculating a local extremum, preferably a local minimum, of a multidimensional function E(x1, x2, ..., xn)
InactiveUS20070239809A1Fast conductionFast and accurate methodDigital data processing detailsDigital computer detailsVelocity vectorComputer science
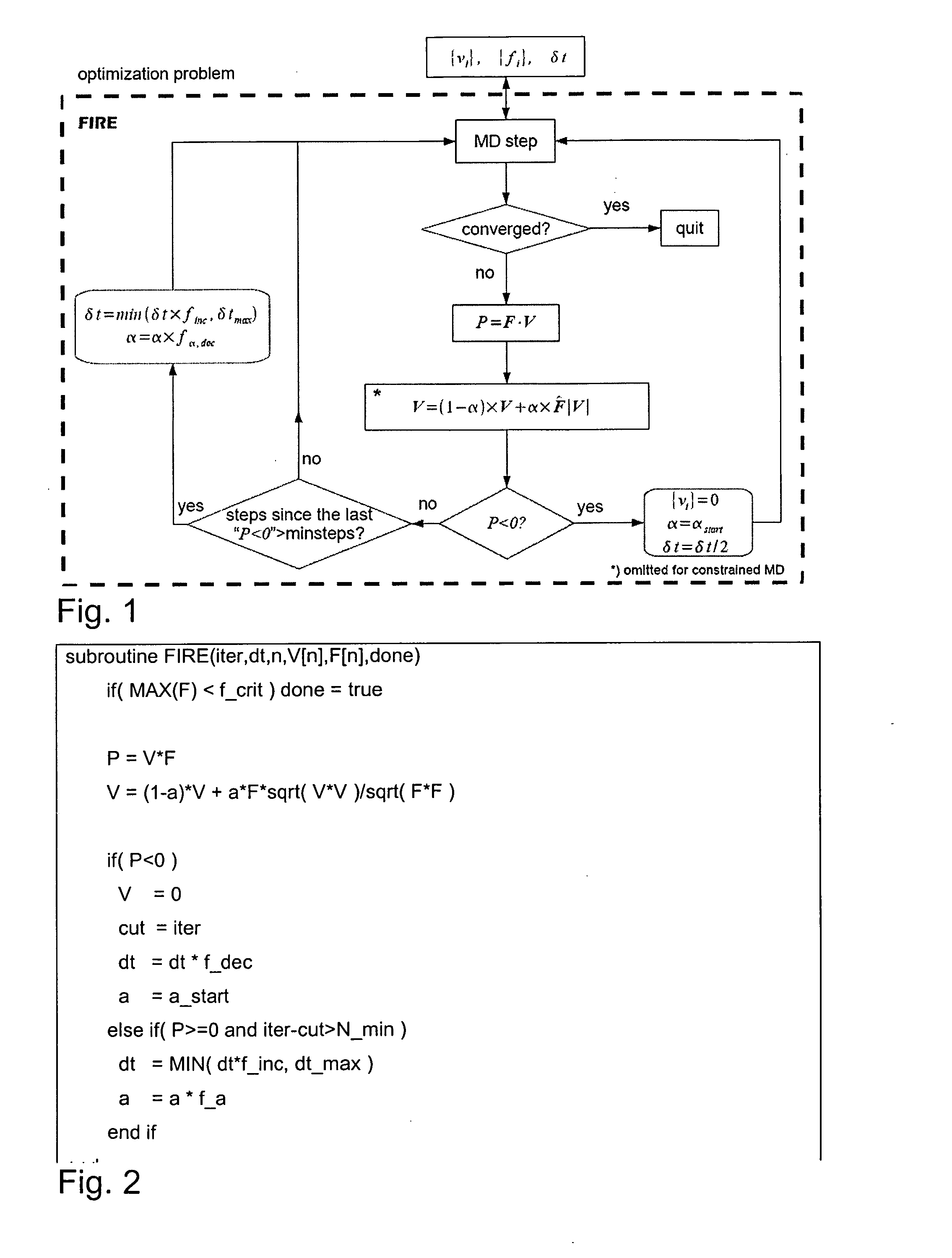
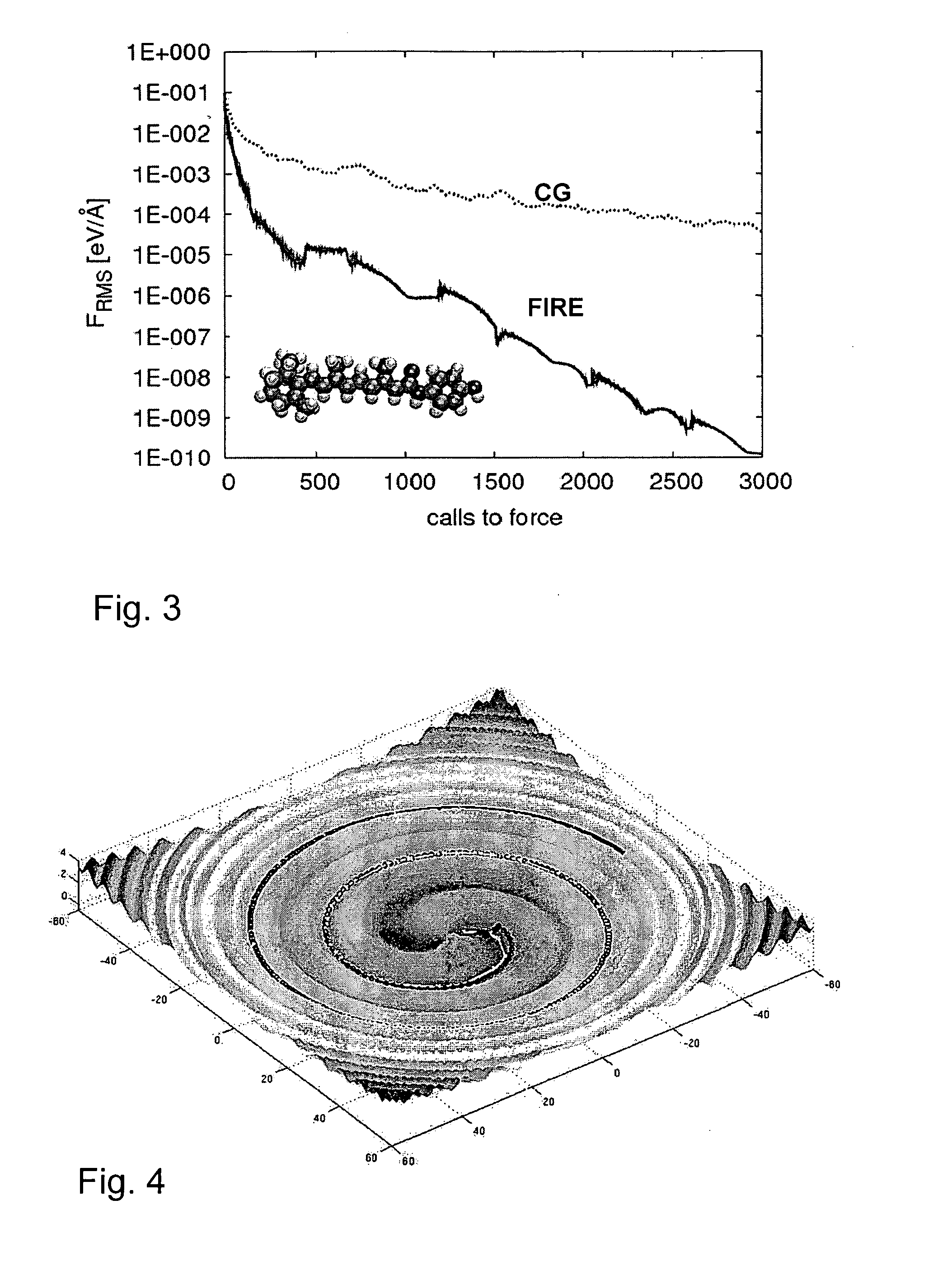
The invention relates to a Method for calculating a local extremum, preferably a local minimum, of a multidimensional function E(x1, x2, . . . , xn) which is interpretable as a function of potential energy with spatial coordinates (x1, x2, . . . , xn), using an iteration process based on a molecular dynamics based quenching method comprising the following steps: a) Calculating a trajectory X(ti) at discrete times ti=Σiδti starting from an assigned initial coordinate X(0) on basis of a gradient fk=δE / δxk with k=1, . . . ,n and a time derivatives of the coordinates vk=dxk / dt using fxk=mxk dvxk / dt in which mxk represent masses at the spatial coordinates and vxk=dxk / dt represents velocity b) Performing a molecular dynamics based quenching method for analysing said function E(x1, x2, . . . , xn) of existence of a local extremum, in case of reaching a local extremum abort processing and / or select a new initial coordinate and proceed further from step a) c) Calculating at each iteration time step δti F=(fxk) and (k=1, . . . ,n) representing a global force vector field acting in the spatial coordinates, V=(vxk) representing a velocity vector field, P=F·V representing power Setting V=(1−α)×V+α×(F / |F|)·|V|α is a dimensionless variable and amounts a given initial value αstart at first iteration time step In case of P<0: V is set to zero, α becomes αstart, δti will be reduced and return to step b) In case of P≧0: Analysing whether the number of conducted iteration steps since the last detected case of P<0 exceeds a given minimum number Nmin, in case of “no” returning to step b) and in case of “yes” increasing δti, decreasing α and return to step b).
Owner:FRAUNHOFER GESELLSCHAFT ZUR FOERDERUNG DER ANGEWANDTEN FORSCHUNG EV
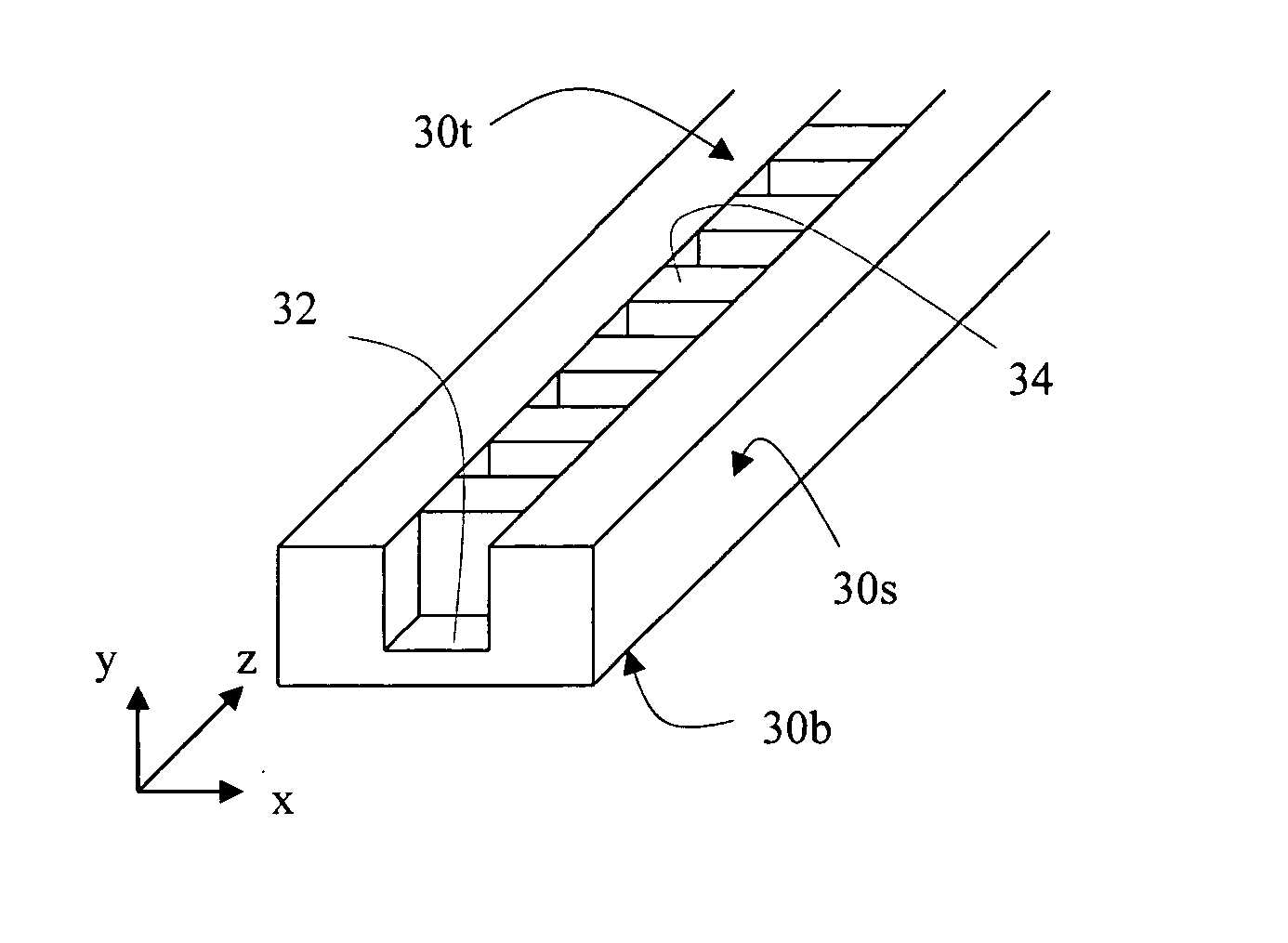
Slow-wave structure for ridge waveguide
Owner:NORTHROP GRUMMAN SYST CORP
Optical fibre network
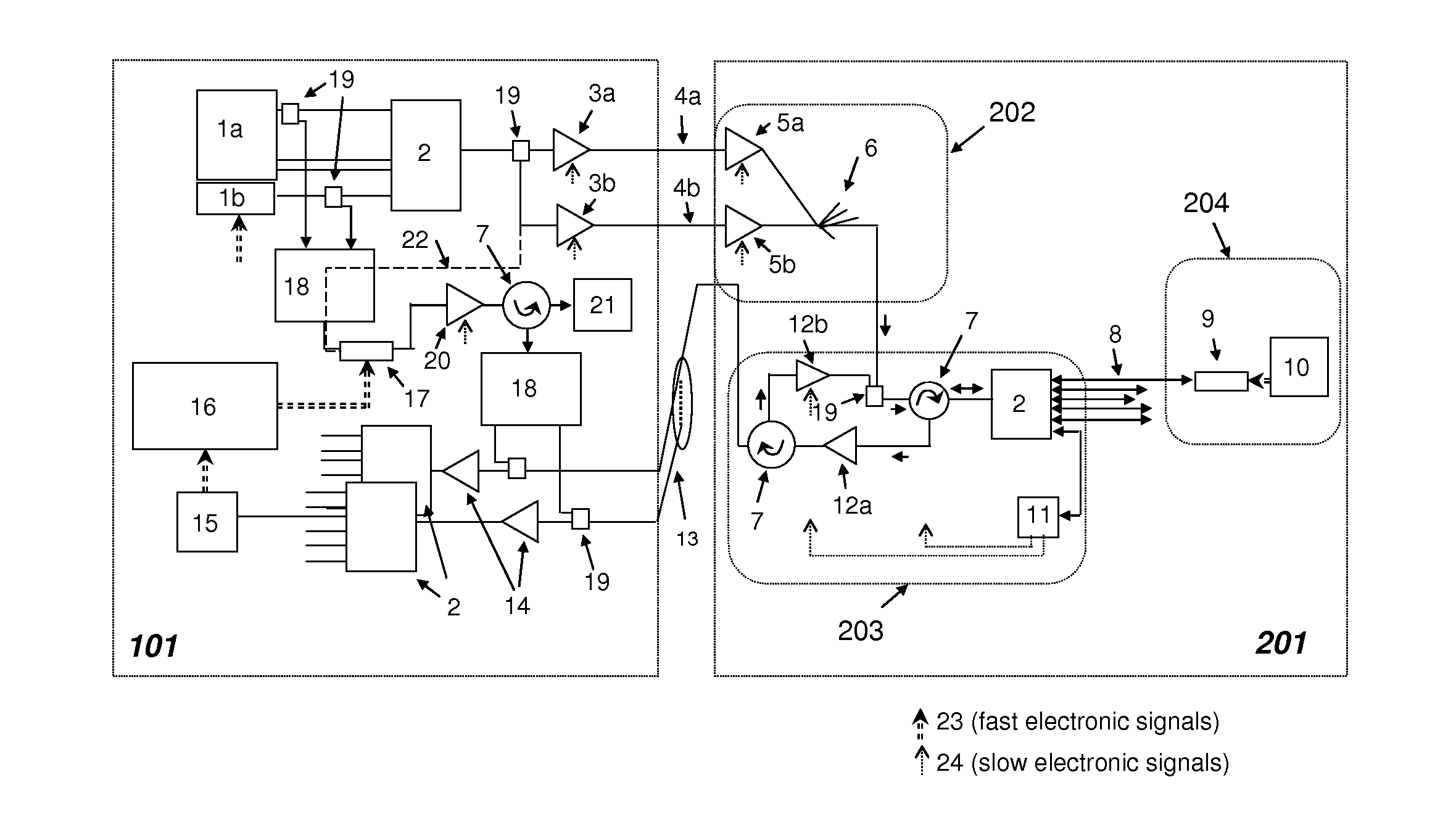
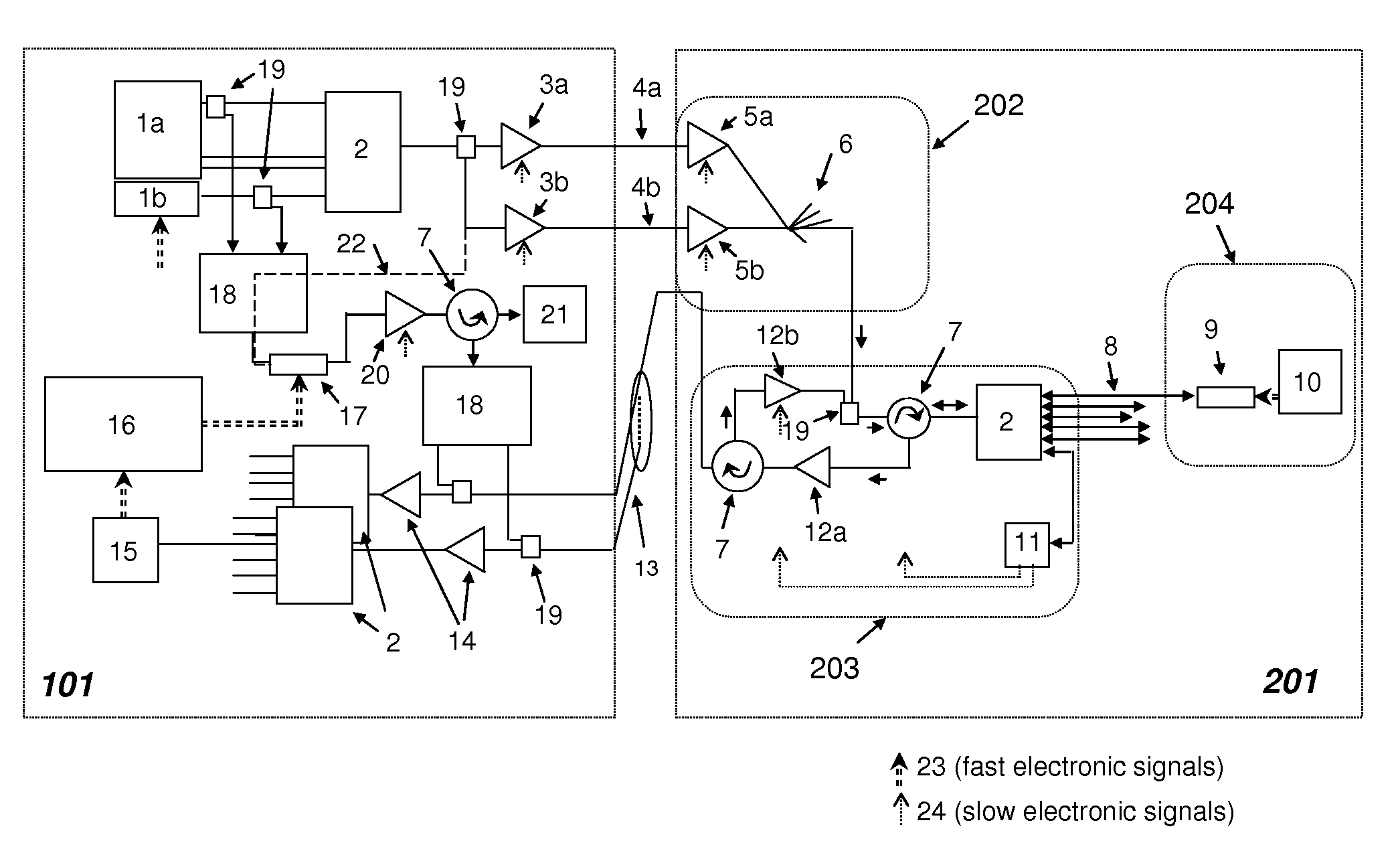
ActiveUS20100266285A1Reduce maximum bit-ratePropagation delayTime-division optical multiplex systemsWavelength-division multiplex systemsMultiplexingMultiplexer
An optical fibre network comprises a laser source (1a) configured to generate laser light of a plurality of wavelengths. A first optical fibre (4a), transmits multi-wavelength light from the laser source to a location remote from the laser source. A wavelength division multiplexer (2) at the remote location (203) is connected to a plurality of second optical fibres (8). A plurality of optical modulators (9) are each connected optically to the wavelength division multiplexer (2) via a respective second optical fibre (8). The wavelength division multiplexer (2) is arranged to de-multiplex the multi-wavelength light received from the first optical fibre (4a) into a plurality of wavelengths and to supply a respective wavelength to each of the second optical fibres (8). The optical modulators (9) are reflective optical modulators each arranged to modulate light received from the associated second optical fibre (8) with a data signal and to reflect the modulated light back along the second optical fibre (8). The wavelength division multiplexer (2) is arranged to multiplex the modulated light from all of the second optical fibres (8) into a wavelength division multiplexed optical signal for onward transmission along a third optical fibre (13).
Owner:HUAWEI TECH CO LTD
Sorting device and method
InactiveUS7866484B2Reduce transmissionPropagation delayGas current separationSortingVertical edgeEngineering
The invention relates to a sorting device and method for sorting granulated mass containing varied materials, such as granulated mass containing varied materials, such as granulated electronic scrap. According to the invention, the sorting device comprises a planar, elongated trough conveyor (1) having at least a first elongated and vertical edge (2, 3, 4); a feeding device (5) for feeding the mass into the first end (6) of the trough conveyor; a vibrator (9) provided with a motor (7) and an eccentric (8), whose rotation axis (10) is disposed in a plane deviating from the plane defined by the trough conveyor so that the mass proceeds obliquely forwards in the trough conveyor towards the first edge and second end (11); a first suction device (12) for removing the lightest surface portion of the mass near the edge, a guide (13) which is oblique with respect to the edge for bringing apart the mass flow from the edge; as well as a mechanical separator member (14) for dividing the mass flow into two parts.
Owner:RANTASALMEN SCEL
Managing access to a network
ActiveUS7647634B2Propagation delayMemory loss protectionUnauthorized memory use protectionDistributed computing
Owner:MICROSOFT TECH LICENSING LLC
Enhanced performance mode converter
ActiveUS20060067634A1Reduce disadvantagesReduce accumulationCoupling light guidesOptical waveguide light guideSemiconductor materialsSchottky barrier
An optical mode converter comprising a slow wave electrode structure and including Schottky barriers for preventing an accumulation of free carriers in the optical waveguide region of the converter. The Schottky barriers are also used for suppressing higher order modes in the waveguide. Low refractive index insulators are used to allow efficient driving of the device without hindering the impedance or the microwave index of the optical mode converter. Two-photon absorption processes are eliminated through the use of a waveguide semiconductor material having a bandgap of at least twice the photon energy of the light beam propagating through the optical mode converter.
Owner:OPTELIAN ACCESS NETWORKS
Optical fibre network
ActiveUS8606106B2Propagation delayImprove accuracyTime-division optical multiplex systemsWavelength-division multiplex systemsMultiplexingMultiplexer
An optical fiber network comprises a laser source (1a) configured to generate laser light of a plurality of wavelengths. A first optical fiber (4a), transmits multi-wavelength light from the laser source to a location remote from the laser source. A wavelength division multiplexer (2) at the remote location (203) is connected to a plurality of second optical fibers (8). A plurality of optical modulators (9) are each connected optically to the wavelength division multiplexer (2) via a respective second optical fiber (8). The wavelength division multiplexer (2) is arranged to de-multiplex the multi-wavelength light received from the first optical fiber (4a) into a plurality of wavelengths and to supply a respective wavelength to each of the second optical fibers (8). The optical modulators (9) are reflective optical modulators each arranged to modulate light received from the associated second optical fiber (8) with a data signal and to reflect the modulated light back along the second optical fiber (8). The wavelength division multiplexer (2) is arranged to multiplex the modulated light from all of the second optical fibers (8) into a wavelength division multiplexed optical signal for onward transmission along a third optical fiber (13).
Owner:HUAWEI TECH CO LTD
Cooling of a gas turbine component designed as a rotor disk or turbine blade
InactiveUS8956116B2Extended service lifeReduce stress concentrationPropellersEngine manufactureStress concentrationTurbine blade
A gas turbine component for example a turbine blade or a rotor disk is provided. In order to extend the service life of the corresponding component by reducing the thermally or mechanically induced stress concentration in the direct surroundings of a duct opening onto a surface, at least one groove-like recess is provided near the effective zone of the opening.
Owner:SIEMENS AG
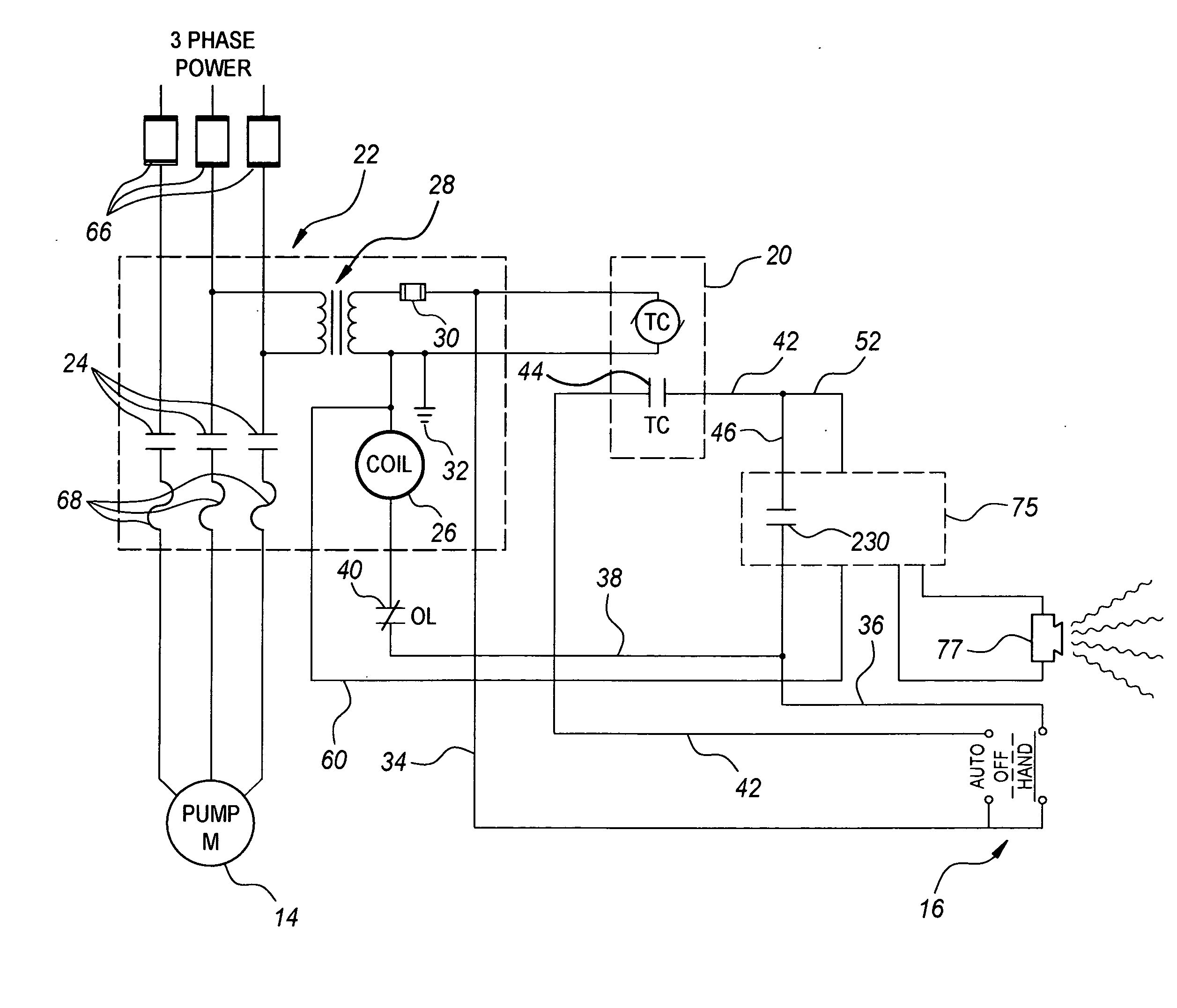
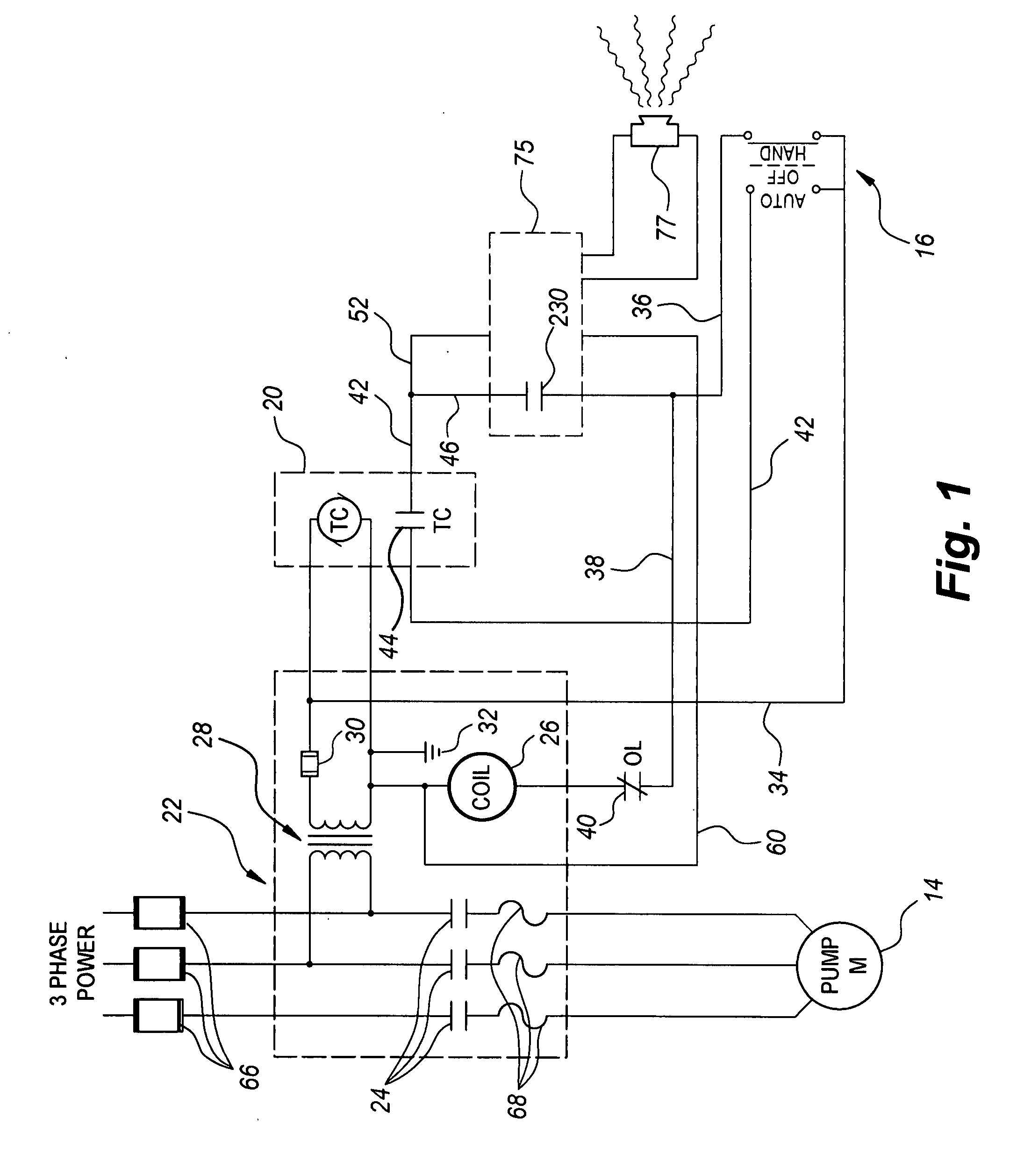
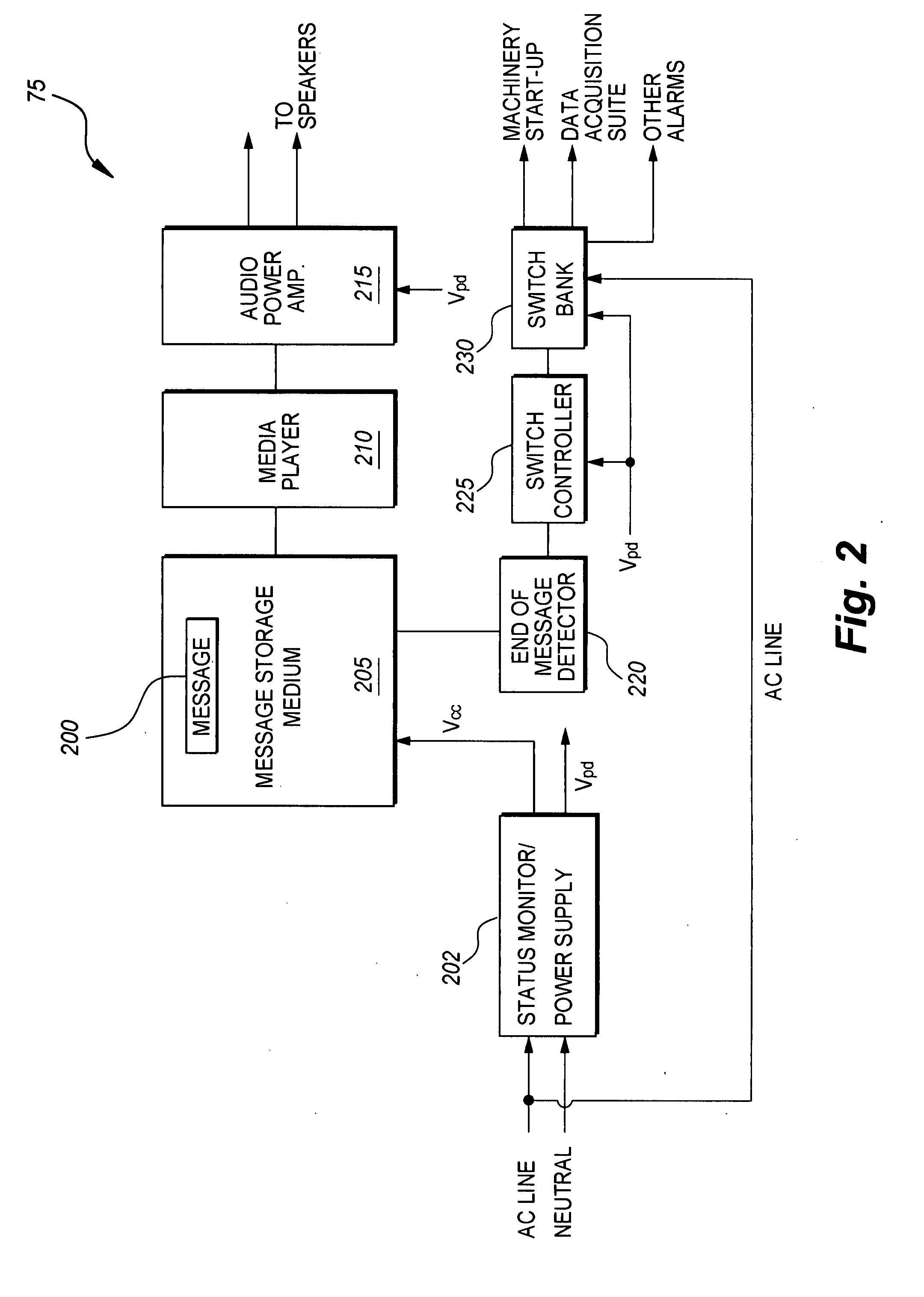
Delayed start-up verbal warning unit
InactiveUS20080048840A1Avoid injuryPropagation delaySignalling system detailsElectric/electromagnetic audible signallingSCADAOil well
The delayed start-up verbal warning unit includes an audible alarm that comprises a verbal warning and instructions. The unit is connected to a control circuit for machinery, e.g., an oil well pumping unit. The control circuit includes a means of generating a start-up signal for the machinery. Where the machinery is an oil well pumping unit, the unit operates to issue a verbal warning and instructions related to imminent start-up of the pumping unit. Playback of the verbal warning delays propagation of the start-up signal to the pump, thereby providing people in the area the opportunity to avoid injury by evacuating the area. Additionally, start-up signal status may be sent by the unit to a Supervisory Control And Data Acquisition (SCADA) system for further processing and analysis.
Owner:PROTECH SAFETY SYST
Managing access to a network
ActiveUS20070016679A1Propagation delayMemory loss protectionUnauthorized memory use protectionDistributed computingHost machine
Owner:MICROSOFT TECH LICENSING LLC
Slow-wave structure for ridge waveguide
A ridge waveguide filter having a slow-wave structure. The ridge waveguide has an elongate hollow tube formed of a conductive sidewall. At least a first part of the conductive sidewall periodically is recessed along an elongate direction of the hollow tube, such that a plurality of ridges is formed to project in the hollow tube. The sidewall is fabricated from metallic materials. The hollow tube includes a rectangular hollow tube or a circular hollow tube, for example. The ridges are equally spaced from and parallel with each other. Each of the ridges has a bottom surface parallel with a second part of the conductive sidewall. The second part of the conductive sidewall is opposite to the first part of the conductive sidewall.
Owner:NORTHROP GRUMMAN SYST CORP
Cooling of a Gas Turbine Component Designed as a Rotor Disk or Turbine Blade
InactiveUS20120207615A1Extended service lifeReduce stress concentrationEngine manufactureEngine fuctionsStress concentrationTurbine blade
A gas turbine component for example a turbine blade or a rotor disk is provided. In order to extend the service life of the corresponding component by reducing the thermally or mechanically induced stress concentration in the direct surroundings of a duct opening onto a surface, at least one groove-like recess is provided near the effective zone of the opening.
Owner:SIEMENS AG
Sorting Device and Method
InactiveUS20080128337A1Reduce transmissionPropagation delaySievingGas current separationEngineeringElectronic scrap
The invention relates to a sorting device and method for sorting granulated mass containing varied materials, such as granulated mass containing varied materials, such as granulated electronic scrap. According to the invention, the sorting device comprises a planar, elongated trough conveyor (1) having at least a first elongated and vertical edge (2, 3, 4); a feeding device (5) for feeding the mass into the first end (6) of the trough conveyor, a vibrator (9) provided with a motor (7) and an eccentric (8), whose rotation axis (10) is disposed in a plane deviating from the plane defined by the trough conveyor so that the mass proceeds obliquely forwards in the trough conveyor towards the first edge and second end (11); a first suction device (12) for removing the lightest surface portion of the mass near the edge, a guide (13) which is oblique with respect to the edge for bringing apart the mass flow from the edge; as well as a mechanical separator member (14) for dividing the mass flow into two parts.
Owner:RANTASALMEN SCEL
System and method for efficient implementation of prime field arithmetic in arm processors
ActiveUS20190158284A1Communication securityPropagation delayPublic key for secure communicationCryptographic attack countermeasuresComputer hardwareComputer science
The present invention provides a method for performing Elliptic Curve Cryptography (ECC) on data, the ECC implemented on multiple arithmetic layers. By performing multi-precision multiplication by implementing product-scanning to process columns of intermediary results in order to obtain a multiplication result by computing unsigned multiplication of data, accumulating a result of the multiplication and preserving a generated carry flag such that propagation of the carry flag is delayed, the present invention improves performance.
Owner:LG ELECTRONICS INC +1
Method and arrangement for generating a jet of fluid, method and system for transforming the jet into a plasma, and uses of said system
InactiveUS9642233B2Propagation delayMedical devicesX-ray tube with very high currentJet flowSolenoid valve
Owner:CENT NAT DE LA RECHERCHE SCI +1
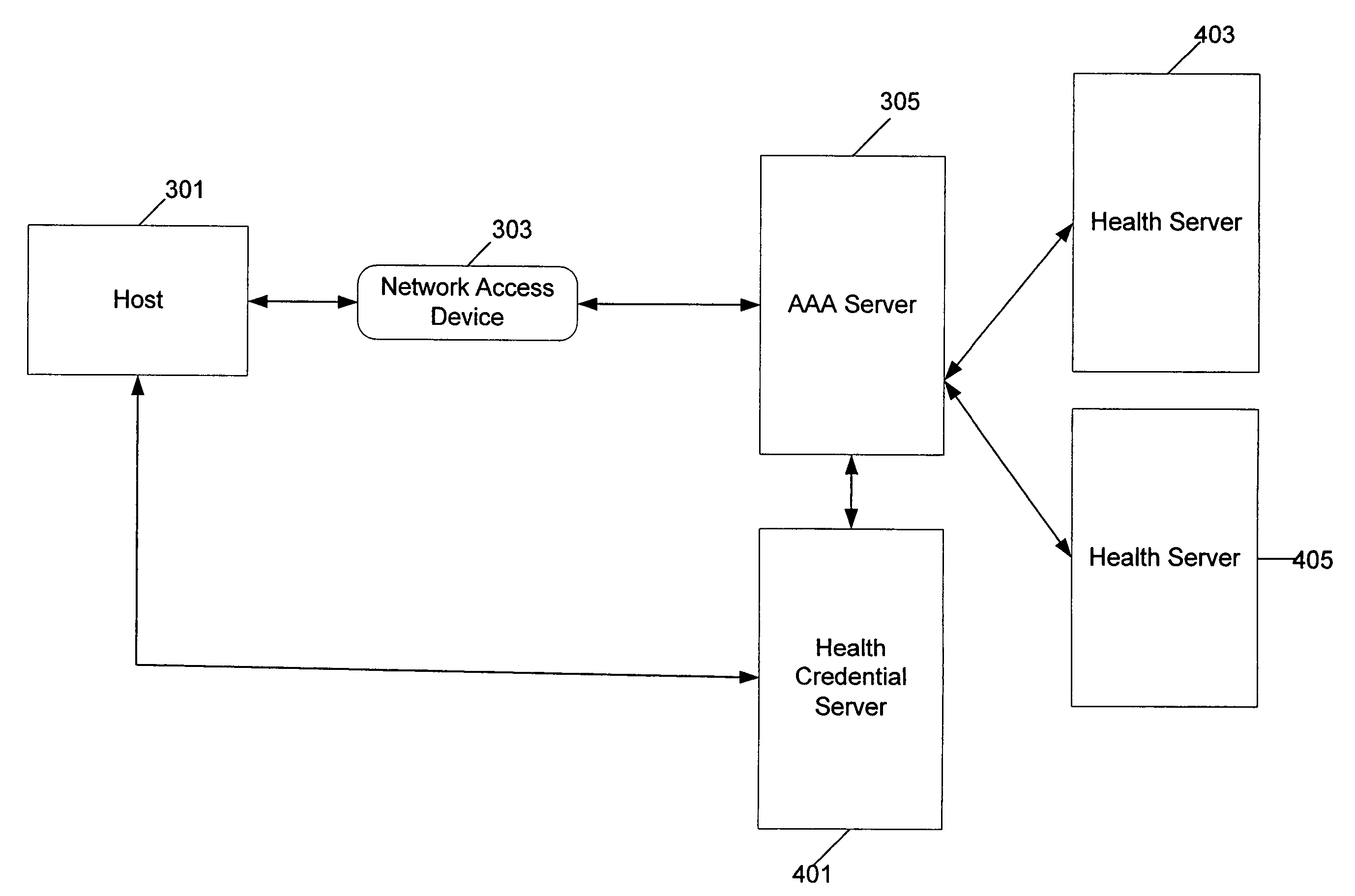
Method and apparatus for delaying propagation of patient healthcare data
InactiveUS20140297322A1Propagation delayGuaranteed accuracyData processing applicationsPatient personal data managementDelayed periodsPatient demographics
A method, apparatus and computer program product are therefore in order to provide delayed propagation of patient healthcare data. In this regard, methods, apparatuses, and computer program products may operate to control propagation of healthcare data for a delay period to ensure the accuracy of received medical data. This delay period may function to allow a record keeper to identify and correct any errors associated with the patient healthcare data. The delay period may be dynamic and configurable based on characteristics of the patient healthcare data. The delay period may be adjusted such that a threshold percentage of modifications are captured during the delay period. In some embodiments, the delay period may be associated with particular record characteristics, such as the record keeper that provided the record, a medical specialty associated with the record, patient demographic information, or the like.
Owner:MCKESSON FINANCIAL HLDG
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com