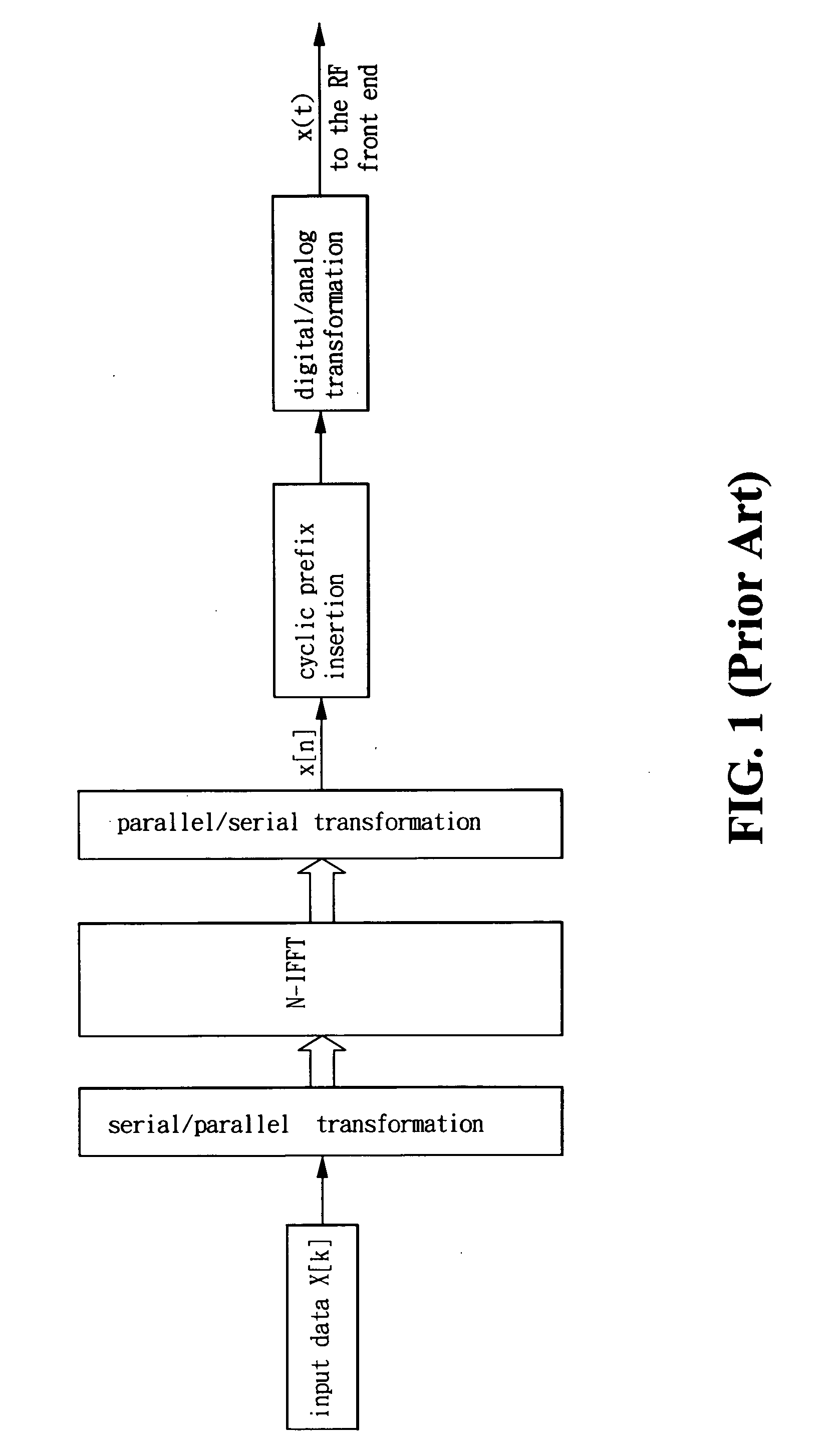
Patents
Literature
Hiro is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
5008 results about "Fast Fourier transform" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
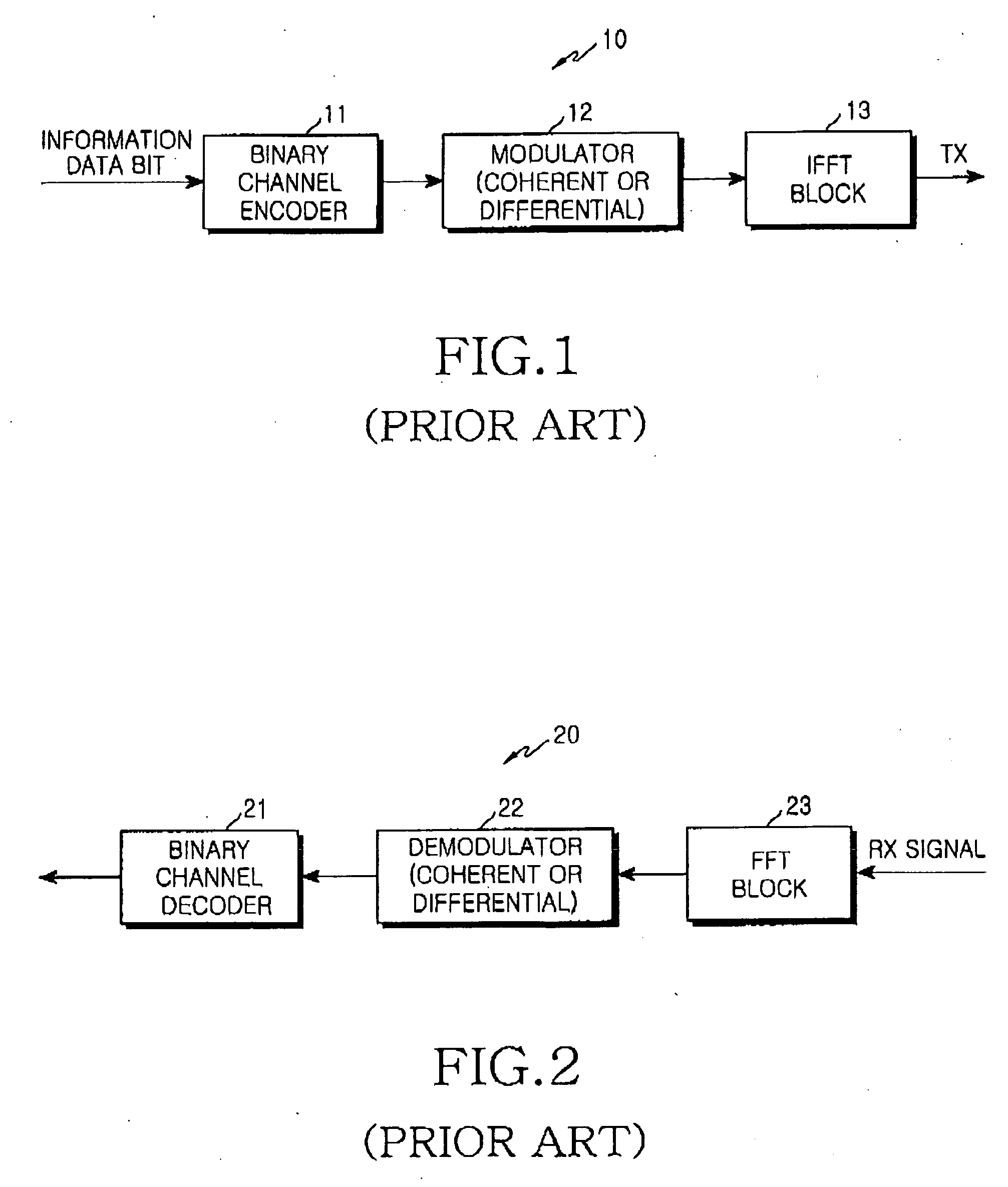
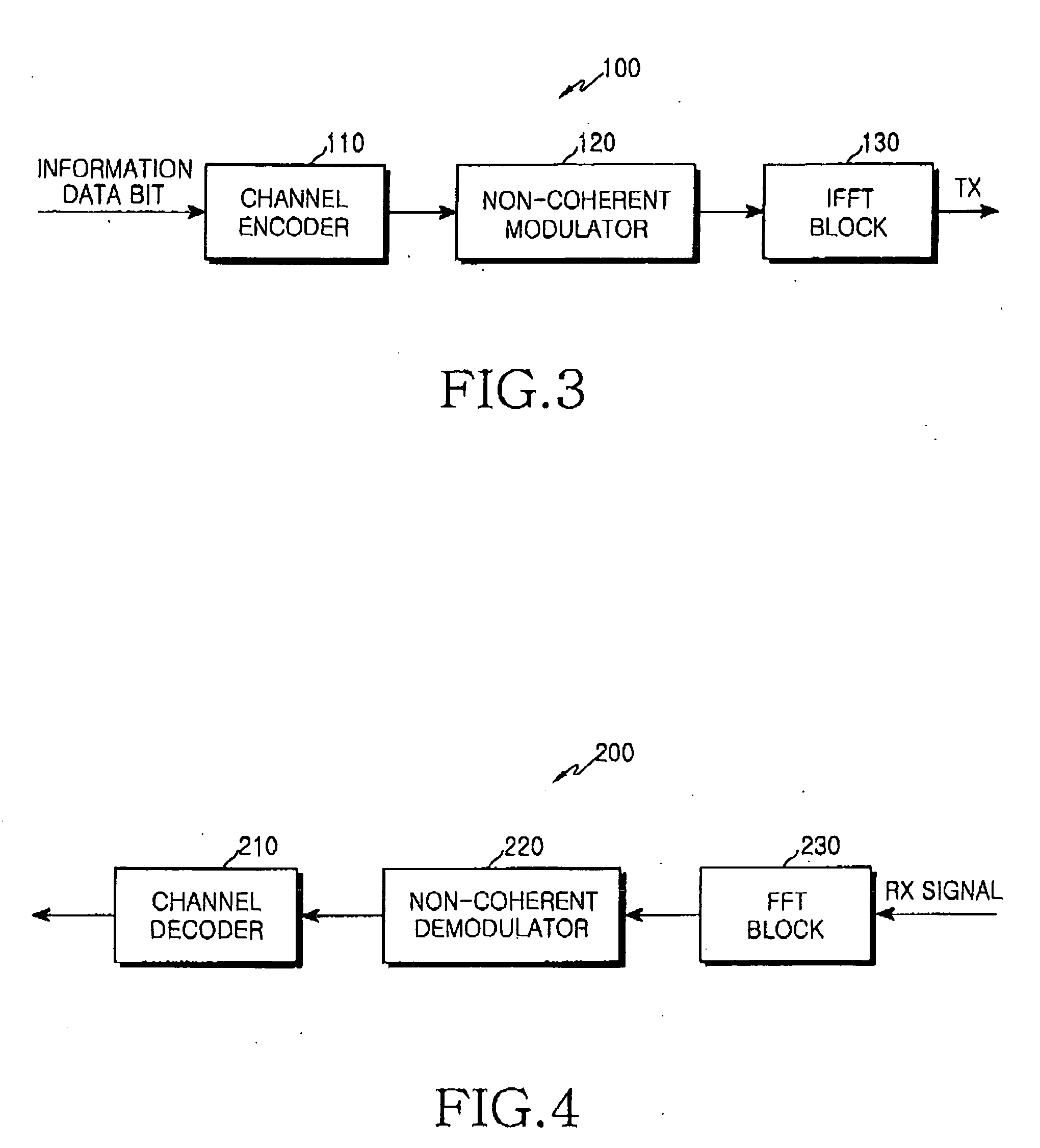
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical.
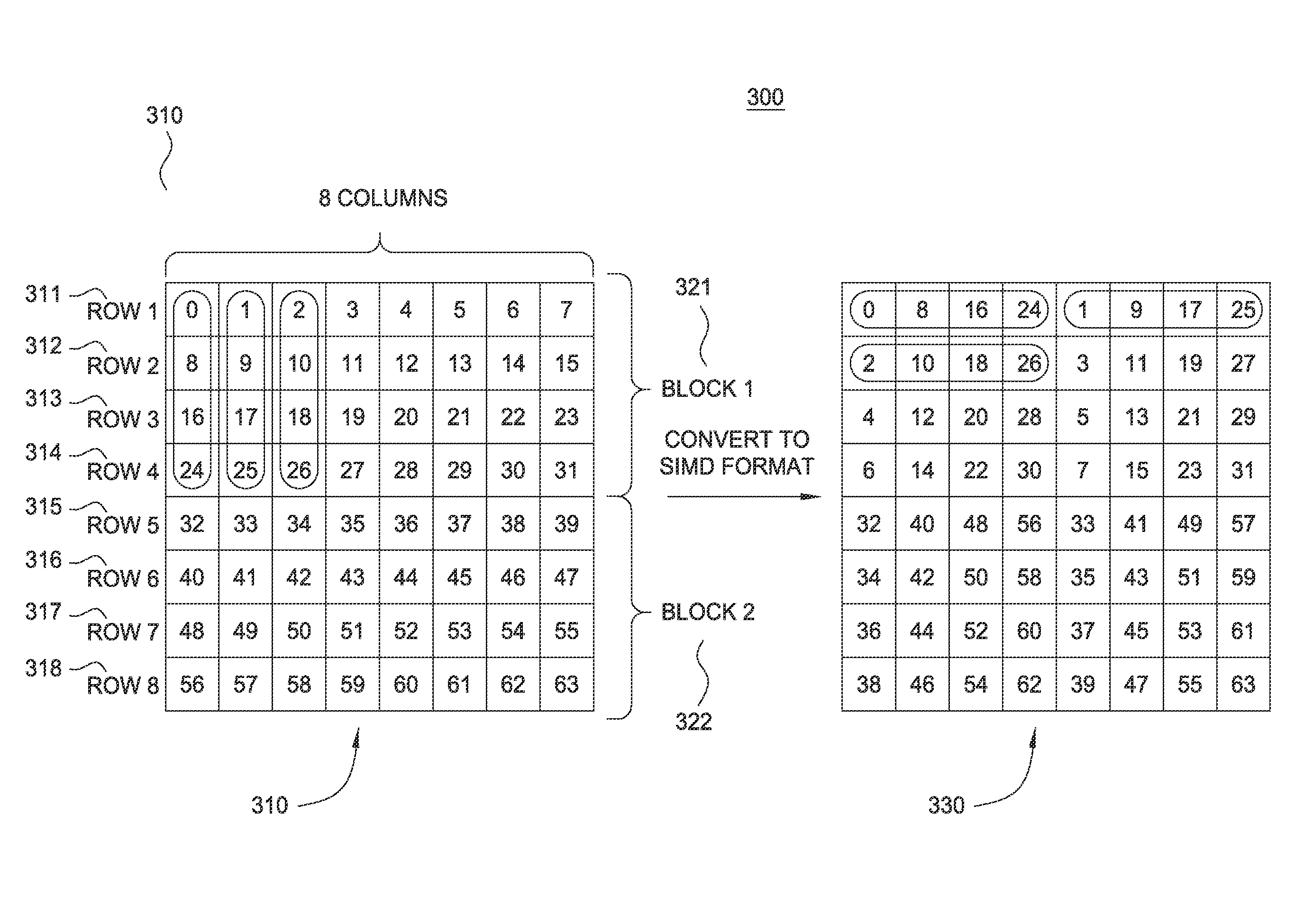
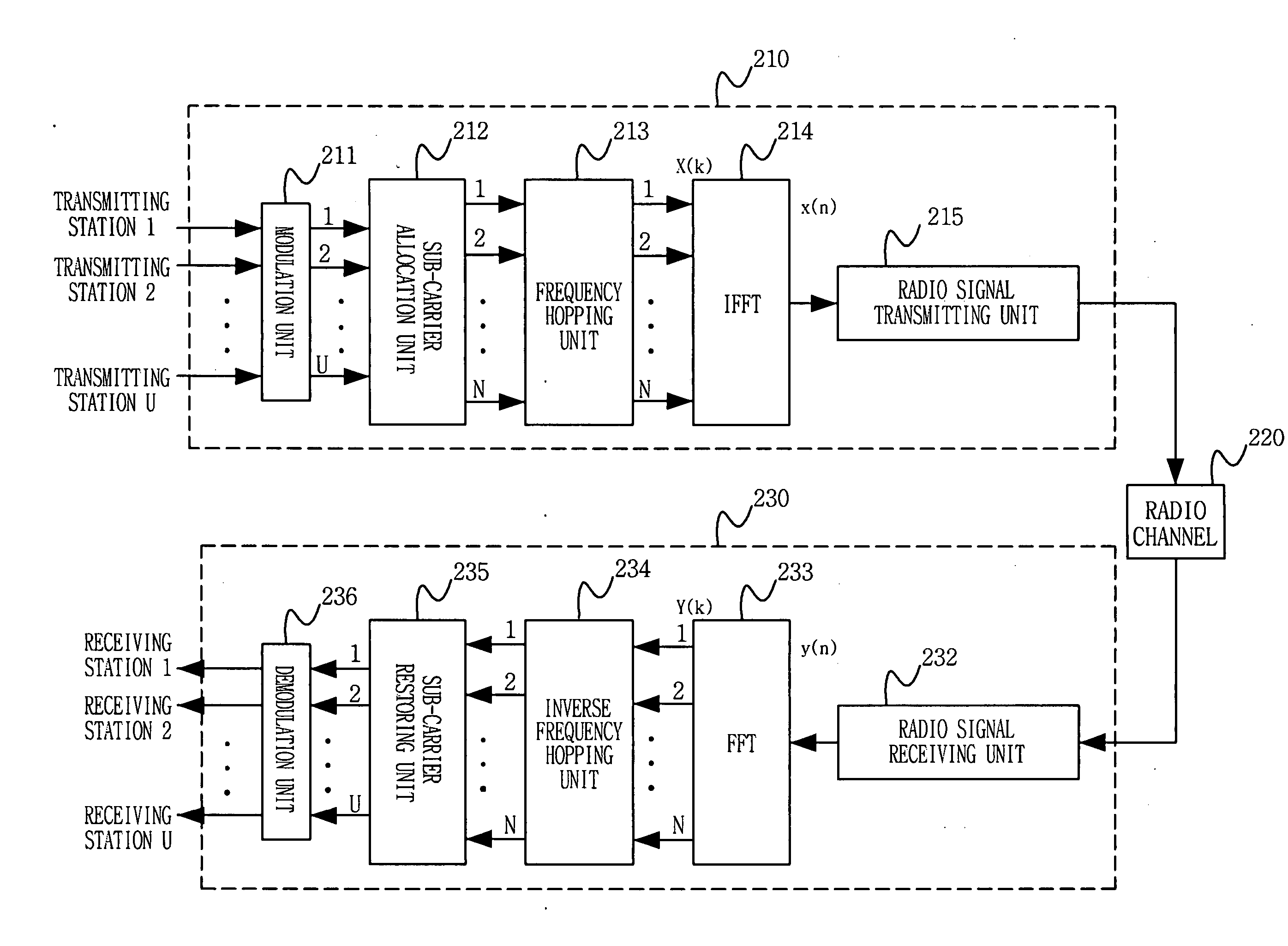
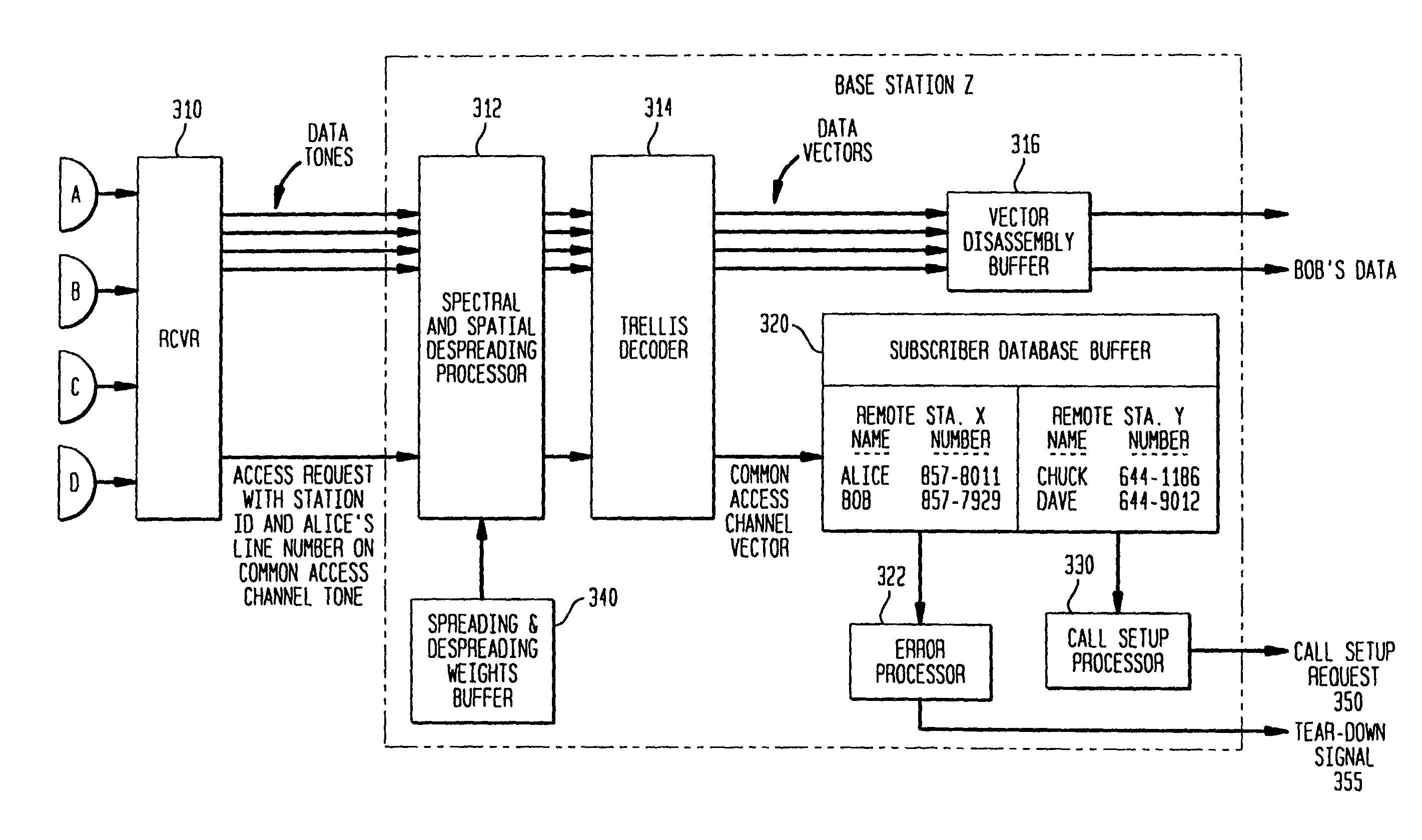
Processing array data on SIMD multi-core processor architectures
InactiveUS8484276B2Program control using stored programsGeneral purpose stored program computerFast Fourier transformFourier transform on finite groups
Owner:INT BUSINESS MASCH CORP
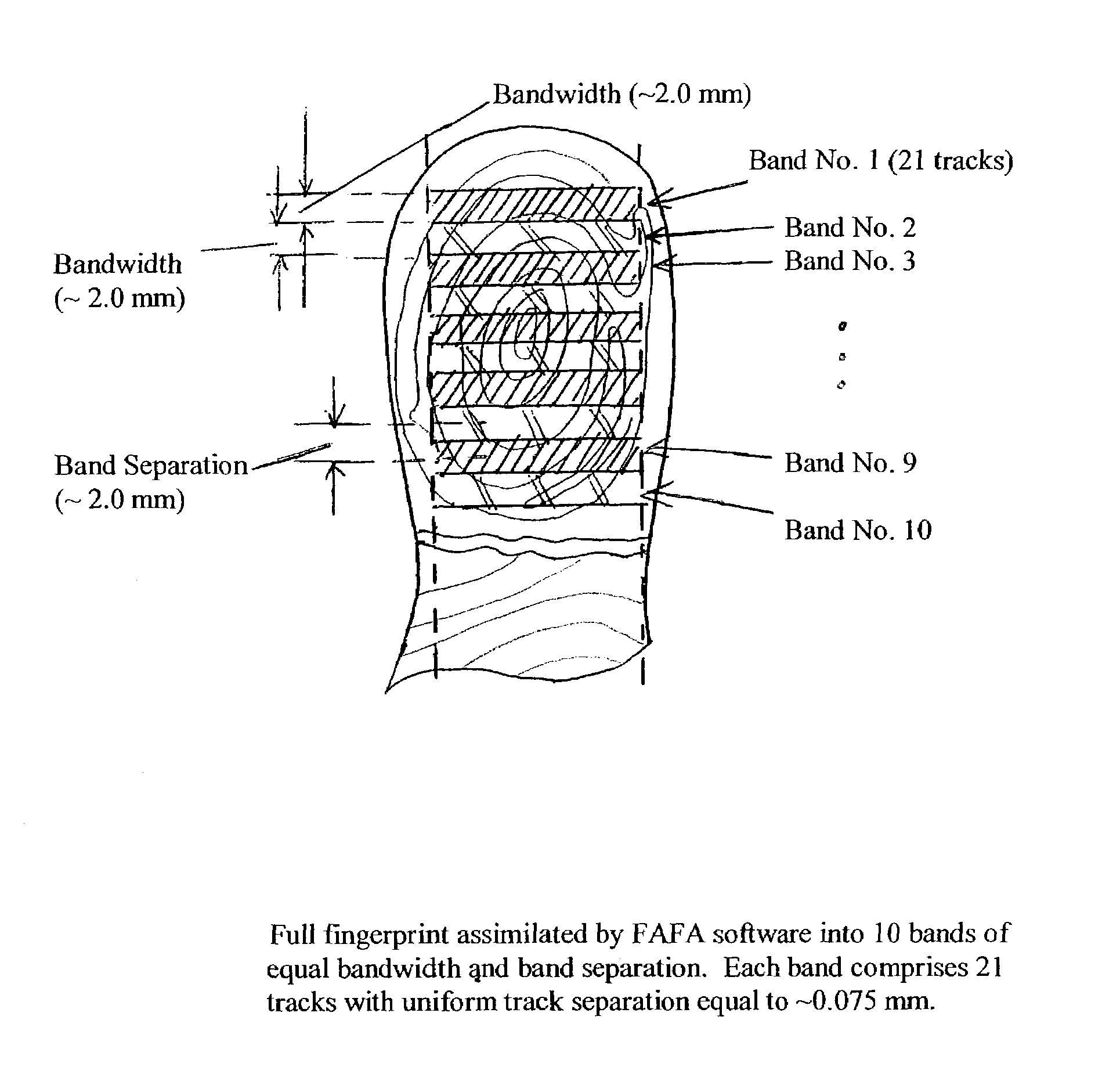
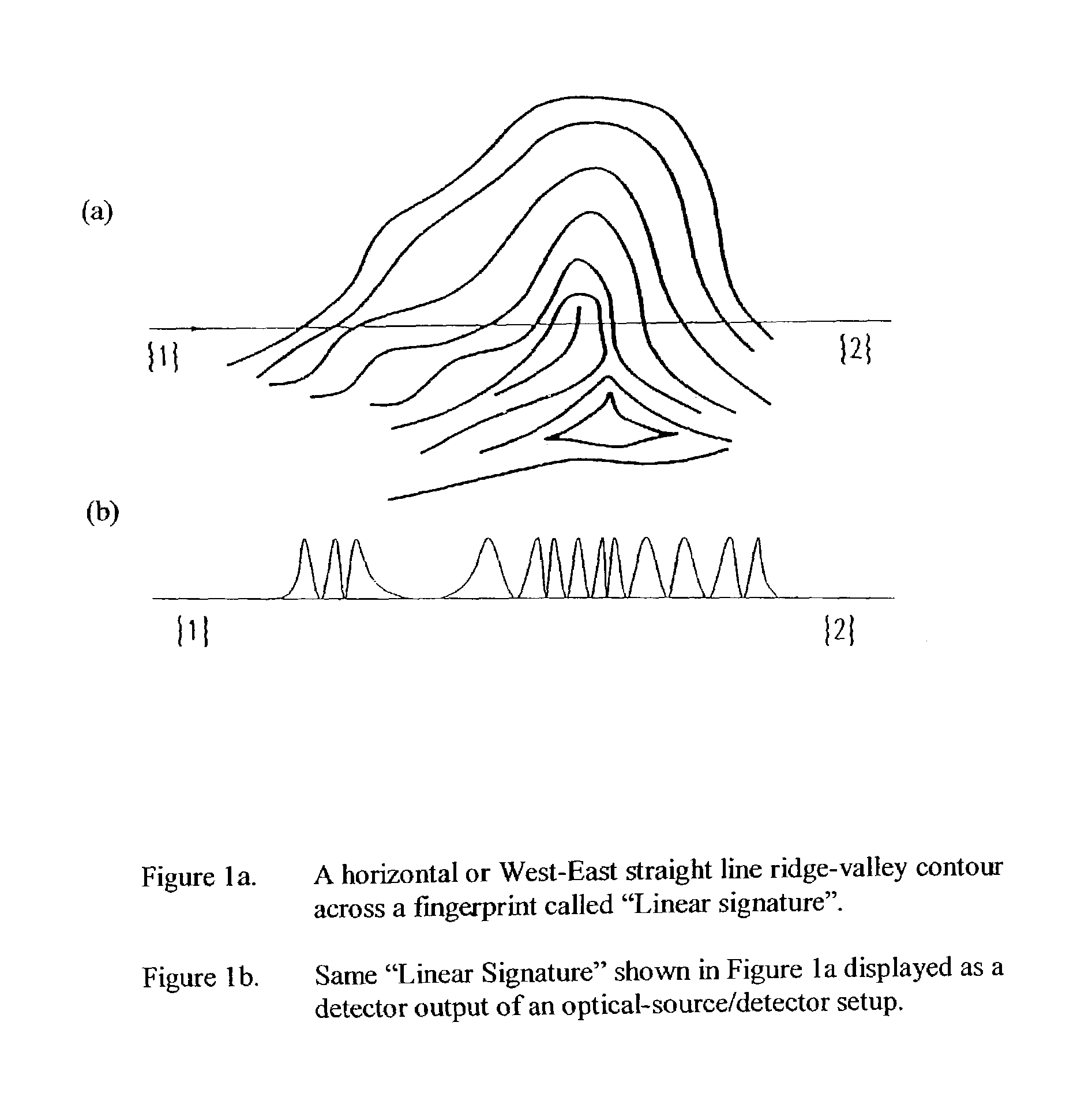
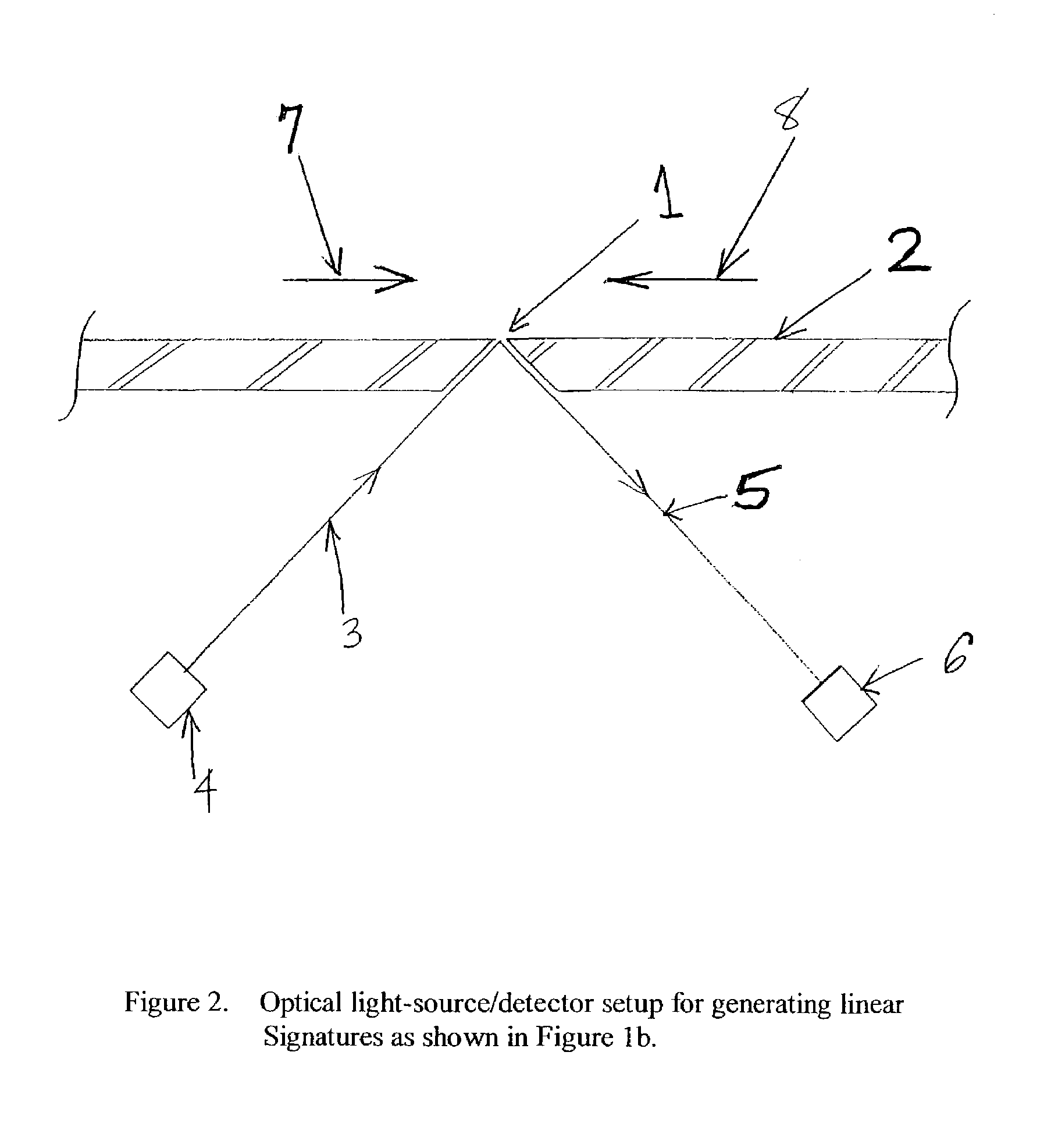
Method for authenticating an individual by use of fingerprint data
InactiveUS7136514B1Simple methodElectric signal transmission systemsImage analysisFast Fourier transformBiometrics
A method for authenticating an individual by use of fingerprint data that involves two different broad steps. The first step is to obtain a biometrics fingerprint signature template (“BFST”) for an individual in an enrollment process by selecting a plurality of bands for the BFST and obtaining a plurality of tracks corresponding to each of the plurality of bands by use of an enrollment frame of a selected finger of the individual, wherein the plurality of bands are spatially referenced to the enrollment frame and can be spatially referenced to a reference barrier. The second step is to authenticate (or not) a candidate finger against one or more BFST in an authentication process in which a swipe direction and an access code for the individual are selected, a plurality of candidate tracks are obtained from the candidate finger through use of the reference barrier in an authentication unit so that each of the plurality of candidate tracks is spatially referenced so as to be within a corresponding one of the plurality of bands, calculating a similarity index for each of the plurality of candidate tracks and each of the plurality of tracks for the band to which the candidate track corresponds by use of a Fast Fourier-transform fingerprint algorithm, and multiplying each maximum similarity index obtained for each of the plurality of candidate tracks to obtain a match index which indicates a match if it exceeds a preselected threshold.
Owner:WONG JACOB Y
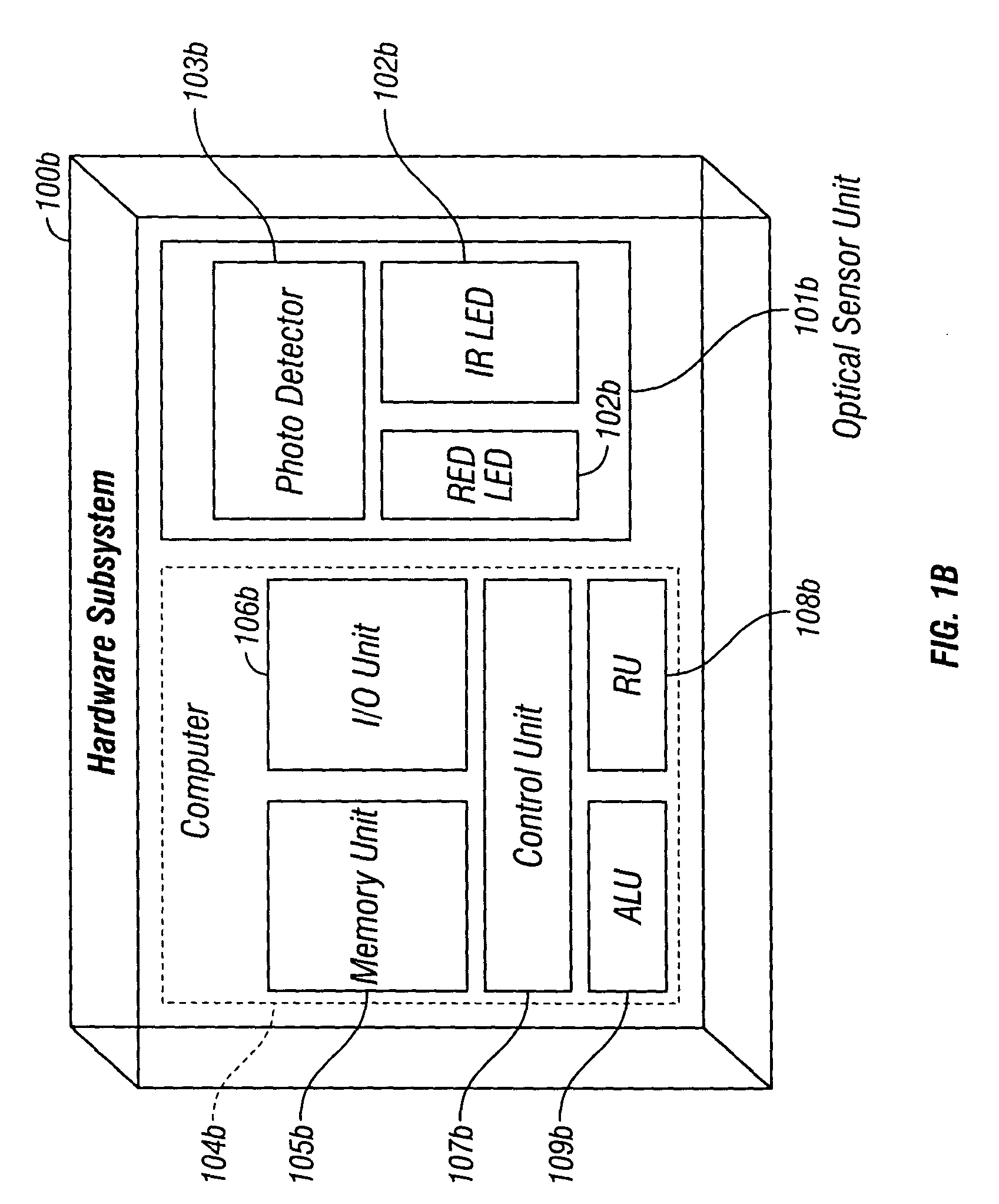
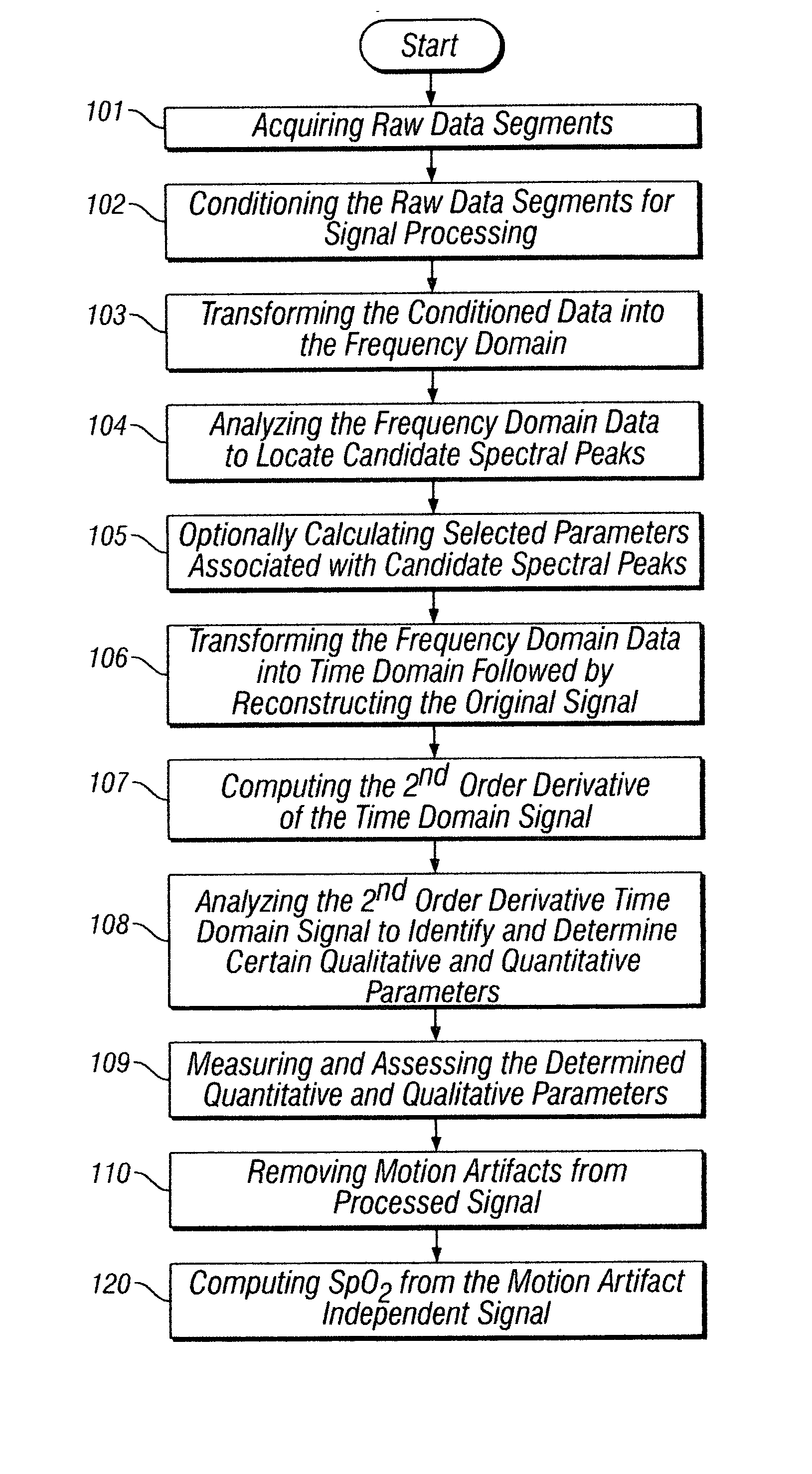
Separating motion from cardiac signals using second order derivative of the photo-plethysmogram and fast fourier transforms
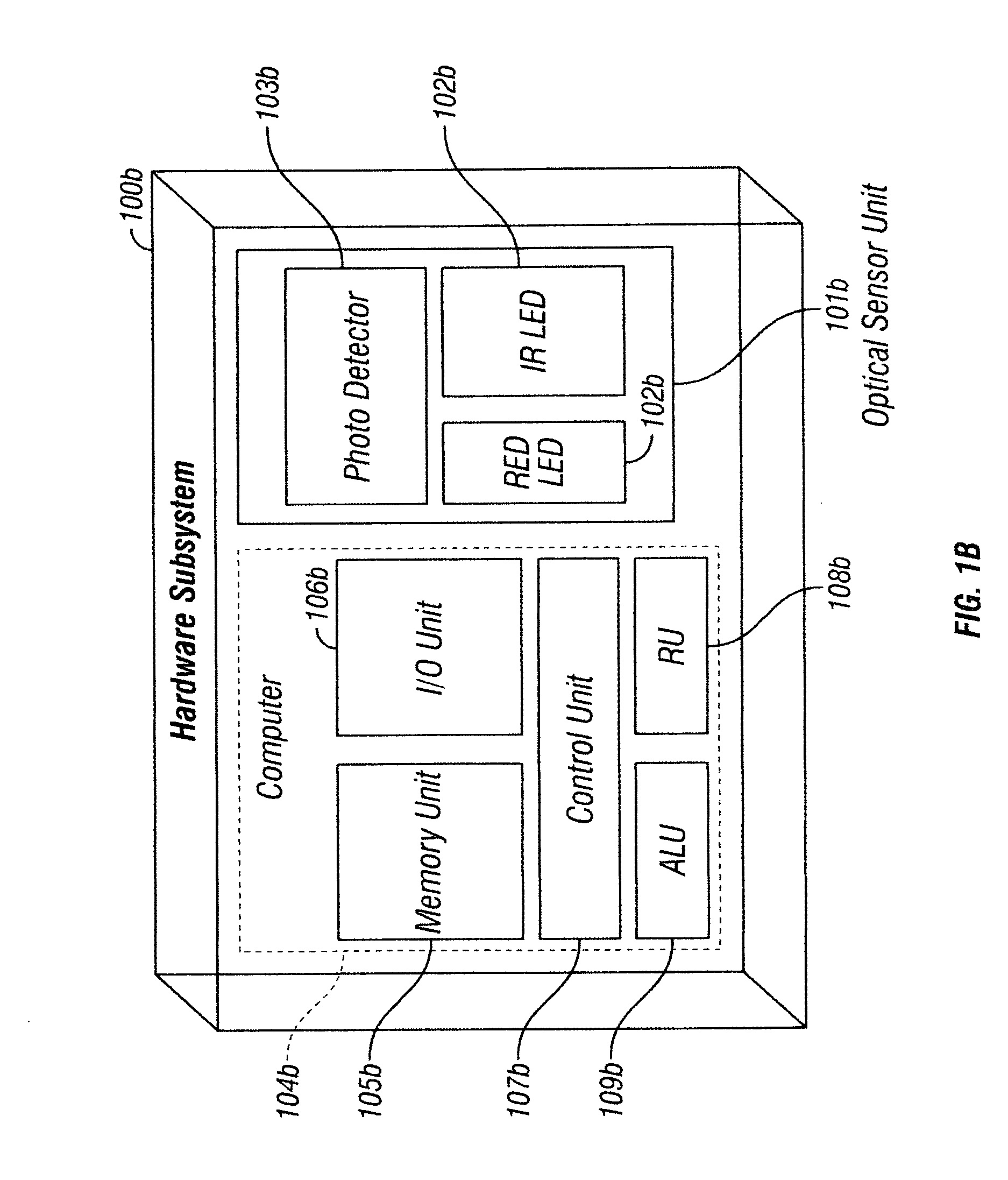
The present invention is directed toward a pulse oximetry system for the determination of a physiological parameter capable of removing motion artifacts from physiological signals comprises a hardware subsystem and a software subsystem. The software subsystem is used in conjunction with the hardware subsystem to perform a method for removing a plurality of motion artifacts from the photo-plethysmographic data and for obtaining a measure of at least one physiological parameter from the data. The method comprises acquiring the raw photo-plethysmographic data, transforming the data into the frequency domain, analyzing the transformed data to locate a series of candidate cardiac spectral peaks (primary plus harmonics), reconstructing a photo-plethysmographic signal in the time domain with only the candidate cardiac spectral peaks (primary plus harmonics), computing the second order derivative of the reconstructed photo-plethysmographic signal, analyzing the candidate second order derivative photo-plethysmographic signal to determine the absence or presence of cardiac physiologic signal characteristics, and finally selecting the best physiologic candidate from the series of potential cardiac spectral peaks (primary plus harmonics) based upon a second derivative scoring system. This scoring system is preferentially based upon second derivative processing analysis, but can be equally applied using the first, third, fourth or other similar derivative processing analysis.
Owner:SPACELABS HEALTHCARE LLC
Method and apparatus for enhancing noise-corrupted speech
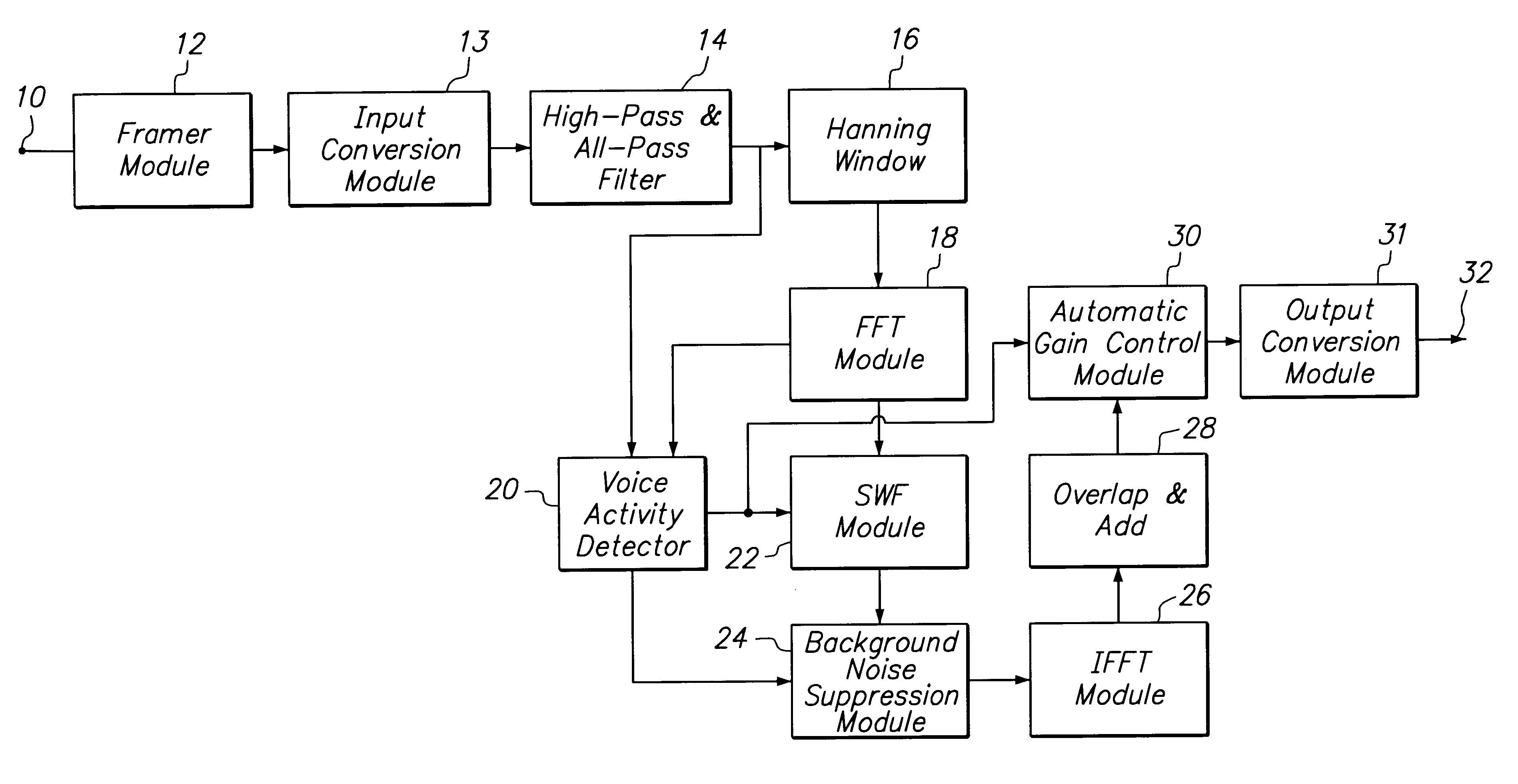
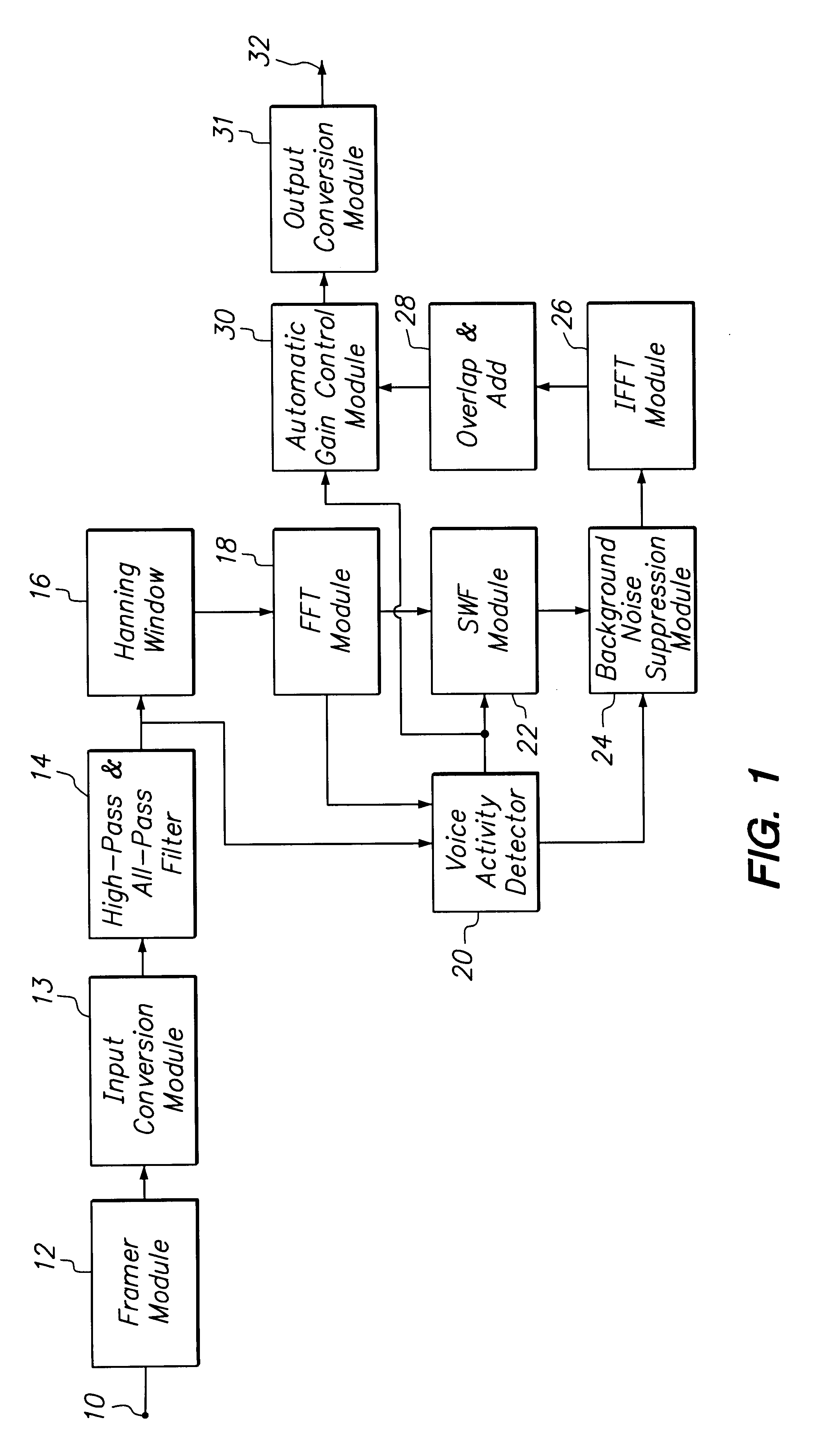
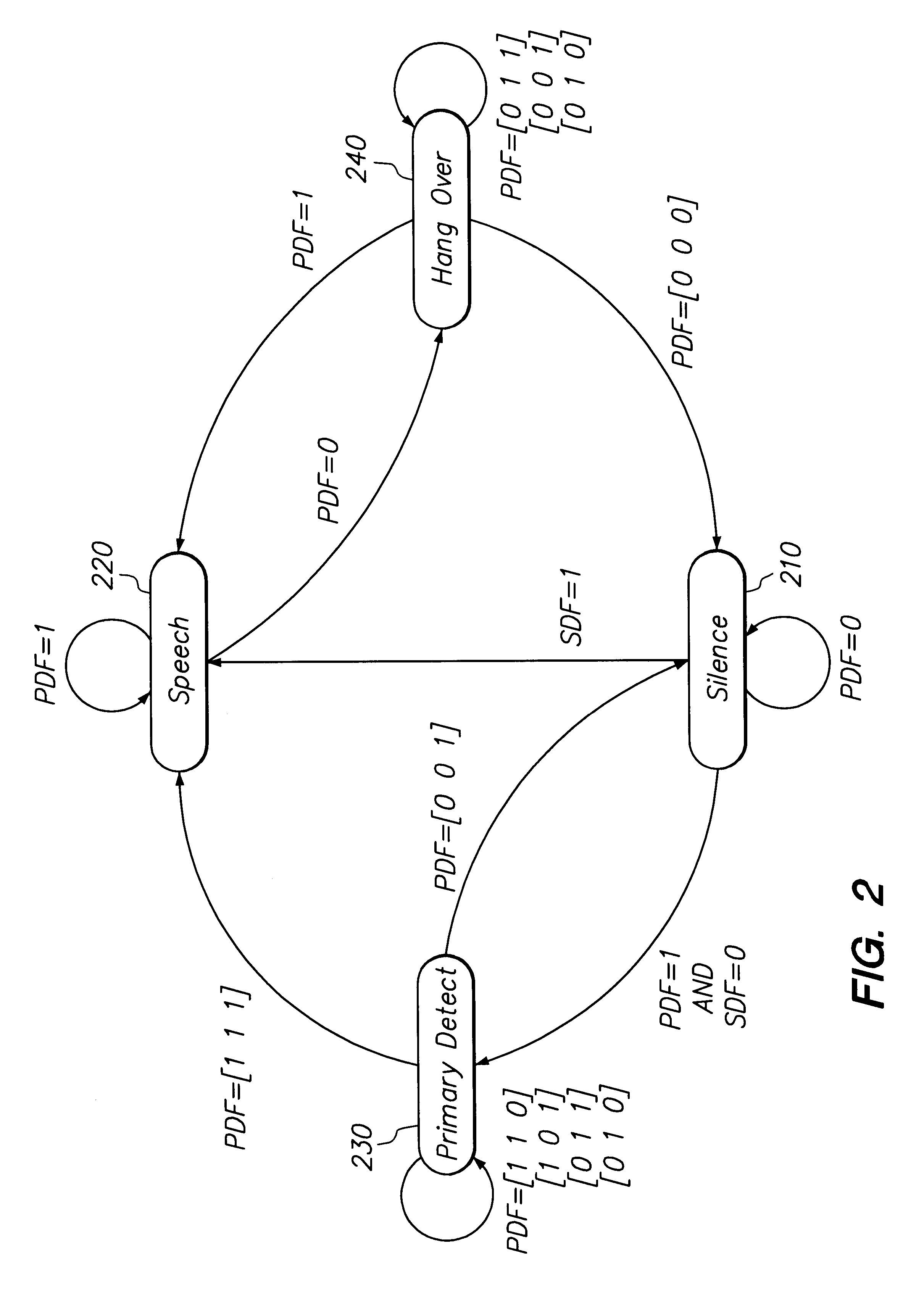
InactiveUS6415253B1Reduce peakImprove intelligibilitySpeech analysisTransmission noise suppressionTime domainFast Fourier transform
A noise suppression device receives data representative of a noise-corrupted signal which contains a speech signal and a noise signal, divides the received data into data frames, and then passes the data frames through a pre-filter to remove a dc-component and the minimum phase aspect of the noise-corrupted signal. The noise suppression device appends adjacent data frames to eliminate boundary discontinuities, and applies fast Fourier transform to the appended data frames. A voice activity detector of the noise suppression device determines if the noise-corrupted signal contains the speech signal based on components in the time domain and the frequency domain. A smoothed Wiener filter of the noise suppression device filters the data frames in the frequency domain using different sizes of a window based on the existence of the speech signal. Filter coefficients used for Wiener filter are smoothed before filtering. The noise suppression device modifies magnitude of the time domain data based on the voicing information outputted from the voice activity detector.
Owner:META C CORP
Method, apparatus and computer program product providing synchronization for OFDMA downlink signal
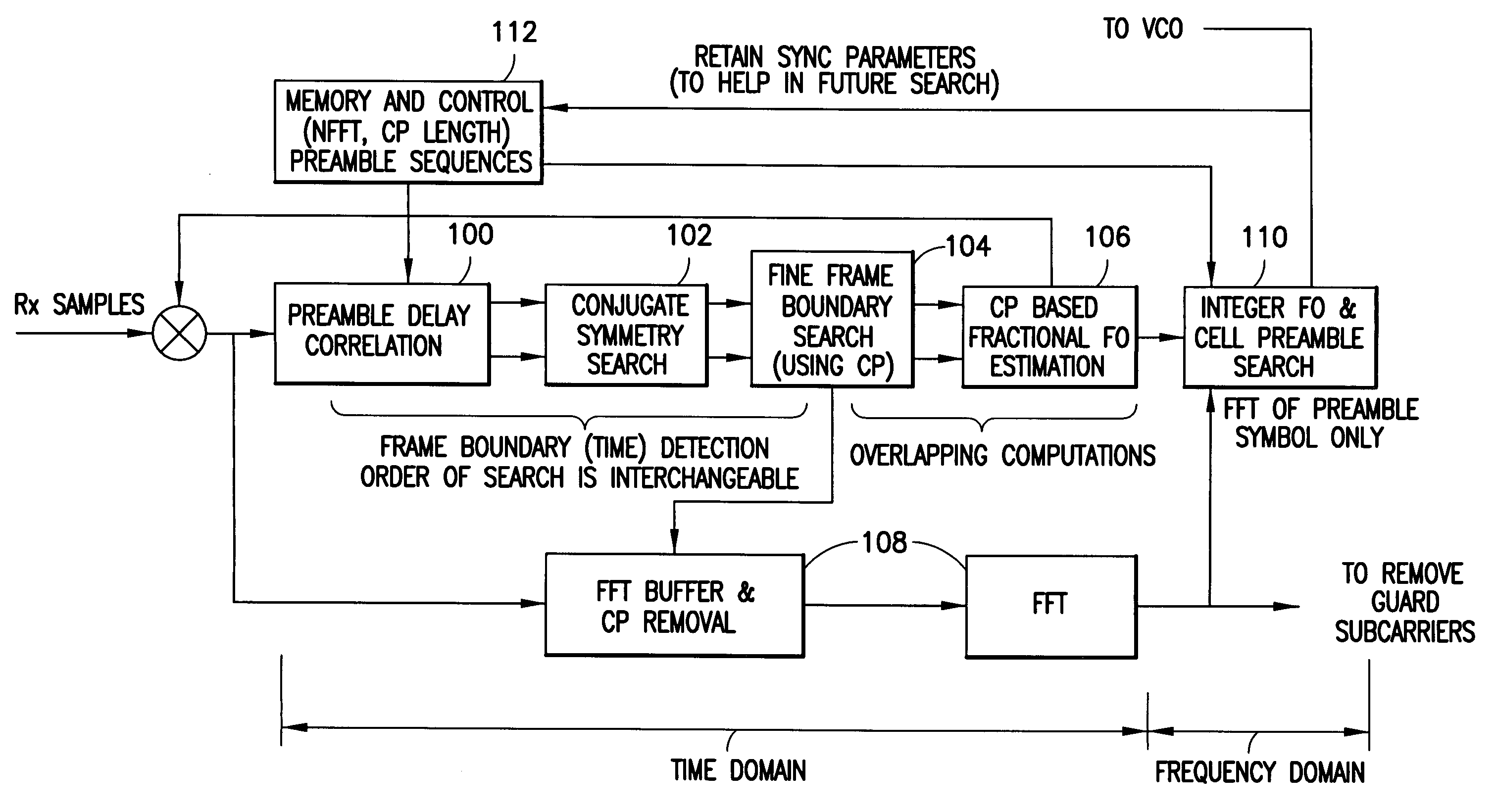
InactiveUS20070280098A1Good precisionModulated-carrier systemsTime-division multiplexCell specificCarrier frequency offset
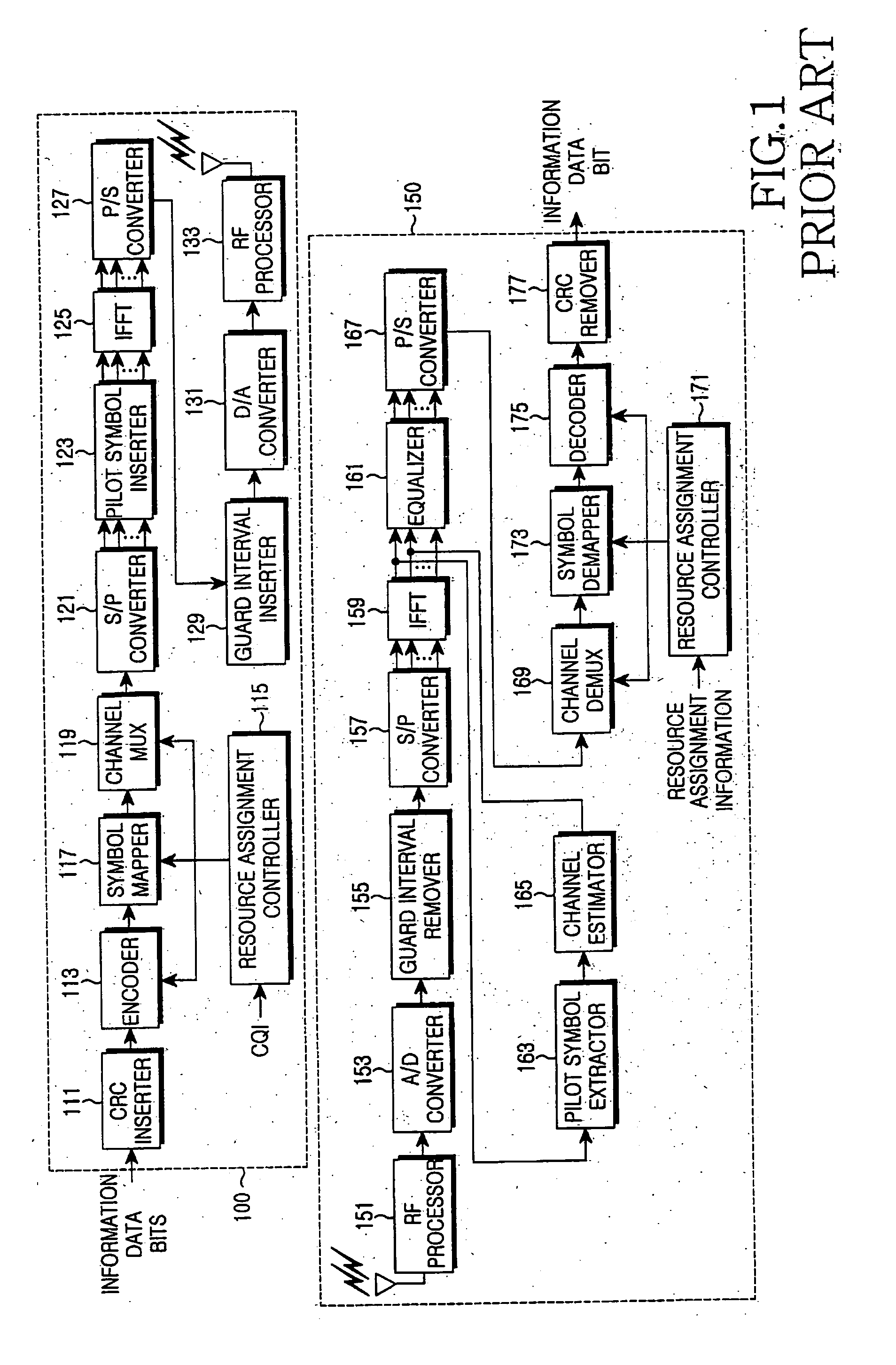
Disclosed is a method, a computer program product and a device that includes a receiver for receiving a downlink signal transmitted into a cell. The receiver is operable to obtain time, carrier frequency and cell-specific preamble synchronization to the received signal and includes a plurality of synchronization units that include a first detector to detect a frame boundary using preamble delay correlation; a second detector to detect the frame boundary with greater precision using a conjugate symmetry property over a region identified by the first detector; a cyclic prefix correlator to resolve symbol boundary repetition; an estimator, using the cyclic prefix, to estimate and correct a fractional carrier frequency offset; an operator to perform a Fast Fourier Transform of an identified preamble symbol and a frequency domain cross-correlator to identify cell-specific preamble sequences and an integer frequency offset in sub-carrier spacing. The transmitted signal may be a downlink signal transmitted into the cell from a base station that is compatible with IEEE 802.16e (WiMAX).
Owner:NOKIA TECHNOLOGLES OY
Methods for performing fast discrete curvelet transforms of data
ActiveUS20070038691A1The process is fast and accurateImprove representationComplex mathematical operationsDigital transformationFast Fourier transform
Fast digital implementations of the second generation curvelet transform for use in data processing are disclosed. One such digital transformation is based on unequally-spaced fast Fourier transforms (USFFT) while another is based on the wrapping of specially selected Fourier samples. Both digital transformations return a table of digital curvelet coefficients indexed by a scale parameter, an orientation parameter, and a spatial location parameter. Both implementations are fast in the sense that they run in about O(n2 log n) flops for n by n Cartesian arrays or about O(N log N) flops for Cartesian arrays of size N=n3; in addition, they are also invertible, with rapid inversion algorithms of about the same complexity.
Owner:CALIFORNIA INST OF TECH +1
Apparatus and method for transmitting and receiving side information of a partial transmit sequence in an OFDM communication system
ActiveUS7376074B2Minimizing PAPRFrequency-division multiplexCode division multiplexNonlinear distortionData stream
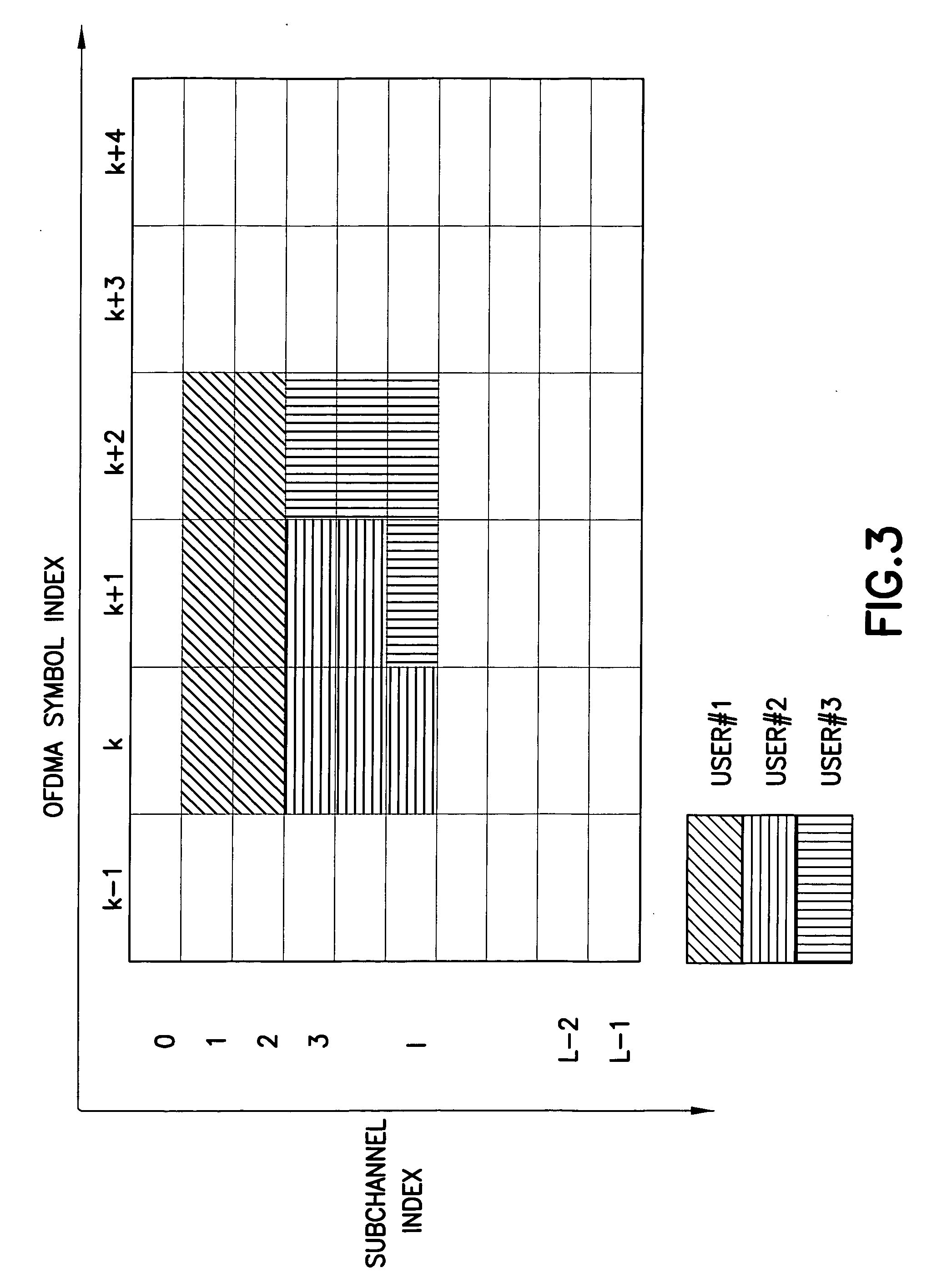
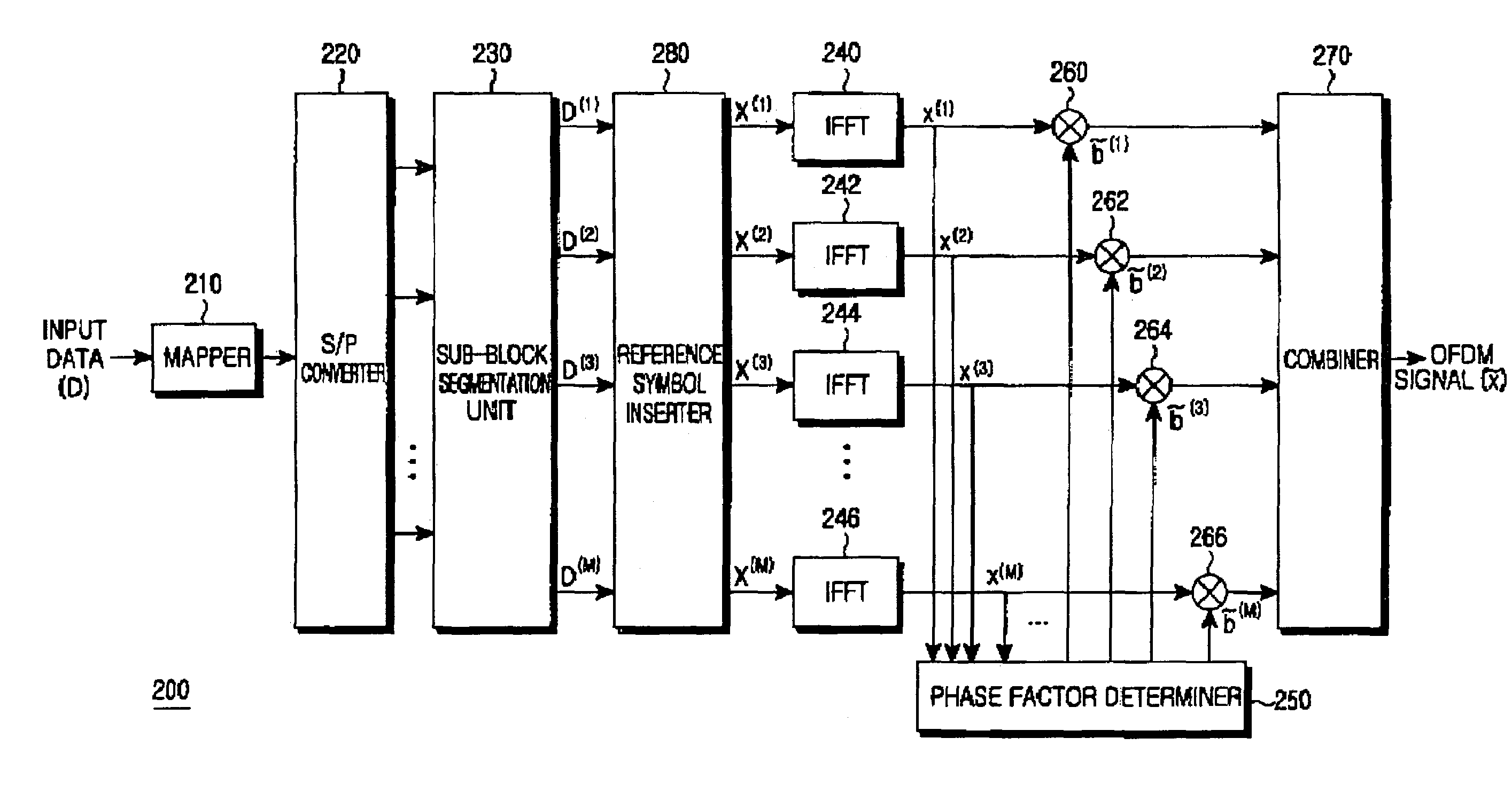
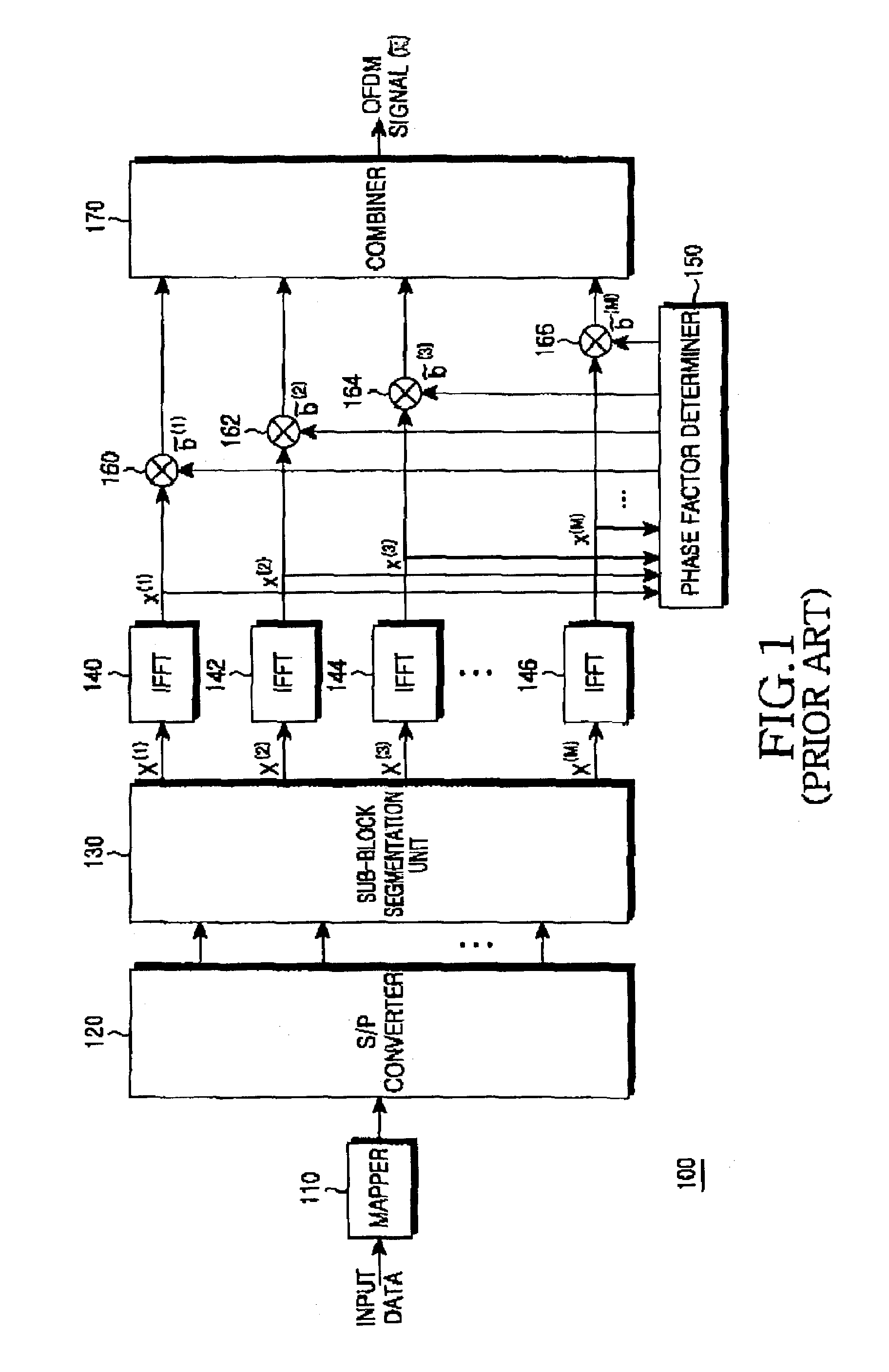
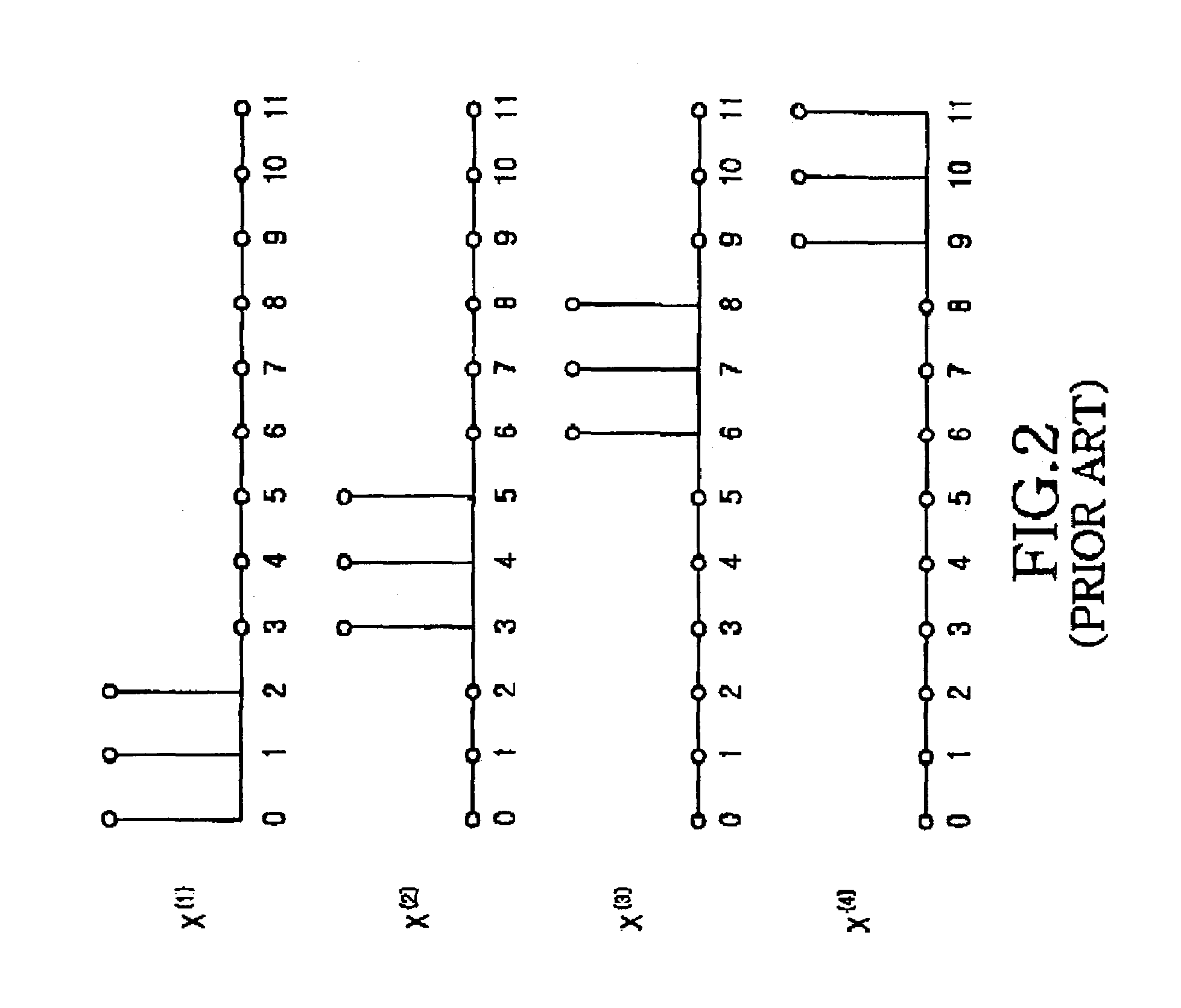
An OFDM (Orthogonal Frequency Division Multiplexing) communication system that multiplexes data with a plurality of orthogonal sub-carrier frequencies, which includes a transmitter for converting a serial data stream into parallel data, and segmenting the parallel data into a plurality of blocks having a plurality of data blocks; inserting reference data having information representing a phase value and a position into which the reference symbol is inserted, into each of the segmented blocks; IFFT (Inverse Fast Fourier Transform)-transforming the respective blocks into time-based signals where sub-carrier frequencies are separately assigned to the data blocks; and determining phase factors of the IFFT-transformed time-based signals to reduce a peak-to-average power ratio (PAPR) where non-linear distortion occurs due to coincidence of phases of the data blocks IFFT-transformed with the sub-carrier frequencies, and phase-rotating the IFFT-transformed signals according to the determined phase factors before transmission.
Owner:SAMSUNG ELECTRONICS CO LTD
Apparatus and method for transmitting/receiving uplink random access channel in mobile communication system
InactiveUS20050286409A1Improve performanceGood estimateModulated-carrier systemsTransmission path divisionFast Fourier transformRandom-access channel
An apparatus and method for transmitting / receiving an random access channel (RACH) signal in a broadband wireless communication system where a total uplink frequency band is divided into M sub-bands are provided. In the RACH transmitting apparatus, a generator generates an access code. A sub-carrier allocator divides the access code into M sub-blocks and allocates each of the M sub-blocks to successive sub-carriers in a sub-band. An inverse fast Fourier transform (IFFT) processor generates an orthogonal frequency division multiplexing (OFDM) symbol by performing an IFFT on the allocated sub-blocks.
Owner:SAMSUNG ELECTRONICS CO LTD
Methods and apparatus for reducing signal degradation
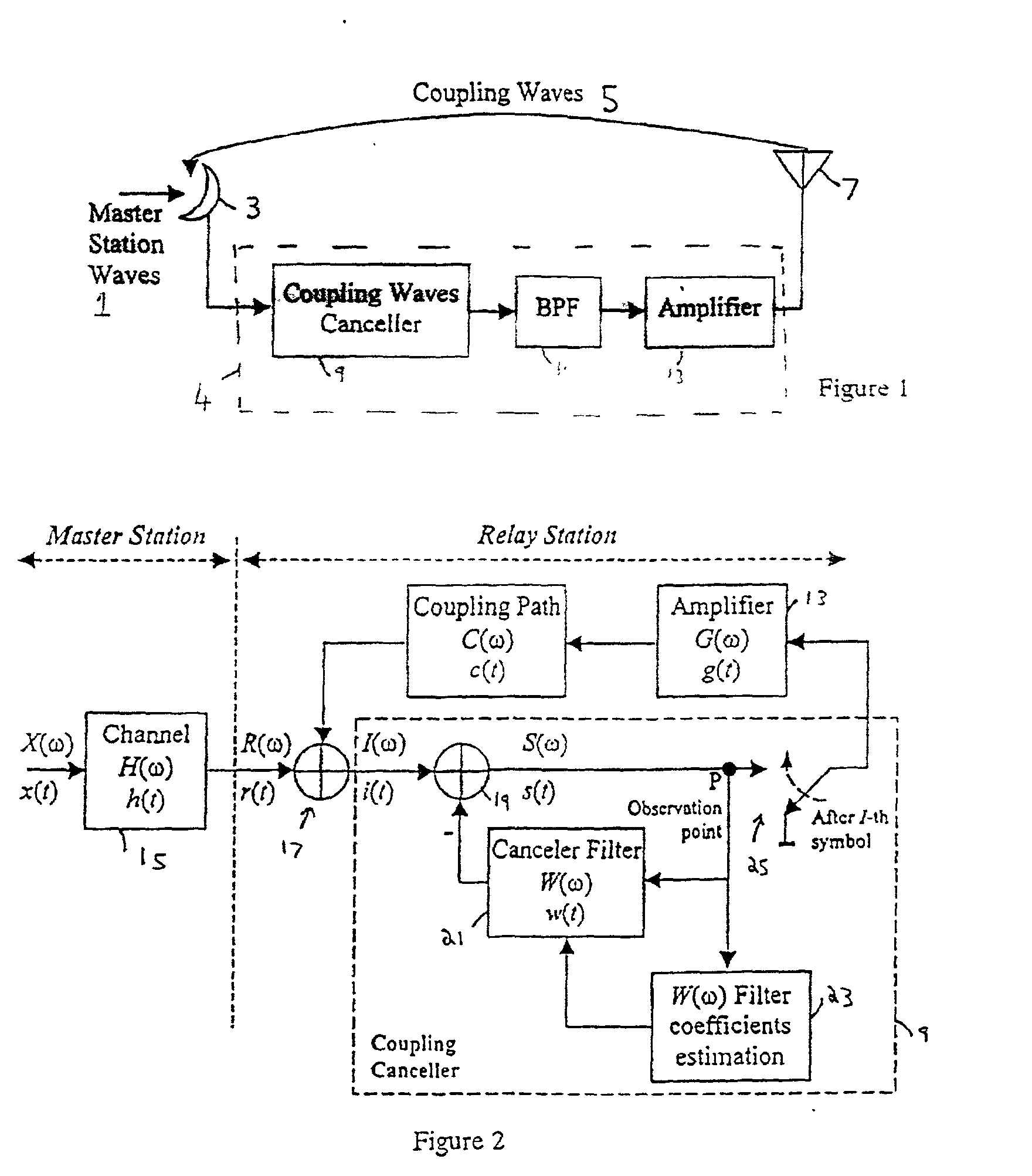
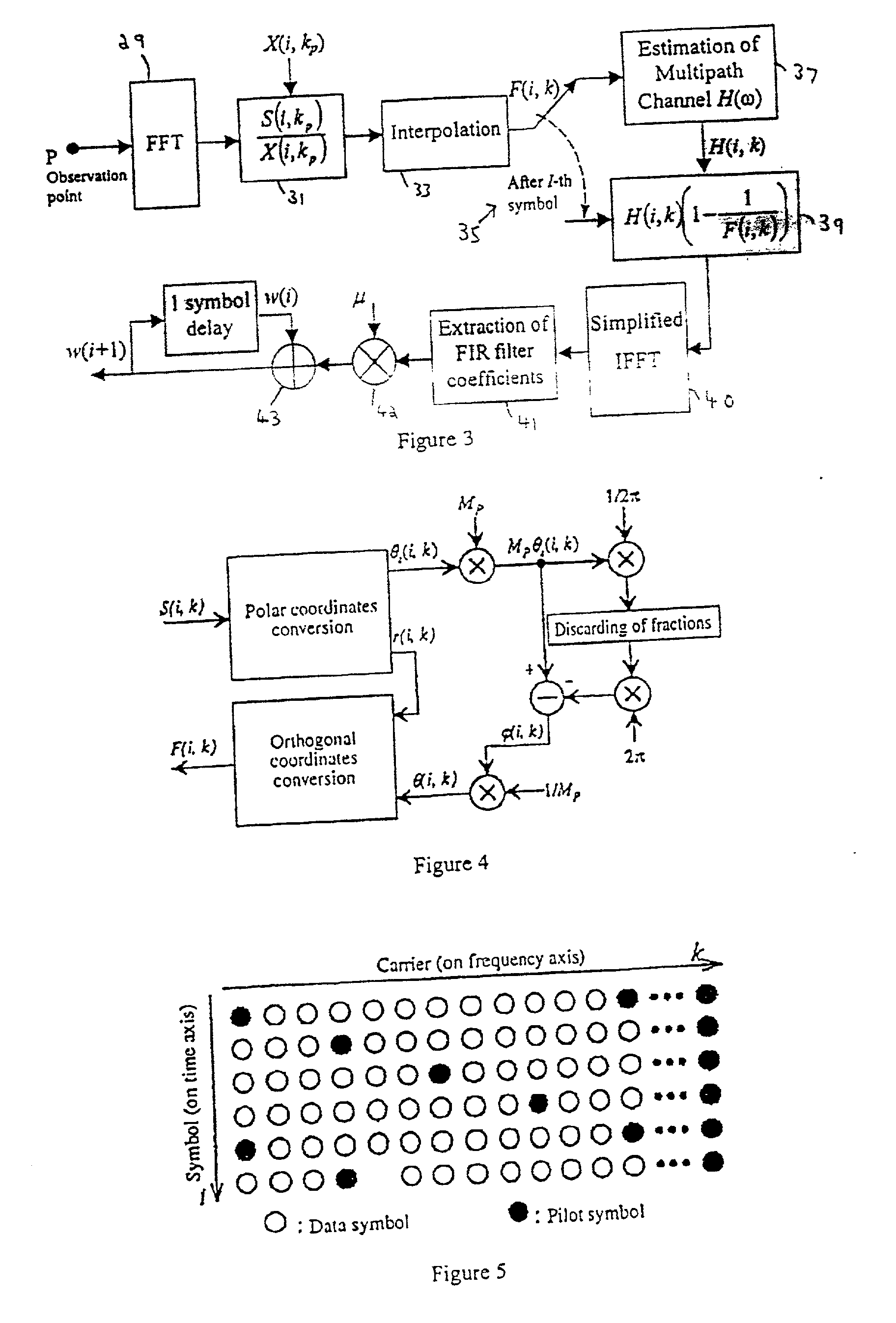
ActiveUS20020039383A1Error minimizationReduce the differencePulse transformerAdaptive networkFast Fourier transformMultipath interference
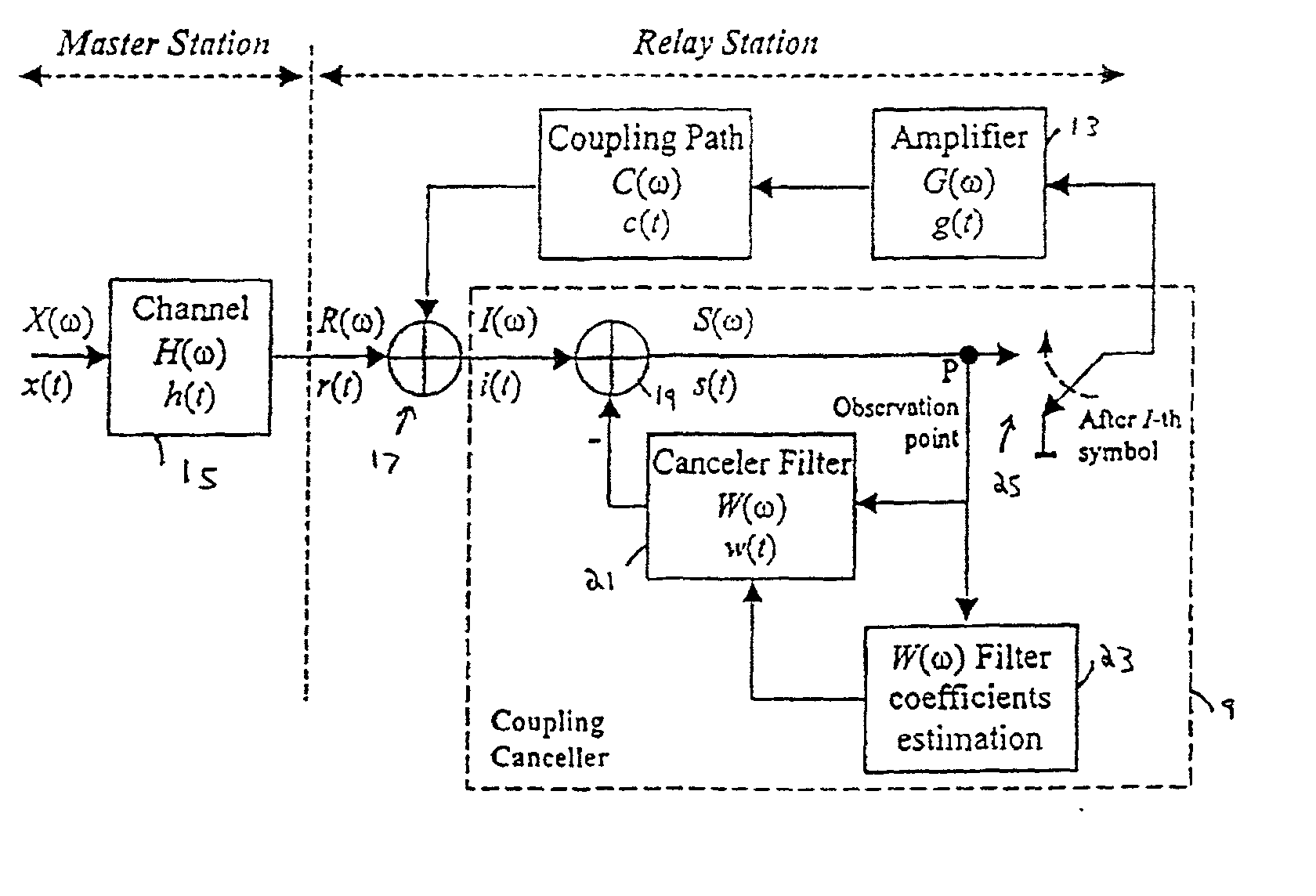
A single frequency relay station receives a signal from a master station, and retransmits it. Before retransmitting the signal, the relay station uses a digital filter to subtract from the signal components which arise from multipath interference and coupling interference. The coefficients used by the digital filter are derived from characteristics of the multipath interference and the overall transfer function of the relay station. These are derived by turning off the retransmission, so that the multipath interference can be estimated from the received signal, and commencing the retransmission again, to determine the transfer function. A simplified inverse fast Fourier transform is used to simplify the calculations.
Owner:WIPRO LTD
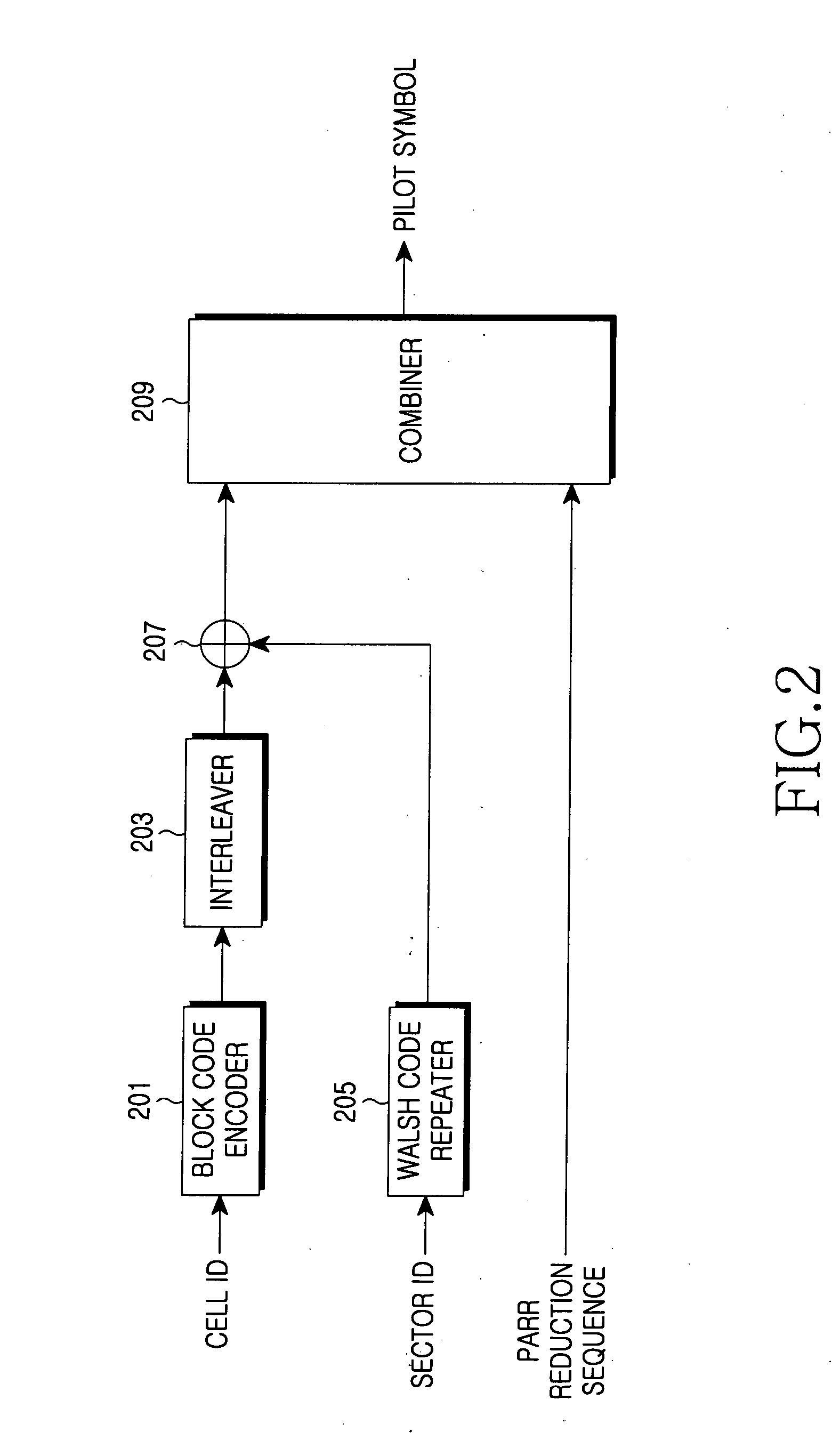
Apparatus and method for transmitting/receiving pilot signal in communication system using OFDM scheme
ActiveUS20060028976A1Interference minimizationMinimize interferenceModulated-carrier systemsRadio transmissionComputer hardwareFast Fourier transform
Disclosed is a method for transmitting a reference signal for identification of each cell in a communication system including a plurality of cells each of which is identified by a cell identifier. The method includes receiving a cell identifier, and generating a block code corresponding to the cell identifier using a predetermined block code generator matrix, and generating a first part sequence using the block code; selecting a second part sequence in accordance with the cell identifier; generating a reference signal of a frequency domain using the first part sequence and the second part sequence; converting the reference signal of the frequency domain to a reference signal of a time domain through an Inverse Fast Fourier Transform operation and transmitting the reference signal of the time domain in a predetermined reference signal transmission interval.
Owner:NOKIA TECHNOLOGLES OY
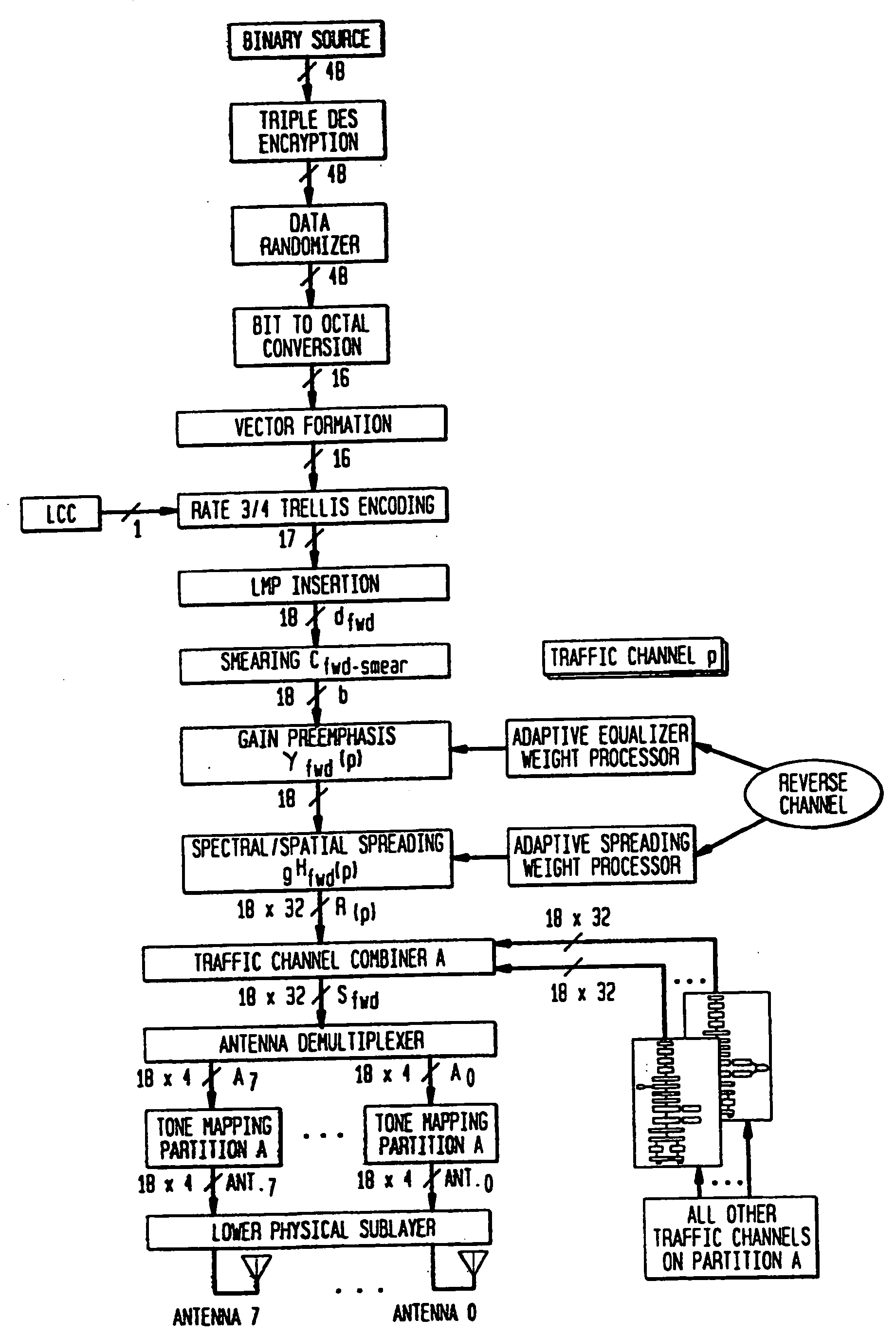
Highly bandwidth-efficient communications
InactiveUS20060193373A1Reduce distractionsSimple calculationSpatial transmit diversityTransmission control/equalisingFrequency spectrumCarrier signal
A discrete multitone stacked-carrier spread spectrum communication method is based on frequency domain spreading including multiplication of a baseband signal by a set of superimposed, or stacked, complex sinusoid carrier waves. In a preferred embodiment, the spreading involves energizing the bins of a large Fast Fourier transform (FFT). This provides a considerable savings in computational complexity for moderate output FFT sizes. Point-to-multipoint and multipoint-to-multipoint (nodeless) network topologies are possible. A code-nulling method is included for interference cancellation and enhanced signal separation by exploiting the spectral diversity of the various sources. The basic method may be extended to include multielement antenna array nulling methods for interference cancellation and enhanced signal separation using spatial separation. Such methods permit directive and retrodirective transmission systems that adapt or can be adapted to the radio environment. Such systems are compatible with bandwidth-on-demand and higher-order modulation formats and use advanced adaptation algorithms. In a specific embodiment the spectral and spatial components of the adaptive weights are calculated in a unified operation based on the mathematical analogy between the spectral and spatial descriptions of the airlink.
Owner:CINGULAR WIRELESS II LLC
Frequency hopping ofdma method using symbols of comb pattern
InactiveUS20060072649A1Reduce the amount requiredTransmission path divisionPicture reproducers using cathode ray tubesTime domainFast Fourier transform
Method for providing frequency-hopping OFDMA using symbols of comb patter, the method including the steps of: a) assigning frequency domain signal X(k) of comb pattern (comb symbol, k is frequency index) to modulated data sequence, the comb symbol comprising predetermined number of sub carriers (sub carrier group) which are placed with predetermined interval in the whole available frequency band; b) getting the comb symbol hopped for the comb symbol to have independent frequency offset; and c) inverse fast fourier transforming the comb symbol to time domain signal x(n) (n is time index) and transmitting the signal.
Owner:ELECTRONICS & TELECOMM RES INST
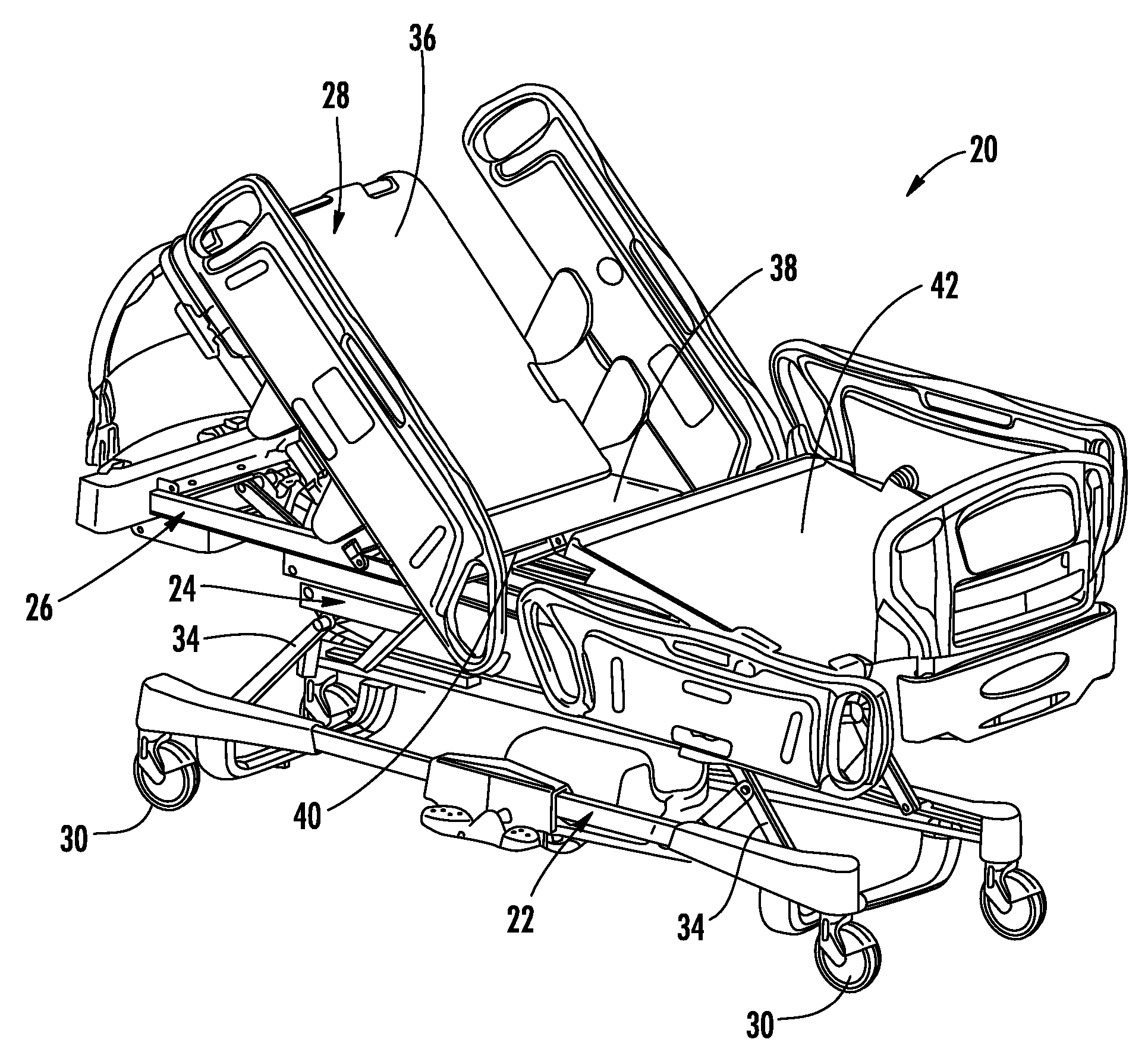
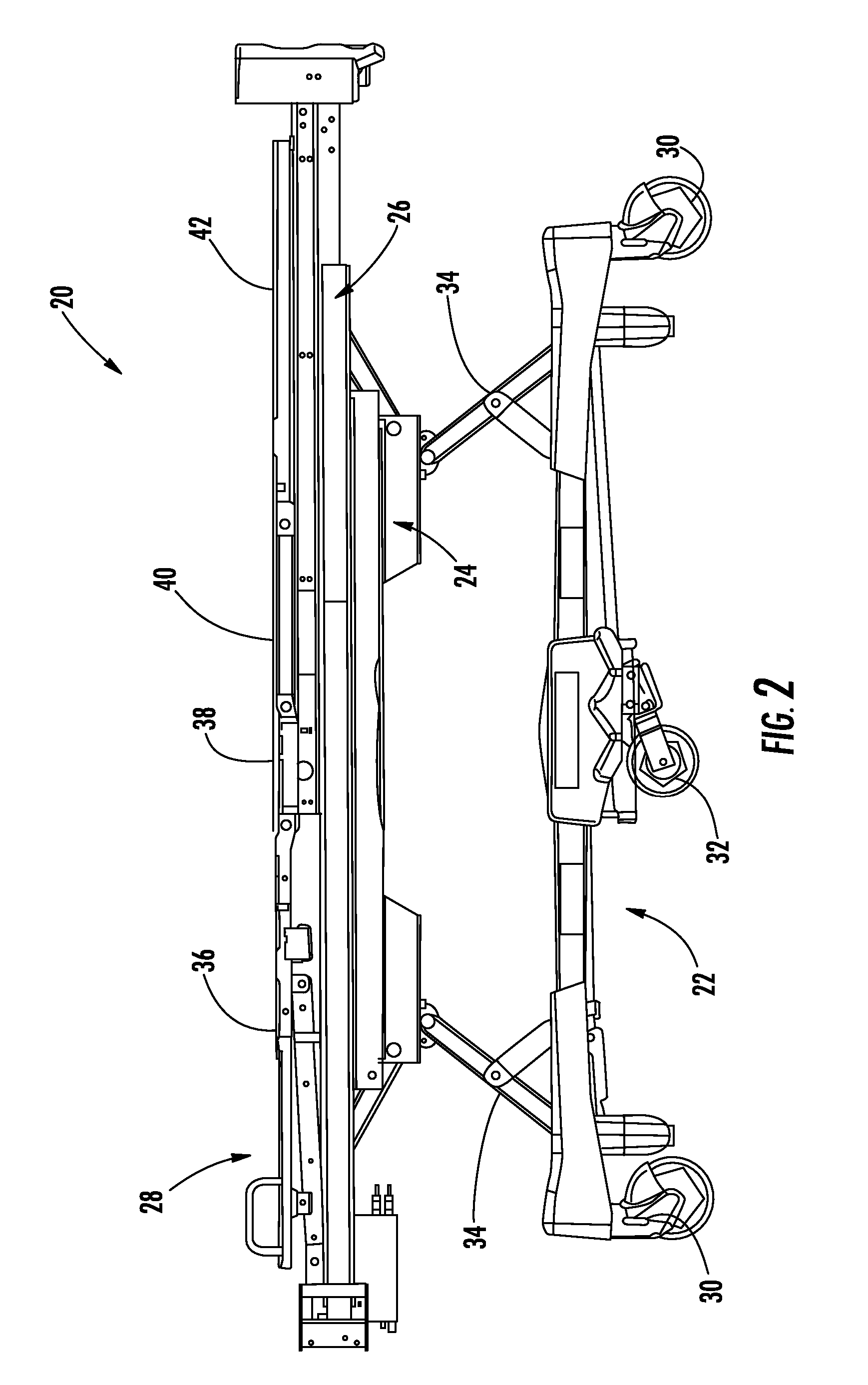
System for detecting and monitoring vital signs
ActiveUS20080005838A1Simple systemCatheterRespiratory organ evaluationFast Fourier transformPhysical therapy
A system and method for determining and monitoring various characteristics of a patient positioned on a patient support apparatus, such as a bed, stretcher, or cot, is disclosed. The system and method involve monitoring the forces exerted by the patient on one or more force sensors, which may be load cells on the support apparatus. These force sensors will detect vibrations that correspond to various conditions of the patient, including the patient's heart rate, breathing rate, and / or the seizure status of a patient. These vibrations may be analyzed, such as by Fast Fourier Transforms, in order to determine the various conditions of the patient.
Owner:STRYKER CORP
Apparatus and method for transmitting/receiving pilot signals in an OFDM communication system
InactiveUS20050094550A1Maximizing a carrier to interference noise ratioMinimize overheadTransmission path divisionMulti-frequency code systemsFast Fourier transformCommunications system
A radio communication system divides an entire frequency band into a plurality of subcarrier bands, forms a symbol with signals on the subcarrier bands, forms a frame with a plurality of symbols, transmits a pilot signal within symbols in a predetermined position of the frame, and transmits a data signal within symbols other than the symbols for transmitting the pilot signal. A transmitter allocates subcarriers through which the reference signal is transmitted, wherein the subcarriers are allocated to have an exclusive relation with subcarriers through which reference signals of other transmitters are transmitted, generates the pilot signal, performs an inverse fast Fourier transform (IFFT) on the pilot signal by applying an IFFT size which is less than or equal to an IFFT size applied to the data signal, and transmits the IFFT-processed reference signal to a receiver.
Owner:SAMSUNG ELECTRONICS CO LTD
Method and apparatus for coexistence
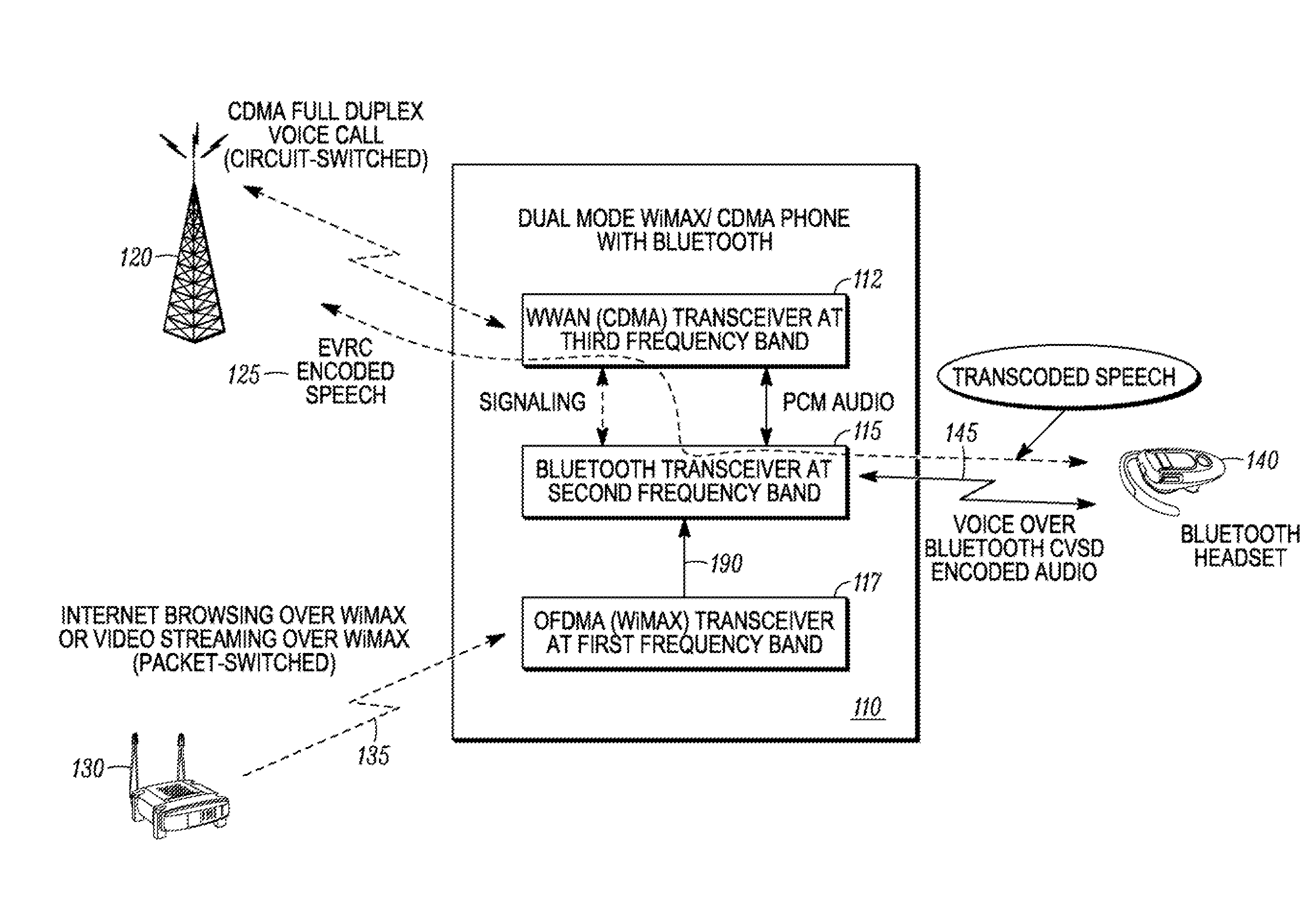
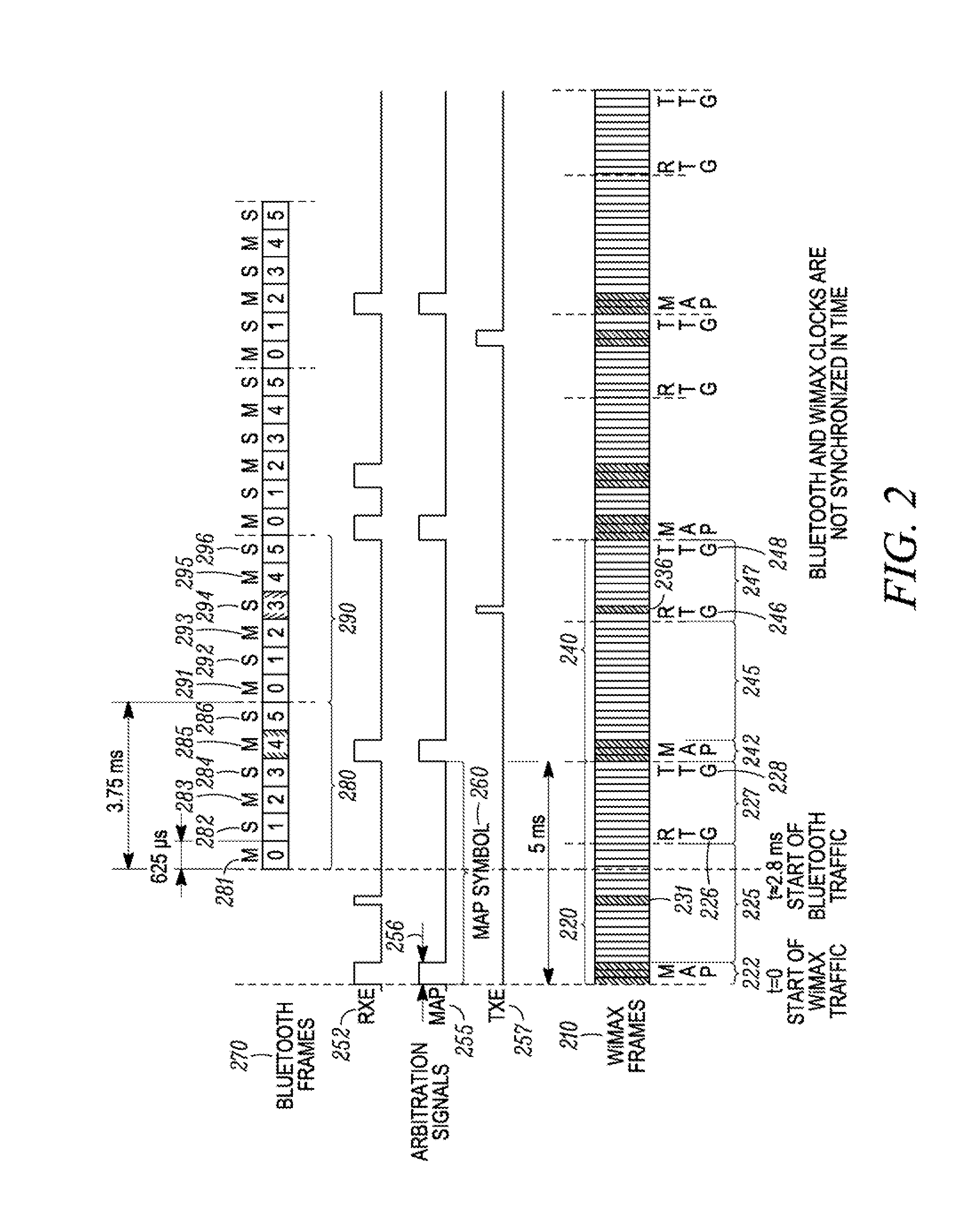
A method for coexistence of an orthogonal frequency division multiple access (OFDMA) receiver (117) such as a WiMAX receiver with a synchronous frame-based transmitter (115) such as a Bluetooth transmitter within a mobile station (110) receives an estimated media access protocol (MAP′) signal indicating when a MAP message is expected to be received by the OFDMA receiver (117) and uses it at a Bluetooth shutdown signal (190) at least when a MAP message is expected to be received. The MAP′ signal can be taken directly from the ODFMA transceiver (117) or it may be produced through analysis of a receiver-enable (RXE) signal that includes not only MAP symbols but also downlink data symbols. The RXE signal can be analyzed using interrupt-and-timer, Fast Fourier Transform, covariance, and / or delay-locked loop techniques to extract historical MAP symbol information and generate expected MAP symbol information. Shutting down a Bluetooth transmitter during expected MAP message receipt permits the OFDMA receiver to maintain synchronicity with an access point while not requiring the Bluetooth transmitter to shut down every time the OFDMA receiver expects to receive an OFDMA symbol.
Owner:GOOGLE TECH HLDG LLC
Method and apparatus for transmitting uplink acknowledgement information in an OFDMA communication system
ActiveUS20050286402A1Guaranteed normal transmissionImprove reliabilityError prevention/detection by using return channelTransmission path divisionFast Fourier transformCommunications system
A method and apparatus for transmitting uplink acknowledge information (ACK) in a communication system using an orthogonal frequency division multiple access (OFDMA) scheme. The method includes receiving a data bit for the uplink ACK; outputting codewords corresponding to the data bit; performing quadrature phase shift keying (QPSK) modulation on symbols for ACK vector indexes corresponding to the codewords for the received data bit; performing inverse fast Fourier transform (IFFT) on a transmission signal having subcarrier clusters to which the modulated transmission symbols are allocated; and transmitting the IFFT-processed transmission signal.
Owner:SAMSUNG ELECTRONICS CO LTD
Separating motion from cardiac signals using second order derivative of the photo-plethysmogram and fast fourier transforms
The present invention is directed toward a pulse oximetry system for the determination of a physiological parameter capable of removing motion artifacts from physiological signals comprises a hardware subsystem and a software subsystem. The software subsystem is used in conjunction with the hardware subsystem to perform a method for removing a plurality of motion artifacts from the photo-plethysmographic data and for obtaining a measure of at least one physiological parameter from the data. The method comprises acquiring the raw photo-plethysmographic data, transforming the data into the frequency domain, analyzing the transformed data to locate a series of candidate cardiac spectral peaks (primary plus harmonics), reconstructing a photo-plethysmographic signal in the time domain with only the candidate cardiac spectral peaks (primary plus harmonics), computing the second order derivative of the reconstructed photo-plethysmographic signal, analyzing the candidate second order derivative photo-plethysmographic signal to determine the absence or presence of cardiac physiologic signal characteristics, and finally selecting the best physiologic candidate from the series of potential cardiac spectral peaks (primary plus harmonics) based upon a second derivative scoring system. This scoring system is preferentially based upon second derivative processing analysis, but can be equally applied using the first, third, fourth or other similar derivative processing analysis.
Owner:SPACELABS HEALTHCARE LLC
Frequency hopping spread spectrum system with high sensitivity tracking and synchronization for frequency unstable signals
InactiveUS6934316B2Improve dynamic rangeReduce sensitivityData switching by path configurationSynchronisation signal speed/phase controlFrequency-hopping spread spectrumFast Fourier transform
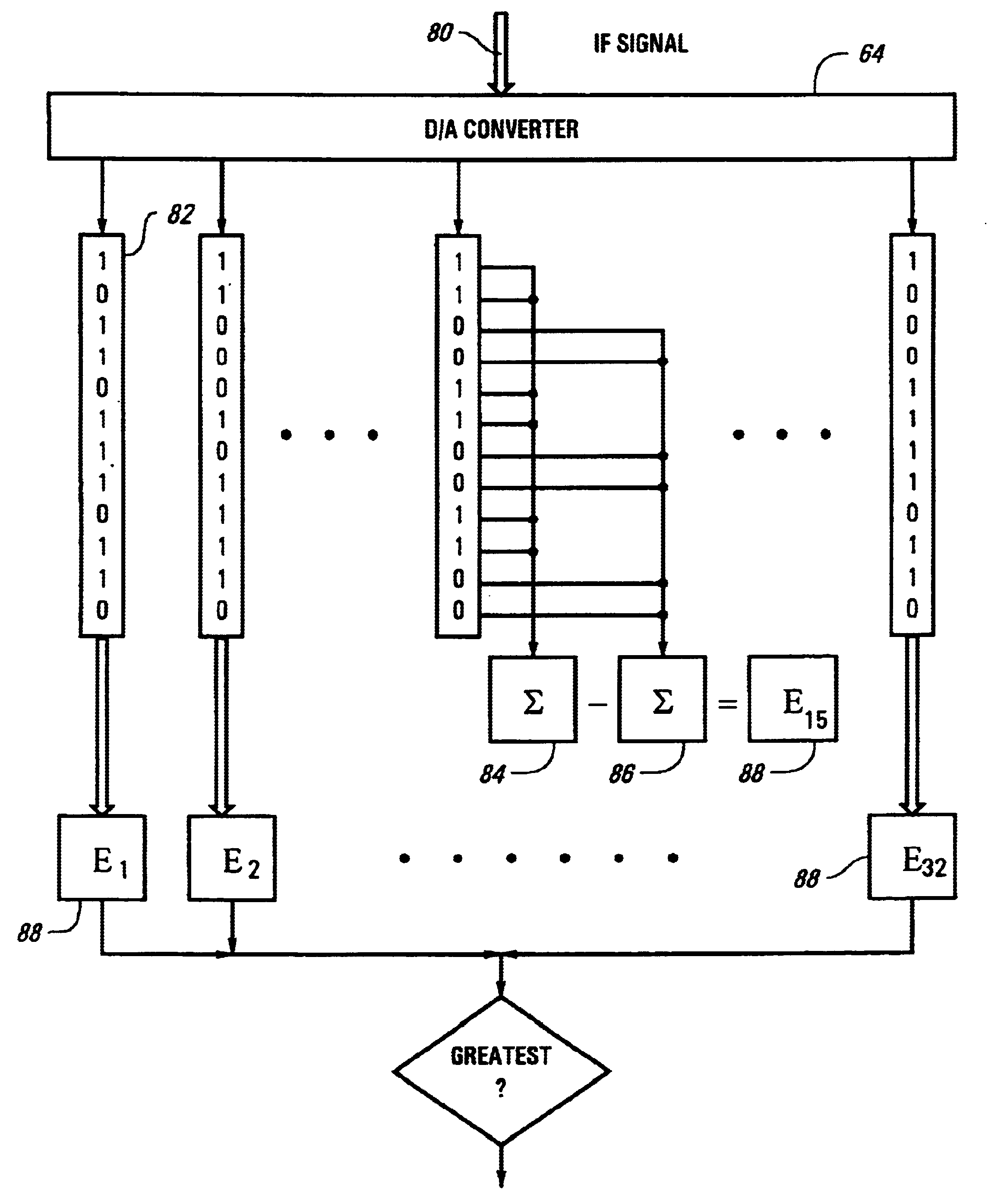
A wireless spread spectrum communication system for transmitting data includes a plurality of end point transmitters and at least one receiver. The end point transmitters transmit data via a frequency hopped spread spectrum signal where the transmitting signal is sent without the benefit of frequency stabilization. The receiver is responsive to the frequency hopping spread spectrum signals and includes a correlator and a signal processor. The correlator samples at least a first portion of a preamble of the signal and correlates the portion of the preamble with a known preamble pattern to determine a probability of correlation. The signal processor applies a Fast Fourier Transform algorithm to the signal in response to the probability of correlation to track a narrowband frequency of the signal based on at least a second portion of the preamble and to decode data encoded within the signal subsequent to the preamble.
Owner:ITRON
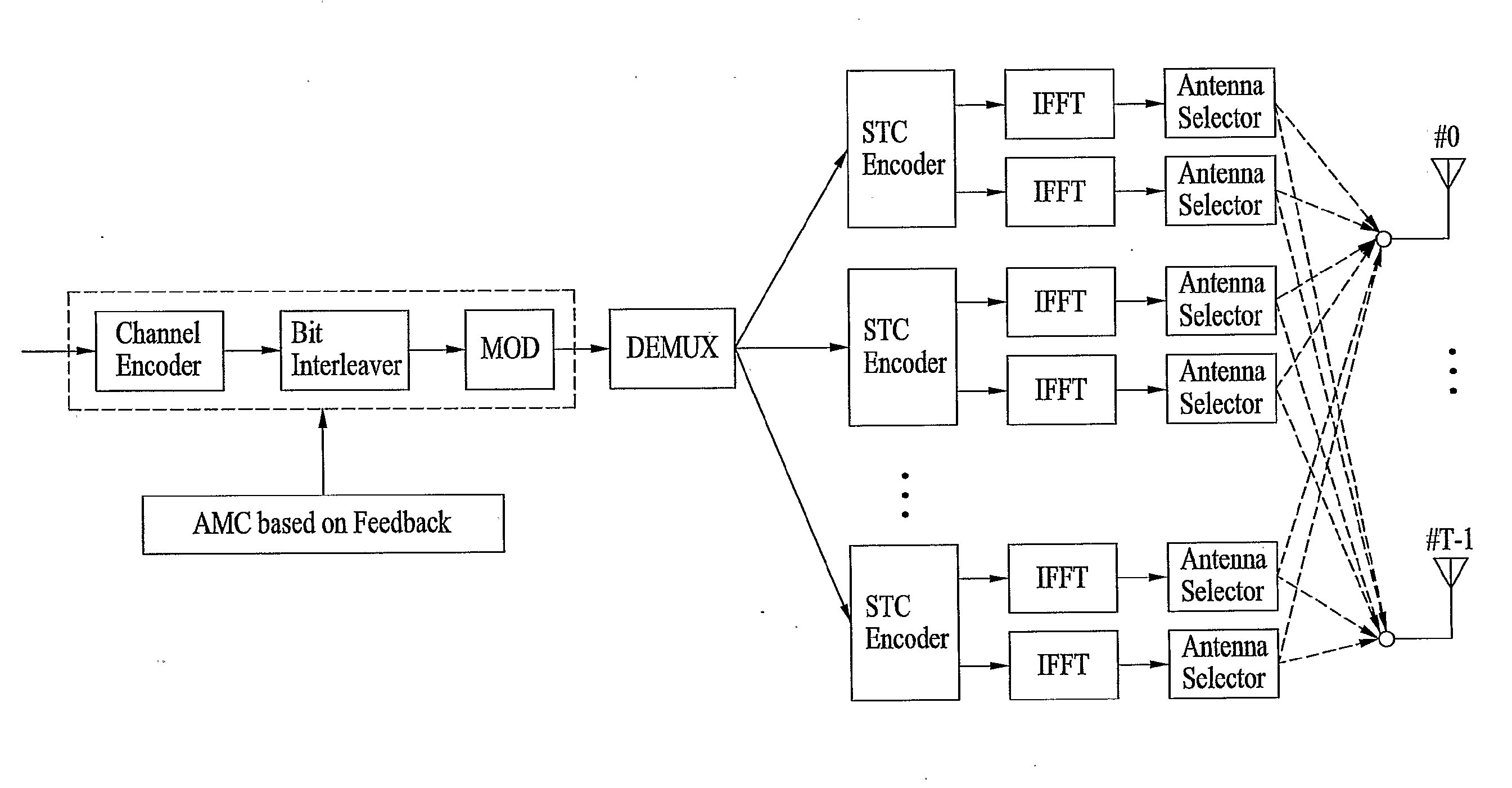
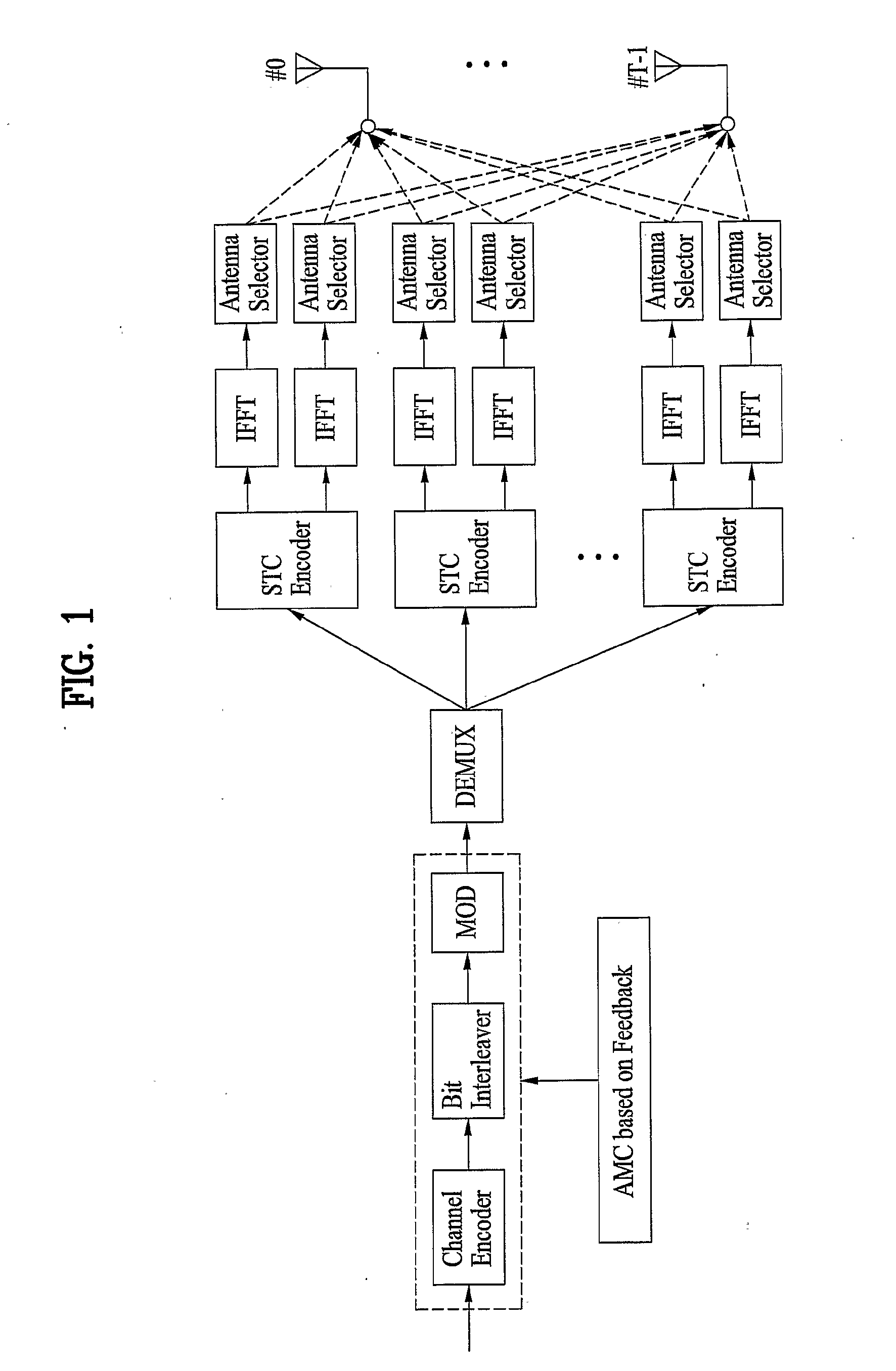
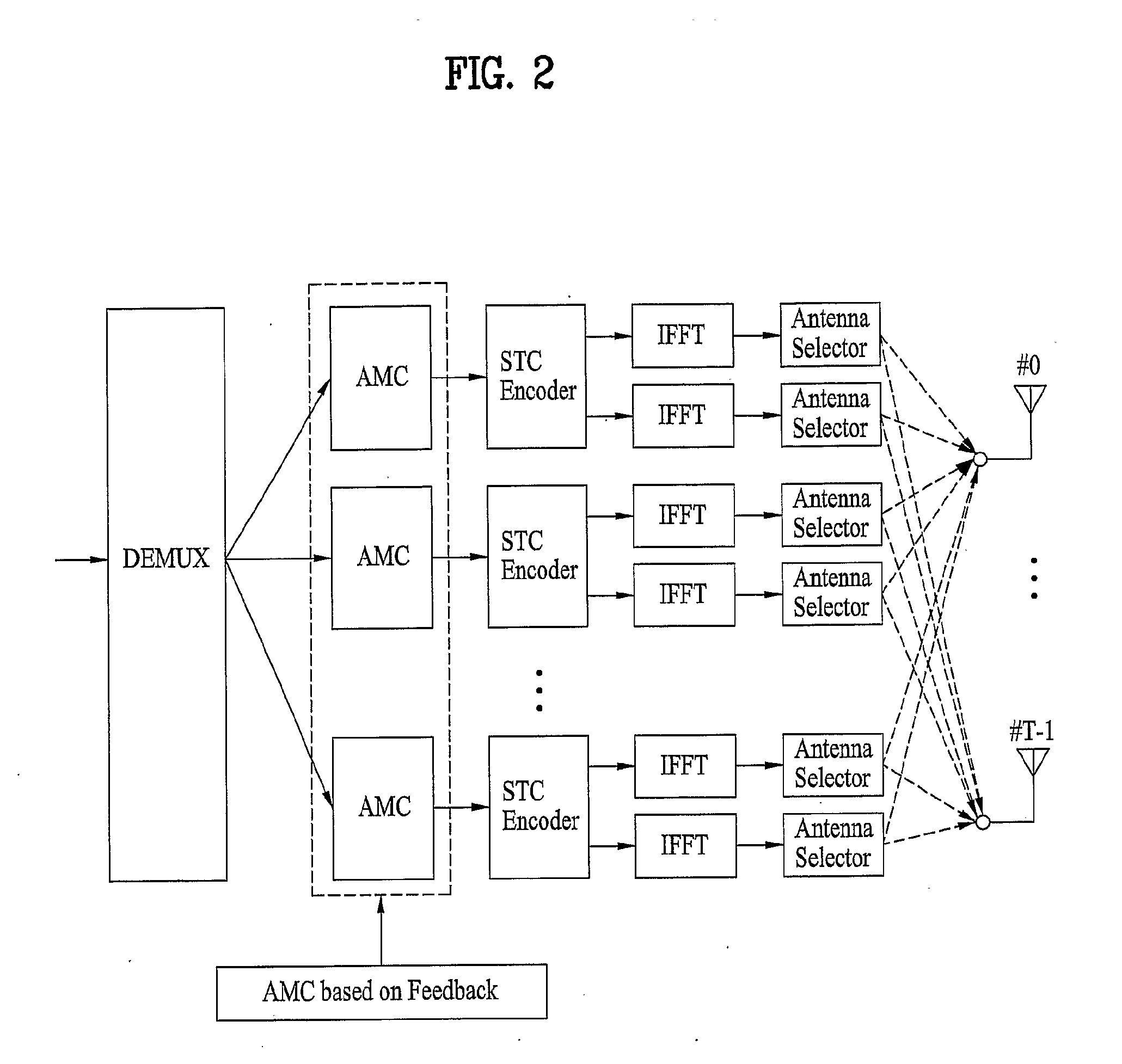
Method and apparatus for achieving transmit diversity and spatial multiplexing using antenna selection based on feedback information
InactiveUS20090316807A1Eliminate the problemSecret communicationRadio transmissionFast Fourier transformData stream
A method of achieving transmit diversity in a wireless communication system is disclosed. The method comprises encoding and modulating data stream based on feedback information, demultiplexing symbols to at least one encoder block, encoding the demultiplexed symbols by the at least one encoder block, transforming the encoded symbols by at least one inverse fast Fourier transform (IFFT) block, and selecting antennas for transmitting the symbols based on the feedback information.
Owner:LG ELECTRONICS INC
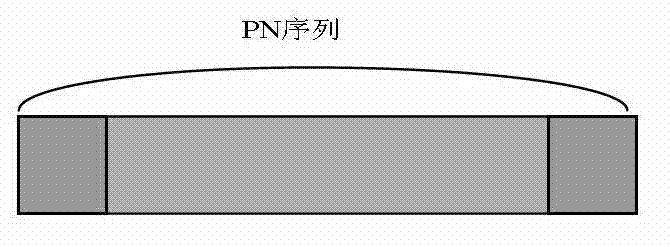
Synchronous processing method based on CMMB signals
InactiveCN102882670AHigh synchronization accuracyGood synchronizationBaseband system detailsMulti-frequency code systemsFast Fourier transformTime delays
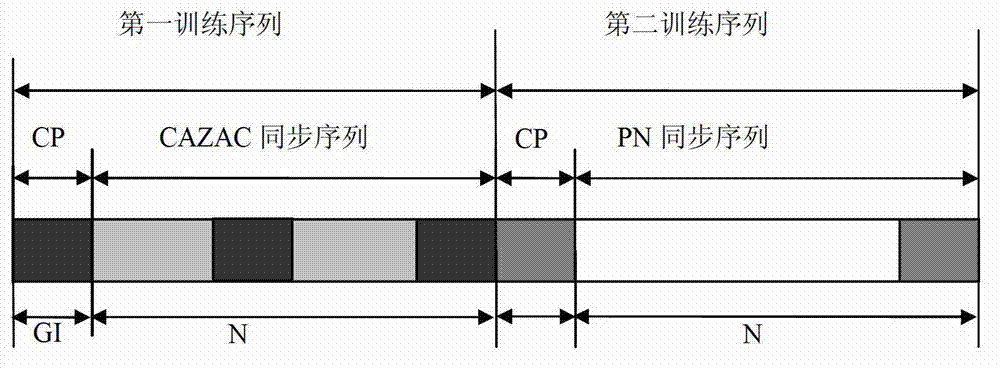
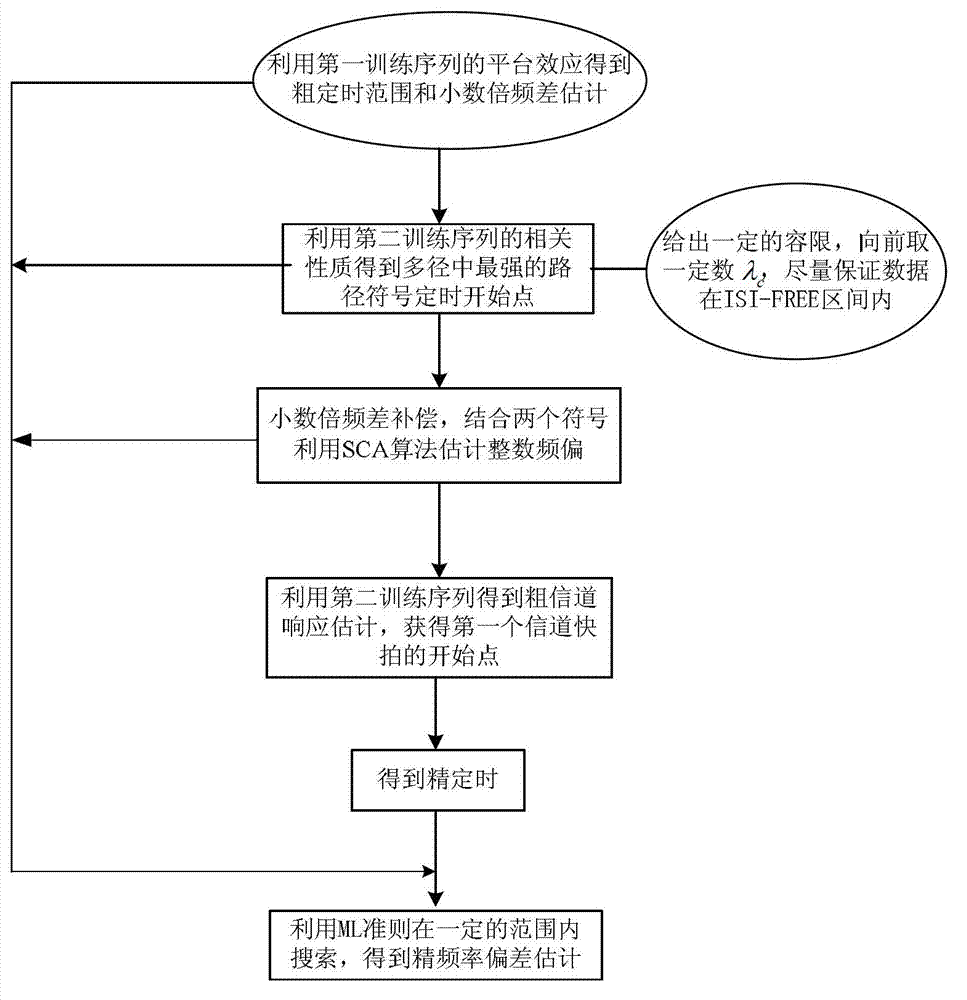
The invention provides a synchronous processing method based on new CMMB (China Mobile Multimedia Broadcasting) synchronous signals. The CMMB synchronous signals comprise first training sequences and second training sequences; the first training sequences comprise CAZAC (Constant Amplitude Zero Auto Correlation) sequences, and the second training sequences comprise PN (Pseudo-Noise) sequences; in the synchronous processing method, the CAZAC sequences are utilized to achieve coarse symbol timing offset estimation and decimal frequency offset coarse estimation; the PN sequences are utilized to achieve the estimation of strongest path time delay in multipath, and the multipath is taken as coarse symbol timing positioning; the CAZAC sequences and the PN sequences are utilized to achieve the integer frequency offset estimation; the fast Fourier transform (FFT) is performed on the PN sequences to achieve the channel response estimation so as to estimate a first path time delay and achieve the fine symbol timing position estimation; and a maximum likelihood (ML) criterion is utilized to process the PN sequences in the second training sequences to obtain the decimal frequency offset fine estimation. The synchronous processing method can effectively improve the synchronous accuracy and can achieve better synchronization performance in the mobile communication environment with low signal-to-noise ratio.
Owner:UNIV OF ELECTRONICS SCI & TECH OF CHINA
Apparatus and method for transmitting/receiving pilot signals in an OFDM communication system
InactiveUS20050099939A1Minimize overheadMulti-frequency code systemsOrthogonal multiplexFast Fourier transformCommunications system
A radio communication system divides an entire frequency band into a plurality of subcarrier bands, forms a symbol from signals on the subcarrier bands, forms a frame from a plurality of symbols, transmits a pilot signal within symbols in a predetermined position of the frame, and transmits a data signal within symbols other than the symbols for transmitting the pilot signal. A transmitter generates the pilot signal, performs an inverse fast Fourier transform (IFFT) on the pilot signal by applying an IFFT size which is less than an IFFT size applied to the data signal, and transmits the IFFT-processed reference signal to a receiver.
Owner:SAMSUNG ELECTRONICS CO LTD
Apparatus and method for reducing an error vector magnitude in an orthogonal frequency division multiplexing receiver
InactiveUS20060159006A1Degradation in error vector magnitudeSimple structureModulated-carrier systemsOrthogonal multiplexFast Fourier transformGuard interval
An apparatus and a method for reducing an error vector magnitude in an orthogonal frequency division multiplexing (OFDM) receiver. The method includes the steps of inputting a receiving symbol including a guard interval and an effective symbol interval following the guard interval, in which a front portion of the guard interval and a rear portion of the effective symbol interval have windowing intervals corresponding to windowing of a transmitter, and replacing a signal of the rear windowing interval with a signal of an interval between the front windowing interval and the effective symbol interval, thereby outputting a signal of the effective symbol interval, which substitutes for a signal of the rear windowing interval, to a fast Fourier transform (FFT) section.
Owner:SAMSUNG ELECTRONICS CO LTD
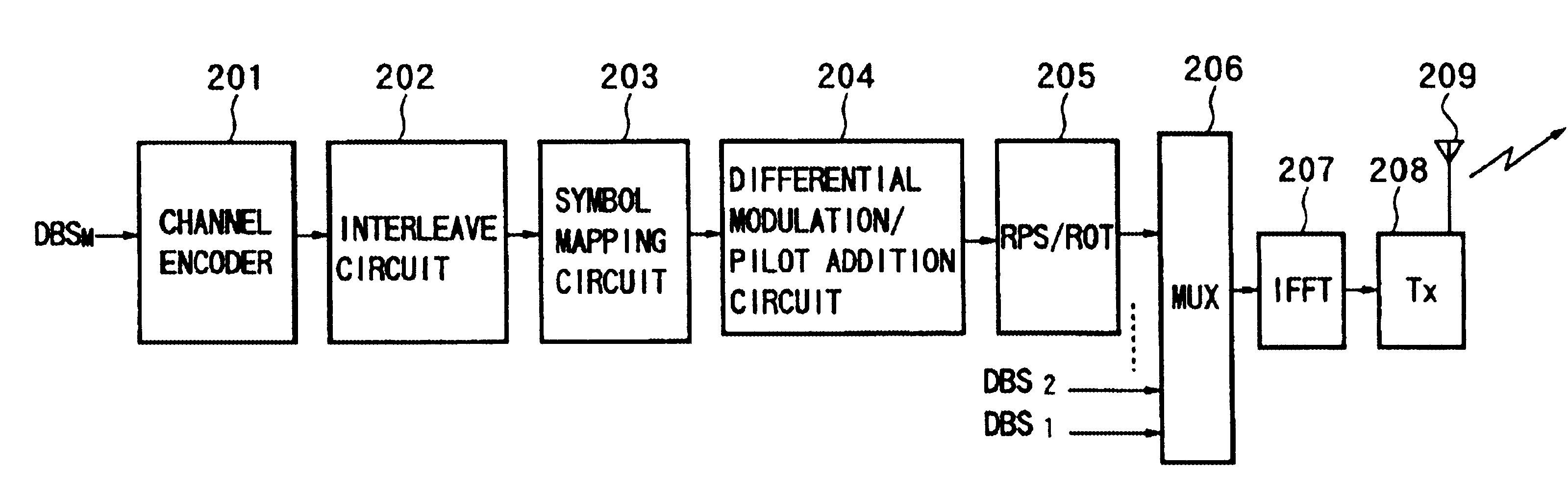
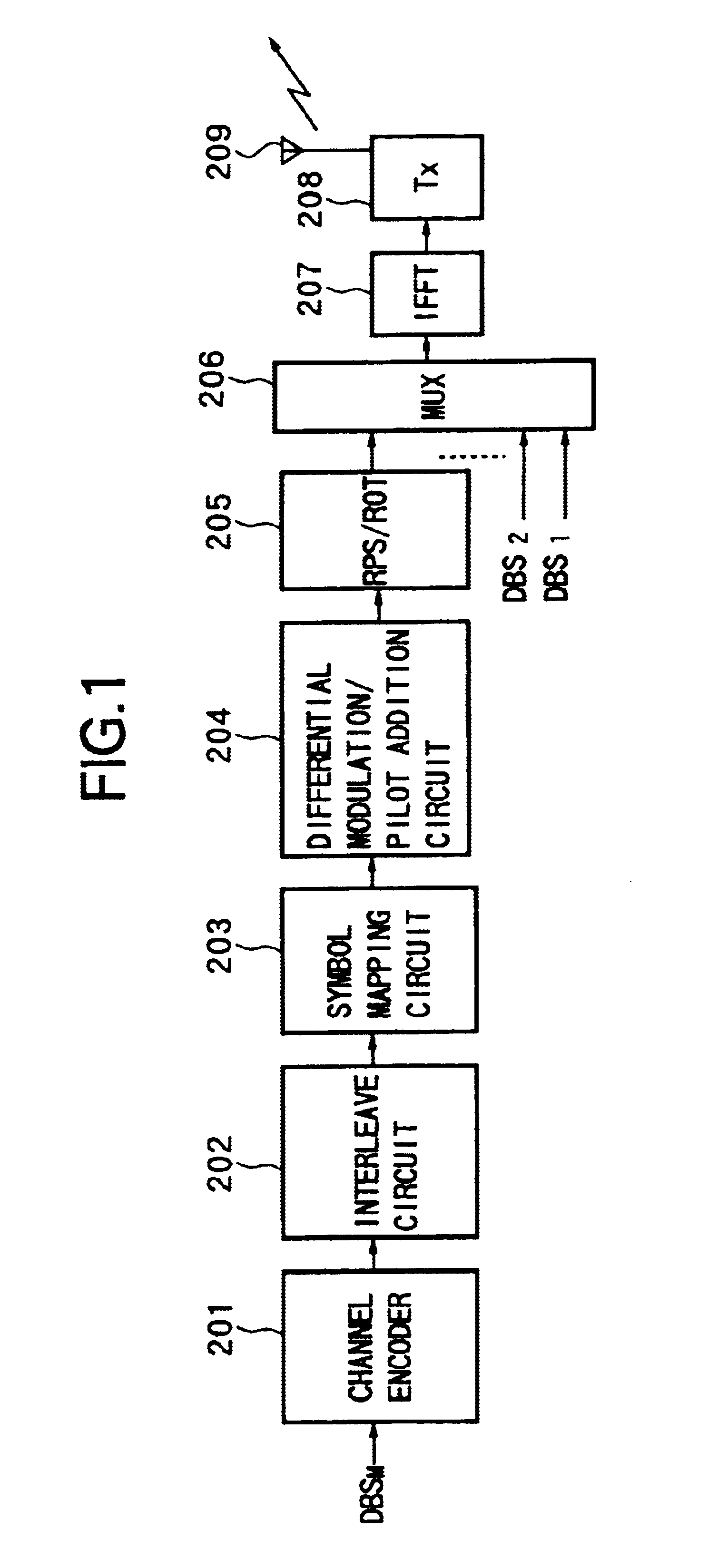
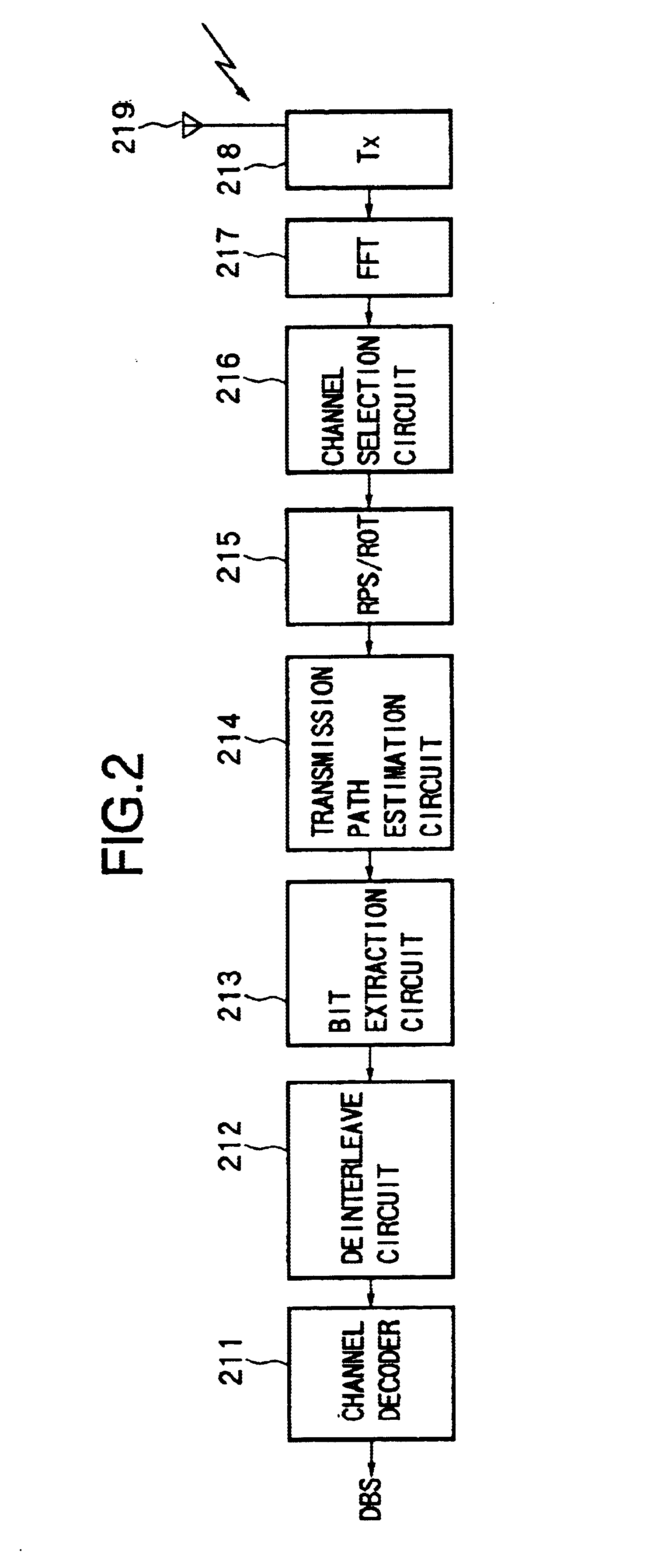
Transmitting apparatus, receiving apparatus, communication system, transmission method, reception method, and communication method
InactiveUS6888789B1Improve efficiencyReduce rateTransmission control/equlisationMultiple modulation transmitter/receiver arrangementsFast Fourier transformCommunications system
A transmitting apparatus, receiving apparatus, communication system, and a signal processing method of each applying a suitable modulation method and transmission path estimation method in accordance with characteristics of the transmission information for improving the transmission efficiency operate so that at the transmission side, the ratio of adding transmission path estimation pilot symbols is suitably controlled in accordance with an aspect of the dat transmitted, for example, the size of the packets transmitted and the state of the transmission path, wherein the transmission data is mapped by the selected modulation method, and the signal is processed in accordance with the method of estimation of the transmission path, and the transmission signal is produced by inverse fast Fourier transform processing and transmitted. At the reception side, the received signal is fast Fourier transformed, the transmission path is estimated by the transmission path estimation method selected at the transmission side, the received signal is correct in accordance with result, and the received data is reproduced in accordance with the modulation method. Therefore, it is possible to always adopt the optimum transmission method in accordance with the attribute of the transmission data etc. and possible to realize an improvement of a transmission efficiency and an enhancement of the quality of communication.
Owner:REDWOOD TECHNOLOGIES LLC
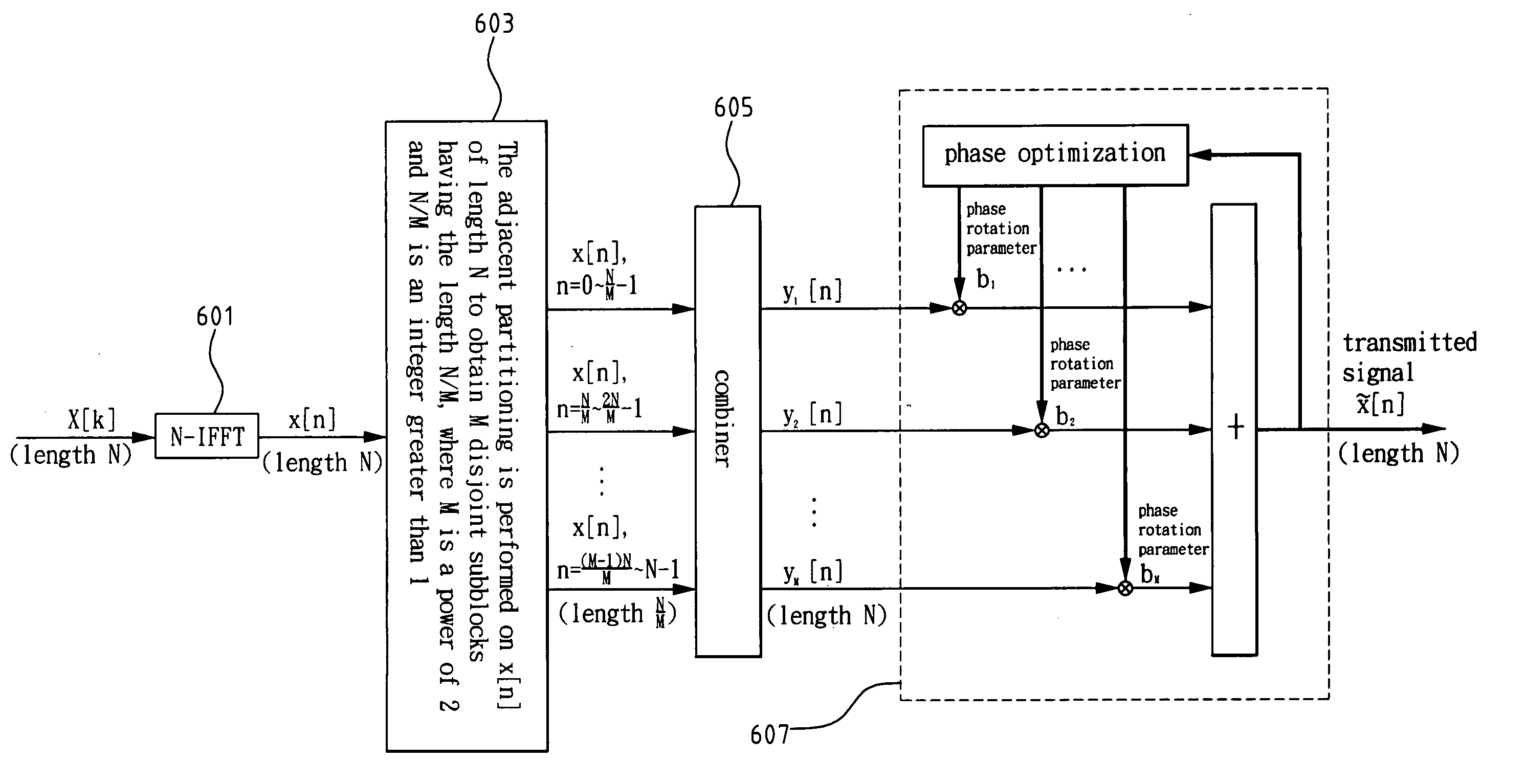
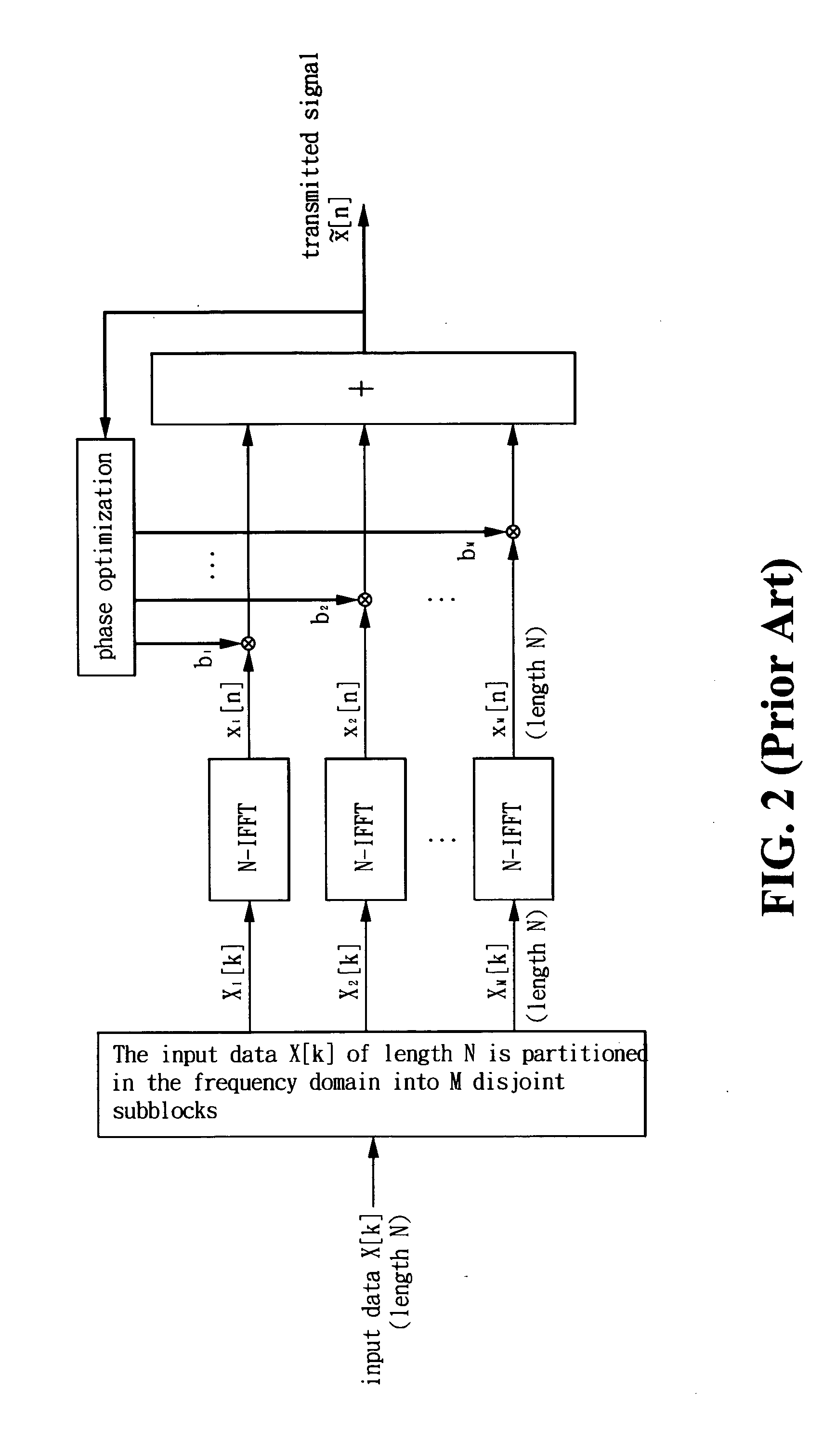
Method and apparatus for PAPR reduction of an OFDM signal
InactiveUS20050270968A1Shorten the lengthReduce the amount of calculationSecret communicationMulti-frequency code systemsTime domainFast Fourier transform
An apparatus and a method for peak-to-average power ratio reduction of an OFDM signal are disclosed. The method uses the interleaved characteristics of partial transmit sequences to partition input data x[n] of length N into several disjoint subblocks in time domain, and a complete N-point signal {tilde over (x)}[n] is composed after phase optimization, where N is the length of an OFDM signal and n=0, 1, . . . , N−1. Accordingly, the apparatus comprises an N-point inverse fast Fourier transform (N-IFFT), a de-multiplexer, a combiner, a set of memory and an adder. This invention uses only one N-IFFT, whereby it can achieve significant computation reduction. This invention requires (N / 2)log2 N complex multiplications and N memory units. It also preserves the inherent property as well as advantages of an OFDM system.
Owner:IND TECH RES INST
Digital Video Broadcast Service Discovery
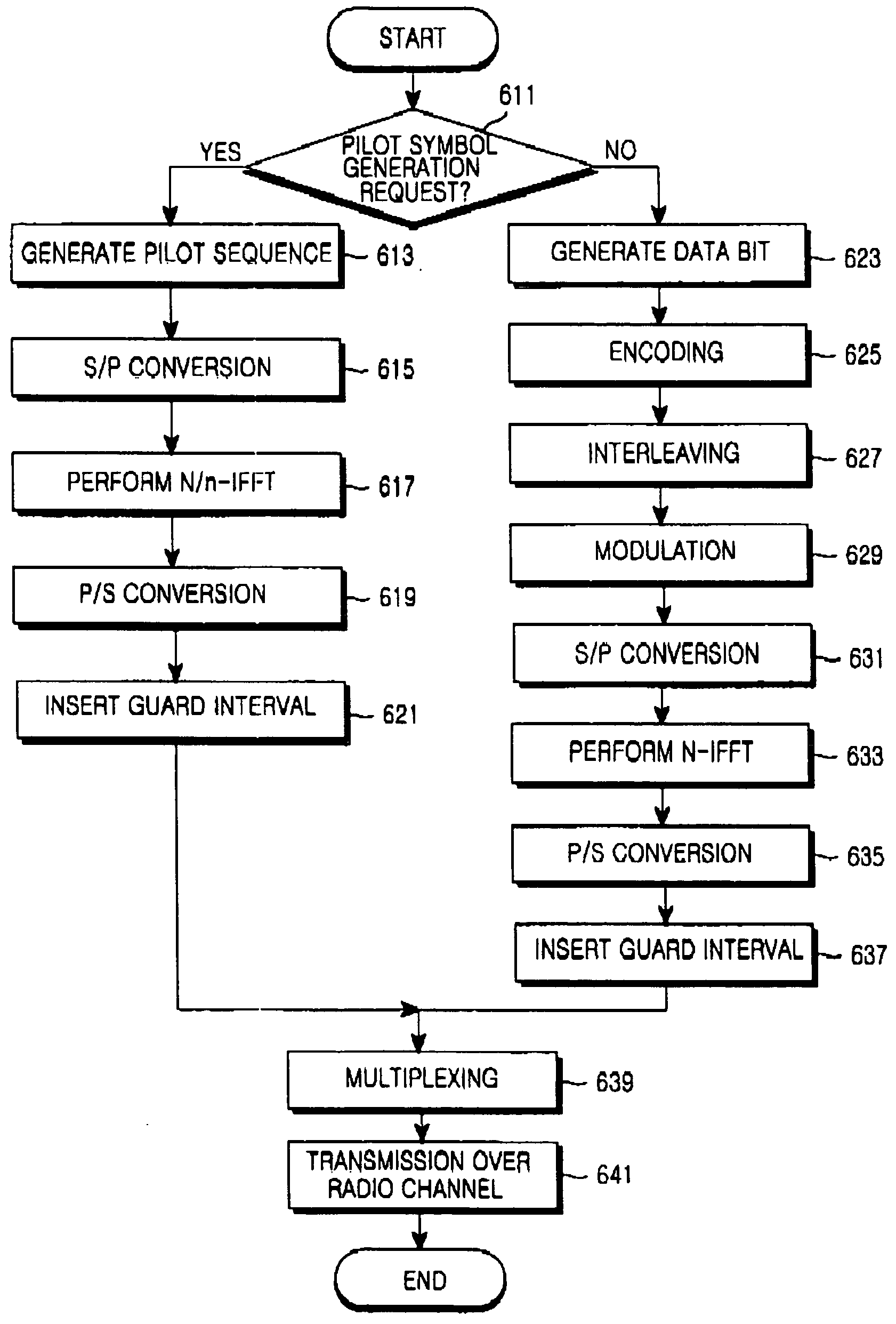
Embodiments are directed to binary phase shift key modulating a first pilot symbol according to a reference sequence, and differentially binary phase shift key modulating a second pilot symbols. The original reference sequence and the delayed differentially modulated sequence are then combined before performing an Inverse Fast Fourier Transform and inserting a guard interval. Receiver operations are an inverse of the transmitter operations, which were just discussed. The receiver does not have to know the reference sequence. Embodiments are directed to specifying a plurality of seeds that are bit patterns each having r bits not all of which have a value of zero, extending the seeds into respective sequences by applying to each seed a recurrence formula; and using one of the sequences as a comb sequence and using the sequences other than the comb sequence as binary phase shift keying patterns.
Owner:SAMSUNG ELECTRONICS CO LTD
Highly bandwidth-efficient communications
InactiveUS7106781B2Efficient processingEnhance signal to noise and interference ratio of signalSpatial transmit diversityModulated-carrier systemsFrequency spectrumCarrier signal
Owner:AT&T WIRELESS SERVICES
Cooperative Communication and Shared Handoff among Base, Relay, and Mobile Stations in OFDMA Cellular Networks
InactiveUS20080165866A1Multiplex communicationRadio/inductive link selection arrangementsFast Fourier transformSpatial mapping
In a cellular network, symbols are encoded and modulated to produce a modulated signal The modulated signal is mapped to a subcarrier using a spatial mapping matrix. An inverse fast Fourier transform is applied to the mapped signal to produce groups of tones. The groups of tones are transmitting concurrently to multiple receivers using the same channel as orthogonal frequency-division multiplexing access (OFDMA) signals. There is one group of tones for each receiver.
Owner:MITSUBISHI ELECTRIC RES LAB INC
Radar-imaging of a scene in the far-field of a one-or two-dimensional radar array
InactiveUS20110140954A1Efficient implementationImprove visualizationRadio wave reradiation/reflectionFast Fourier transformRadar imaging
A method of radar-imaging a scene in the far-field of a one-dimensional radar array, comprises providing an array of backscatter data D(fm, x′n) of the scene, these backscatter data being associated to a plurality of positions x′n, n=0 . . . N−1, N>1, that are regularly spaced along an axis of the radar array. The backscatter data for each radar array position x′n are sampled in frequency domain, at different frequencies fm, m=0 . . . M−1, M>1, defined by fm=fc−B / 2+m−Δf, where fc represents the center frequency, B the bandwidth and Δf the frequency step of the sampling. A radar reflectivity image 1(αm′, βn′) is computed in a pseudo-polar coordinate system based upon the formula (2) with formula (3) where j represents the imaginary unit, formula (A) is the baseband frequency, FFT2D denotes the 2D Fast Fourier Transform operator, αm′, m′=0 . . . M−1, and βn′, n′=0 . . . N−1 represent a regular grid in the pseudo-polar coordinate system, and Pmax is chosen >0 depending on a predefined accuracy to be achieved. A corresponding method of radar-imaging a scene in the far-field of a two-dimensional radar array is also proposed.I(αm′,βn′)=∑p=0PmaxIp(αm′,βn′),Formula(2)I(αm′,βn′)=1p![-j2πβn′fc]pFFT2D[D(fm,xn′)(f^m,xn′)p],Formula(3)f^m=-B / 2+m·ΔfFormula(A)
Owner:THE EURO UNION
Method for Automatic Segmentation of Images
InactiveUS20100215238A1Simplify the segmentation processSimple processImage enhancementImage analysisContour segmentationPattern recognition
A method for automatic left ventricle segmentation of cine short-axis magnetic resonance (MR) images that does not require manually drawn initial contours, trained statistical shape models, or gray-level appearance models is provided. More specifically, the method employs a roundness metric to automatically locate the left ventricle. Epicardial contour segmentation is simplified by mapping the pixels from Cartesian to approximately polar coordinates. Furthermore, region growing is utilized by distributing seed points around the endocardial contour to find the LV myocardium and, thus, the epicardial contour. This is a robust technique for images where the epicardial edge has poor contrast. A fast Fourier transform (FFT) is utilized to smooth both the determined endocardial and epicardial contours. In addition to determining endocardial and epicardial contours, the method also determines the contours of papillary muscles and trabeculations.
Owner:SUNNYBROOK HEALTH SCI CENT
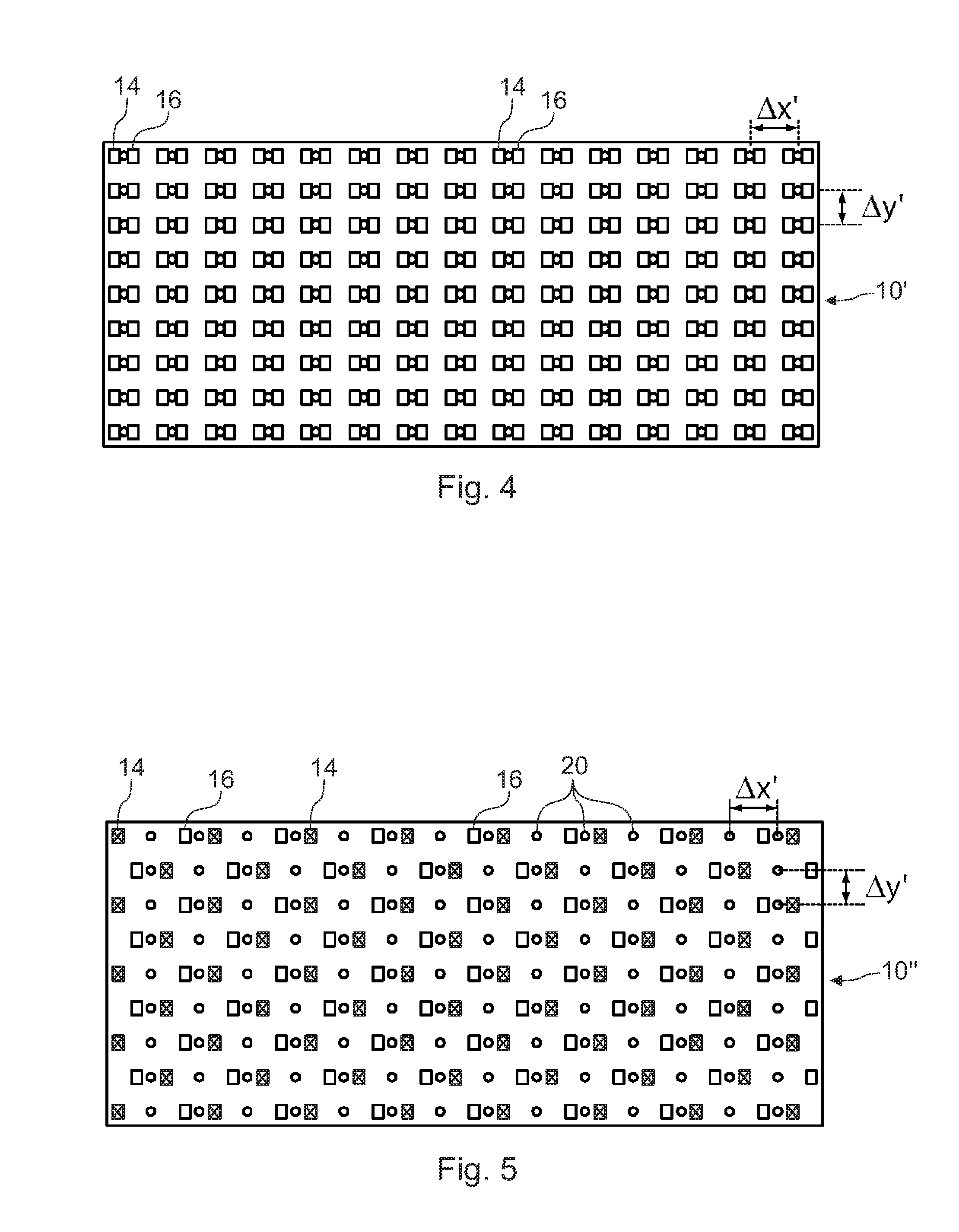
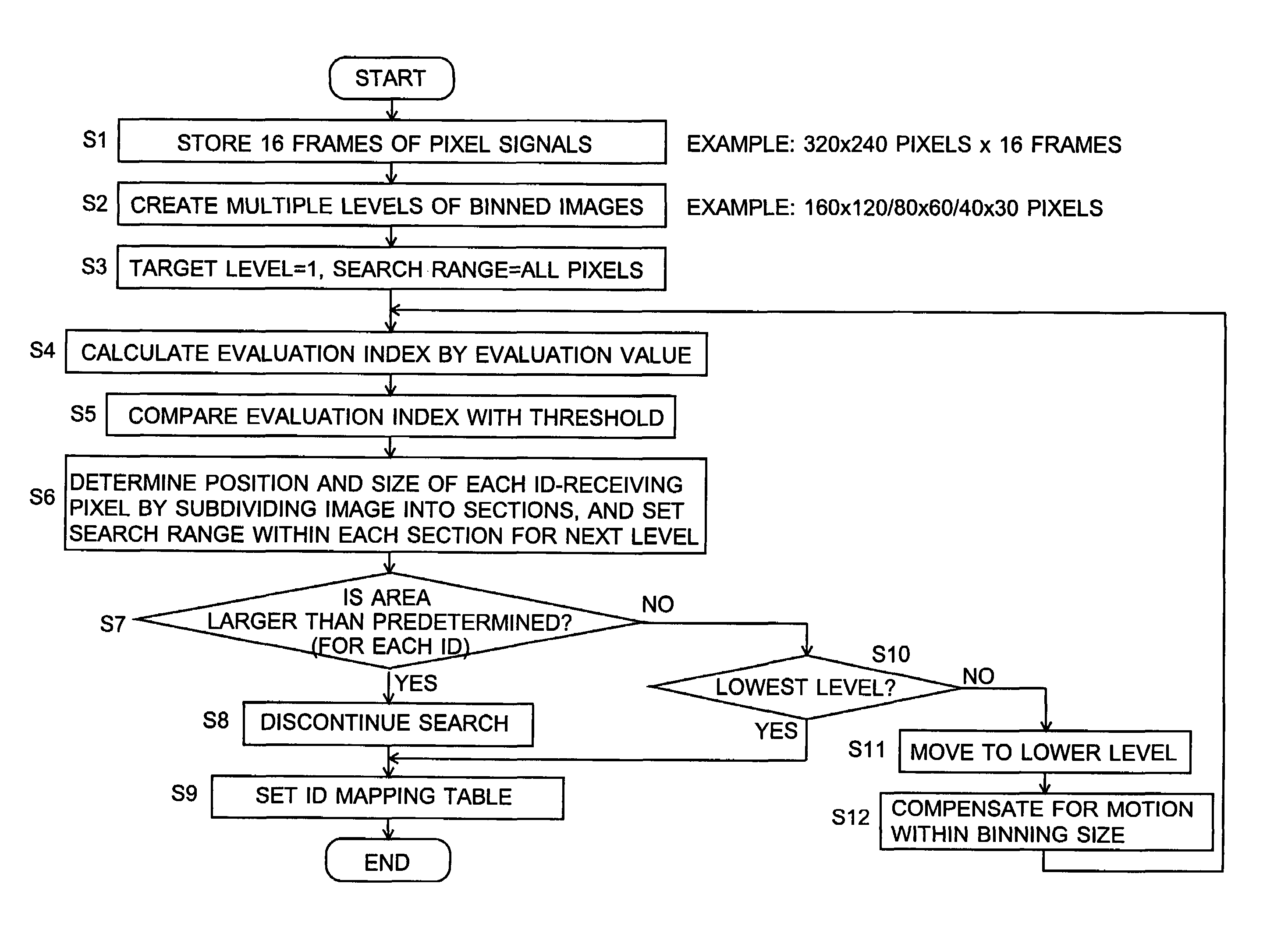
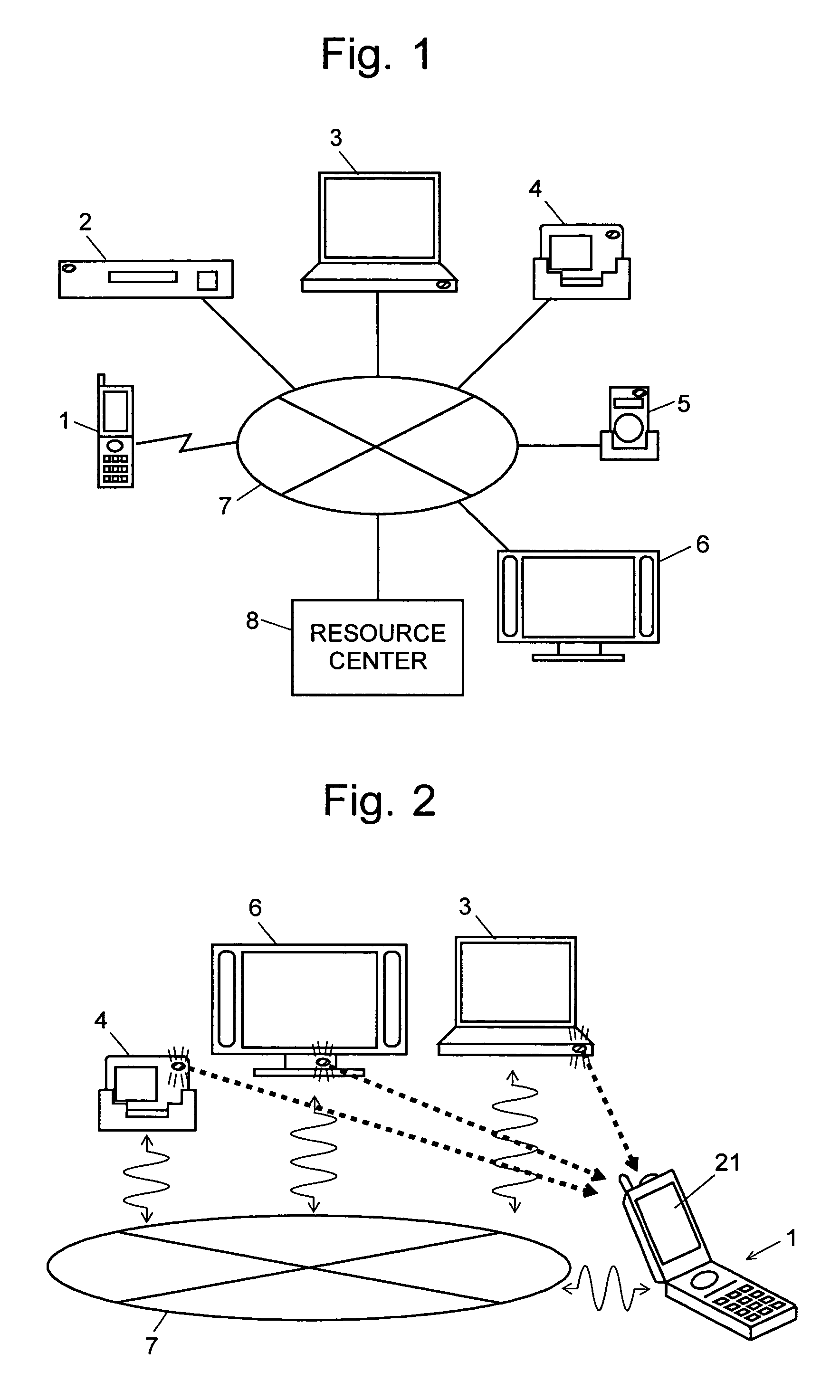
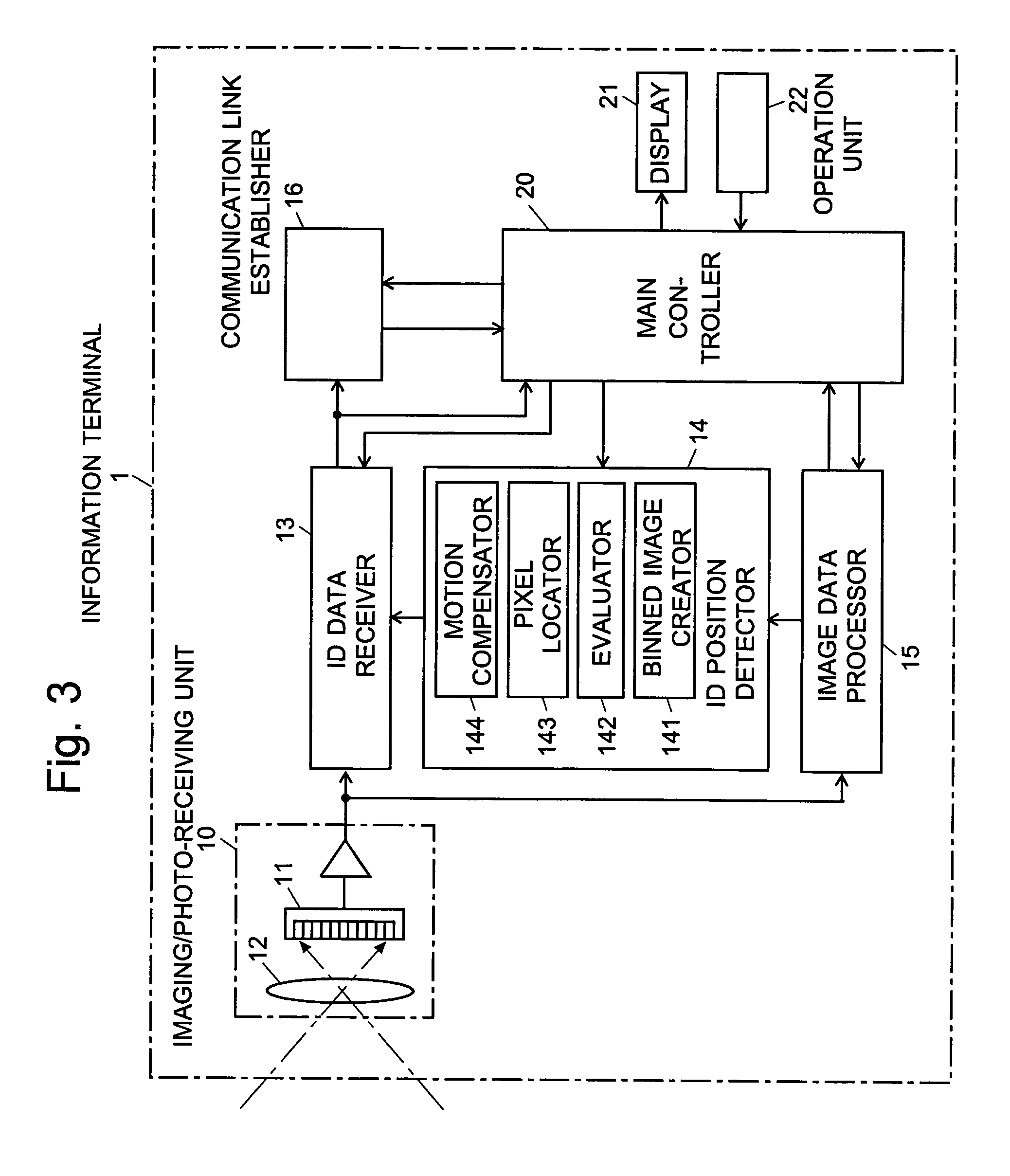
Information-processing device and information-processing system
InactiveUS7502053B2Reduce in quantityReduce the number of timesTelevision system detailsTelevision system scanning detailsInformation processingInformation device
For an information terminal to be operated by users for collecting predetermined pieces of information from remote information devices by free-space optical communication, the present invention provides a technique for suppressing the power consumption of the information terminal by minimizing the amount of calculation performed to collect the aforementioned information. According to the present invention, each information device emits ID light on which a low-frequency pilot signal is superimposed. The information terminal captures a series of frames of images including the ID light and locates the ID light within the images by the following steps: (1) creating multiple levels of binned images having different resolutions for each frame of the image; (2) calculating an evaluation index for each pixel within a target range of the binned images at each level, from the lowest to the highest resolution, where the target range is narrowed every time the process switches over to a lower level. In (2), the evaluation index is calculated by an evaluation function including fast Fourier transformation performed throughout the series of frames of images. The evaluation index thus calculated is compared with a threshold to determine whether the pixel concerned is receiving ID light. The present technique significantly reduces the number of pixel to be analyzed and evaluated, thereby decreasing the total number of arithmetic operations to be performed using the evaluation function. Thus, the power consumption is suppressed.
Owner:JAPAN SCI & TECH CORP +2
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com