Patents
Literature
Hiro is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
1621 results about "Automaton" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
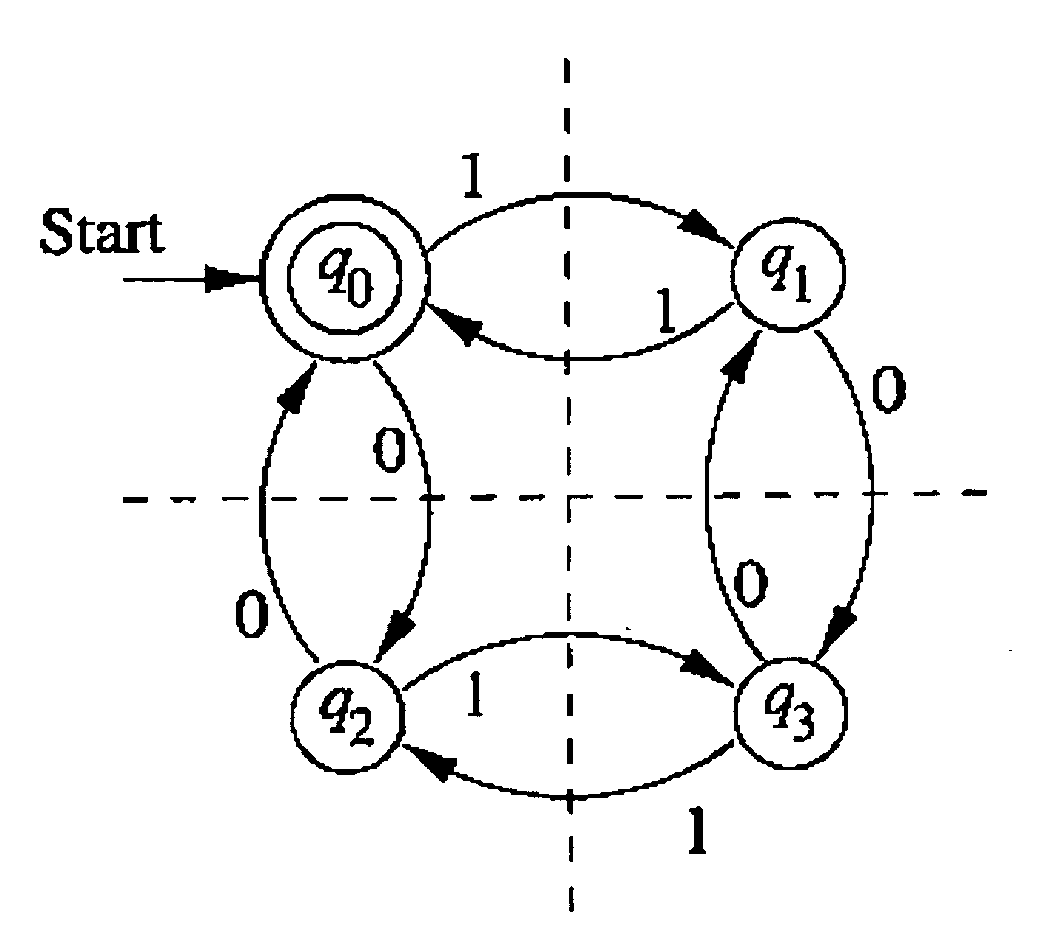
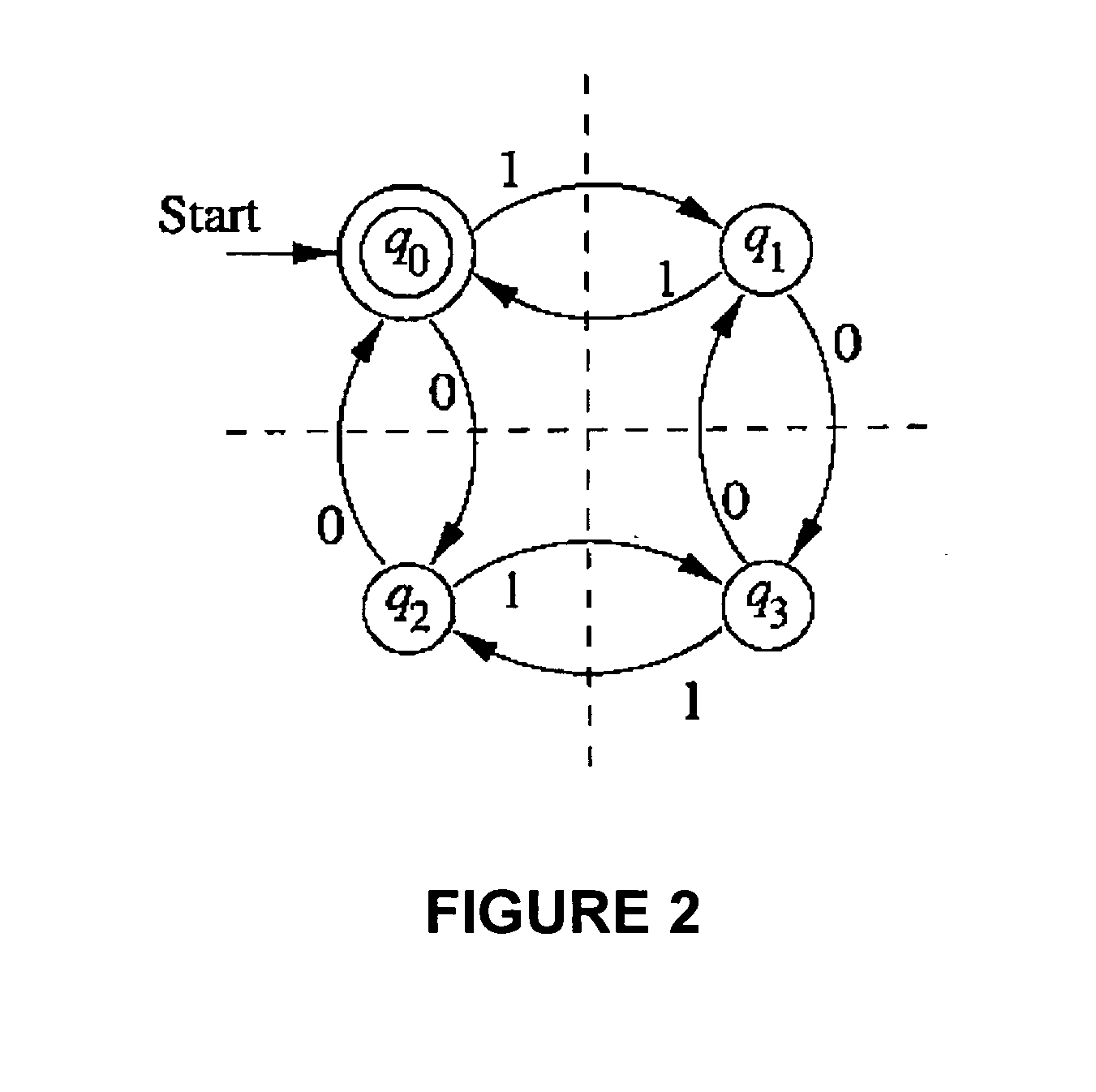
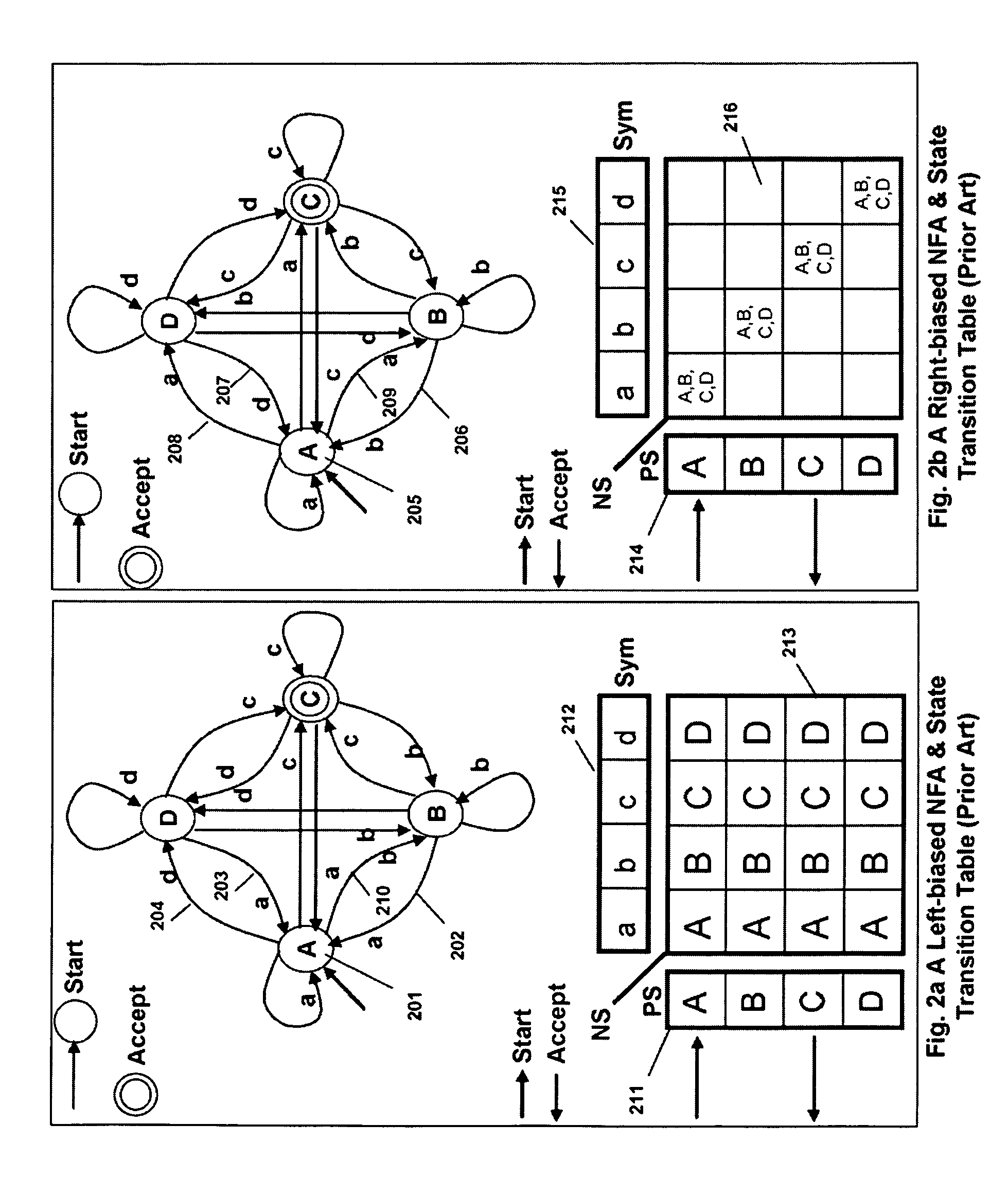
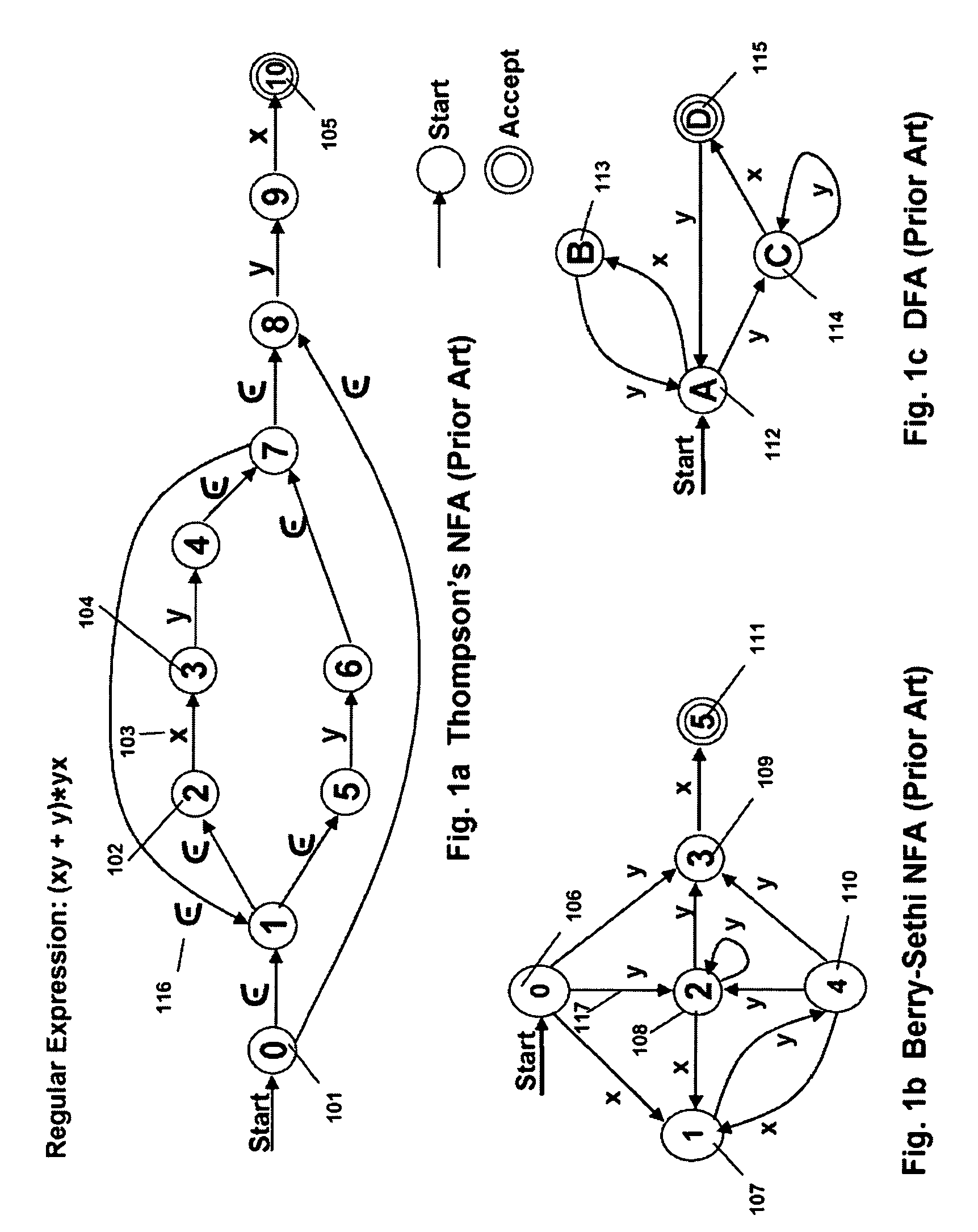
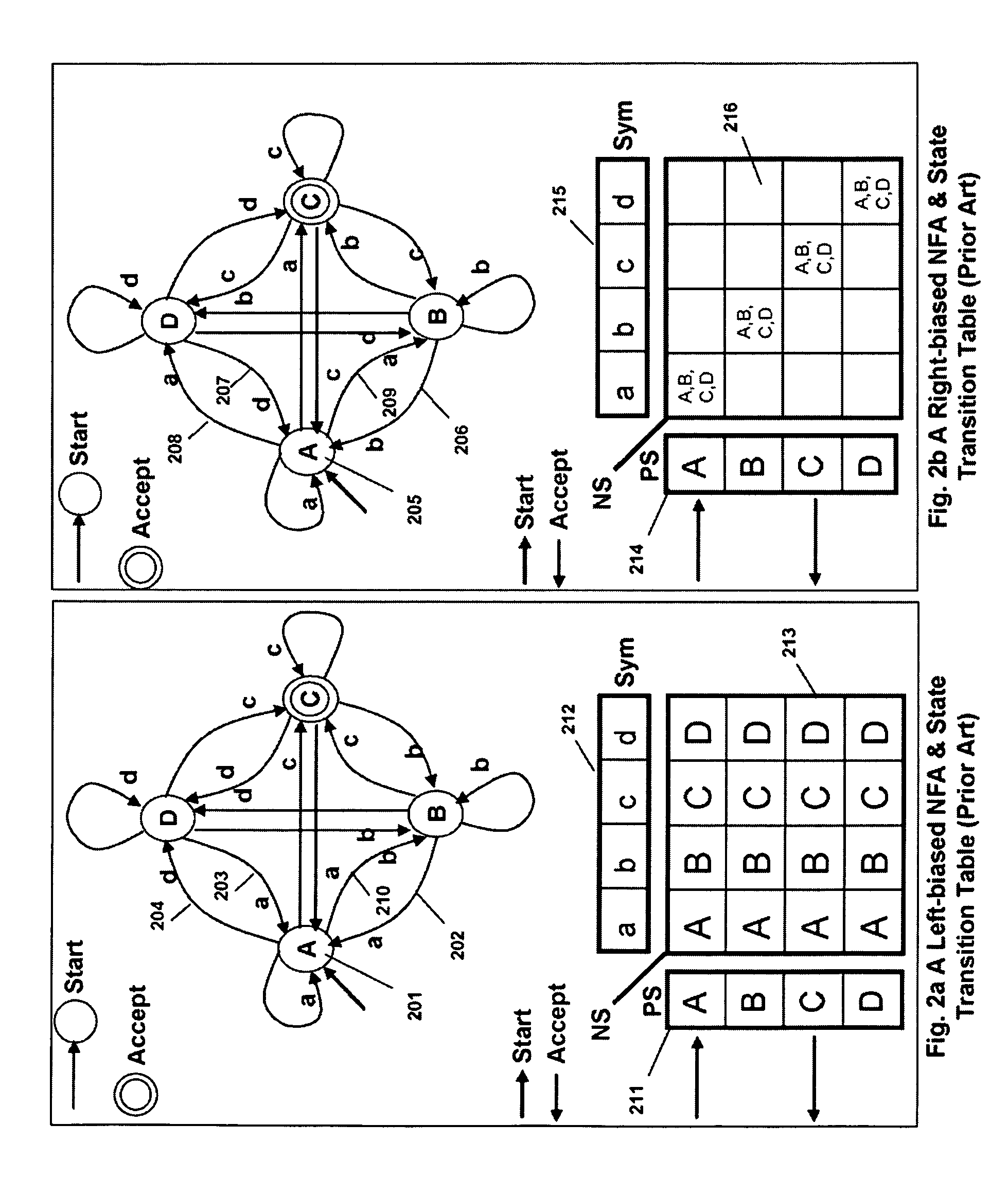
An automaton (/ɔːˈtɒmətən/; plural: automata or automatons) is a self-operating machine, or a machine or control mechanism designed to automatically follow a predetermined sequence of operations, or respond to predetermined instructions. Some automata, such as bellstrikers in mechanical clocks, are designed to give the illusion to the casual observer that they are operating under their own power.
Systems and methods for generating weighted finite-state automata representing grammars
InactiveUS7181386B2Natural language analysisDigital data processing detailsFinite state transducerAutomaton
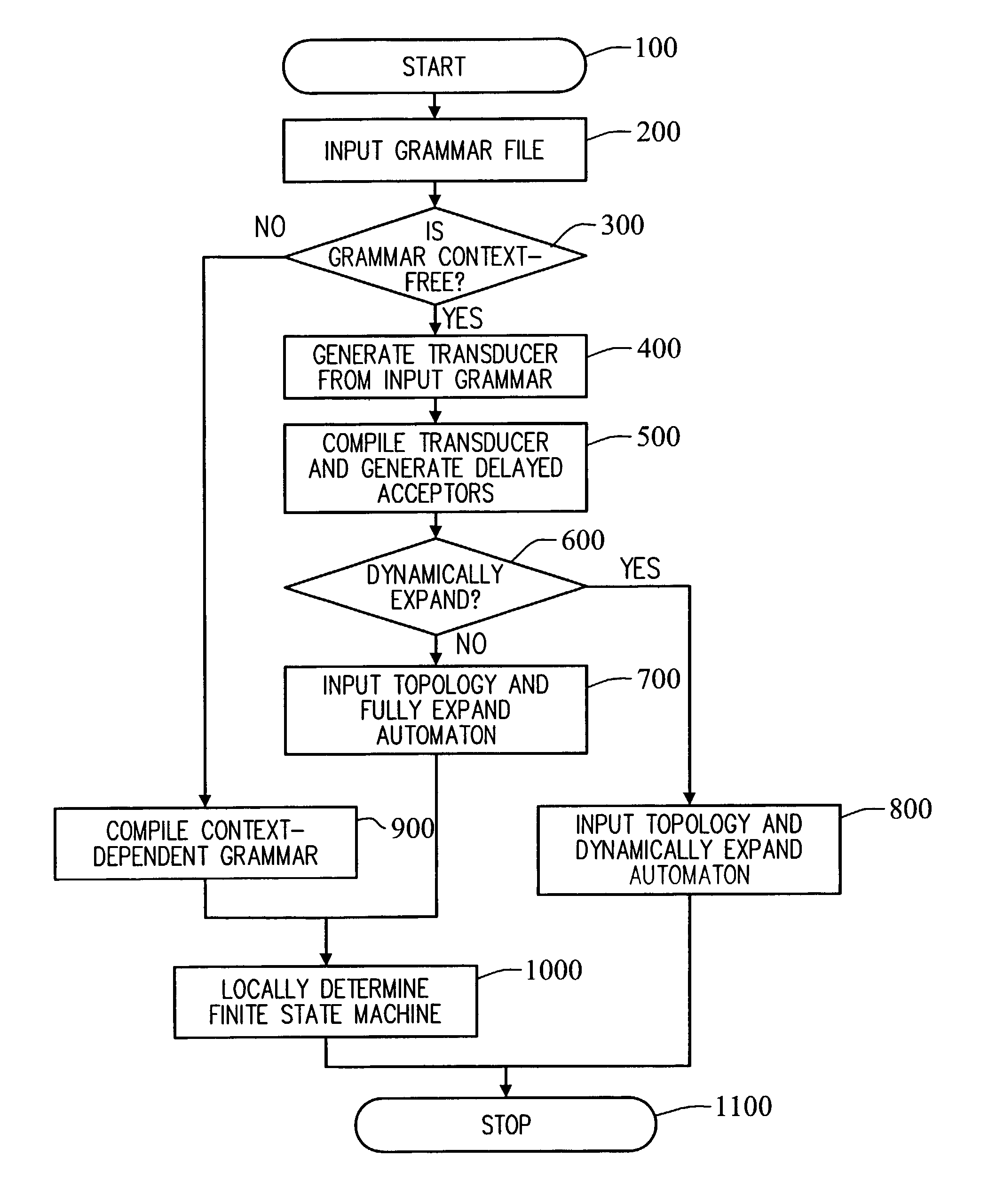
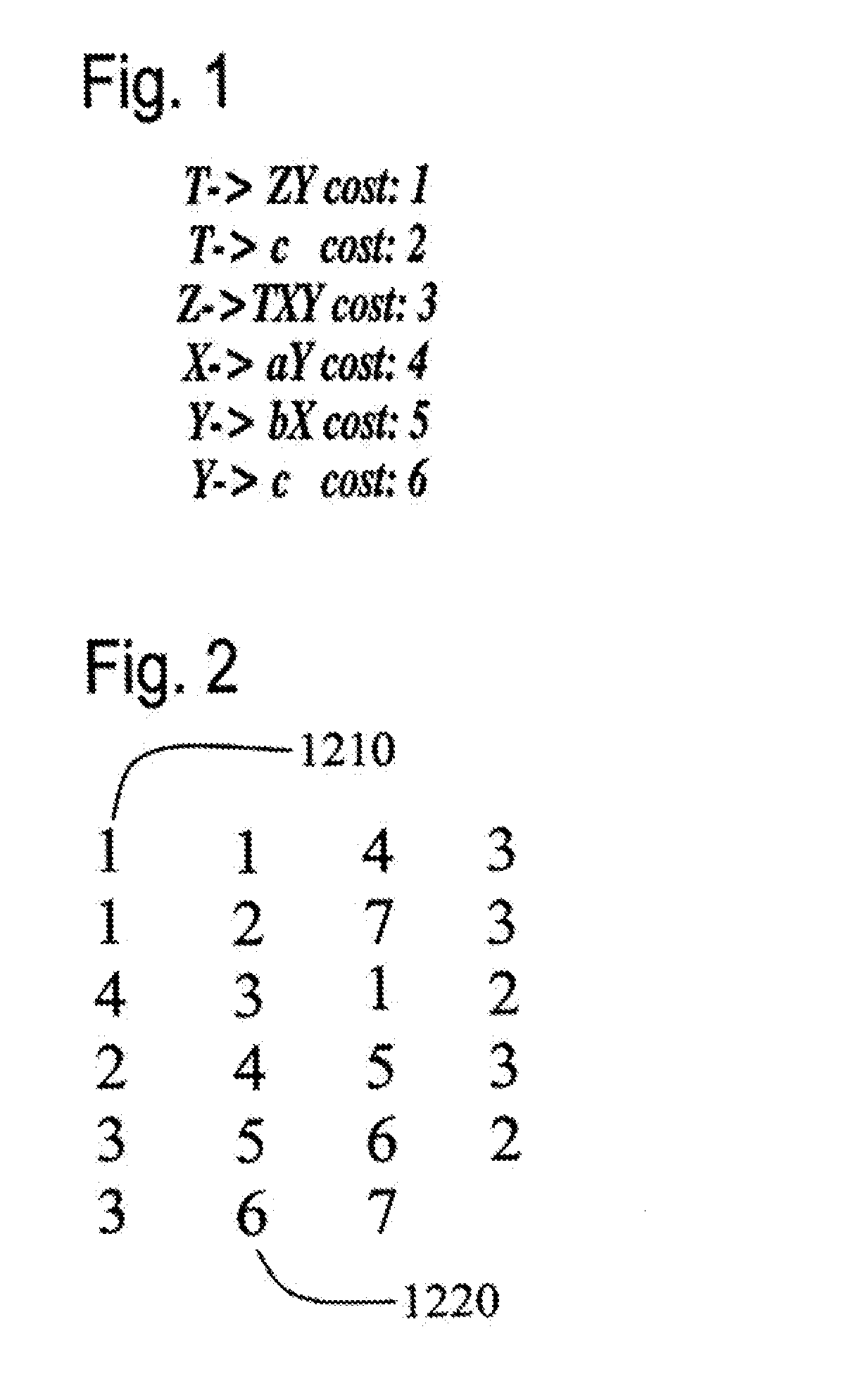
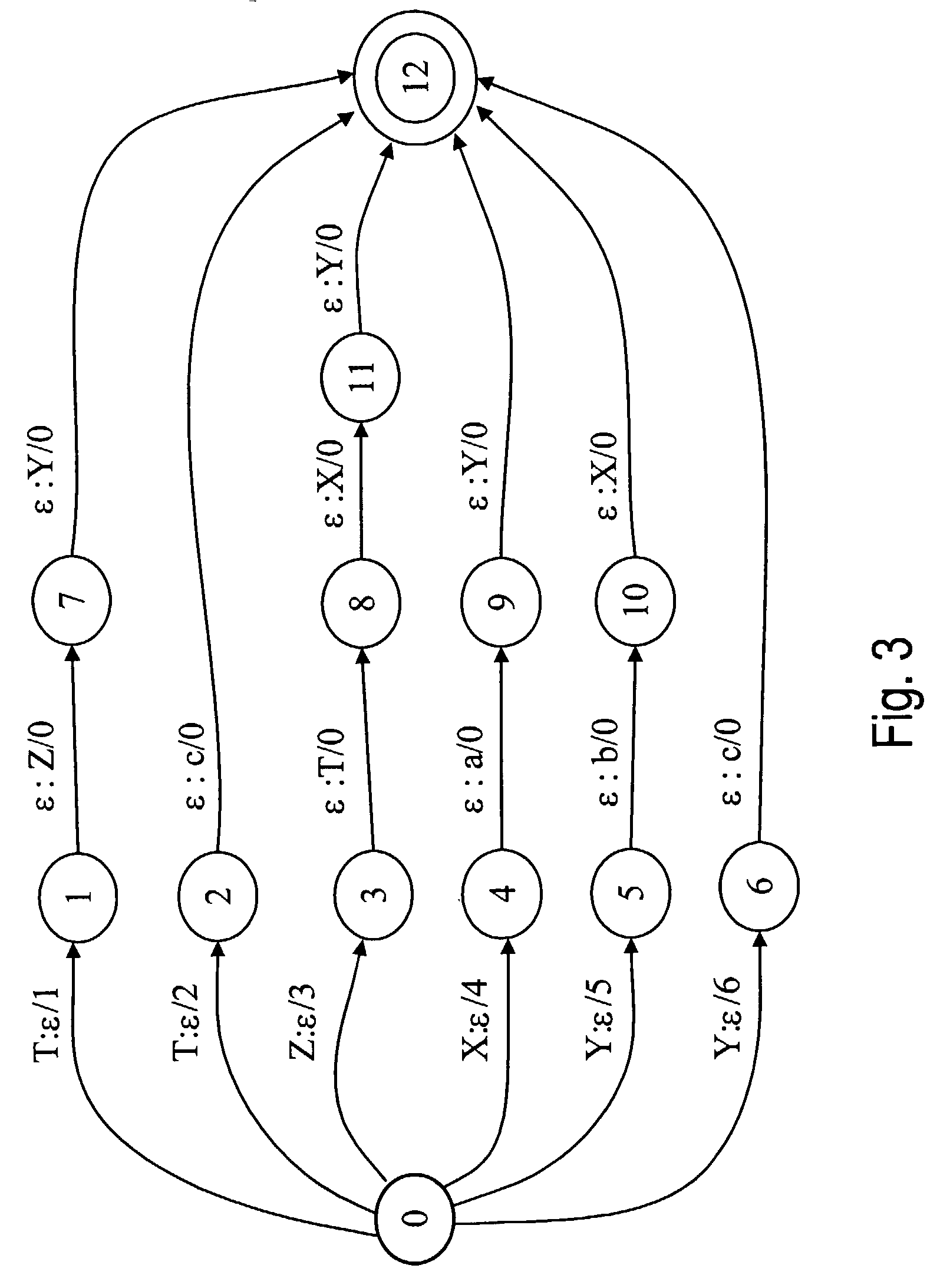
A context-free grammar can be represented by a weighted finite-state transducer. This representation can be used to efficiently compile that grammar into a weighted finite-state automaton that accepts the strings allowed by the grammar with the corresponding weights. The rules of a context-free grammar are input. A finite-state automaton is generated from the input rules. Strongly connected components of the finite-state automaton are identified. An automaton is generated for each strongly connected component. A topology that defines a number of states, and that uses active ones of the non-terminal symbols of the context-free grammar as the labels between those states, is defined. The topology is expanded by replacing a transition, and its beginning and end states, with the automaton that includes, as a state, the symbol used as the label on that transition. The topology can be fully expanded or dynamically expanded as required to recognize a particular input string.
Owner:NUANCE COMM INC
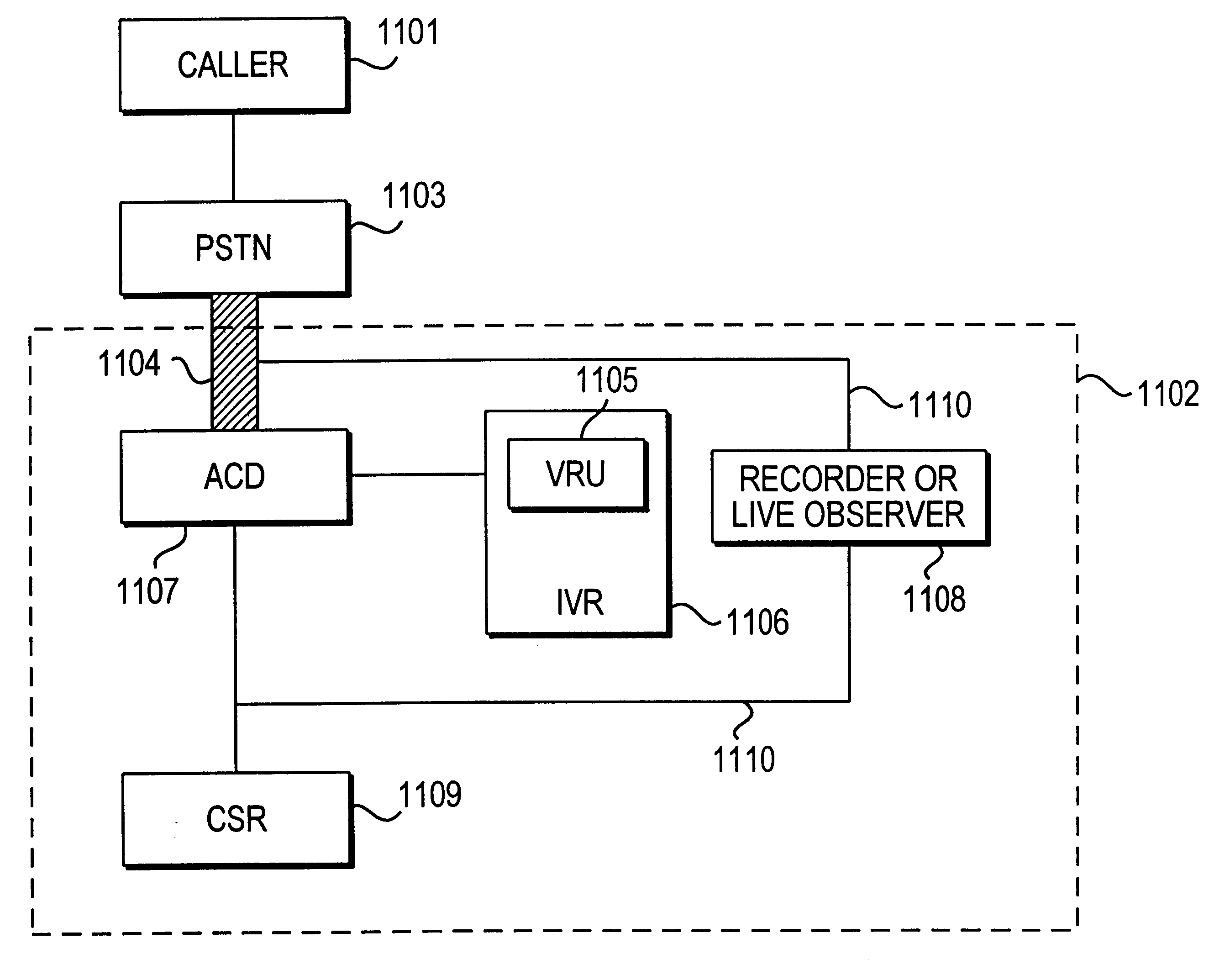
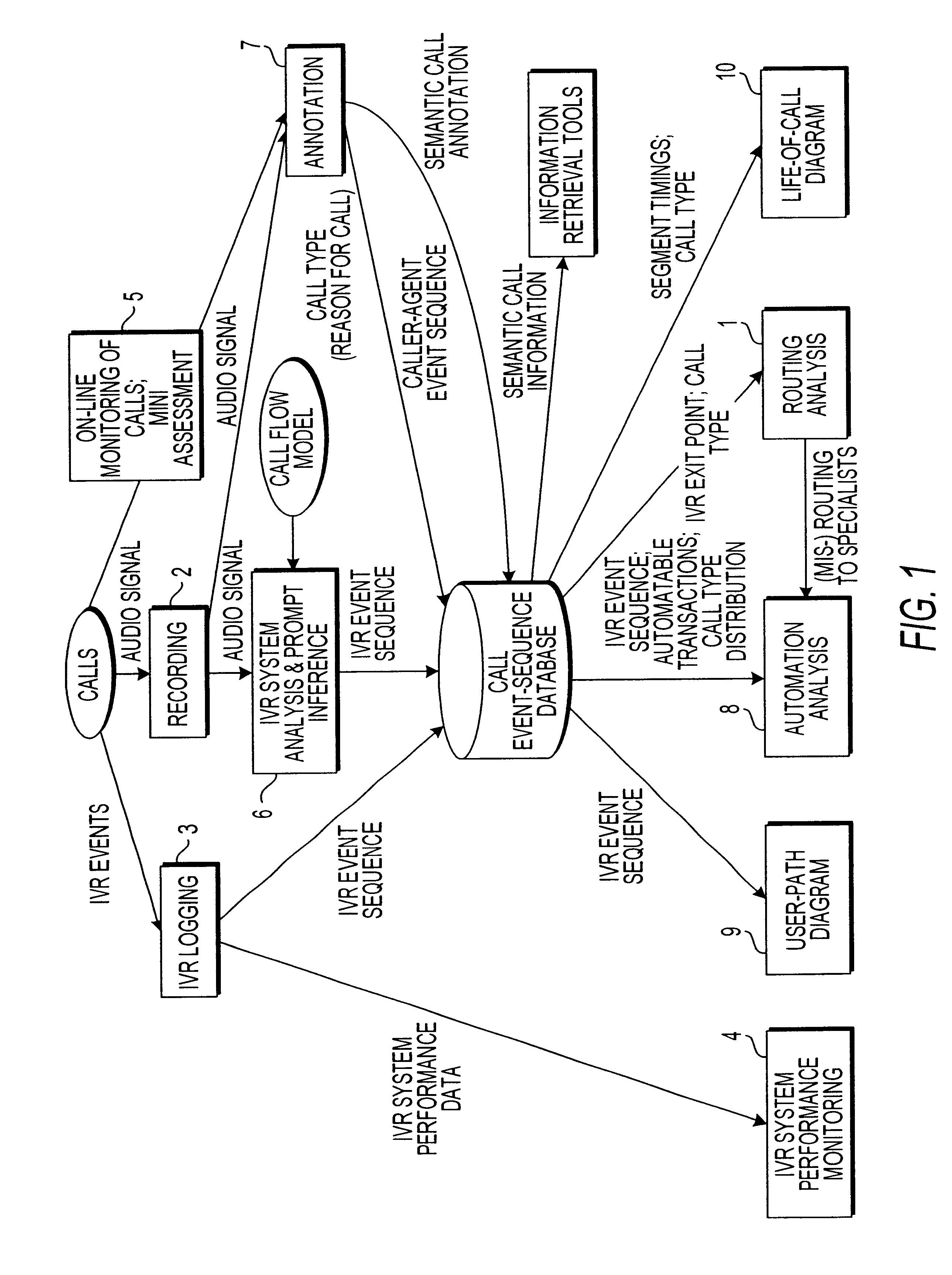
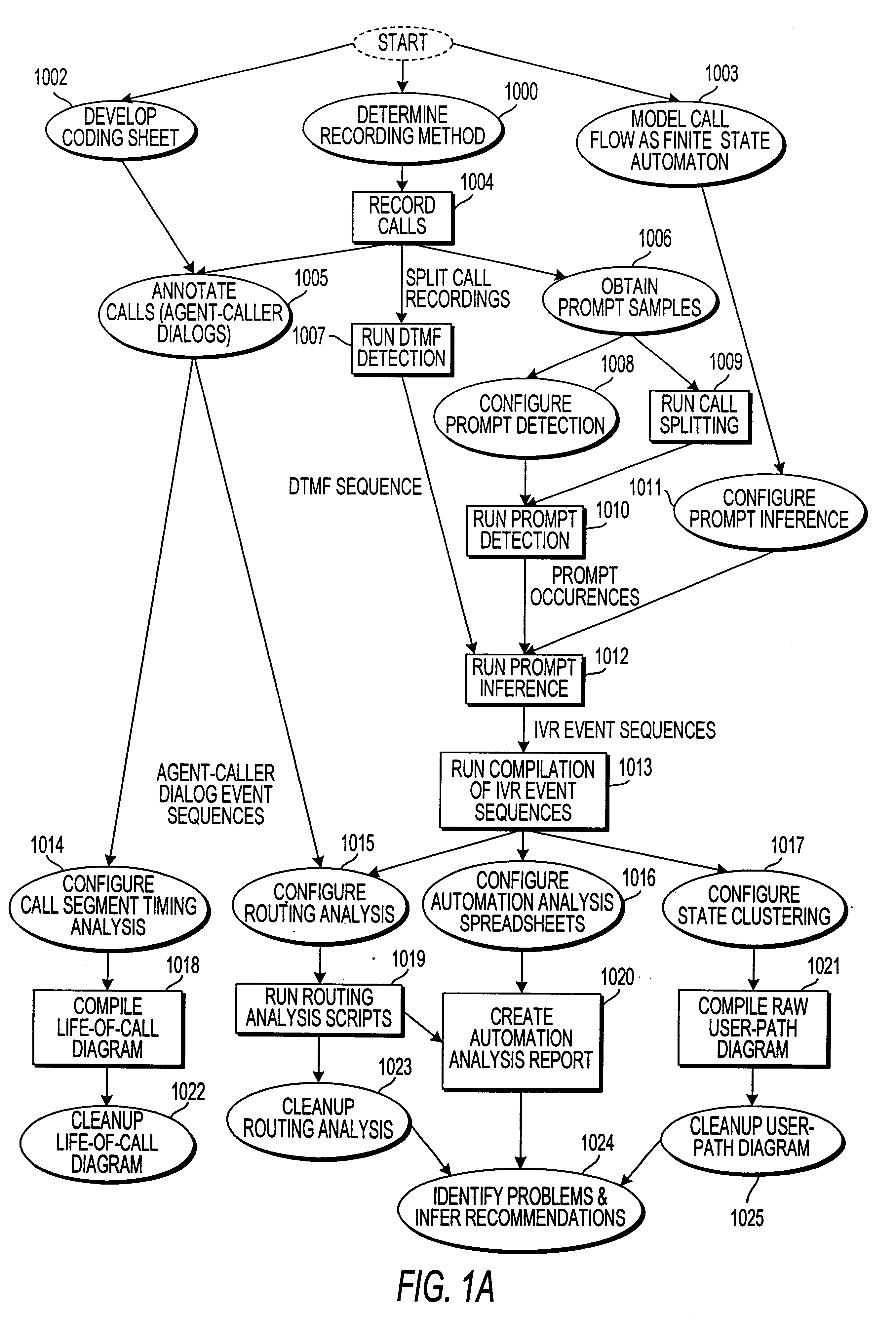
Apparatus and method for analyzing an automated response system
InactiveUS6823054B1Automatic call-answering/message-recording/conversation-recordingSpecial service for subscribersSpeech inputAutomaton
A system for analyzing an interactive voice response (IVR) system of a call processing center determines a complete sequence of events occurring within the IVR system. The IVR system being operable to automatically accept calls from callers and respond to input from the callers. The system models a call flow of the IVR system as a non-deterministic finite-state automaton. A recording of a plurality of calls to the call processing center is split, such that each of plural calls to the call center is in one audio file. For a plurality of calls, the system detects a complete sequence of DTMF and / or speech input to the IVR system, detects selected prompts issued by the IVR system, and inputs the detected sequence of DTMF and / or speech input as well as the detected prompts issued by the IVR system into the finite-state automaton to determine a call-event sequence for that call. The call-event sequence includes information regarding how that call left the IVR system.
Owner:VERIZON PATENT & LICENSING INC +1
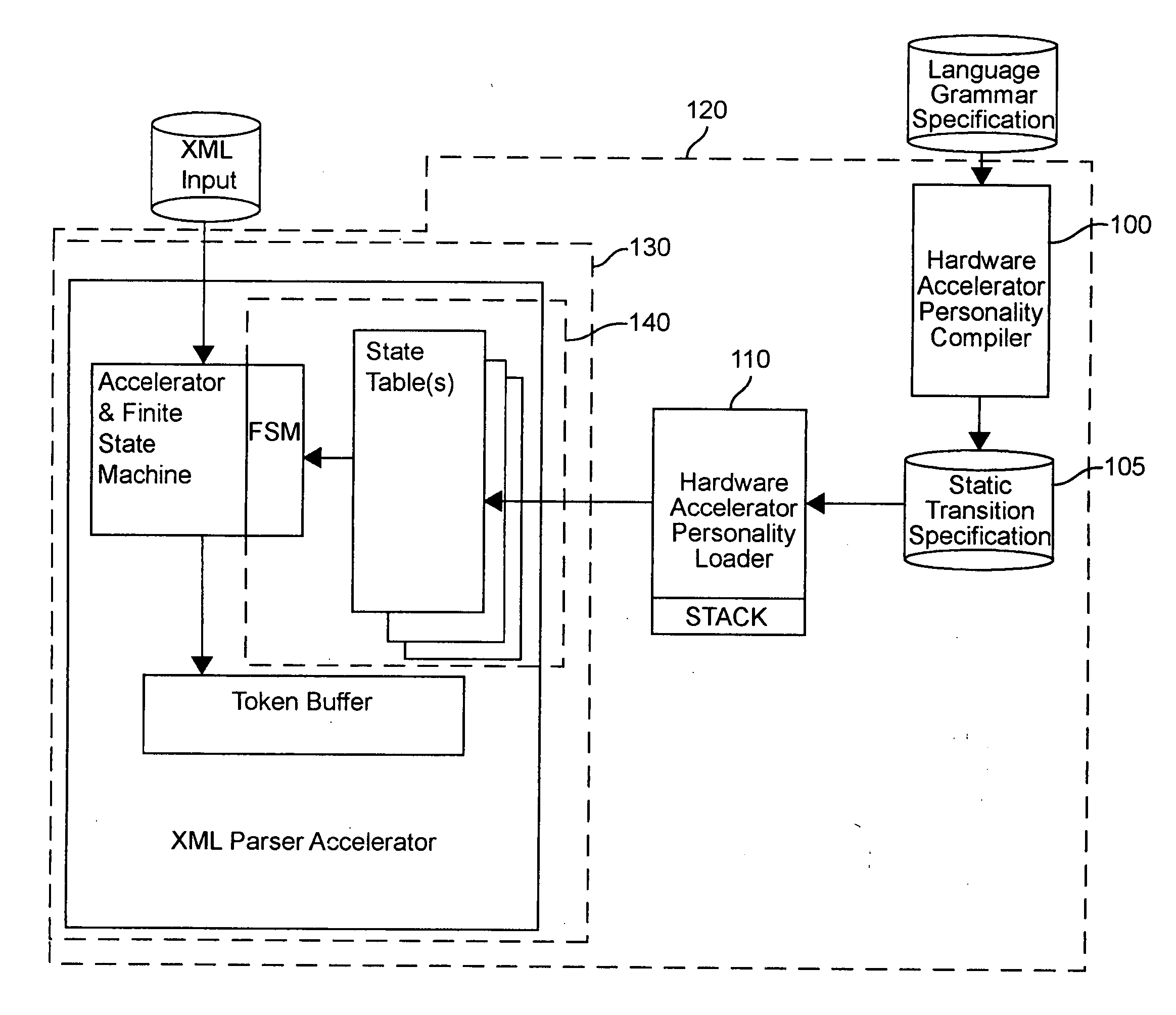
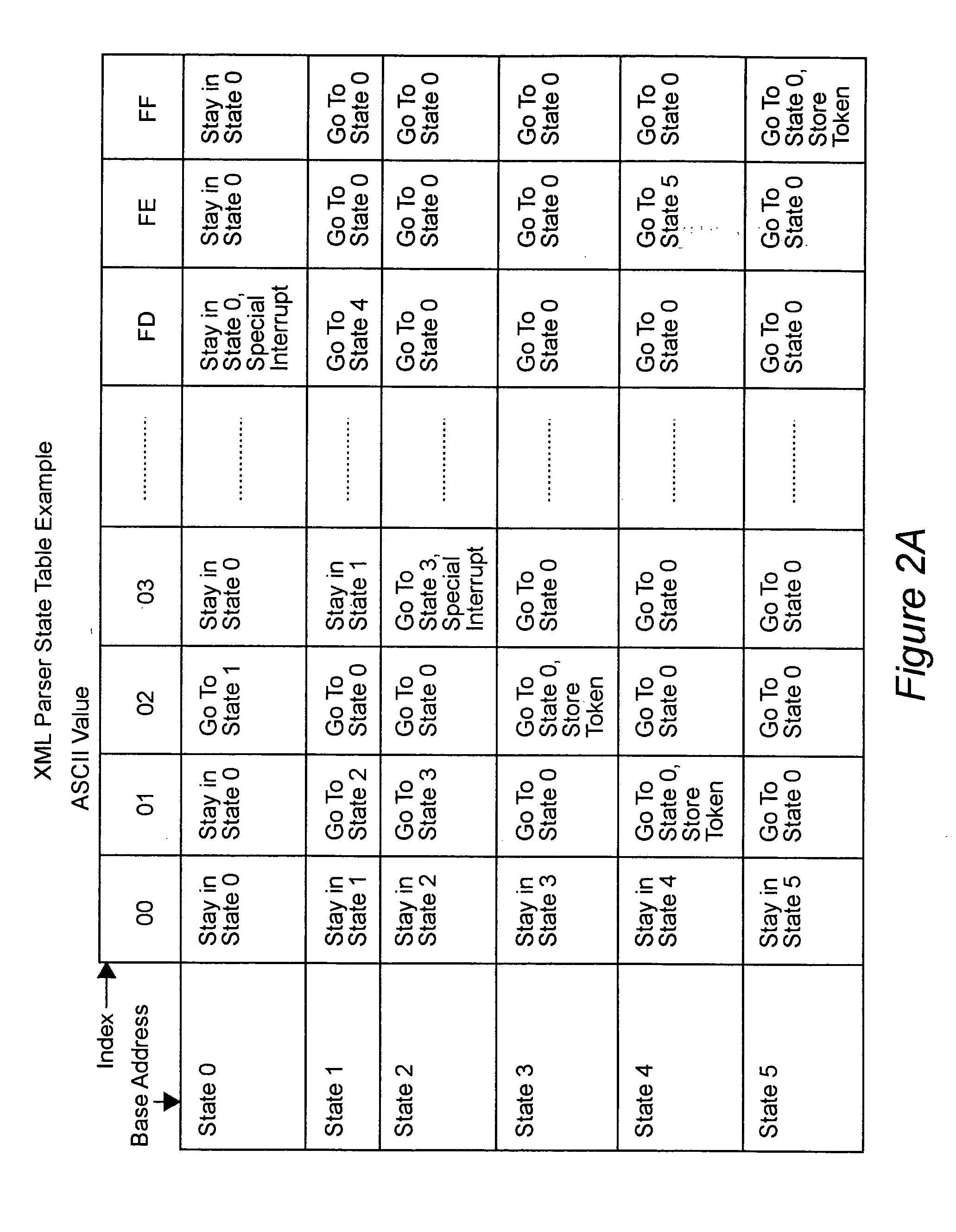
Hardware accelerator personality compiler
InactiveUS20040172234A1Software engineeringSpecial data processing applicationsState switchingAutomaton
Error-free state tables are automatically generated from a specification of a group of desired performable functions, such as are provided in a programming language in a formal notation such as Backus-Naur form or a derivative thereof by discriminating tokens corresponding to respective performable functions, identifications, arguments, syntax, grammar rules, special symbols and the like. The tokens may be recursive (e.g. infinite), in which case they are transformed into a finite automata which may be deterministic or non-deterministic. Non-deterministic finite automata are transformed into deterministic finite automata and then into state transitions which are used to build a state table which can then be stored or, preferably, loaded into a finite state machine of a hardware parser accelerator to define its personality.
Owner:LOCKHEED MARTIN CORP
High speed data stream pattern recognition
InactiveUS6856981B2Increase speedLow memory storage requirementDigital data information retrievalMultiple digital computer combinationsData streamState dependent
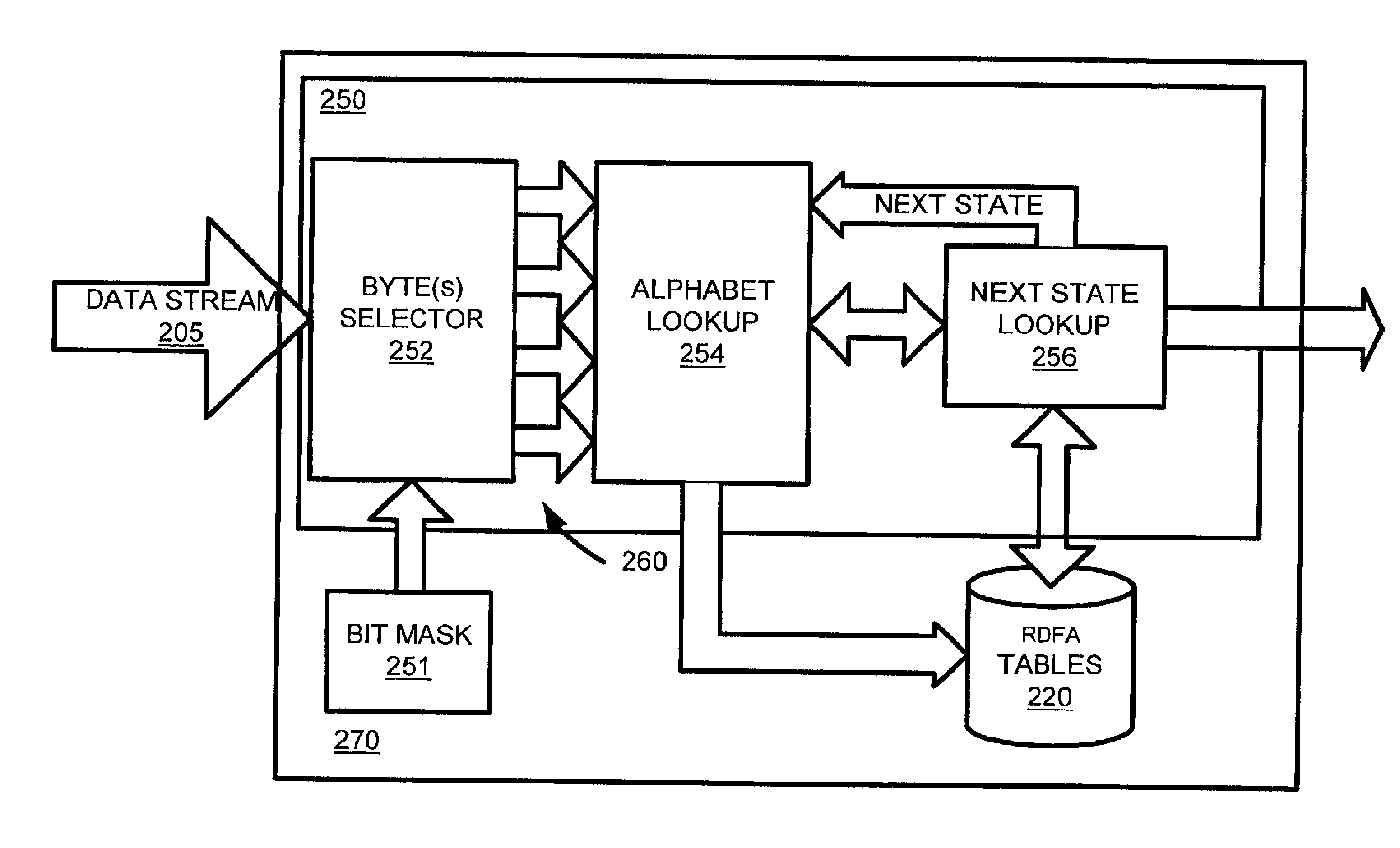
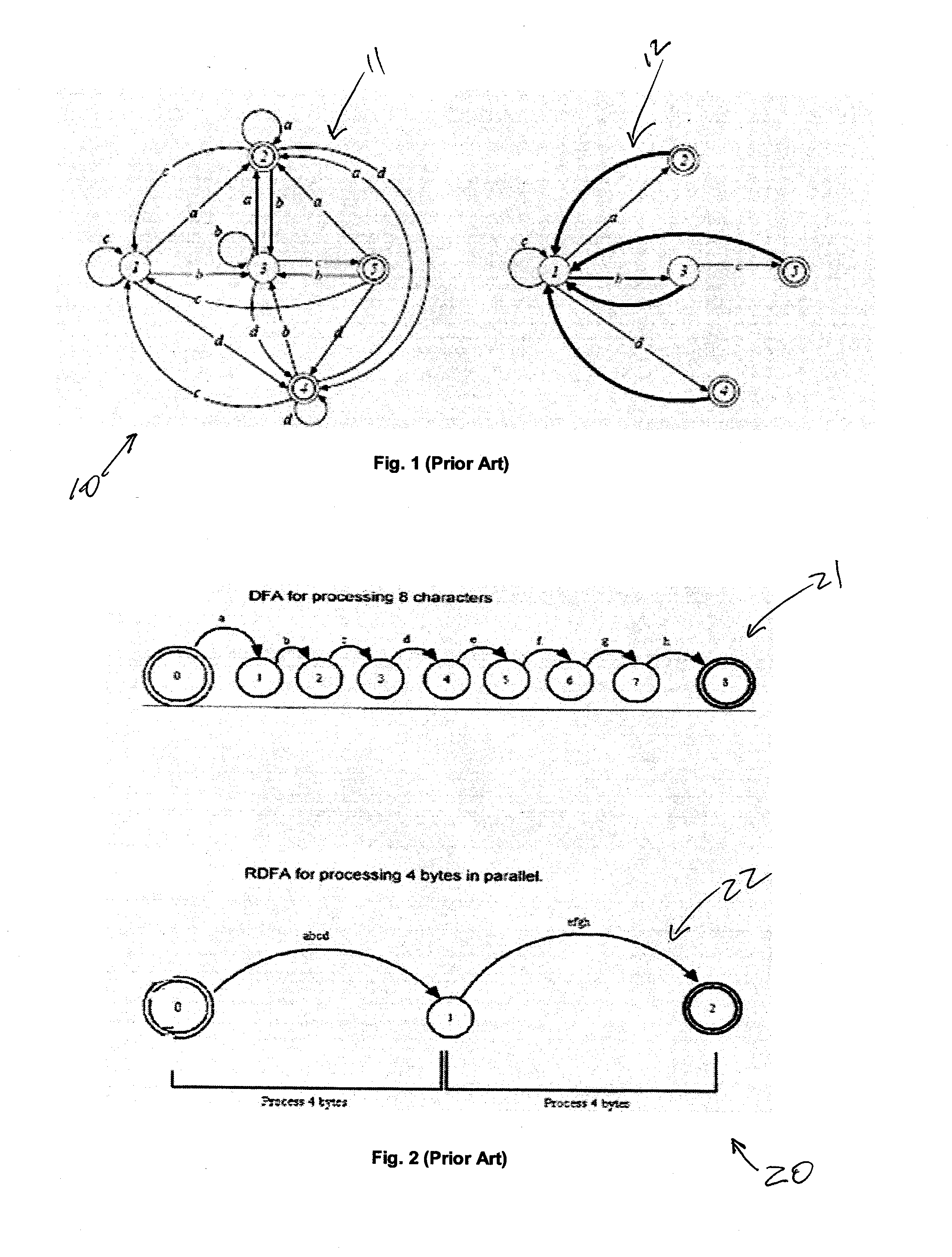
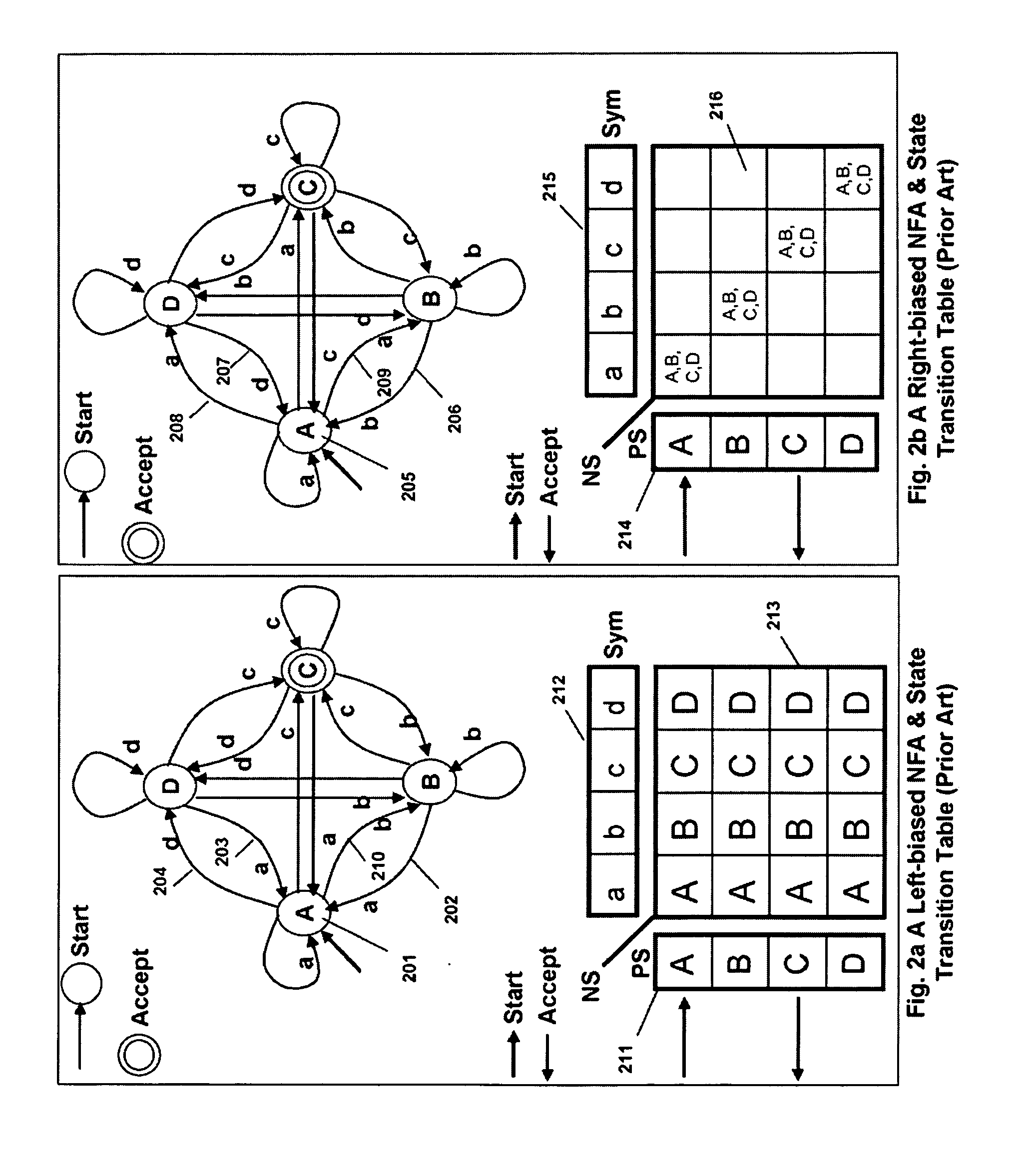
A system and method in accordance with the present invention determines in real-time the portions of a set of characters from a data or character stream which satisfies one or more predetermined regular expressions. A Real-time Deterministic Finite state Automaton (RDFA) ensures that the set of characters is processed at high speeds with relatively small memory requirements. An optimized state machine models the regular expression(s) and state related alphabet lookup and next state tables are generated. Characters from the data stream are processed in parallel using the alphabet lookup and next state tables, to determine whether to transition to a next state or a terminal state, until the regular expression is satisfied or processing is terminated. Additional means may be implemented to determine a next action from satisfaction of the regular expression.
Owner:RAMBUS INC
Fast and scalable process for regular expression search
InactiveUS20080034427A1Reducing required for pattern matchingReducing deterministic finite automata (DFA)Memory loss protectionError detection/correctionPattern matchingAutomaton
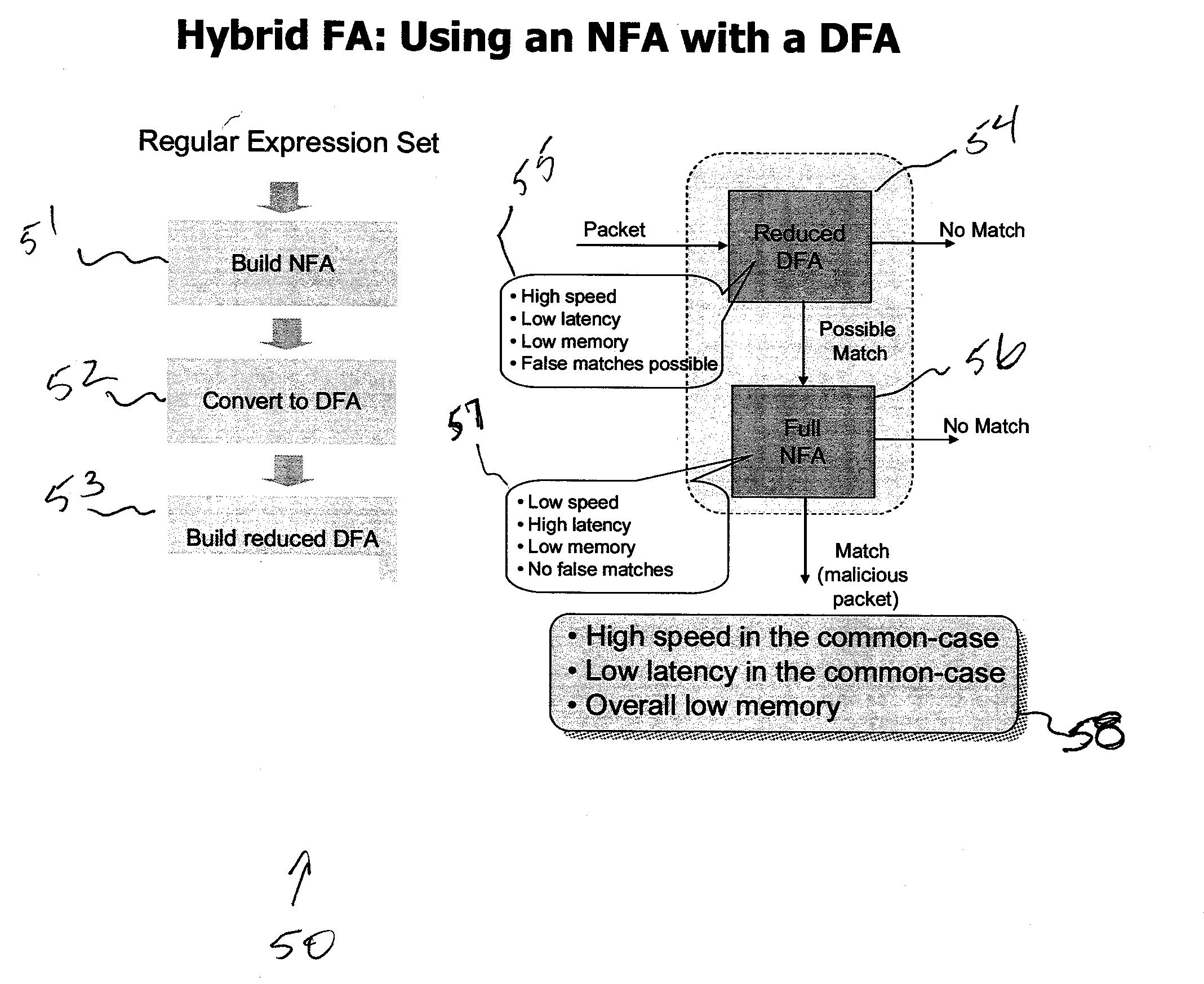
A method includes reducing a deterministic finite automata DFA representative of an expression to provide a smaller DFA, and subjecting information that matches the smaller DFA to non-deterministic finite automata NFA representative of the expression for reducing memory required for pattern matching of the information.
Owner:NEC LAB AMERICA
Complex symbol evaluation for programmable intelligent search memory
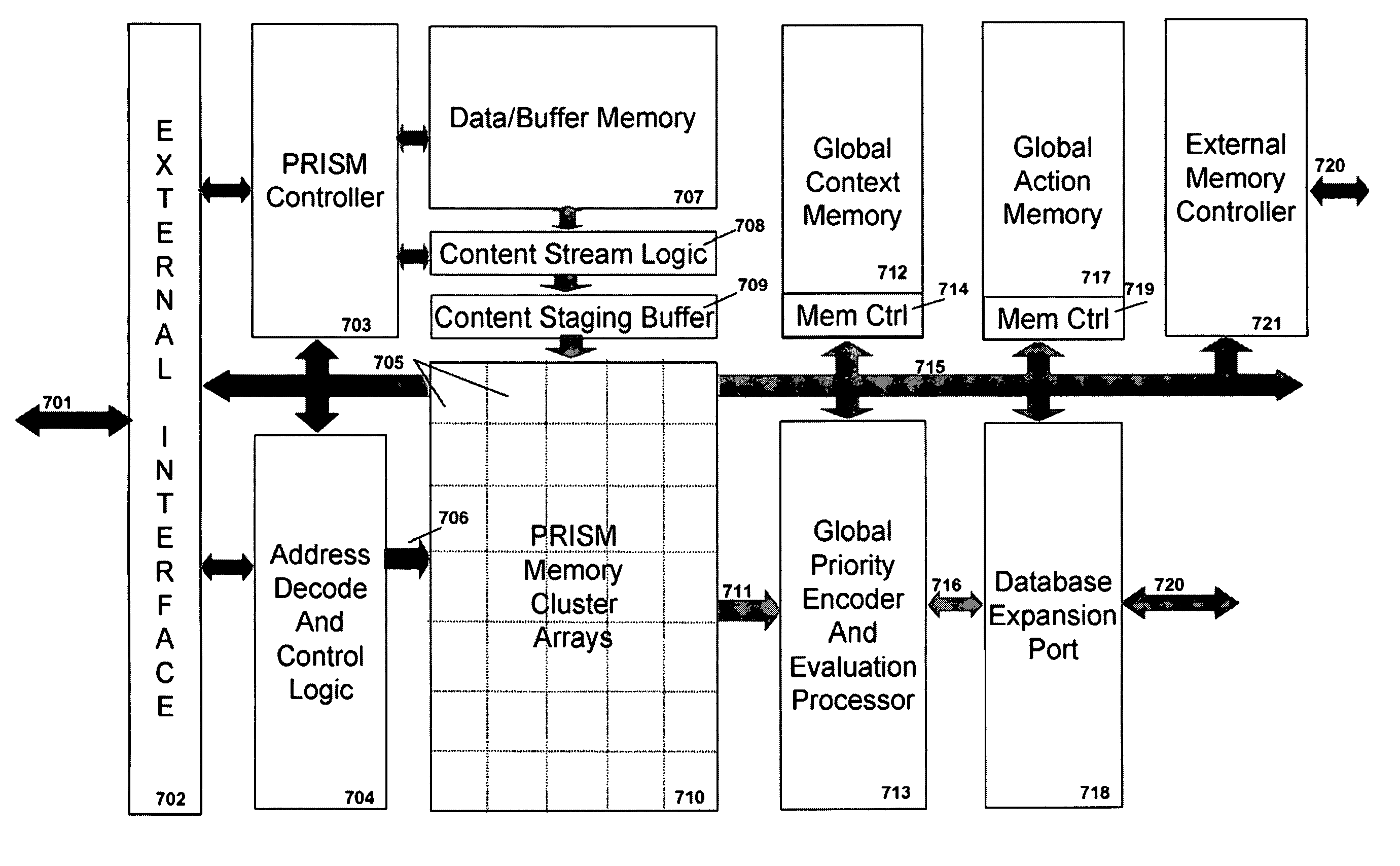
ActiveUS7827190B2Efficient and compact realizationDigital data information retrievalDigital data processing detailsTerm memoryMemory architecture
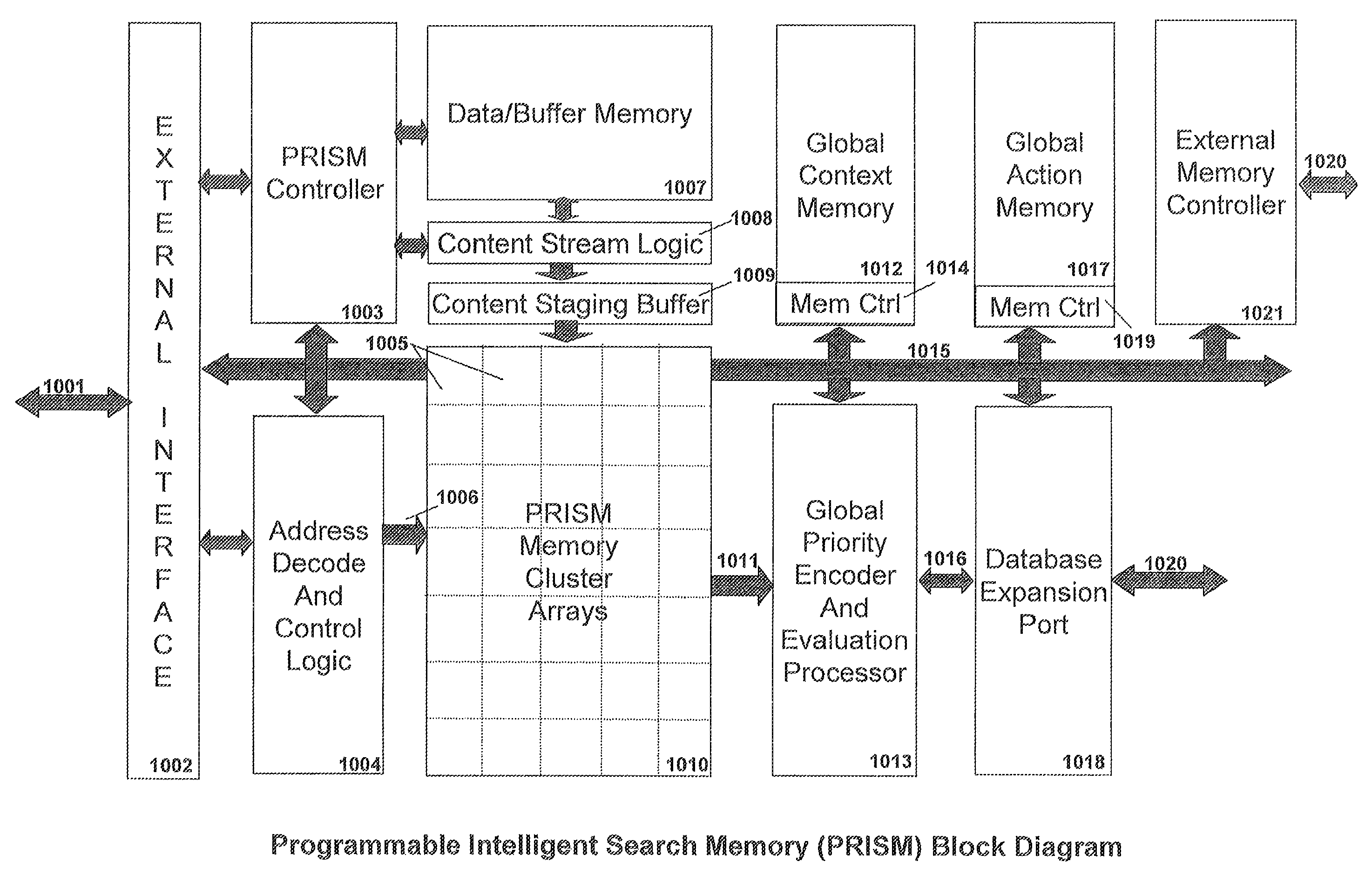
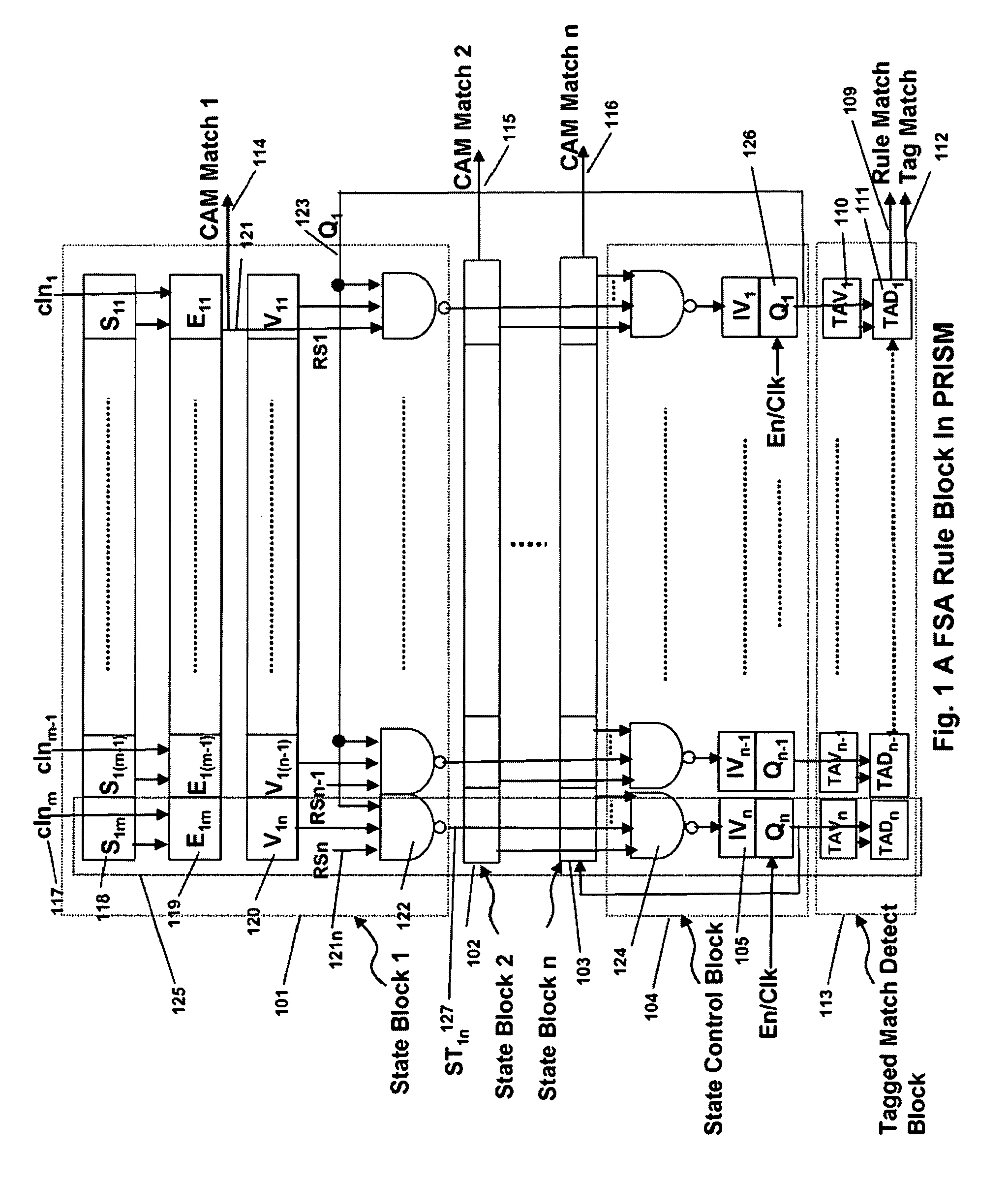
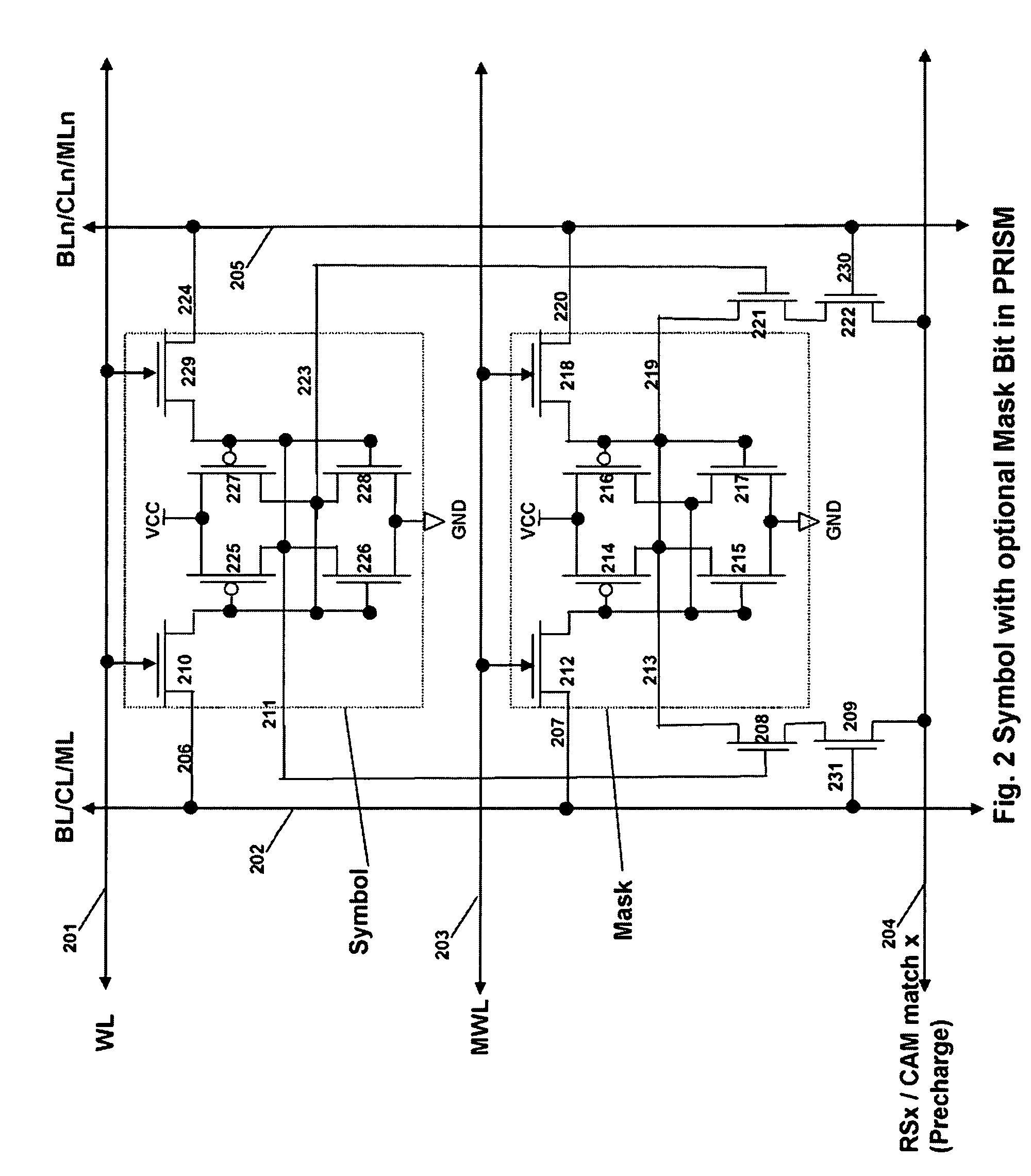
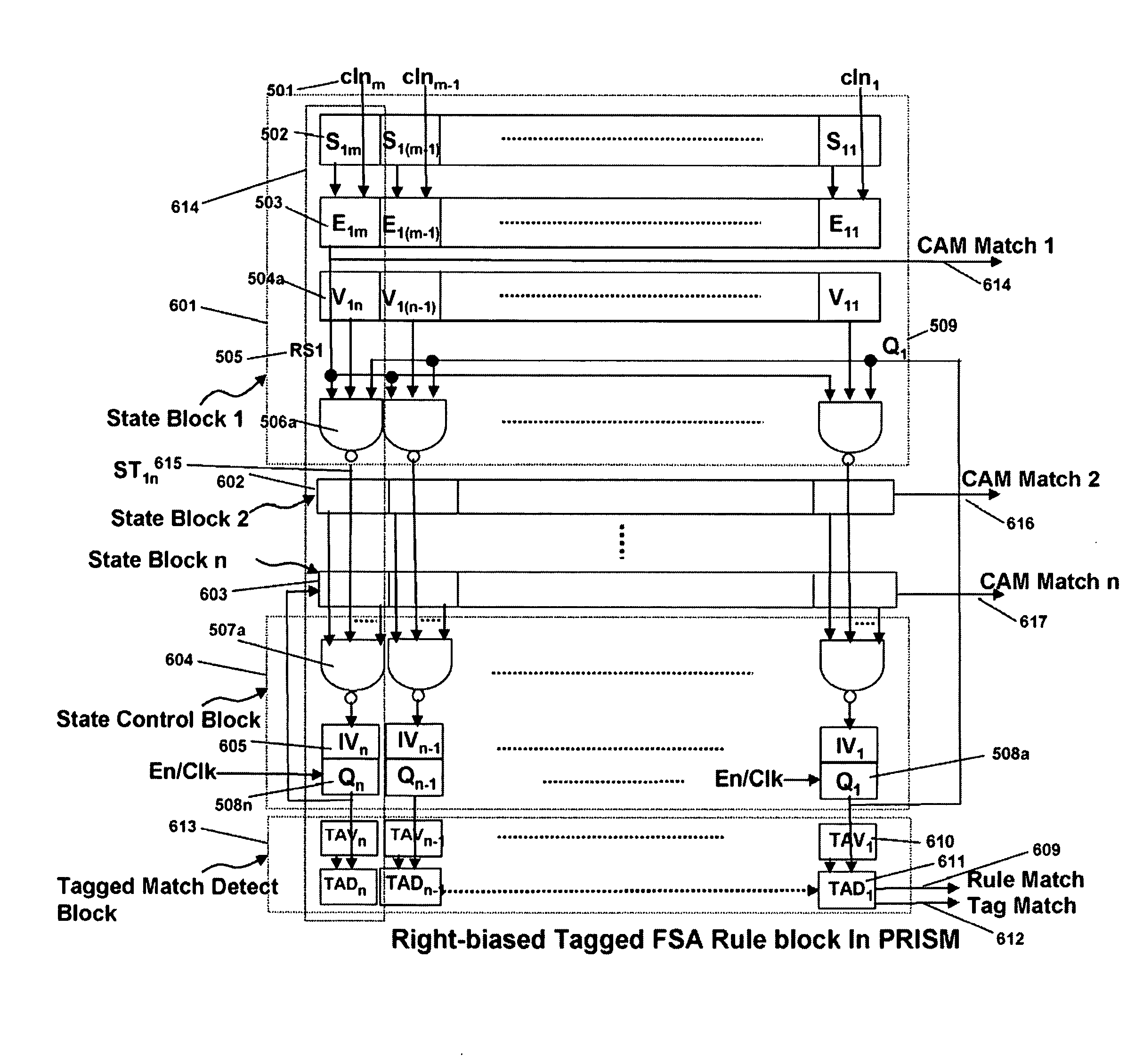
Memory architecture provides capabilities for high performance content search. The architecture creates an innovative memory that can be programmed with content search rules which are used by the memory to evaluate presented content for matching with the programmed rules. When the content being searched matches any of the rules programmed in the Programmable Intelligent Search Memory (PRISM) action(s) associated with the matched rule(s) are taken. Content search rules comprise of regular expressions which are converted to finite state automata and then programmed in PRISM for evaluating content with the search rules. The PRISM memory provides features for complex regular expression symbols like range detection, complement control, bit masking and the like and enables complex symbols and compact regular expression representation.
Owner:INFOSIL INC
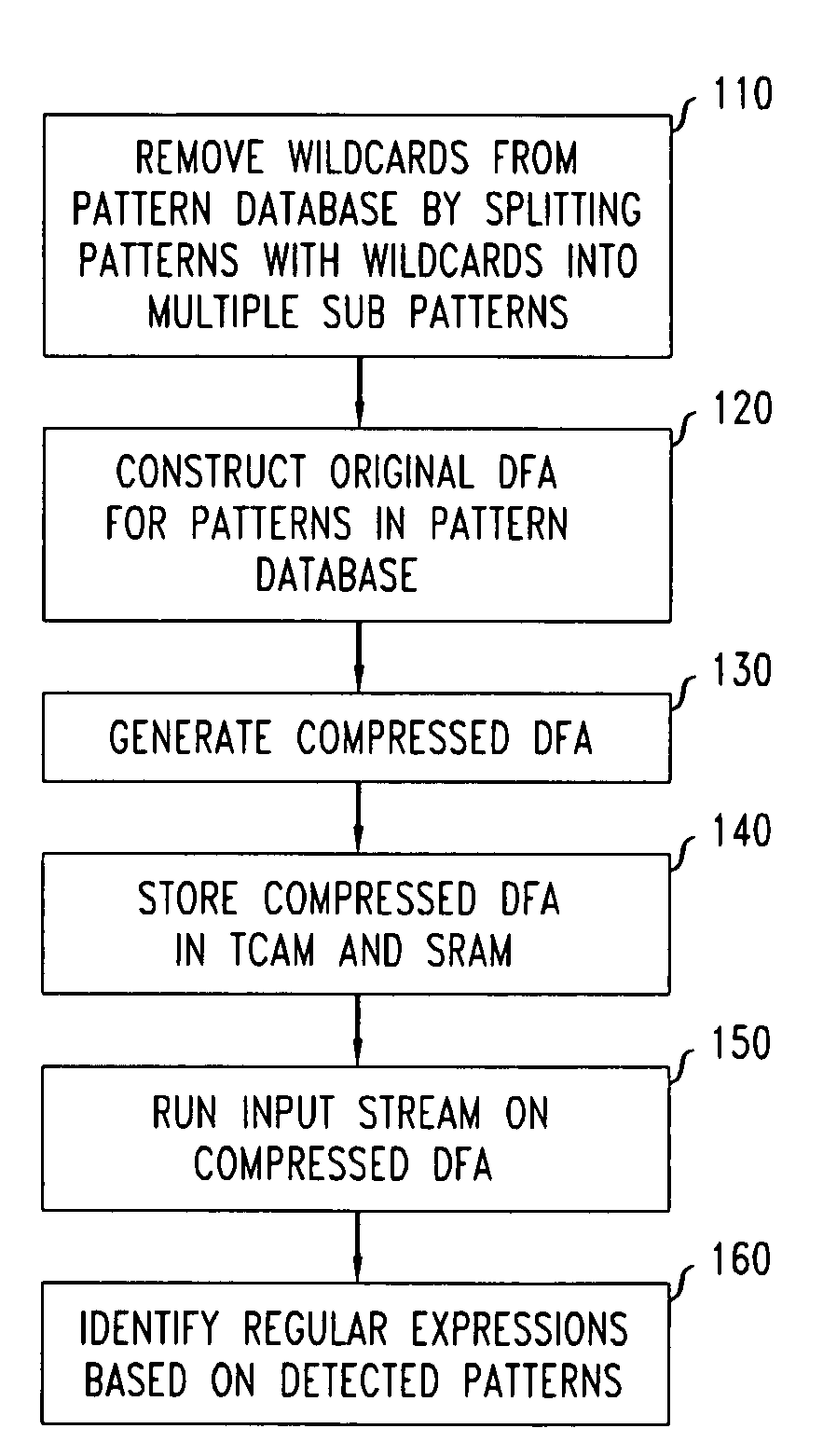
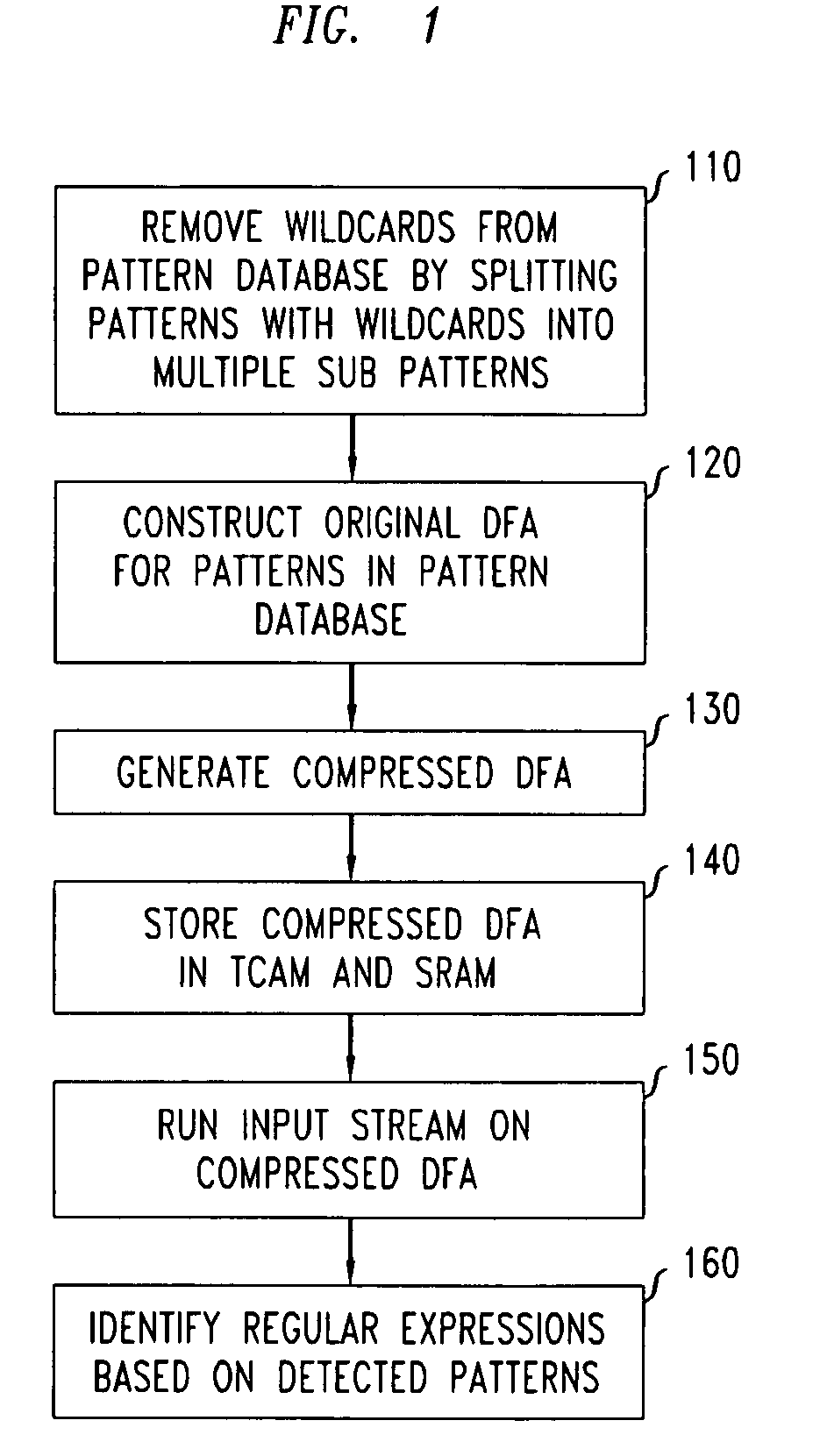
Method and system for multi-character multi-pattern pattern matching
ActiveUS20080046423A1High pattern matching speedEasy to implementData processing applicationsDigital data information retrievalPattern matchingTernary content addressable memory
Disclosed is a method and system for multi-character multi-pattern pattern matching. In the multi-character multi-pattern pattern matching method, patterns in an input stream are detected by transitioning between states of a “compressed deterministic finite state automaton (DFA)”, with each transition based on multiple characters of the input stream. The compressed DFA is created by compressing an original DFA, such as an Aho-Corasick DFA, such that each state of the compressed DFA represents multiple consecutive states of the original DFA and each transition between the states of the compressed DFA is a combination of all of the transitions between the multiple consecutive states of the original DFA. This method can be implemented using a Ternary Content-Addressable Memory (TCAM) to store the transitions of the compressed DFA and compares the transitions with multiple characters of an input stream at a time to detect patterns in the input stream.
Owner:ALGOGENE FINANCIAL TECHNOLOGY COMPANY LIMITED
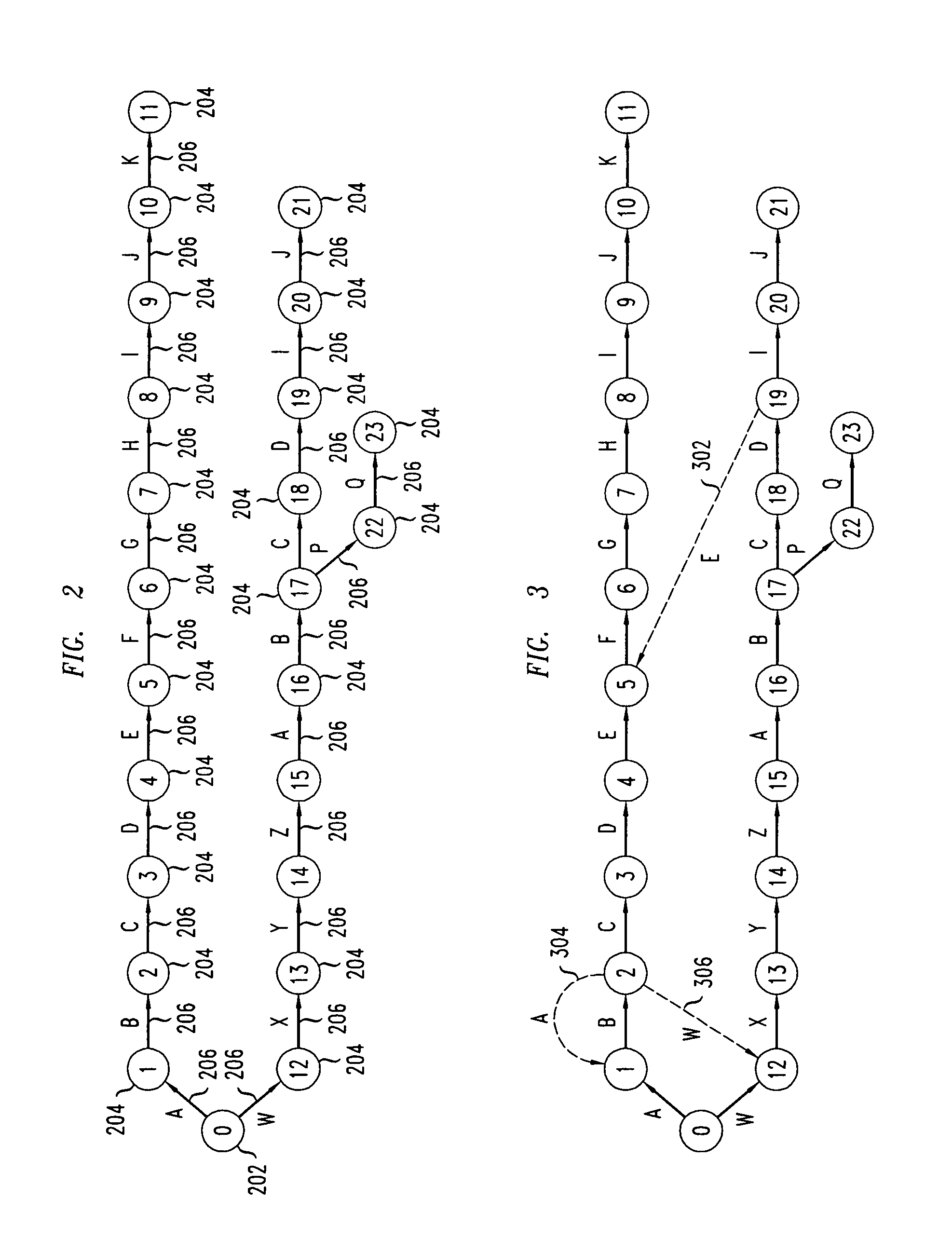
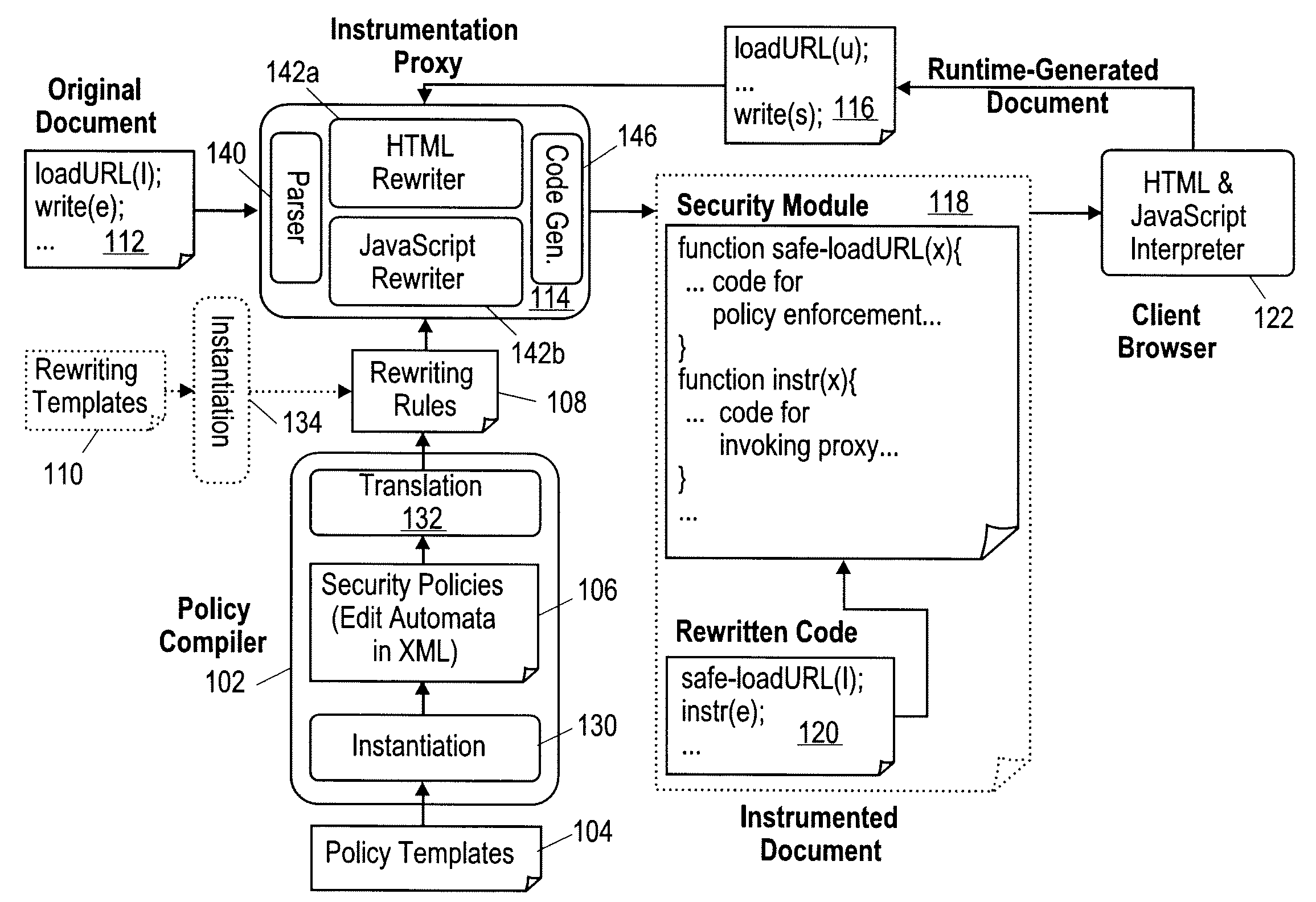
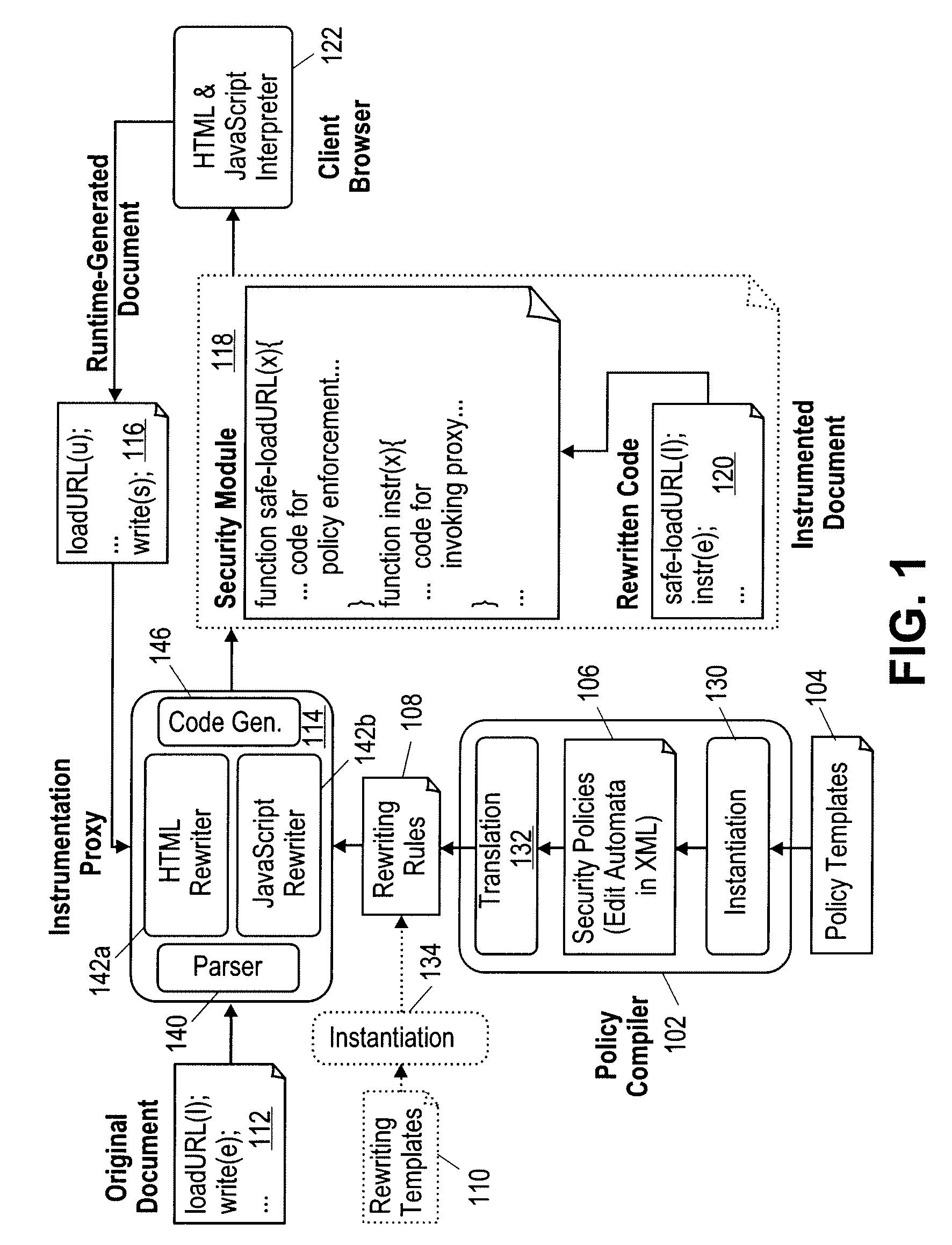
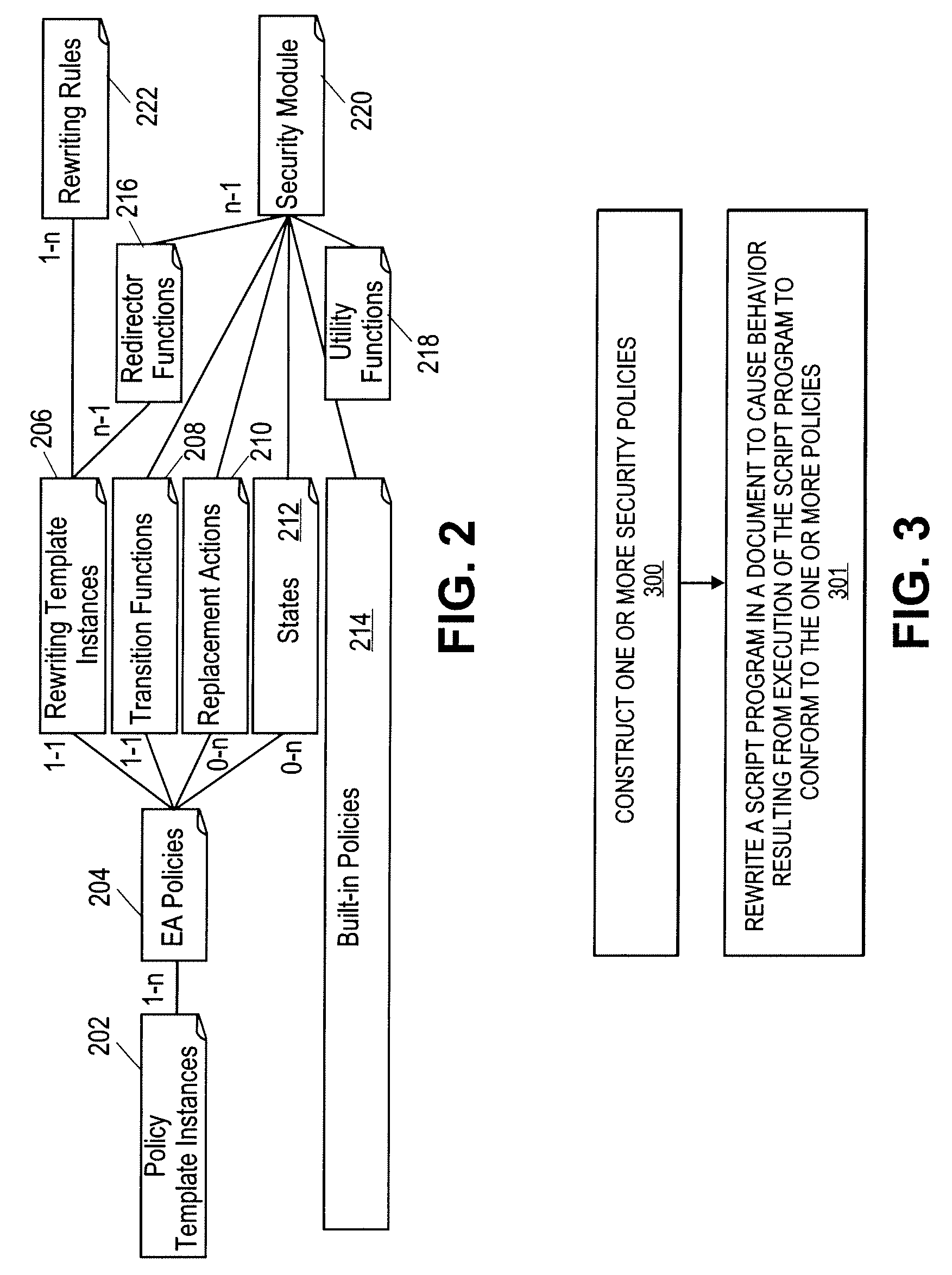
Method and apparatus for constructing security policies for web content instrumentation against browser-based attacks
A method and apparatus is disclosed herein for constructing security policies for content instrumentation against attacks. In one embodiment, the method comprises constructing one or more security policies for web content using at least one rewriting template, at least one edit automata policy, or at least one policy template; and rewriting a script program in a document to cause behavior resulting from execution of the script to conform to the one or more policies.
Owner:NTT DOCOMO INC
Memory circuit for aho-corasick type character recognition automaton and method of storing data in such a circuit
ActiveUS20070075878A1Number of bitDigital data information retrievalCode conversionMemory addressData stream
A memory circuit for an Aho-Corasick type character recognition automaton uses a node tree for recognizing predetermined strings of characters in an incoming data stream. The recognization is based upon successive transitions in the node tree stored in memory in which each node corresponds to a recognized sequence of a character string. At least part of the nodes are related to a consecutive node by a valid transition, from an initial state to terminal states, with each one corresponding to a recognized character string This memory circuit includes first sets of consecutive memory addresses defining respectively strings of consecutive nodes accessible sequentially during successive transitions to a terminal state, and second sets of memory addresses defining multiple nodes each pointing to several states.
Owner:STMICROELECTRONICS SRL
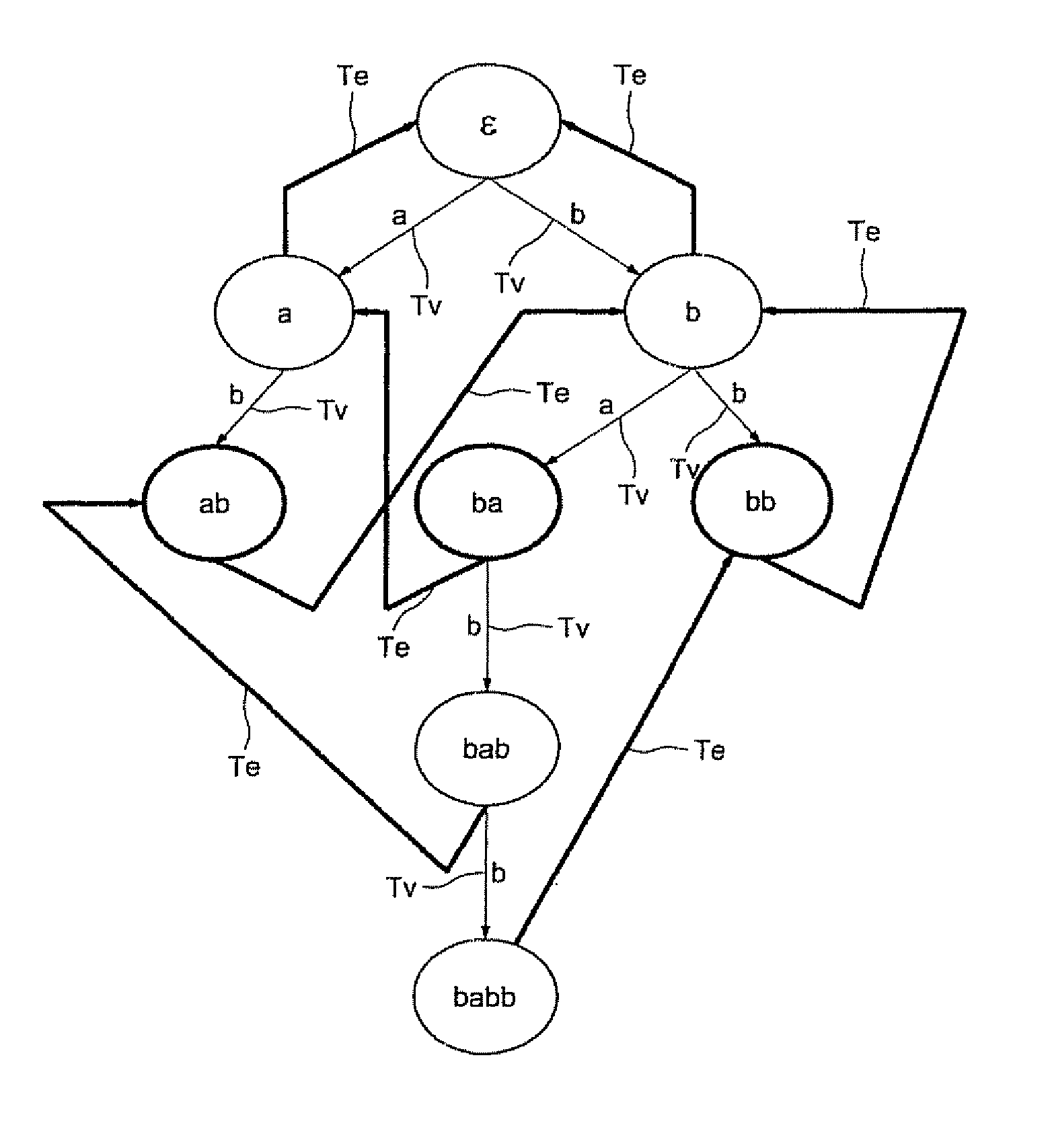
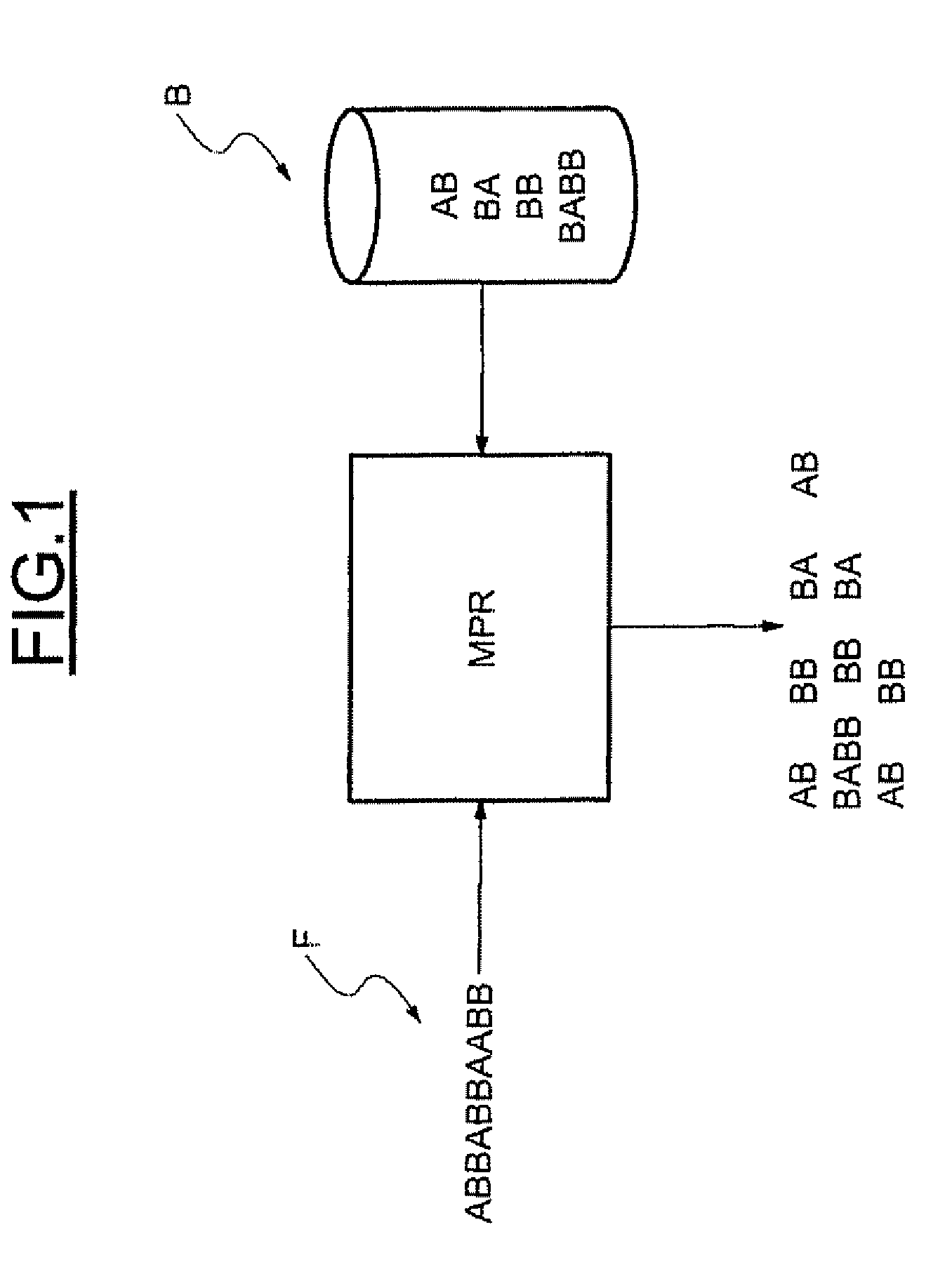
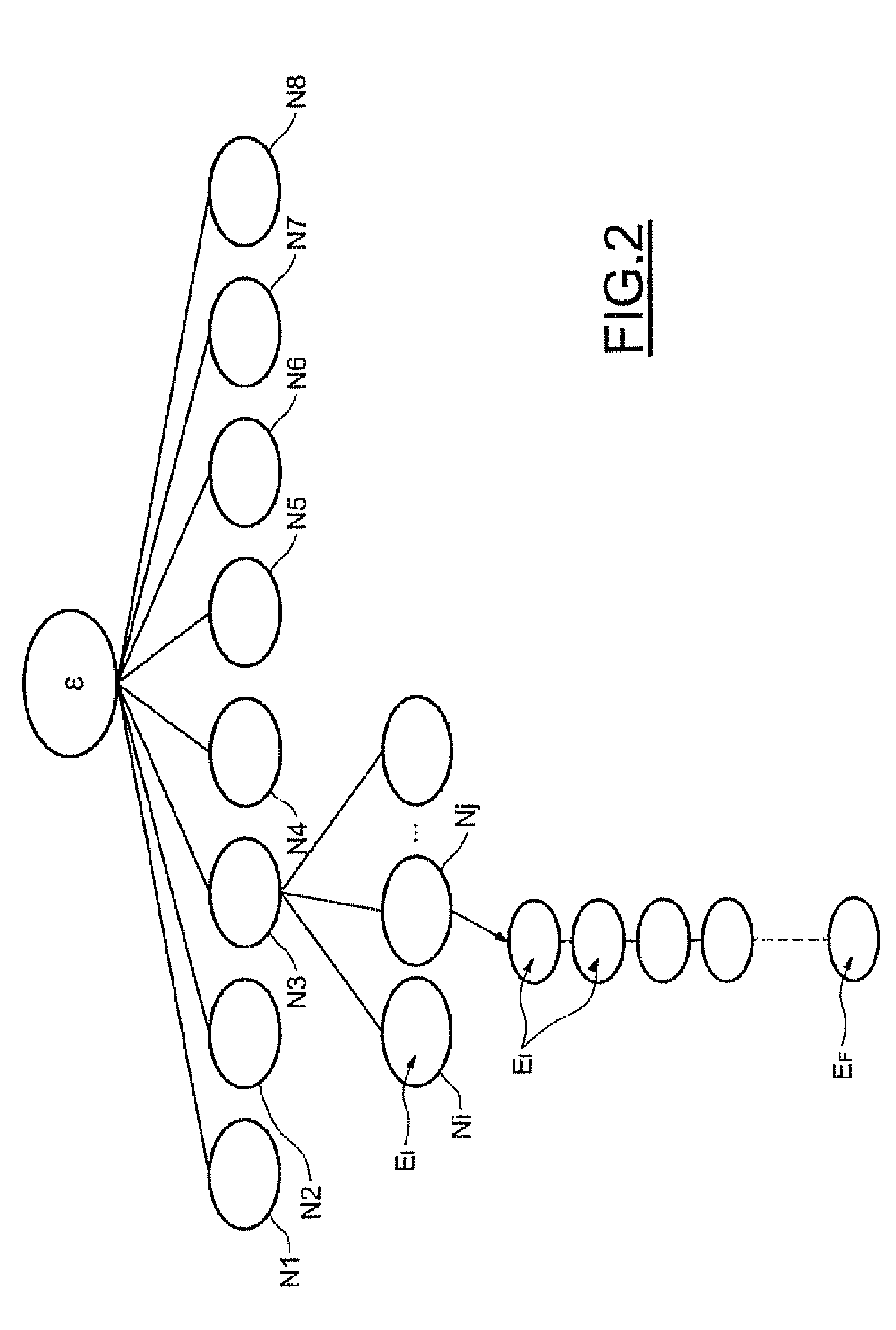
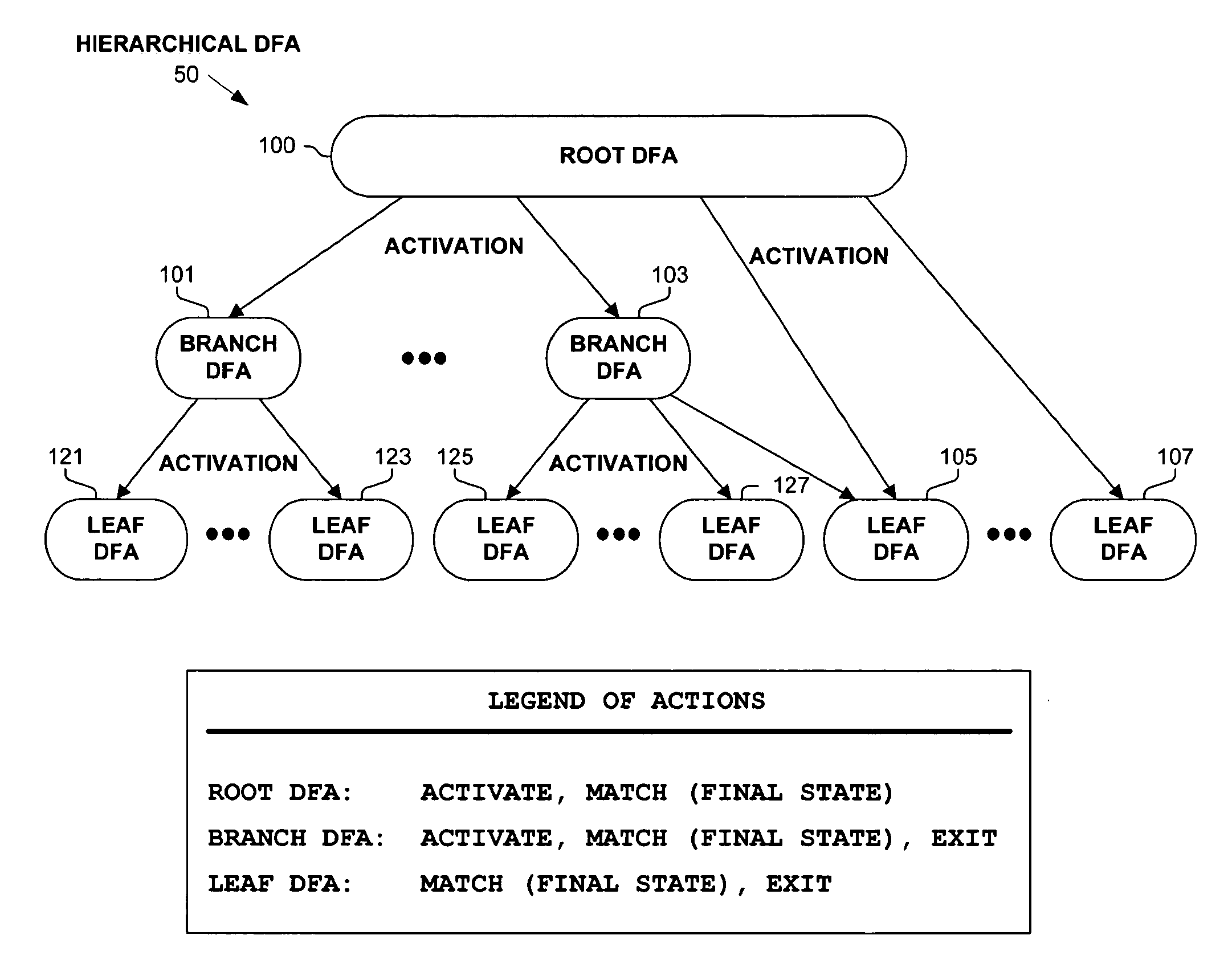
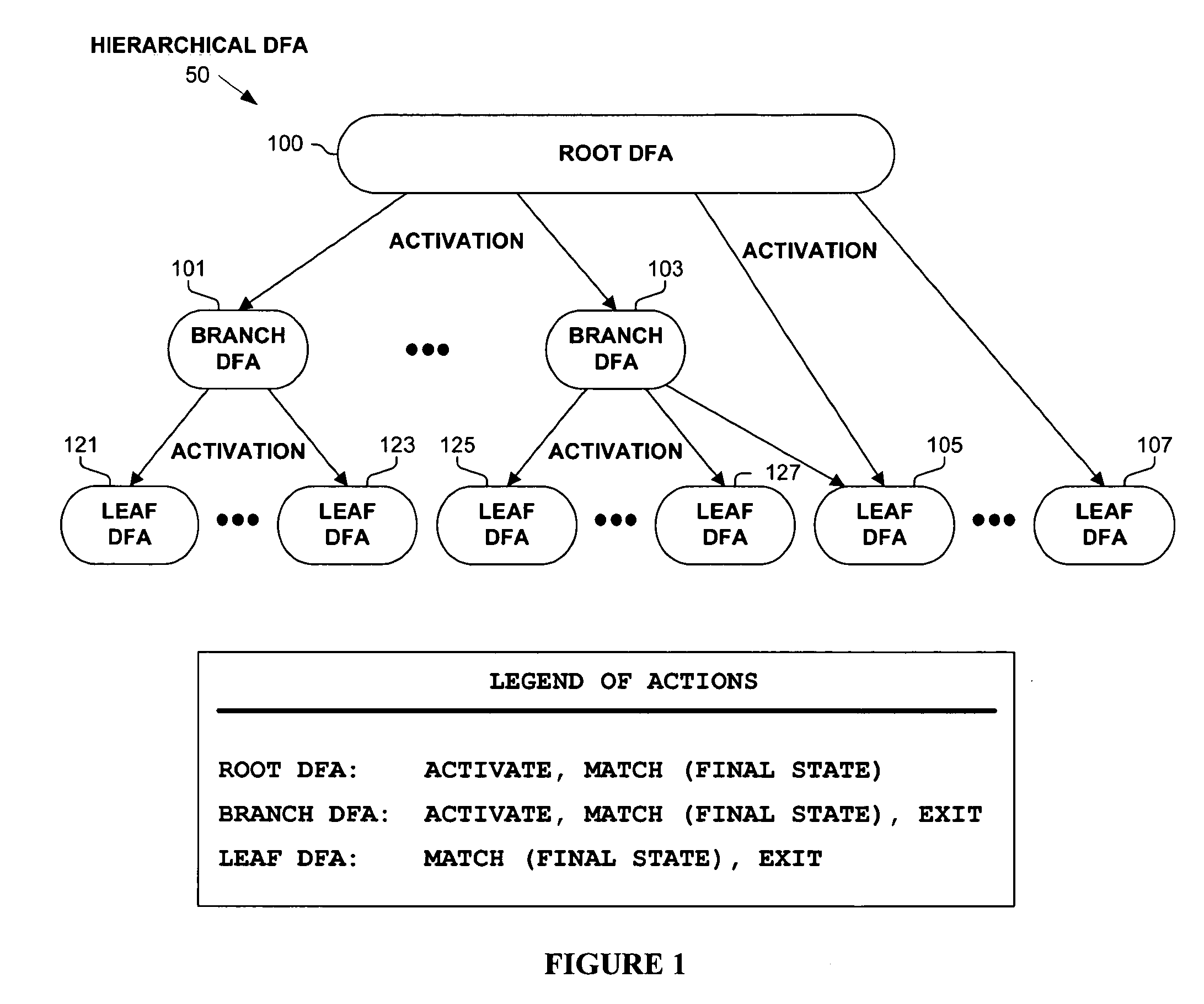
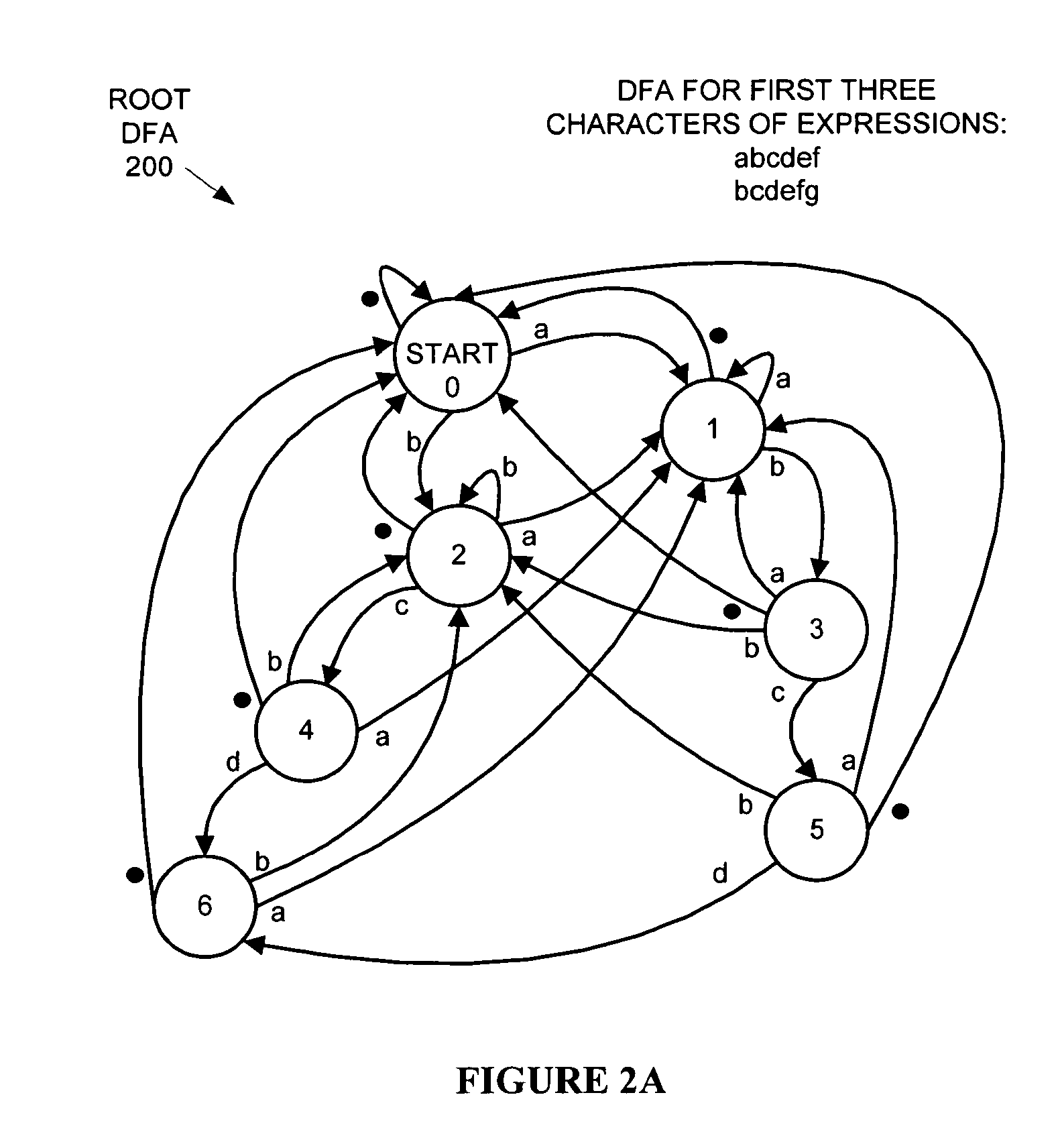
Hierarchical tree of deterministic finite automata
ActiveUS20060242123A1Avoid explosionDigital data information retrievalDigital data processing detailsBiological activationAutomaton
A hierarchical tree of deterministic finite automata (DFA) is traversed and / or generated based on a set of regular expressions. The hierarchical DFA includes a root DFA linked together with a set of leaf DFAs, and possibly a set of branch DFAs. The root DFA is always active and is responsive to an input string, as are any currently active branch and leaf DFAs. When a final state or arc is reached or traversed in any active DFA, a regular expression has been matched. The branch and leaf DFAs are activated in response to the root DFA or a branch DFA reaching or traversing an activation state or arc corresponding to the branch or leaf DFA. Active branch and leaf DFAs will become inactive when a termination state or arc is reached or traversed within the branch or leaf DFA. State explosion in the hierarchical DFA can typically be avoided by selectively grouping similar portions of the regular expressions together in branch and leaf DFAs.
Owner:CISCO TECH INC
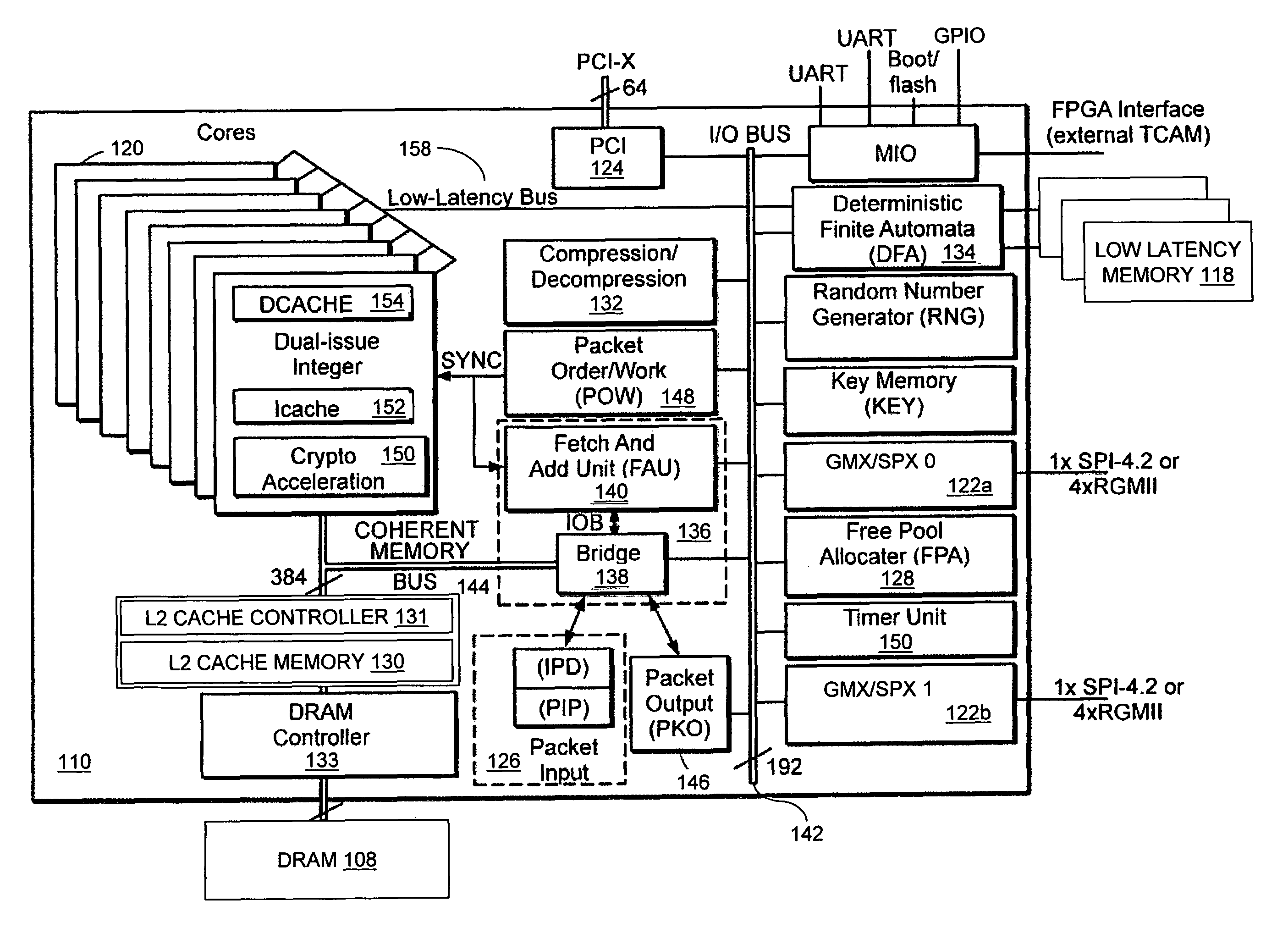
Deterministic finite automata (DFA) processing
ActiveUS20060069872A1Increase speedDigital computer detailsMemory systemsAsynchronous operationParallel computing
Owner:MARVELL ASIA PTE LTD
Fast processing of an XML data stream
InactiveUS20080082484A1Digital data information retrievalSpecial data processing applicationsConjunctive querySemi-structured data
To answer one or more queries of semistructured data, an answer automaton is constructed, based at least in part on the queries and on a schema of the data. The answer automaton is applied to the data to answer the queries. Preferably, to construct the answer automaton, a schema automaton is constructed for the schema, a query automaton is constructed for the queries, and the schema automaton and the query automaton are merged. If there are more than one query, separate query automata are constructed for the different queries and then are united to provide a joint query automaton. Preferably, all the automata are deterministic finite automata. Most preferably, all the automata are isostate automata.
Owner:RAMOT AT TEL AVIV UNIV LTD
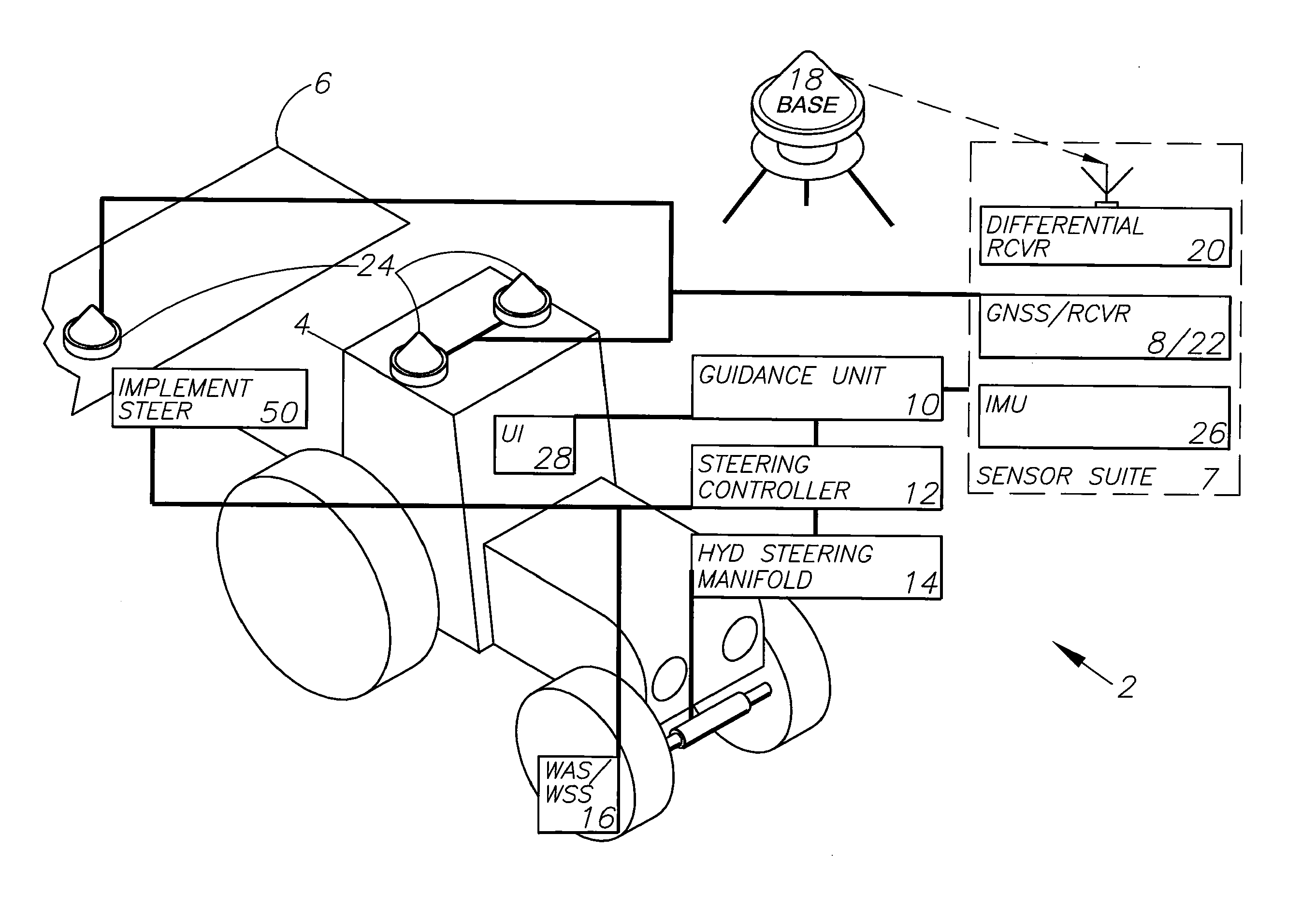
GNSS integrated multi-sensor control system and method
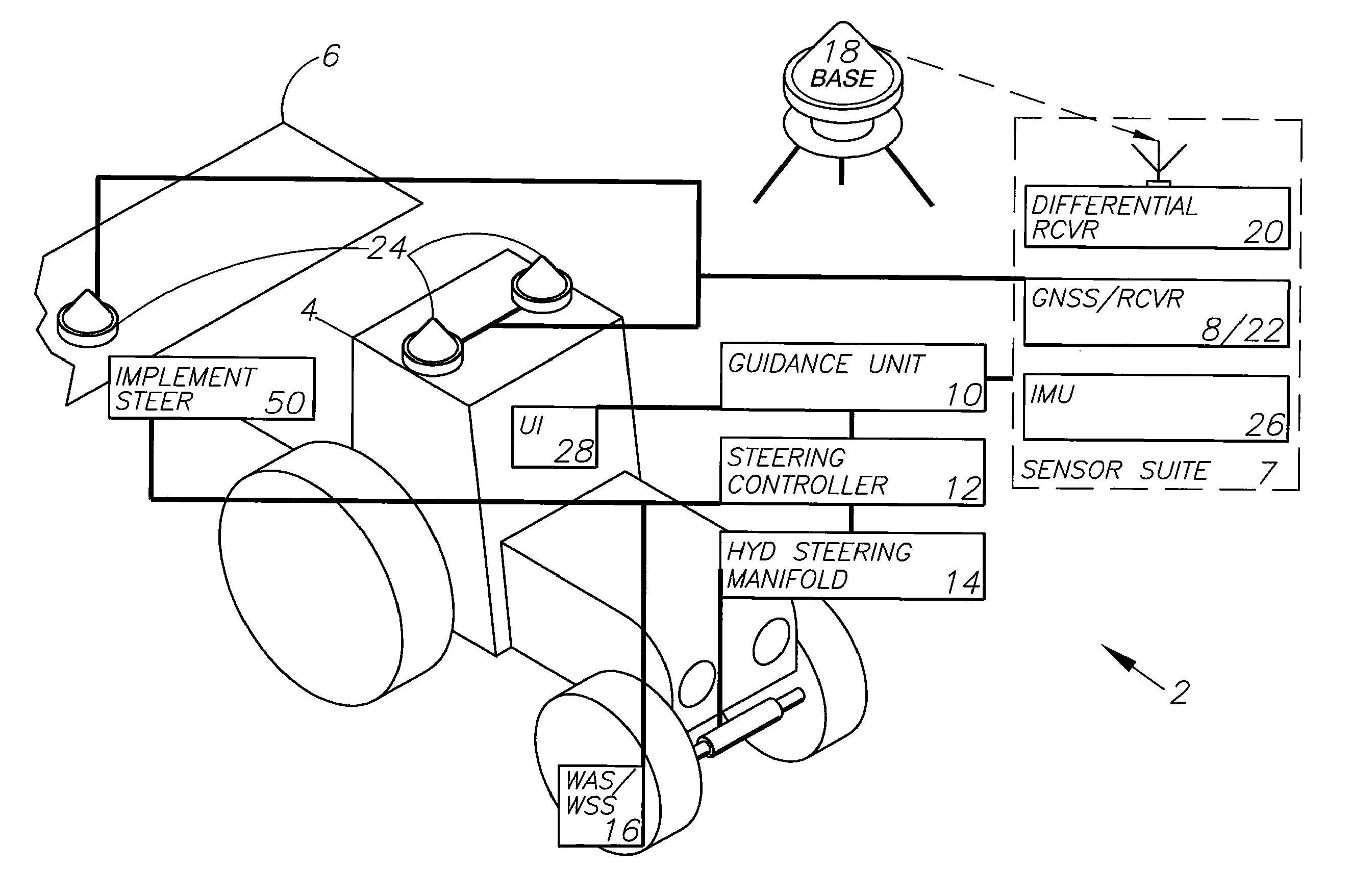
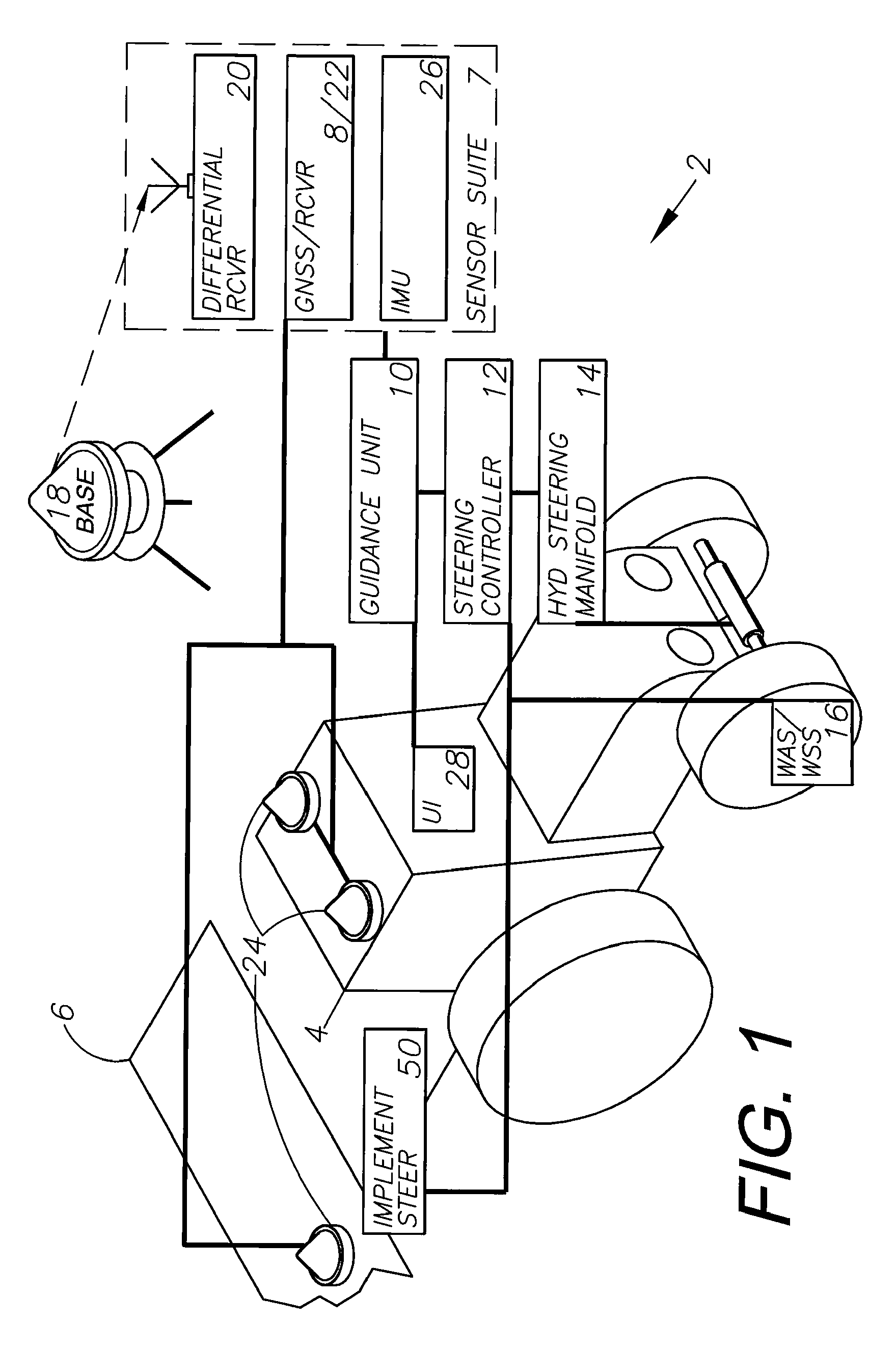
ActiveUS20110231061A1Accurate and precise vehicle positioning guidanceAccurate and precise and controlSteering initiationsDigital data processing detailsVehicle dynamicsGuidance system
A GNSS integrated multi-sensor guidance system for a vehicle assembly includes a suite of sensor units, including a global navigation satellite system (GNSS) sensor unit comprising a receiver and an antenna. An inertial measurement unit (IMU) outputs vehicle dynamic information for combining with the output of the GNSS unit. A controller with a processor receives the outputs of the sensor suite and computes steering solutions, which are utilized by vehicle actuators, including an automatic steering control unit connected to the vehicle steering for guiding the vehicle. The processor is programmed to define multiple behavior-based automatons comprising self-operating entities in the guidance system, which perform respective behaviors using data output from one or more sensor units for achieving the behaviors. A GNSS integrated multi-sensor vehicle guidance method is also disclosed.
Owner:AGJUNCTION
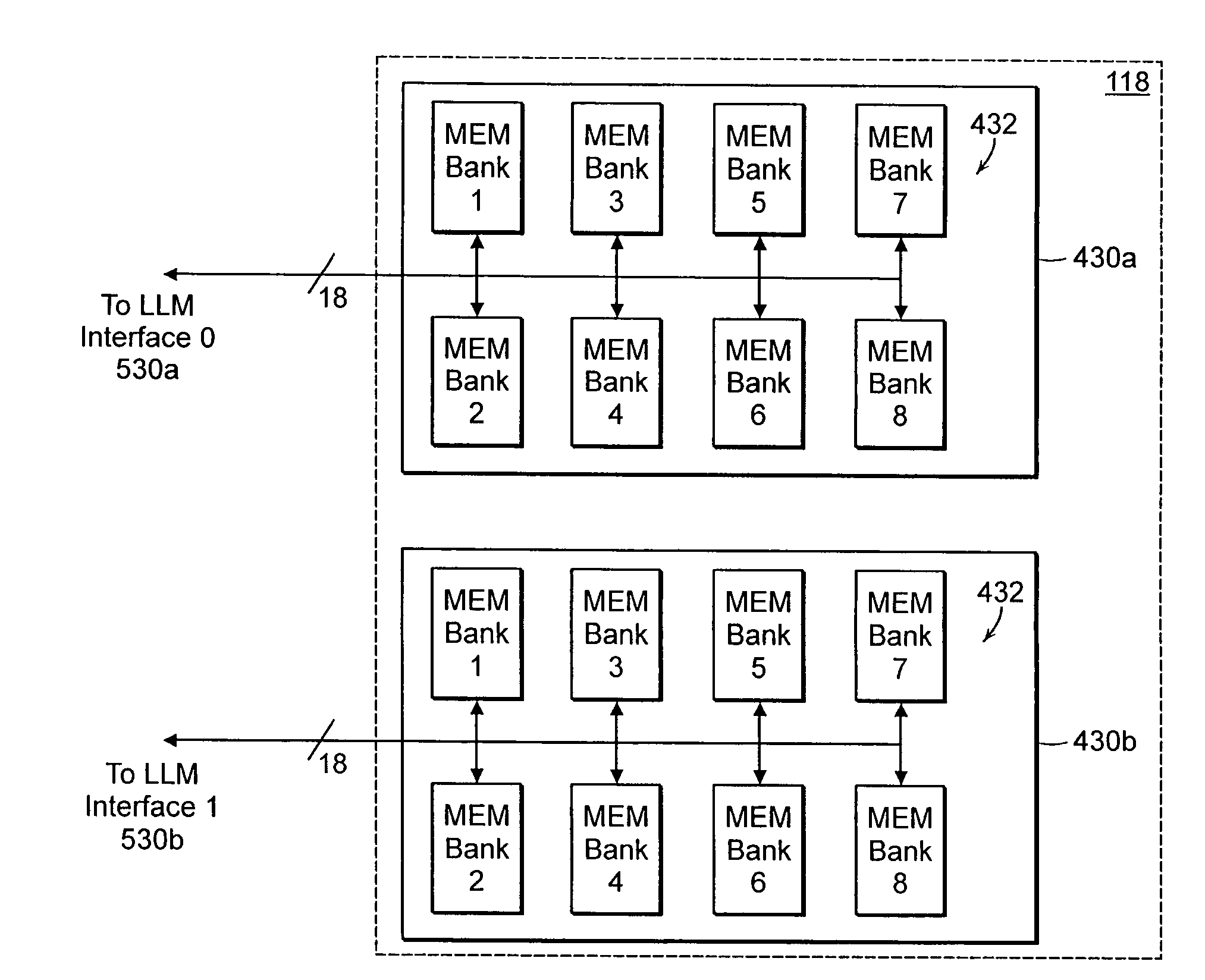
Selective replication of data structures
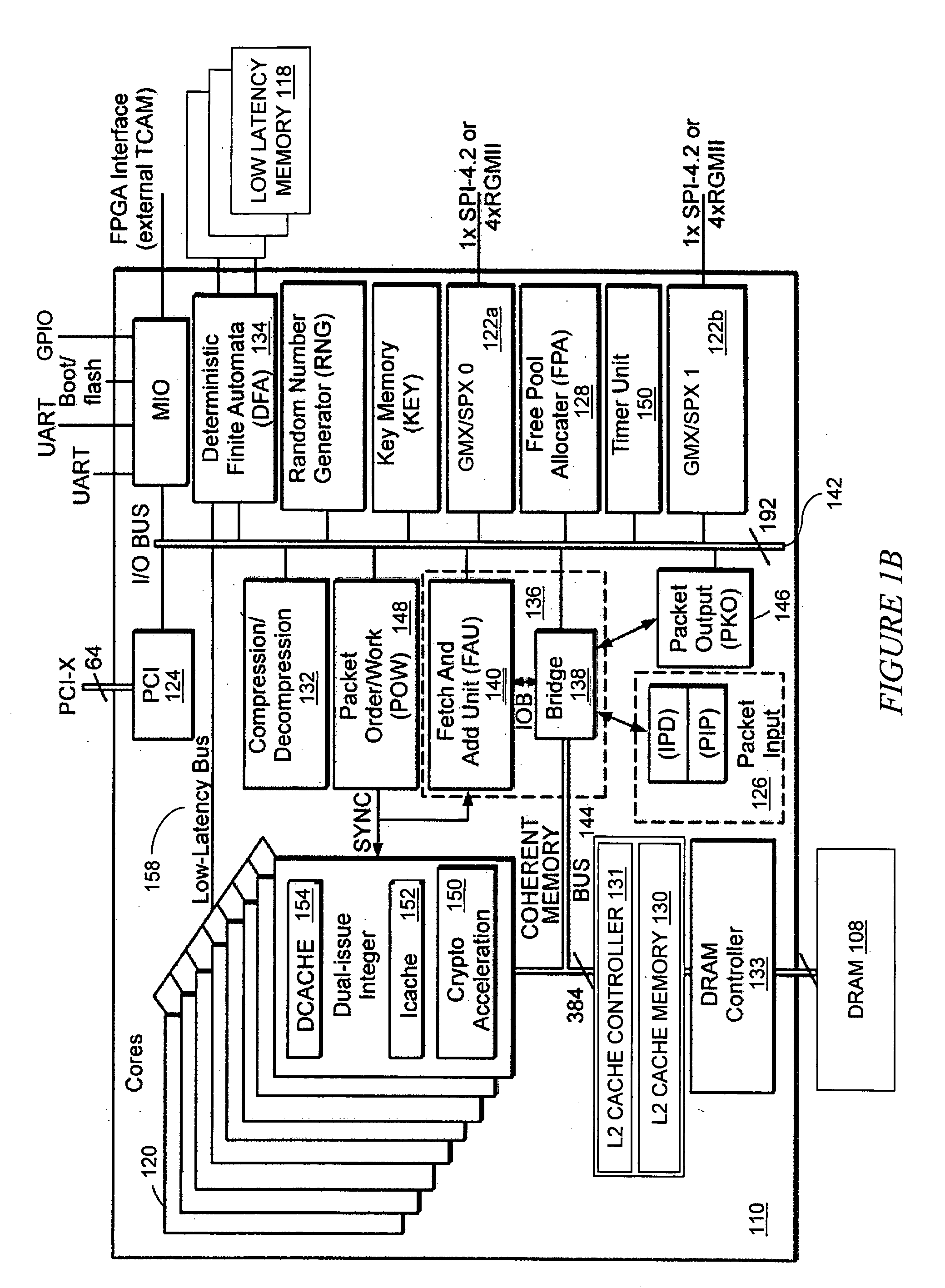
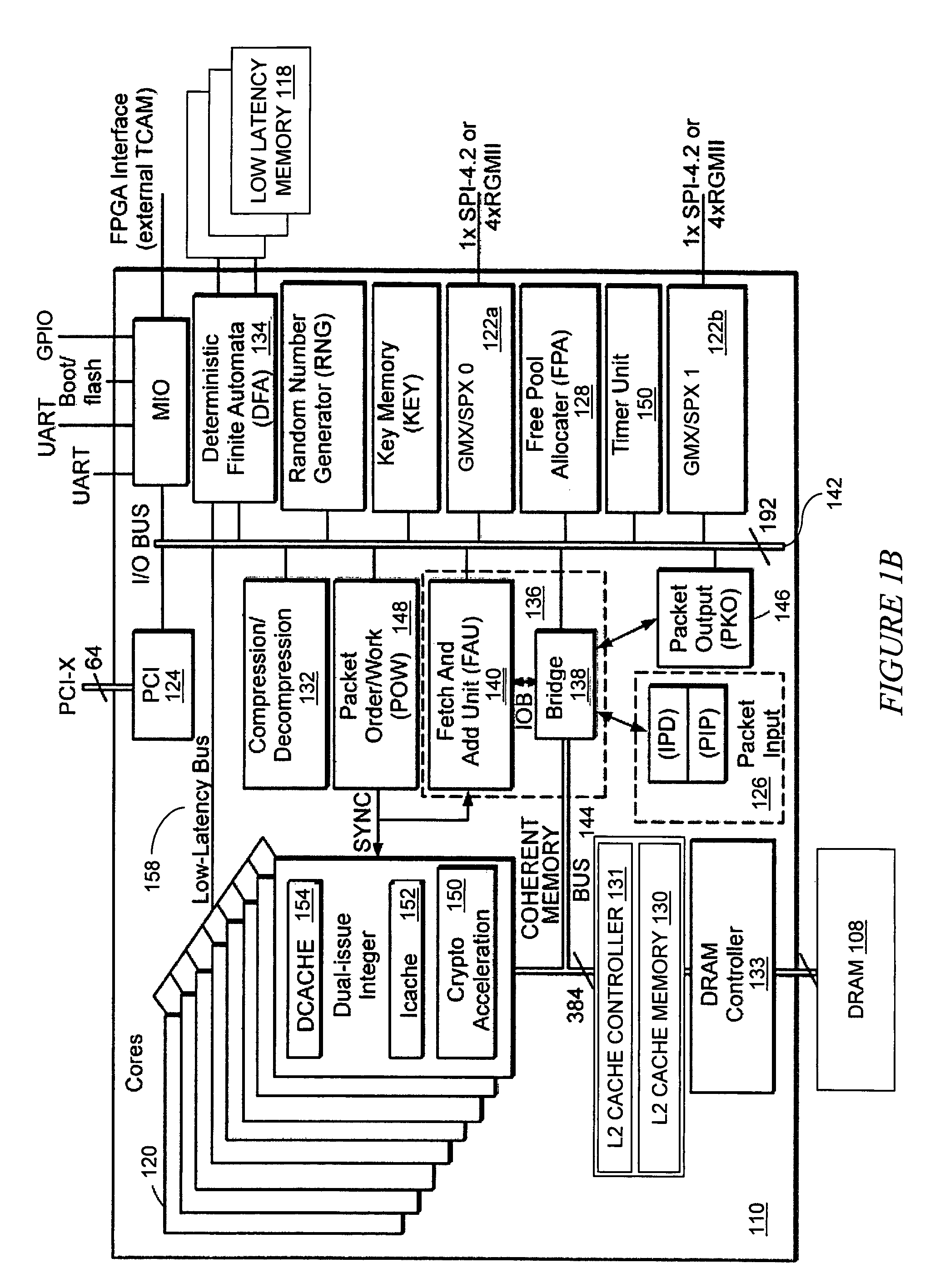
ActiveUS7558925B2Reduce delaysLow-latency memoryMemory architecture accessing/allocationMemory adressing/allocation/relocationArray data structureMemory bank
Methods and apparatus are provided for selectively replicating a data structure in a low-latency memory. The memory includes multiple individual memory banks configured to store replicated copies of the same data structure. Upon receiving a request to access the stored data structure, a low-latency memory access controller selects one of the memory banks, then accesses the stored data from the selected memory bank. Selection of a memory bank can be accomplished using a thermometer technique comparing the relative availability of the different memory banks. Exemplary data structures that benefit from the resulting efficiencies include deterministic finite automata (DFA) graphs and other data structures that are loaded (i.e., read) more often than they are stored (i.e., written).
Owner:MARVELL ASIA PTE LTD
Method for translating programs for reconfigurable architectures
InactiveUS7210129B2General purpose stored program computerSpecific program execution arrangementsHigh-level programming languageOperand
A method for translating high-level languages to reconfigurable architectures is disclosed. The method includes building a finite automaton for calculation. The method further includes forming a combinational network of a plurality of individual functions in accordance with the structure of the finite automaton. The method further includes allocating a plurality of memories to the network for storing a plurality of operands and a plurality of results.
Owner:PACT INFORMATIONSTECH +1
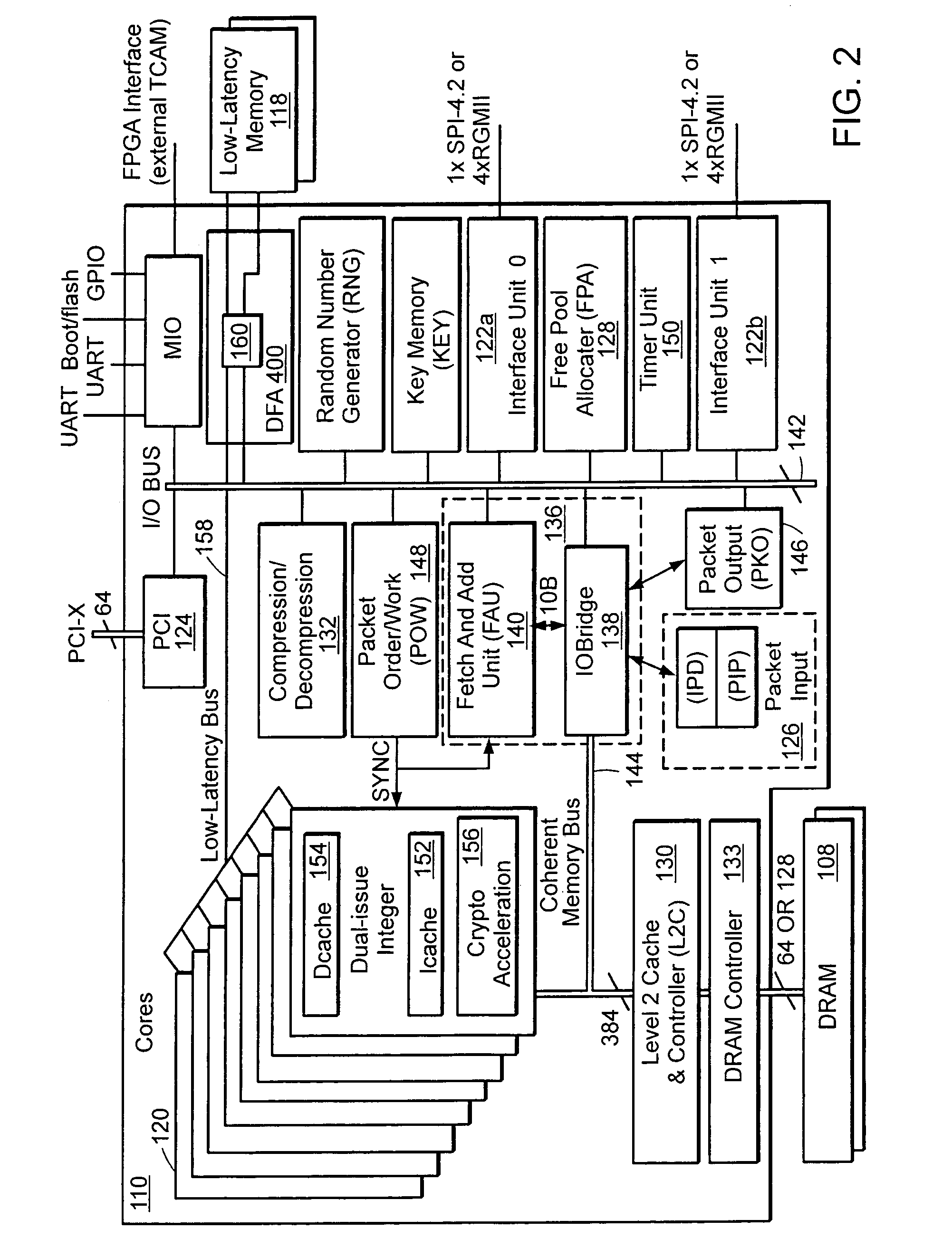
Embedded Programmable Intelligent Search Memory
ActiveUS20080140661A1Reduce classification overheadImprove performanceDigital data information retrievalDigital data processing detailsMulti processorMemory architecture
Memory architecture provides capabilities for high performance content search. The architecture creates an innovative memory that can be programmed with content search rules which are used by the memory to evaluate presented content for matching with the programmed rules. When the content being searched matches any of the rules programmed in the Programmable intelligent Search Memory (PRISM) action(s) associated with the matched rule(s) are taken The PRISM content search memory is embedded in a single core or multi-core processors or in multi-processor systems to perform content search. PRISM accelerates content search by offloading the content search tasks from the processors. Content search rules comprise of regular expressions which are converted to finite state automata and then programmed in PRISM for evaluating content with the search rules.
Owner:INFOSIL INC
GNSS integrated multi-sensor control system and method
ActiveUS8649930B2Facilitate numberSteering initiationsDigital data processing detailsVehicle dynamicsGuidance system
A GNSS integrated multi-sensor guidance system for a vehicle assembly includes a suite of sensor units, including a global navigation satellite system (GNSS) sensor unit comprising a receiver and an antenna. An inertial measurement unit (IMU) outputs vehicle dynamic information for combining with the output of the GNSS unit. A controller with a processor receives the outputs of the sensor suite and computes steering solutions, which are utilized by vehicle actuators, including an automatic steering control unit connected to the vehicle steering for guiding the vehicle. The processor is programmed to define multiple behavior-based automatons comprising self-operating entities in the guidance system, which perform respective behaviors using data output from one or more sensor units for achieving the behaviors. A GNSS integrated multi-sensor vehicle guidance method is also disclosed.
Owner:AGJUNCTION
Apparatus and method for automatic airborne LiDAR data processing and mapping using data obtained thereby
Apparatus for processing of a LiDAR point cloud of a ground scan, comprises: a point cloud input for receiving said LiDAR point cloud, a ground filter for filtering out points that belong to the ground from said point cloud, thereby to generate an elevation map showing features extending from the ground, an automatic feature search and recognition unit associated with said three dimensional graphical engine for searching said elevation map of said three-dimensional model to identify features therein and to replace points associated with said feature with a virtual object representing said feature, thereby to provide objects within said data; and a three-dimensional graphical renderer supporting three-dimensional graphics, to generate a three-dimensional rendering of said ground scan.
Owner:TILTAN SYST ENG
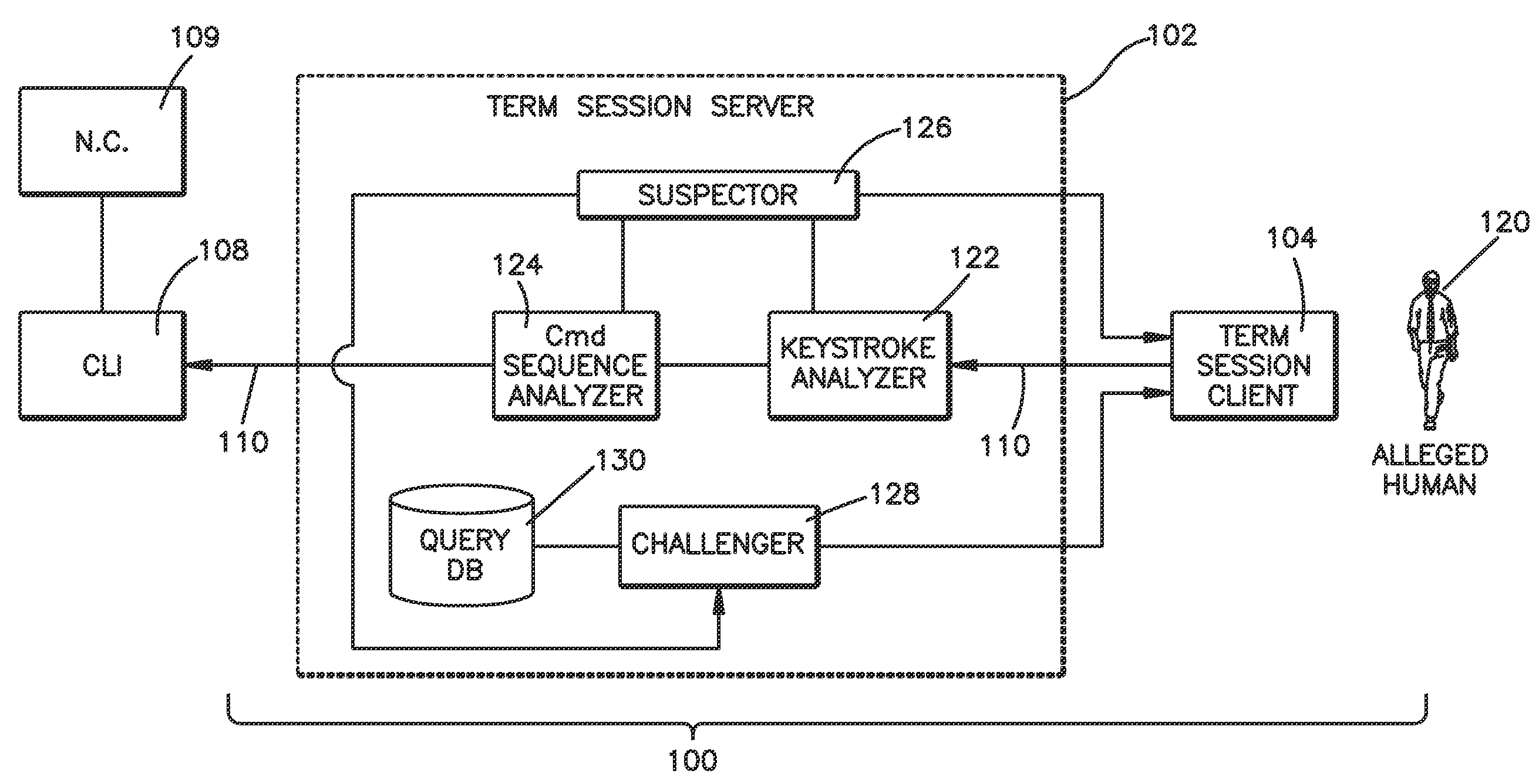
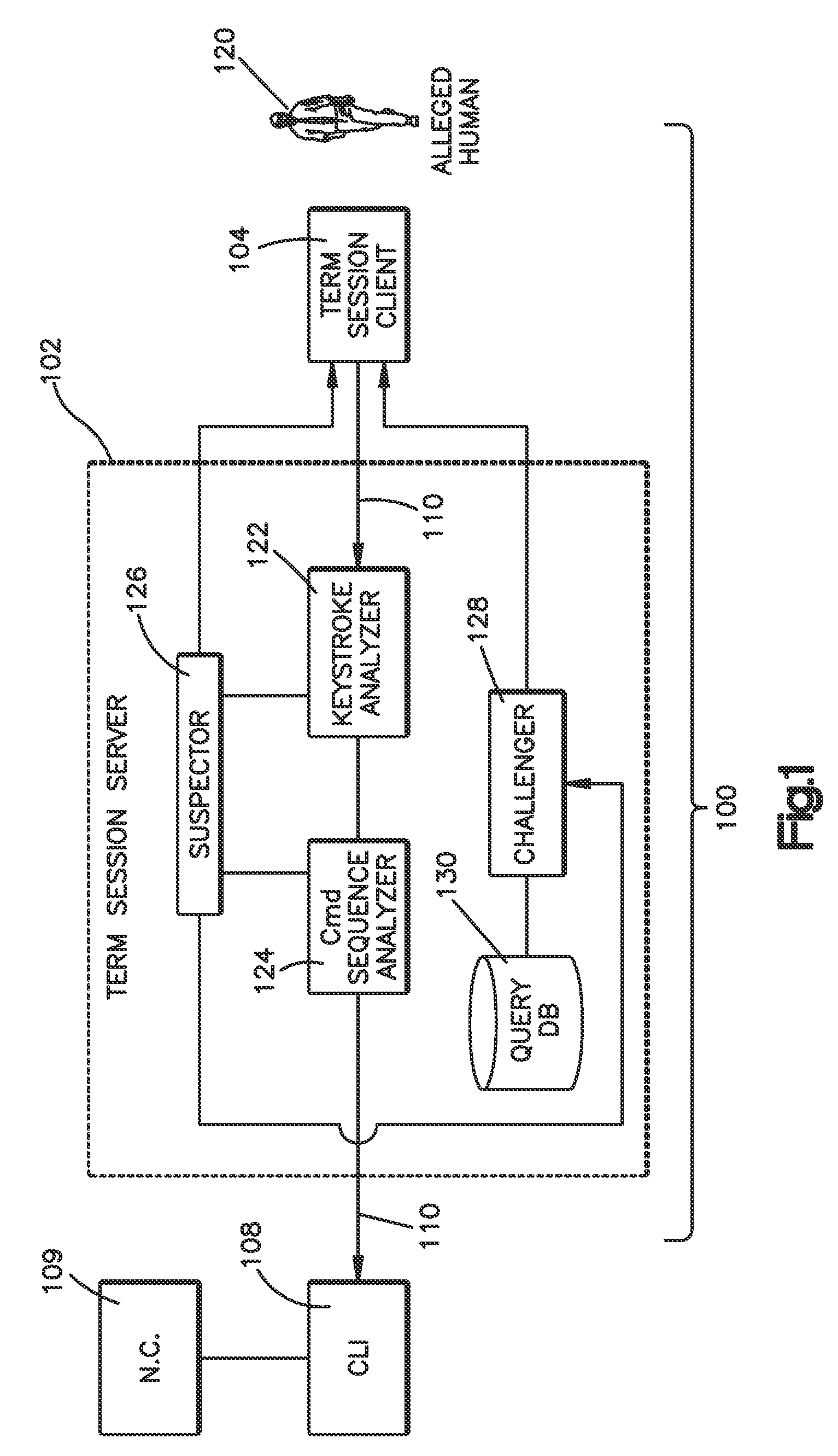
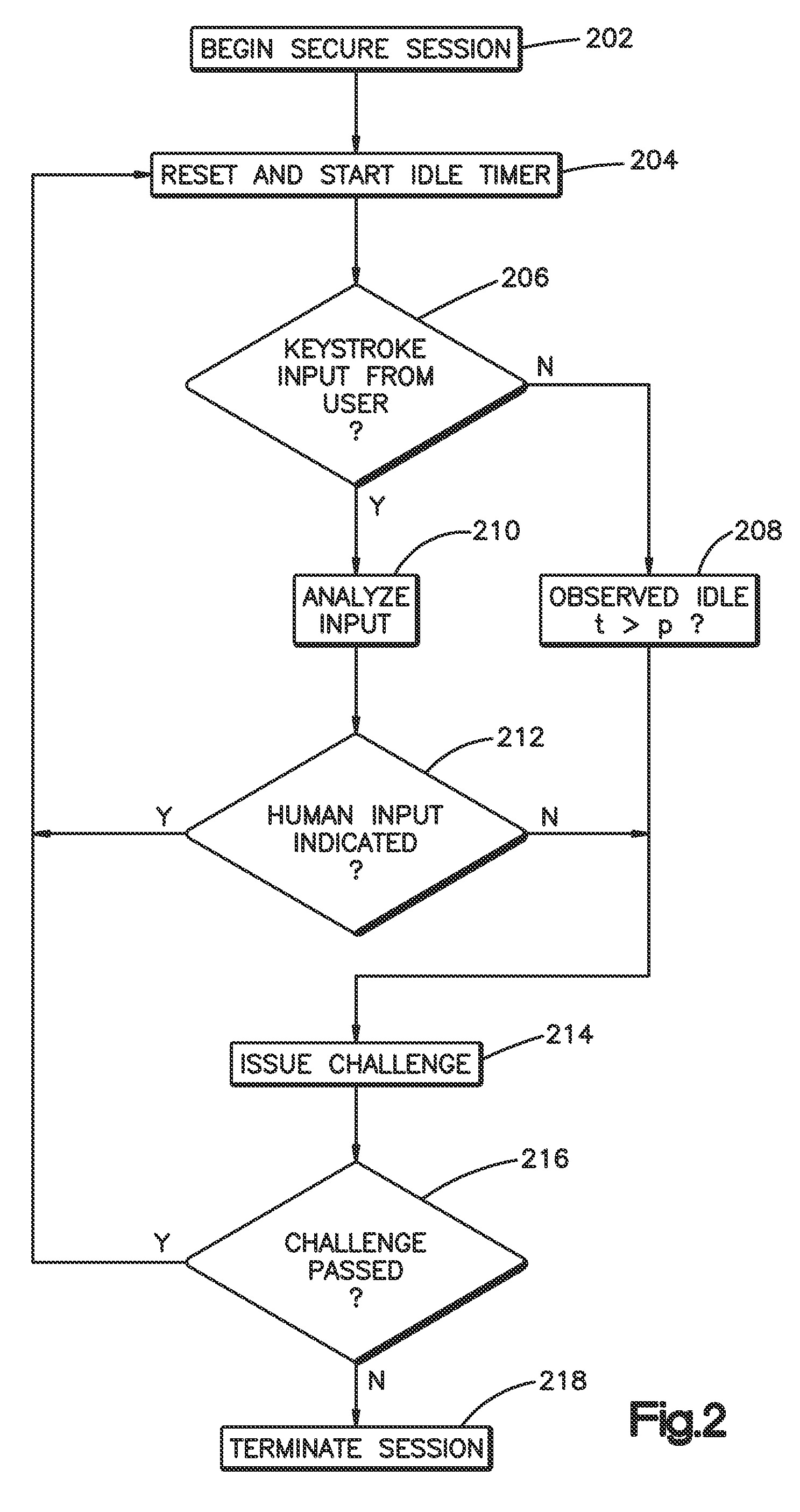
Method and system for validating active computer terminal sessions
InactiveUS20080263636A1Memory loss protectionDigital data processing detailsSequence analysisCommand-line interface
Systems, methods and program codes are provided wherein an analyzer analyzes input from a terminal device; ascertains human-like behavior; and terminates an active session, generates a time-out warning, manipulates an idle session timer or presents a challenge in response to a humanness likelihood determination or to a challenge result. In one aspect a keystroke analyzer and a command sequence analyzer determine whether the terminal device input is likely from a human user or from an automaton. In another aspect a Completely Automated Public Turing Test to tell Computers and Humans Apart challenge is presented. Timing characteristics include maximum generation rate, burstiness, and keystroke sequence delays, and command characteristics include a no-action-required characteristic and a query characteristic. A command sequence analyzer may have an affinity for a command line interface. Weighting algorithms or artificial intelligence routines may be applied to humanness likelihood outputs.
Owner:IBM CORP
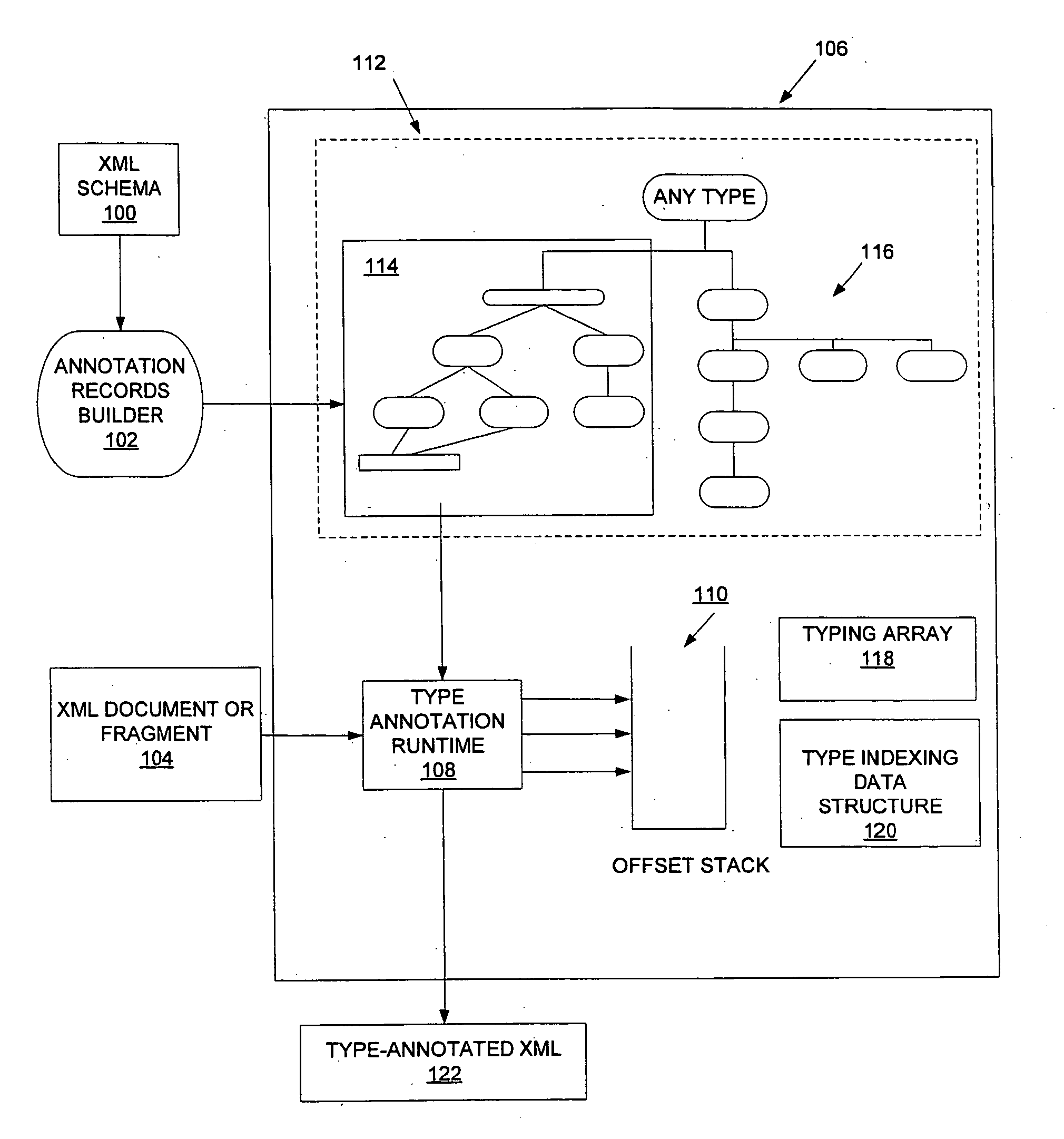
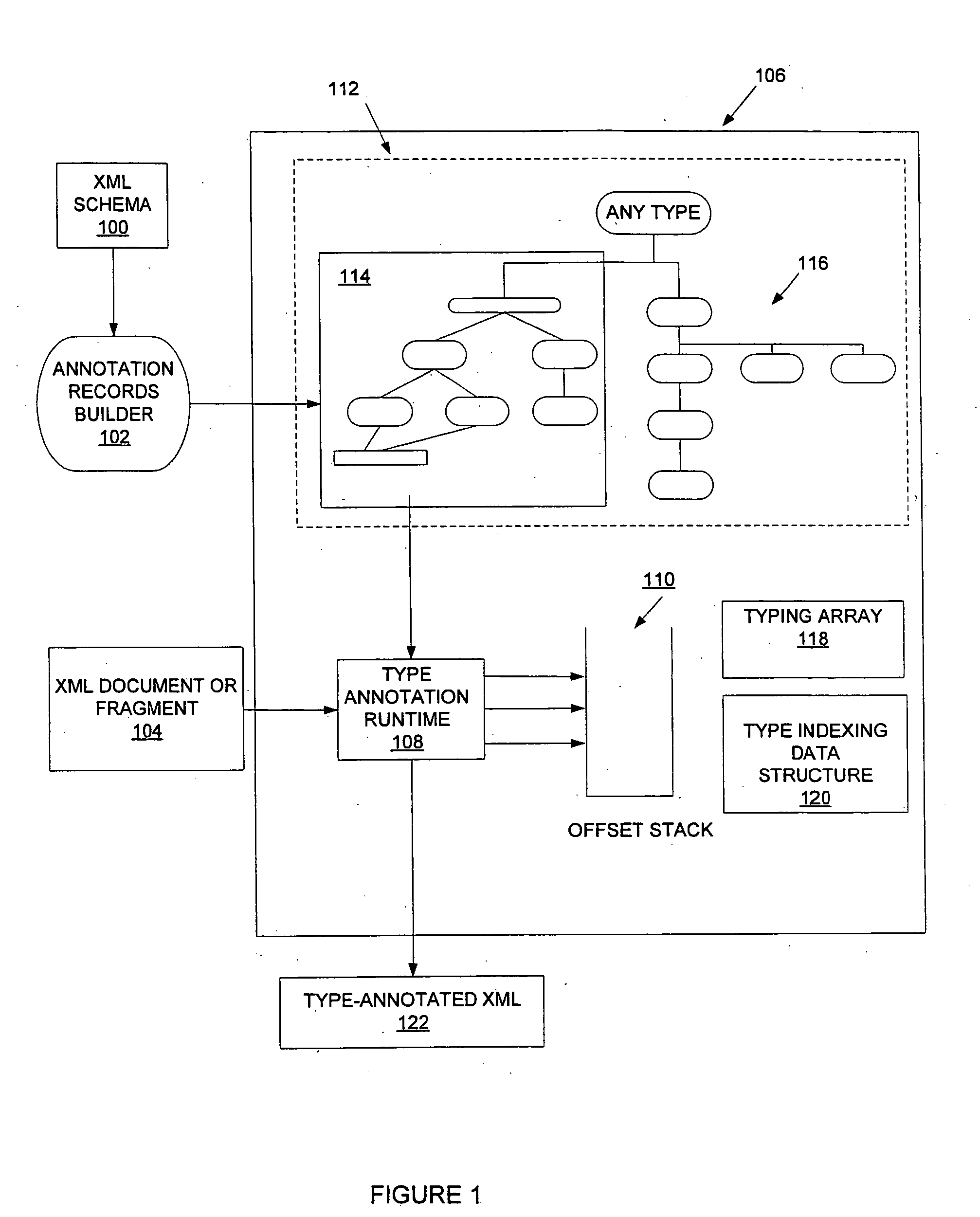
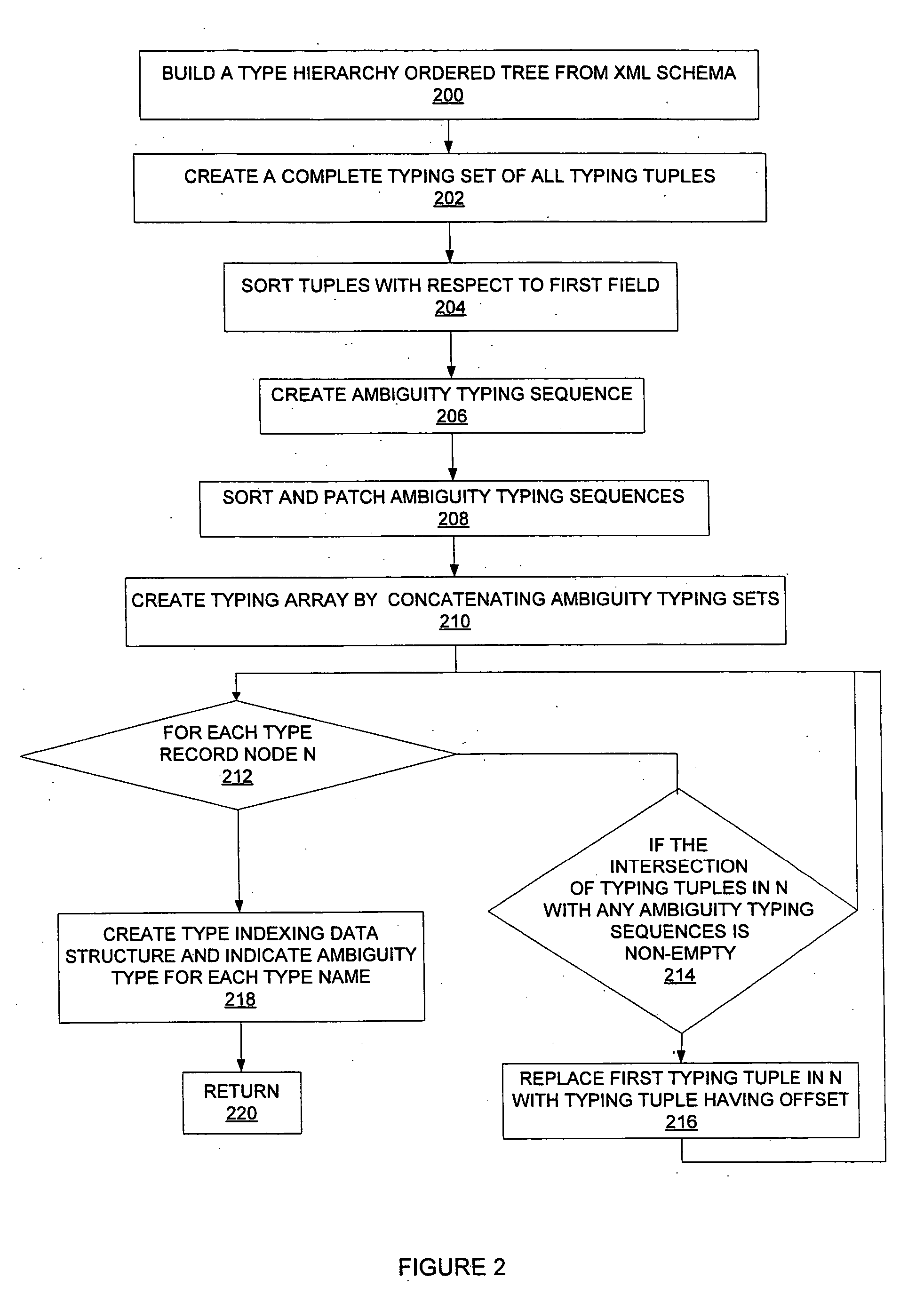
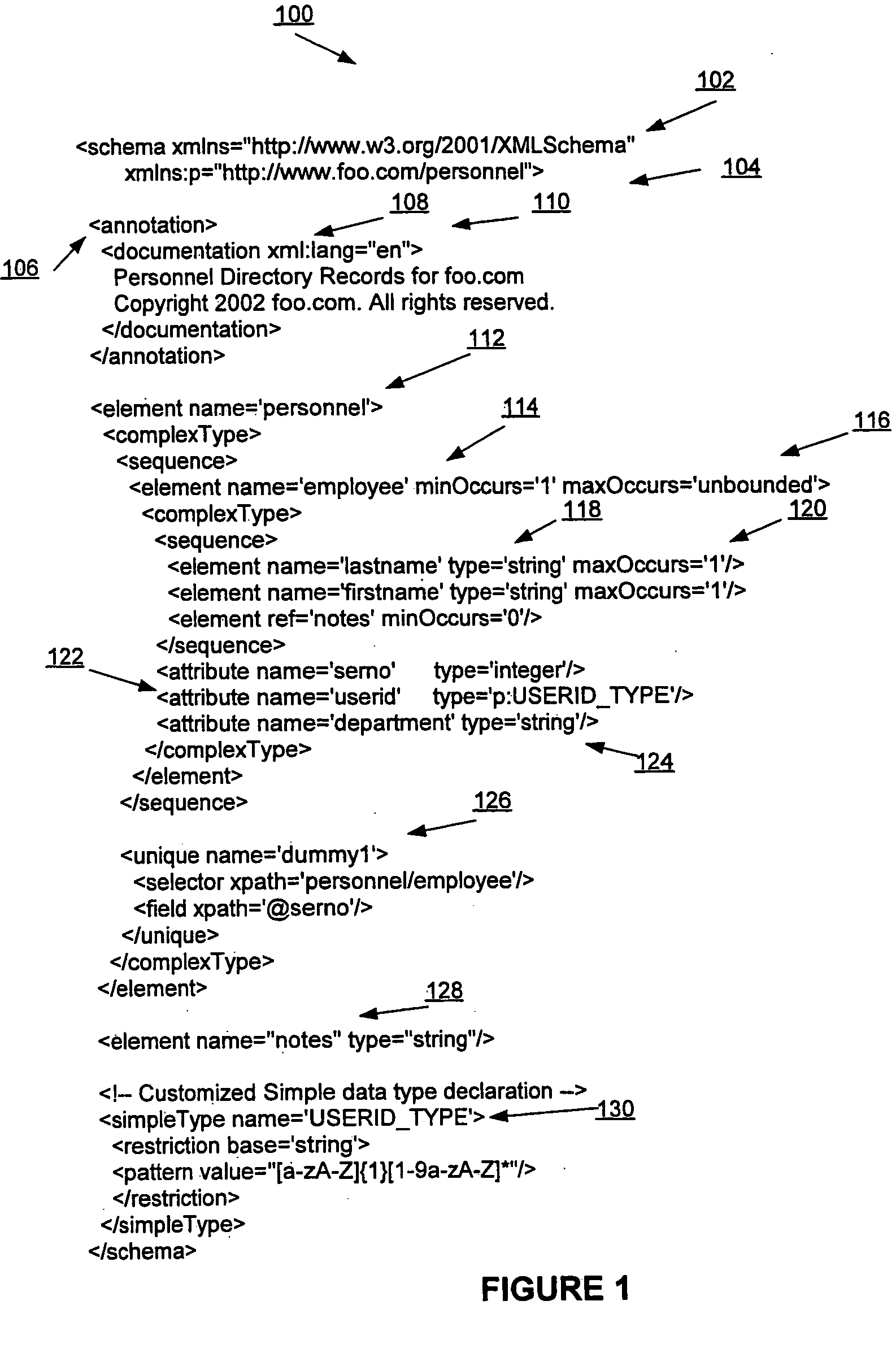
Efficient type annontation of XML schema-validated XML documents without schema validation
InactiveUS20050177578A1Efficiently annotate either entire XML document and XMLDigital data processing detailsSemi-structured data indexingXML schemaPaper document
Type annotation record information storage for annotated automaton encoding for high-performance XML schema validation is optimized in a space efficient aspect. Subsequent to type annotation record information organization, type annotation records are used for type annotation of validated XML documents, either by implementing annotation records and type annotation part of an algorithm only, or by skipping one or more validation steps in a full validation implementation. Given a schema context, a type annotation may be performed for a validated XML fragment as opposed to an entire document. In addition, default features such as attribute and type are supported.
Owner:IBM CORP
FSA Context Switch Architecture for Programmable Intelligent Search Memory
ActiveUS20090049230A1Reduce overheadSoap detergents with organic compounding agentsDigital data information retrievalMemory architectureAutomaton
Memory architecture provides capabilities for high performance content search. The architecture creates an innovative memory that can be programmed with content search rules which are used by the memory to evaluate presented content for matching with the programmed rules. When the content being searched matches any of the rules programmed in the Programmable Intelligent Search Memory (PRISM) action(s) associated with the matched rule(s) are taken. Content search rules comprise of regular expressions which are converted to finite state automata (FSA) and then programmed in PRISM for evaluating content with the search rules. PRISM architecture comprises of a plurality of programmable PRISM Search Engines (PSE) organized in PRISM memory clusters that are used simultaneously to search content presented to PRISM. A context switching architecture enables transitioning of PSE states between different input contexts.
Owner:INFOSIL INC
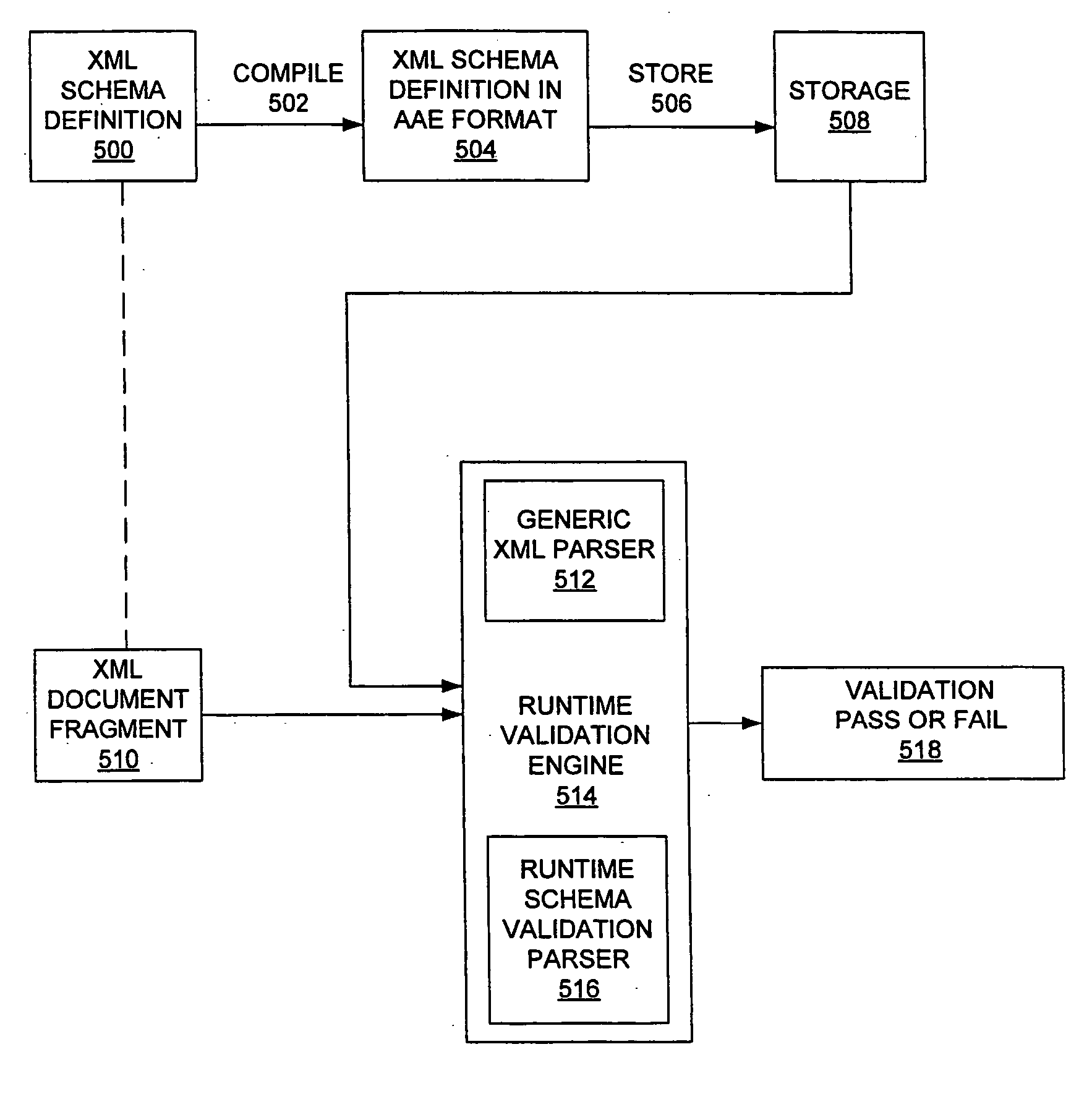
Efficient XML schema validation of XML fragments using annotated automaton encoding
InactiveUS20050177543A1Without compromising performanceSave a lot of timeDigital data processing detailsNatural language data processingXML schemaRuntime verification
A method and system for Extensible Markup Language (XML) schema validation, includes: loading an XML document into a runtime validation engine, where the runtime validation engine includes an XML schema validation parser; loading an annotated automaton encoding (AAE) for an XML schema definition into the XML schema validation parser; and validating the XML document against the XML schema definition by the XML schema validation parser utilizing the annotated automaton encoding. Each XML schema definition is compiled once into the AAE format, rather than being compiled each time an XML document is validated, and thus significant time is saved. The code for the runtime validation engine is fixed and does not vary depending on the XML schema definition, rather than varying for each XML schema definition, and thus space overhead is minimized. Flexibility in the validation process is provided without compromising performance.
Owner:IBM CORP
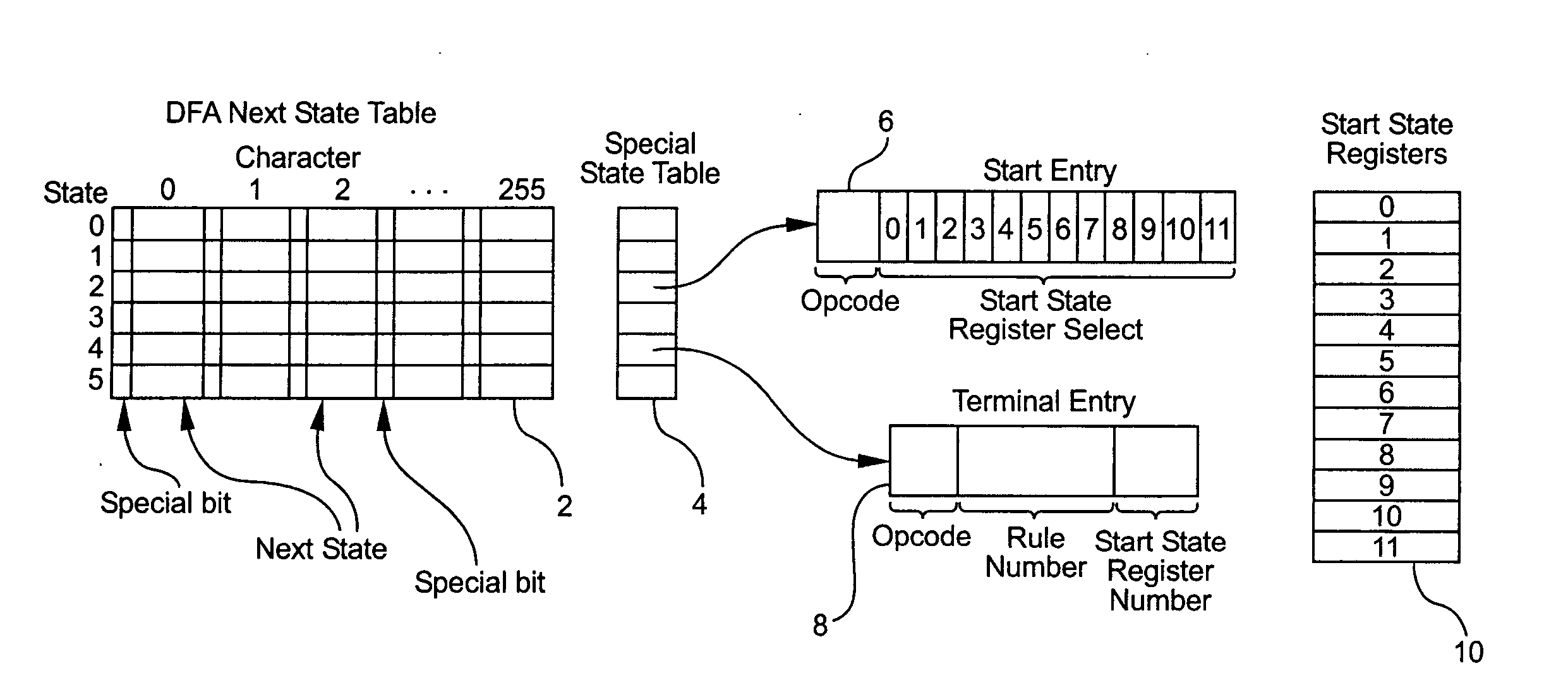
System and method for determining the start of a match of a regular expression
InactiveUS20080077587A1Overcome disadvantagesData processing applicationsDigital data information retrievalAutomatonRegular expression
A system for determining the start of a match of a regular expression has a special state table which contains start state entries and terminal state entries; a plurality of start state registers for storing offset information indicative of the start of a match of the regular expression; a deterministic finite state automaton (DFA) next state table which, given the current state and an input character, returns the next state. The DFA next state table includes a settable indicator for any next state table entry which indicates whether to perform a lookup into the special state table. A compiler loads values into the special state table based on the regular expression.
Owner:RAMBUS INC
Deterministic finite automata (DFA) processing
ActiveUS8392590B2Increase speedMultiple digital computer combinationsSpecial data processing applicationsAsynchronous operationParallel computing
Owner:MARVELL ASIA PTE LTD
Automata unit, a tool for designing checker circuitry and a method of manufacturing hardware circuitry incorporating checker circuitry
InactiveUS20080082946A1Computer aided designSoftware simulation/interpretation/emulationAutomatonDual layer
The present invention relates to an automata unit, a tool for designing circuitry and / or checker circuitry, and a method for manufacturing hardware circuitry. The automata unit includes an input unit for receiving assertions using Boolean expressions, an automata generator for translating the assertions into automata, and an automata adaptor. The automata generator uses a dual layer symbolic alphabet for representing the assertions, and the automata adaptor adapts automata algorithms so as to support the symbolic alphabet in the generated automata. The tools for designing circuitry and checker circuitry rely on the automata unit, and further include an assertion unit and either a circuit generator or a checker generator.
Owner:MCGILL UNIV
Compiler for Programmable Intelligent Search Memory
ActiveUS20080140600A1Efficient and compact realizationReduce overheadDigital data information retrievalDigital storageMemory architectureAutomaton
Memory architecture provides capabilities for high performance content search. Content search rules comprise of regular expressions which are compiled to finite state automata and then programmed in Programmable Intelligent Search Memory (PRISM) for evaluating content with the search rules. A compiler compiles the content search rules for evaluation by PRISM memory. The PRISM memory architecture creates an innovative memory that can be programmed with content search rules which are used by the memory to evaluate presented content for matching with the programmed rules. When the content being searched matches any of the rules programmed in the Programmable Intelligent Search Memory (PRISM) action(s) associated with the matched rule(s) are taken.
Owner:INFOSIL INC
Extended finite state automata and systems and methods for recognizing patterns using extended finite state automata
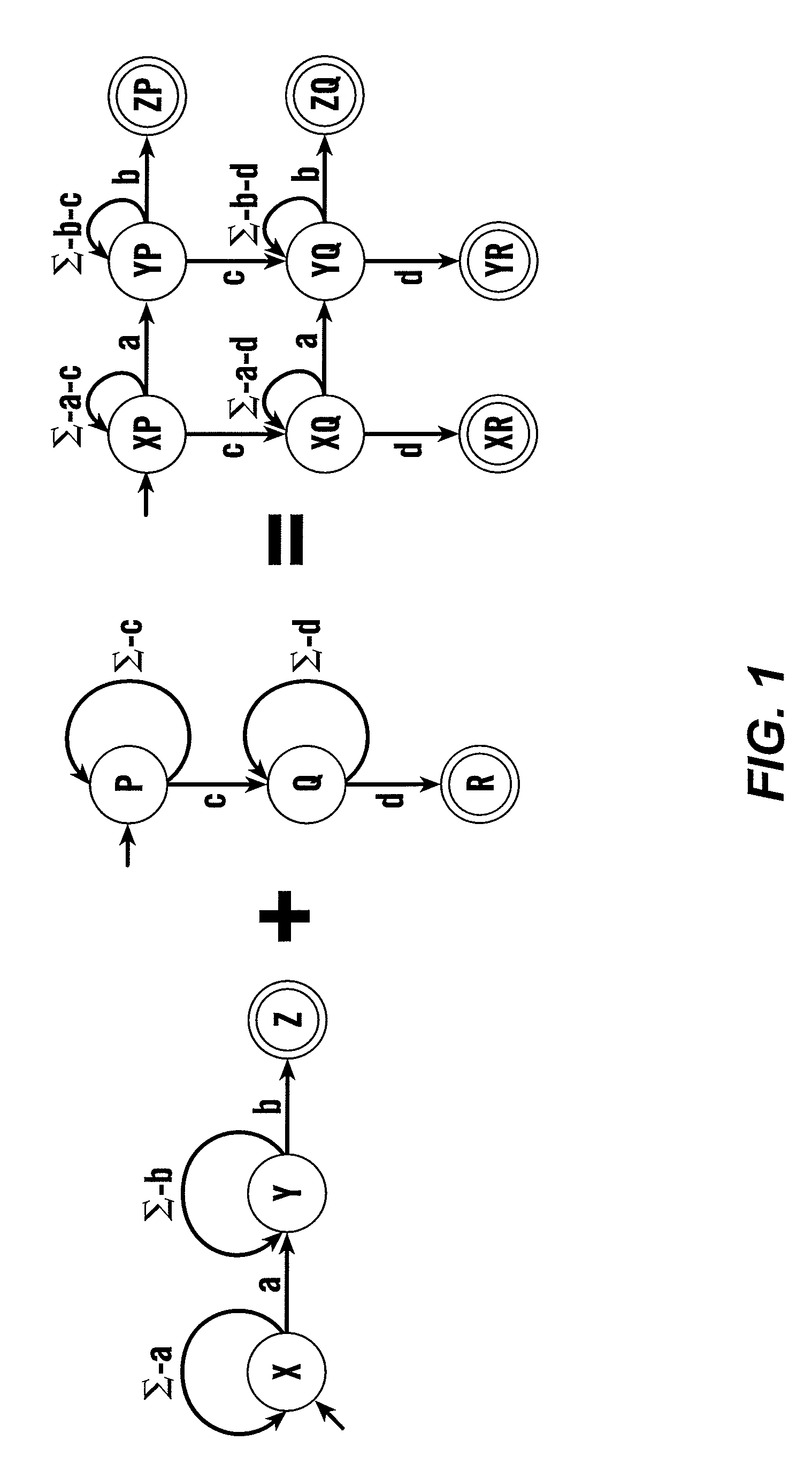
Deterministic finite automata (DFAs) are popular solutions to deep packet inspection because they are fast and DFAs corresponding to multiple signatures are combinable into a single DFA. Combining such DFAs causes an explosive increase in memory usage. Extended finite automata (XFAs) are an alternative to DFAs that avoids state-space explosion problems. XFAs extend DFAs with a few bytes of “scratch memory” used to store bits and other data structures that record progress. Simple programs associated with automaton states and / or transitions manipulate this scratch memory. XFAs are deterministic in their operation, are equivalent to DFAs in expressiveness, and require no custom hardware support. Fully functional prototype XFA implementations show that, for most signature sets, XFAs are at least 10,000 times smaller than the DFA matching all signatures. XFAs are 10 times smaller and 5 times faster or 5 times smaller and 20 times faster than systems using multiple DFAs.
Owner:WISCONSIN ALUMNI RES FOUND
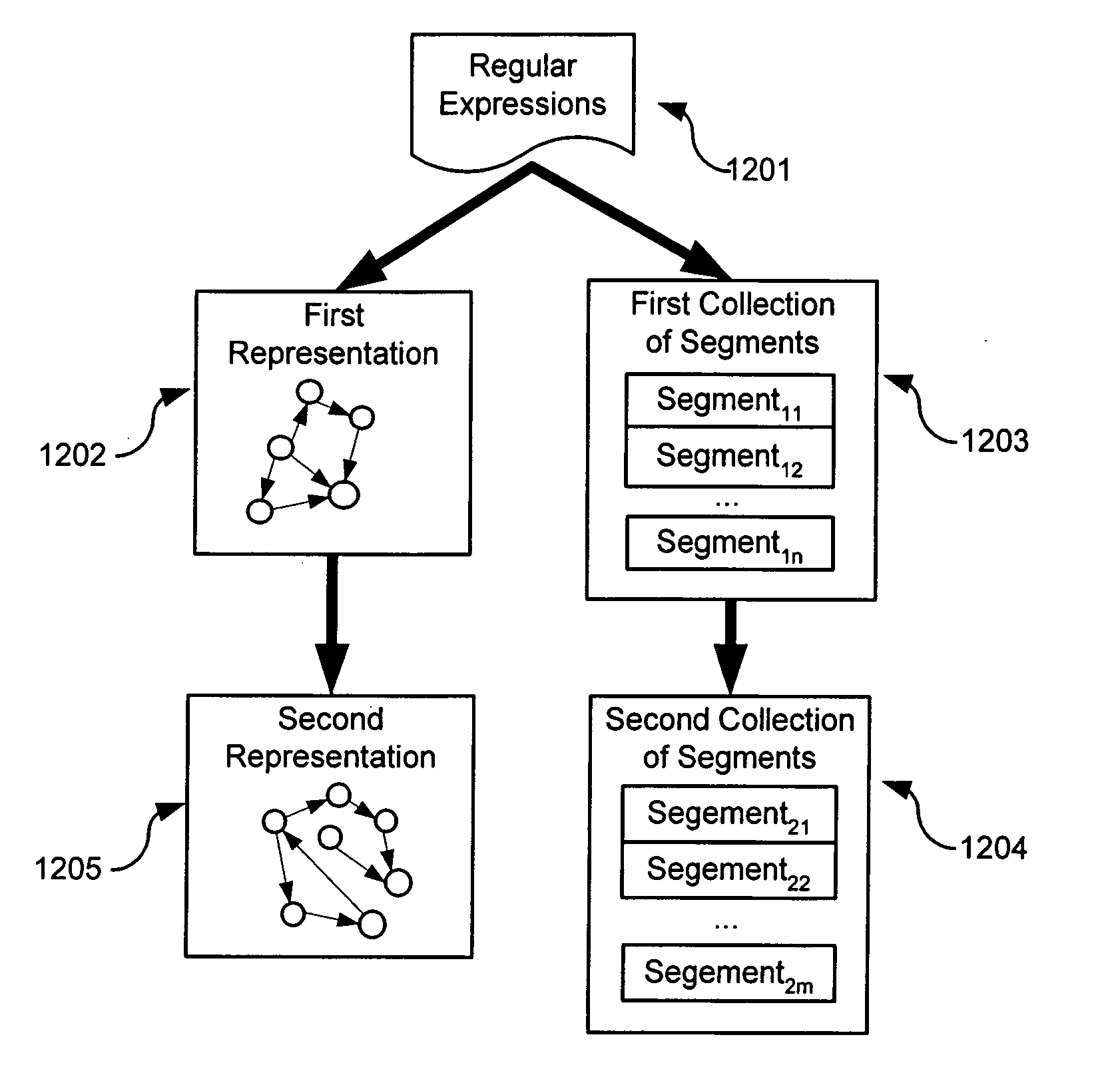
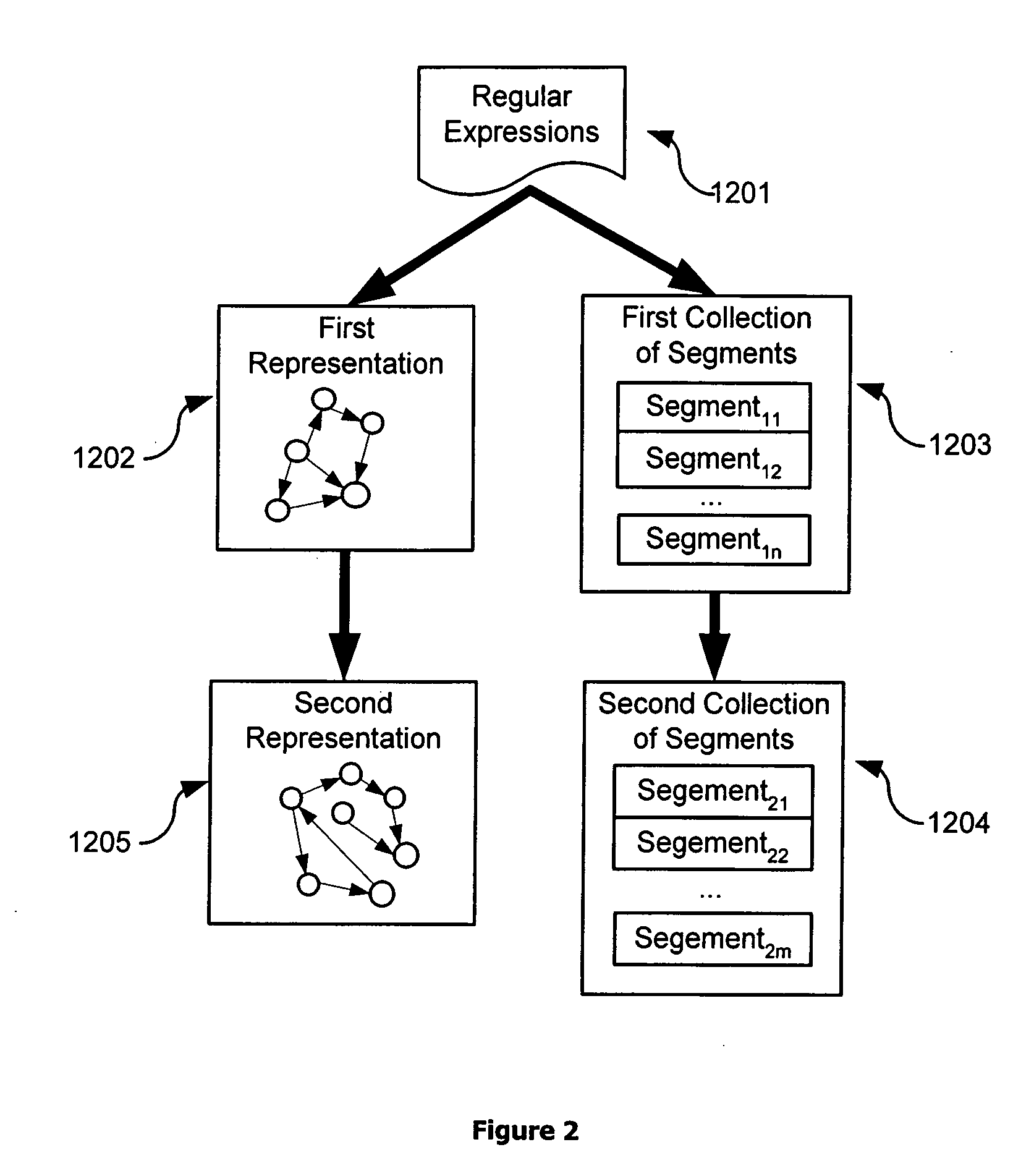
Method for transformation of regular expressions
InactiveUS20060085389A1Reduce memory requirementsDigital data information retrievalDigital data processing detailsSemanticsTerm memory
A method and apparatus for transforming regular expressions into a less resource intensive representation is disclosed. The method and apparatus converts a collection of regular expressions into a multi-level representation in which the memory requirements of the lowest level representation is reduced when compared with a conventional finite state automaton representation. The method and apparatus converts a collection of regular expressions into a collection of segments and a higher level representation in a way that retains the semantics of the original set of regular expressions. This transformation is performed through the use of an intermediate form. The resulting representation and collection admit an implementation which avoids the potentially costly memory requirements of a traditional implementation of the original expressions.
Owner:SENSORY NETWORKS +1
Method and system for multi-character multi-pattern pattern matching
ActiveUS7725510B2Increase speedEasy to implementData processing applicationsDigital data information retrievalPattern matchingTernary content addressable memory
Disclosed is a method and system for multi-character multi-pattern pattern matching. In the multi-character multi-pattern pattern matching method, patterns in an input stream are detected by transitioning between states of a “compressed deterministic finite state automaton (DFA)”, with each transition based on multiple characters of the input stream. The compressed DFA is created by compressing an original DFA, such as an Aho-Corasick DFA, such that each state of the compressed DFA represents multiple consecutive states of the original DFA and each transition between the states of the compressed DFA is a combination of all of the transitions between the multiple consecutive states of the original DFA. This method can be implemented using a Ternary Content-Addressable Memory (TCAM) to store the transitions of the compressed DFA and compares the transitions with multiple characters of an input stream at a time to detect patterns in the input stream.
Owner:ALGOGENE FINANCIAL TECHNOLOGY COMPANY LIMITED
FSA context switch architecture for programmable intelligent search memory
ActiveUS7890692B2Reduce overheadSoap detergents with organic compounding agentsDigital data information retrievalMemory architectureAutomaton
Memory architecture provides capabilities for high performance content search. The architecture creates an innovative memory that can be programmed with content search rules which are used by the memory to evaluate presented content for matching with the programmed rules. When the content being searched matches any of the rules programmed in the Programmable Intelligent Search Memory (PRISM) action(s) associated with the matched rule(s) are taken. Content search rules comprise of regular expressions which are converted to finite state automata (FSA) and then programmed in PRISM for evaluating content with the search rules. PRISM architecture comprises of a plurality of programmable PRISM Search Engines (PSE) organized in PRISM memory clusters that are used simultaneously to search content presented to PRISM. A context switching architecture enables transitioning of PSE states between different input contexts.
Owner:INFOSIL INC
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com