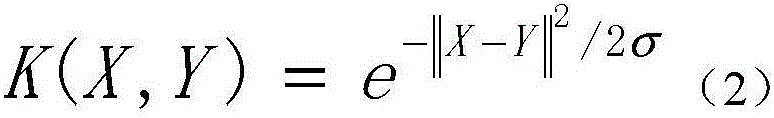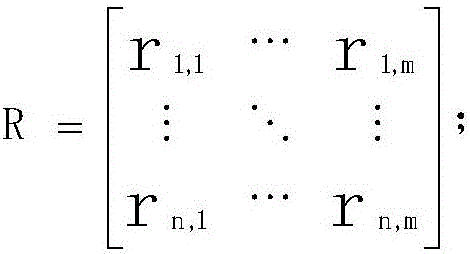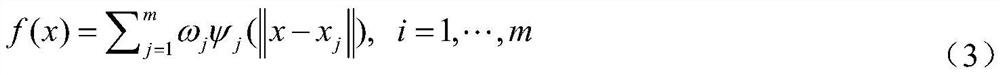Patents
Literature
Hiro is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
41 results about "Gaussian radial basis function" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
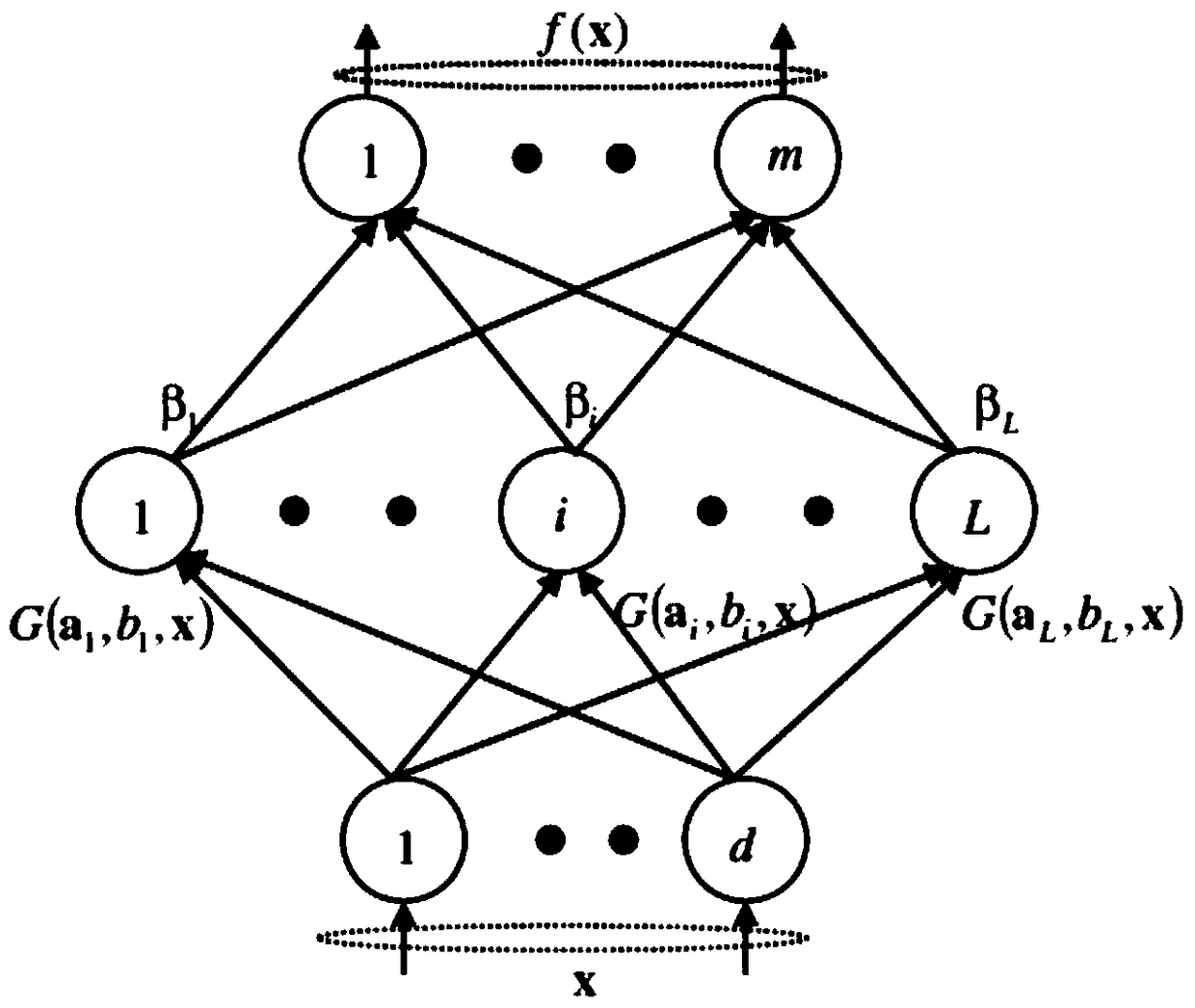
A radial basis function is a scalar function that depends on the distance to some point, called the center point, c. One popular radial basis function is the Gaussian kernel φ(x; c) = exp(-||x – c|| 2 / (2 σ 2)), which uses the squared distance from a vector x to the center c to assign a weight.
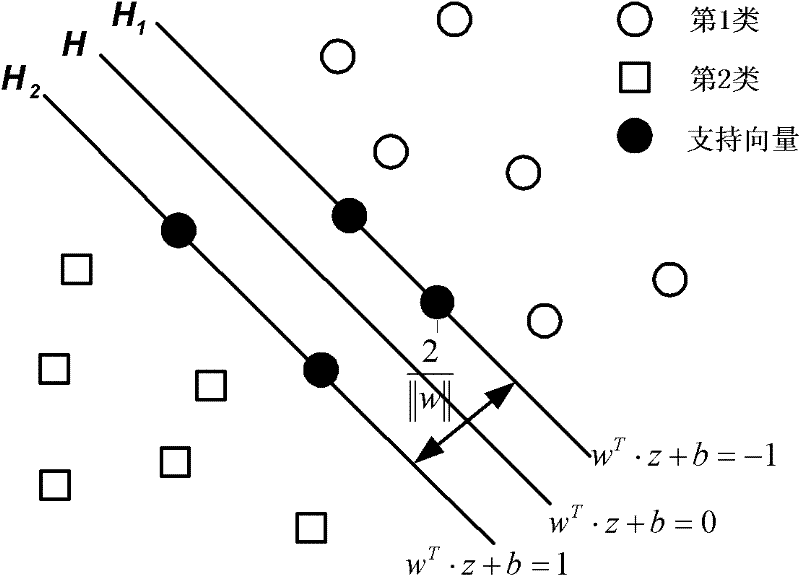
Rock-burst acoustic emission predicting method based on support vector machine (SVM)
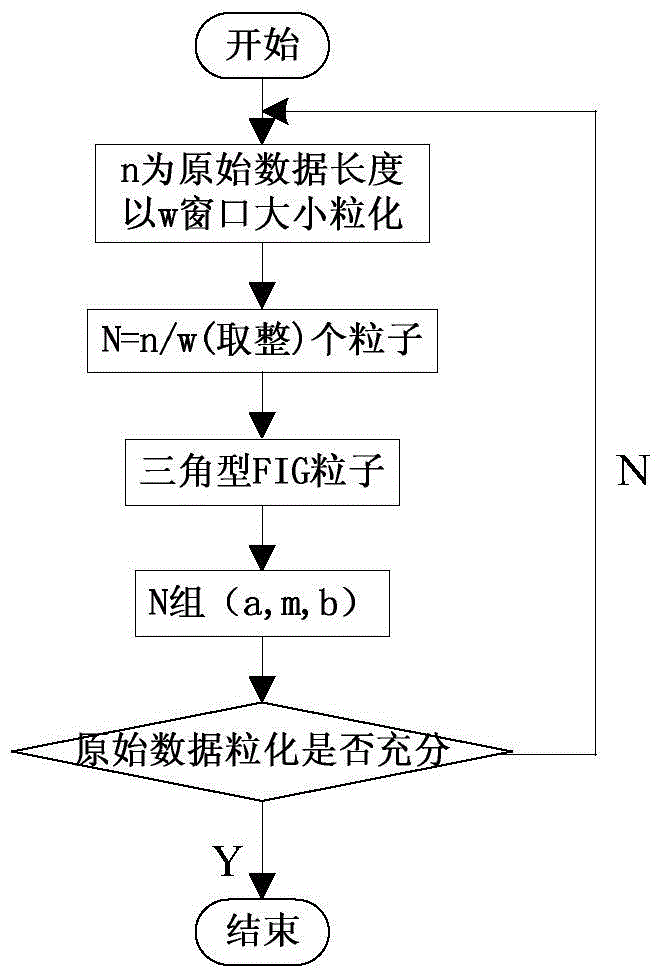
The invention belongs to the field of mining safety and relates to a rock-burst acoustic emission predicting method based on a support vector machine (SVM). The rock-burst acoustic emission predicting method includes using SVM regression prediction as a means, selecting energy release value as judgment indicator for predicting rock burst on the basis of test research analysis, using burst tendency physical and mechanic parameters and acoustic emission signal feature parameters as influence factor of rock burst, and generating SVM input vector by extracting sample data according to these parameters; selecting Gauss radial basis function (RBF) as kernel function of the SVM in setup of a SVM prediction model, and using the K-CV cross validation algorithm to optimize and select the optimal penalty parameter C and kernel function parameter g; applying a fuzzy information granulating data processing method into the regression prediction of the SVM so as to predict change trends and change space of the predicted values of the rock burst.
Owner:CHONGQING UNIV
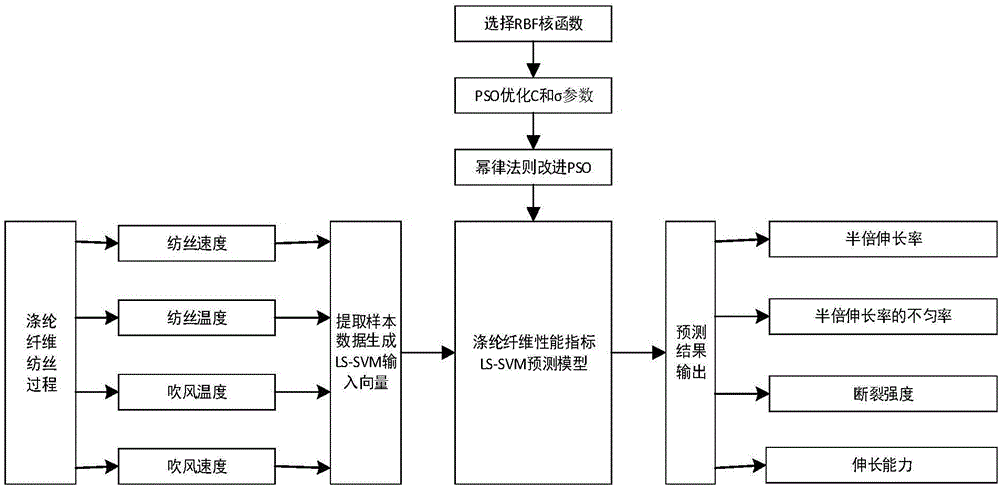
Method for predicting performance indexes in polyester fiber spinning process
InactiveCN106446315AEasy to filterEasy to replaceMulti-objective optimisationSpecial data processing applicationsPolyesterData set
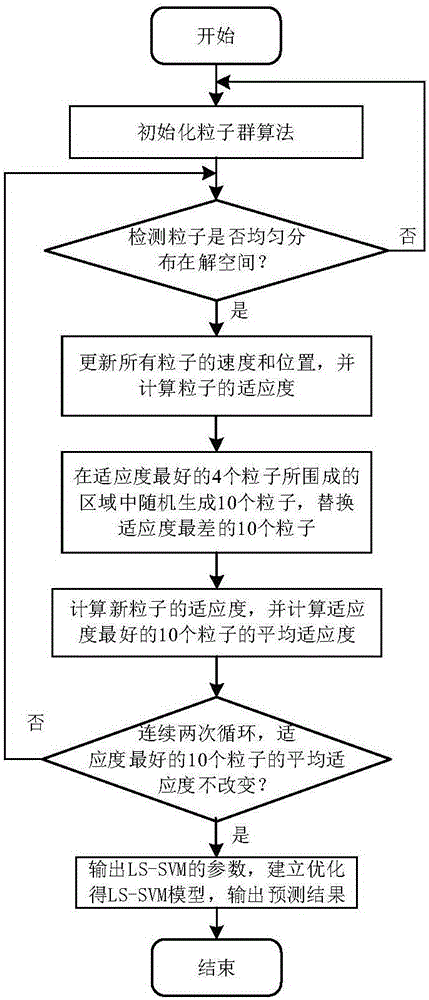
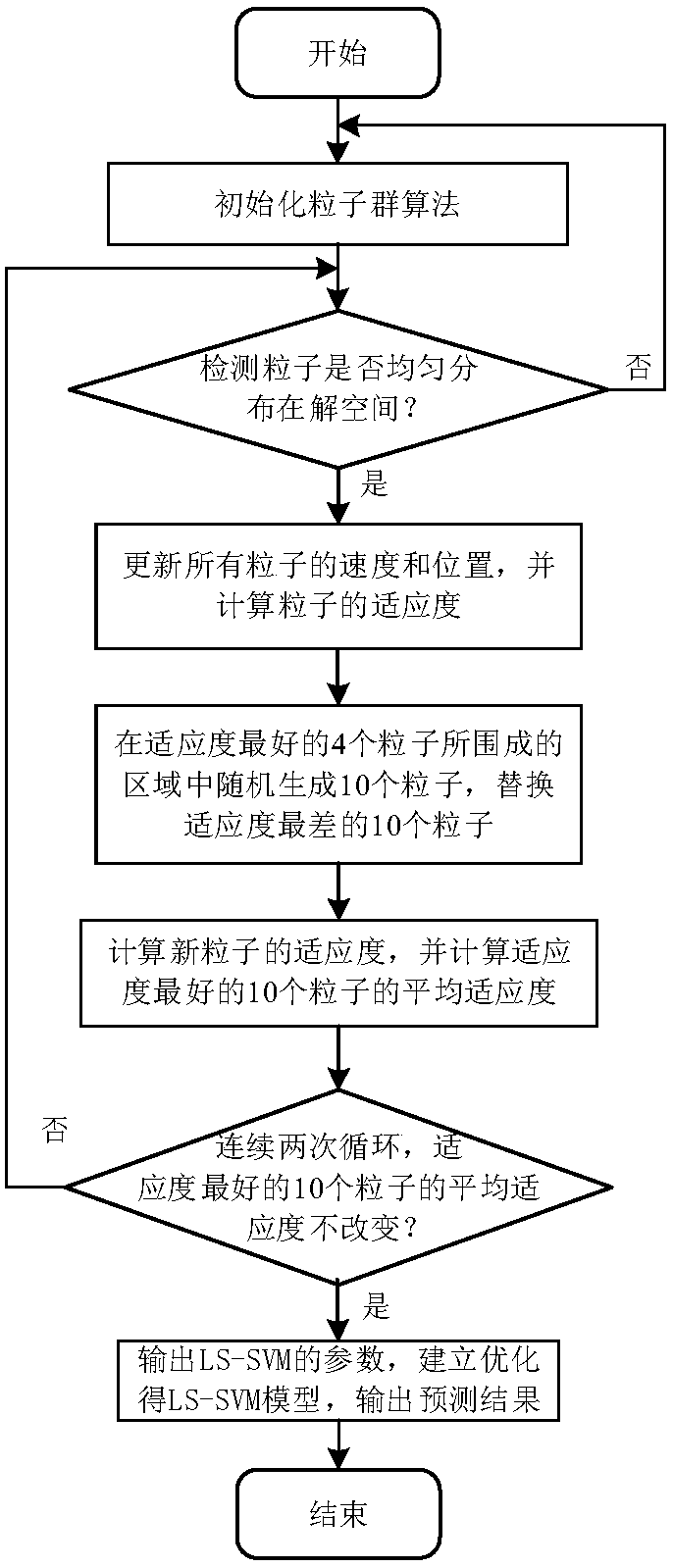
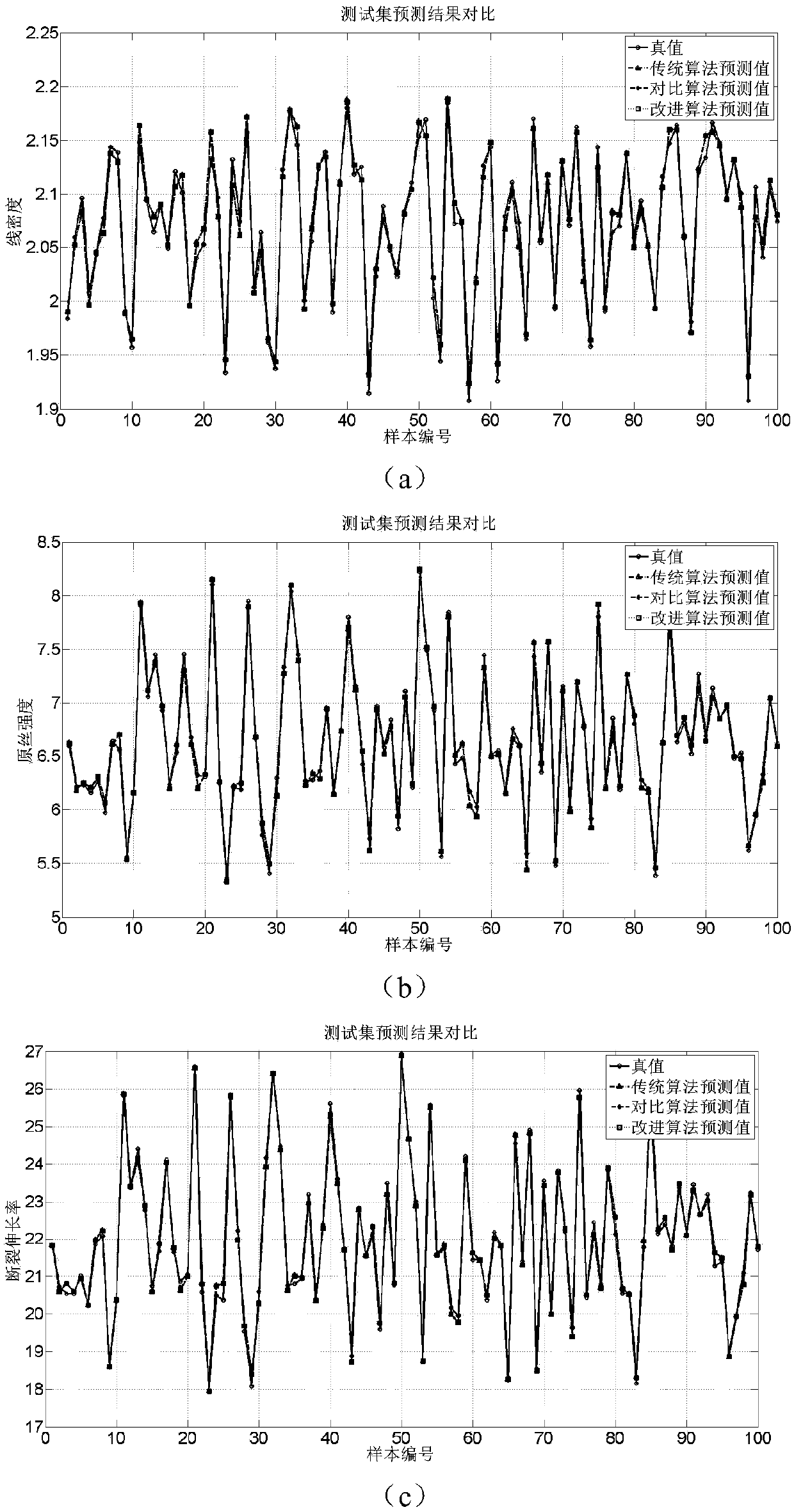
The invention relates to a method for predicting performance indexes in a polyester fiber spinning process, in particular to a method for predicting performance indexes in a polyester fiber spinning process based on a least square support vector machine (LS-SVM) optimized by a particle swarm optimization (PSO) algorithm improved by a power law. The method comprises the following steps of selecting production parameters, including a spinning speed, a spinning temperature, an air blowing temperature and an air blowing speed, in the polyester fiber spinning process as feature information, performing linear function normalization, and establishing an input sample dataset; determining main performance indexes, including half-fold elongation rate, irregularity of the half-fold elongation rate, breaking strength and elongation capability, influencing polyester fiber quality, performing logarithmic function normalization, and establishing an output sample dataset; and building an LS-SVM model according to the input and output sample datasets, adopting a Gauss radial basis function (RBF) as a kernel function of the LS-SVM, and selecting an optimal penalty factor C and a kernel function parameter sigma by using PSO. The PSO process is improved according to the power law, so that the optimization speed can be greatly increased and accurate prediction is realized.
Owner:DONGHUA UNIV
Prediction control method and system for magnetic levitation system
ActiveCN109991850ANo loss of precisionFeasibleAdaptive controlGaussian radial basis functionNon linear dynamic
The invention discloses a prediction control method and system for a magnetic levitation system. By historical data of the magnetic levitation ball system and through adopting a system identificationmethod, an autoregressive model which takes a Gaussian radial basis function network as a coefficient and has an exogenous variable is established to describe nonlinear dynamic characteristics betweenan input voltage of an electromagnetic winding and a position of a steel ball. An ARX model coefficient is fit by an RBF neural network, so that an RBF-ARX model can well depict the nonlinear dynamiccharacteristics of the magnetic levitation ball system. Then, on the basis of a principle of a predictive functional control algorithm, a structure of a control input is determined so as to completerolling optimization and error correction. The predictive functional control algorithm has higher tracking capacity and higher robustness than PID control, and has a smaller online calculation amountand a higher control speed than conventional model prediction control; and when a system set value is a step signal, the control method can implement unbiased tracking.
Owner:CENT SOUTH UNIV
Improved-support-vector-machine-based power load prediction correction method
InactiveCN106372763AImprove forecast accuracyFast convergenceForecastingSupport vector machineGaussian radial basis function
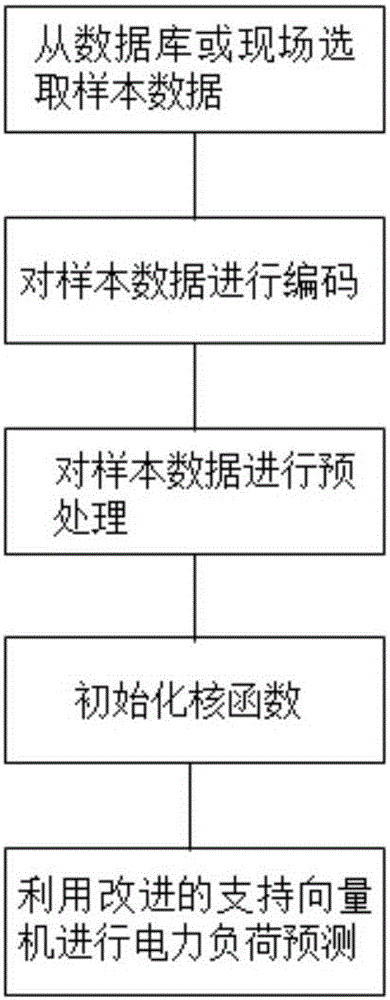
The invention relates to a power load prediction correction method, especially to an improved-support-vector-machine-based power load prediction correction method. With the method, problems that the current and future power demand changes and the power demand development trend can not be reflected accurately and the power load accuracy prediction is low can be solved. Therefore, the invention puts forward an improved-support-vector-machine-based power load prediction correction method. The method comprises: step one, sample data are selected from a database or a field; step two, the sample data are coded; step three, pretreatment is carried out on the coded sample data; step four, a kernel function is initialized; and the sample data after pretreatment are processed by selecting a Gaussian radial basis function; and step five, power load prediction is carried out by using an improved support vector machine. The method is applied to the power load prediction correction field.
Owner:STATE GRID CORP OF CHINA +2
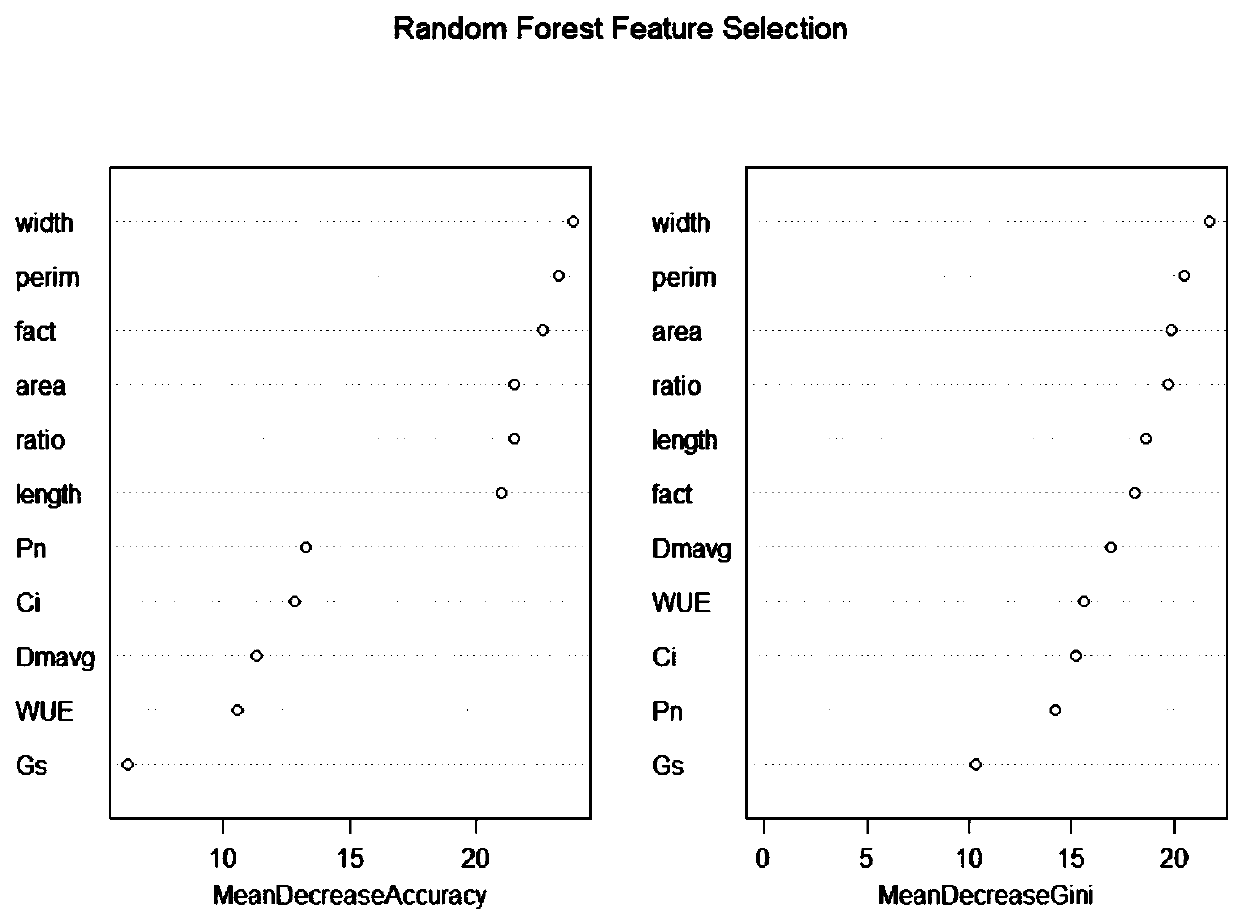
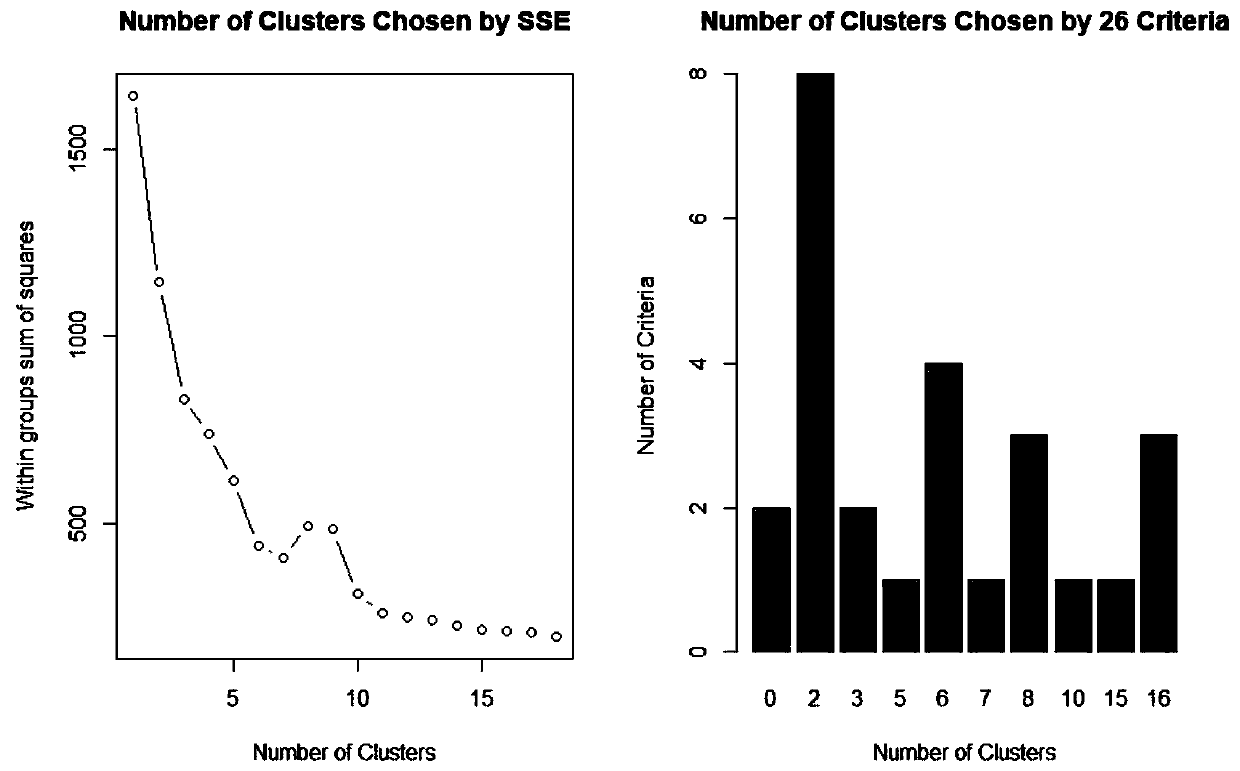
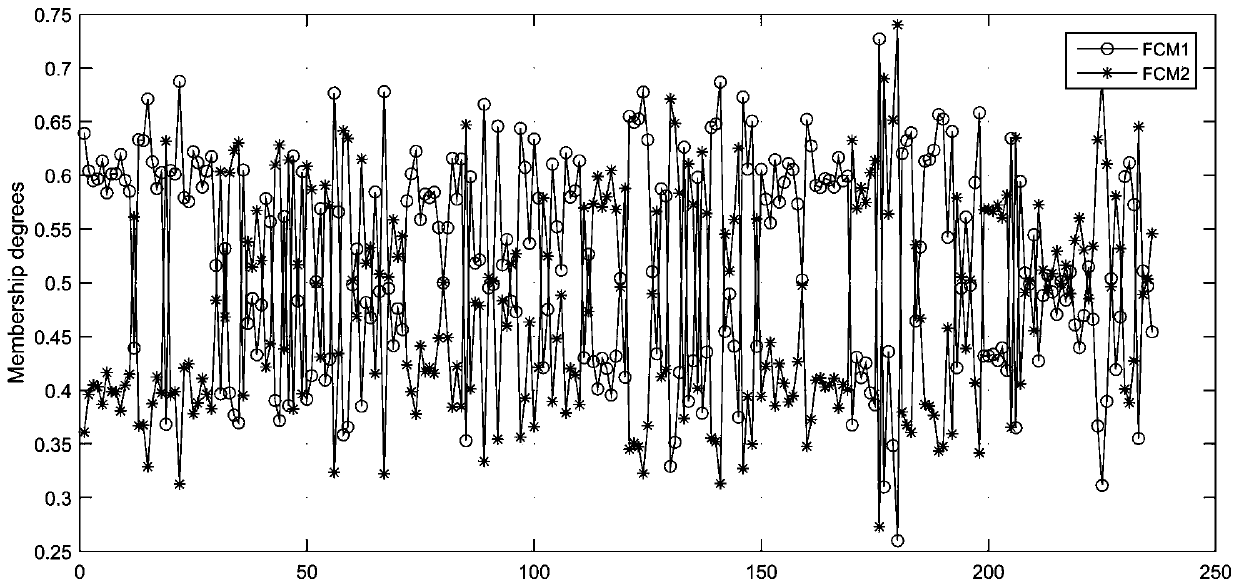
Methods for constructing and predicting leaf trait of woody plant and photosynthetic characteristic model based on DNA methylation level
The invention provides methods for constructing and predicting the leaf trait of a woody plant and a photosynthetic characteristic model based on a DNA methylation level, and belongs to the technicalfield of biological analysis. The predicting method comprises selecting important characteristic variable embodying a geographic position difference based on a random forest, screening out 7 leaf characteristic variables, determining an optimal cluster number, and obtaining each group of cluster leaf samples by using an improved FCM clustering algorithm; according to the correlation between variables and the importance of Enzyme digestion combination obtained by a gradient boosted tree, obtaining an important enzyme digestion combination in each group of cluster leaf samples; by using the DNAmethylation level of the enzyme digestion combination as a regression variable, constructing LS-SVM regression prediction model based on Gaussian radial basis function; inputting the DNA methylation level of important enzyme digestion combination to accurately predict a leaf shape factor, leaf area and a net photosynthetic rate. The method is used for predicting the phenotypic characteristic and the photosynthetic characteristic of the woody plant, and screening individuals of woody plants with excellent traits.
Owner:BEIJING FORESTRY UNIVERSITY
Improved-Fisher-based chemical process fault diagnosis method
ActiveCN106326915AImprove distributionFacilitate fault category classificationCharacter and pattern recognitionGaussian radial basis functionAlgorithm
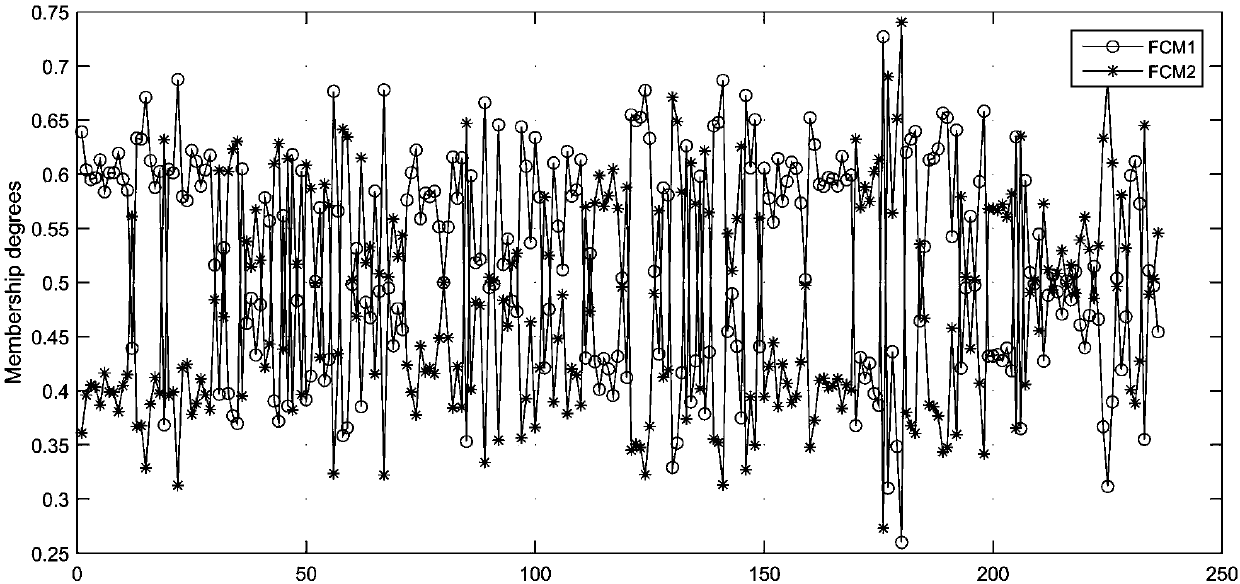
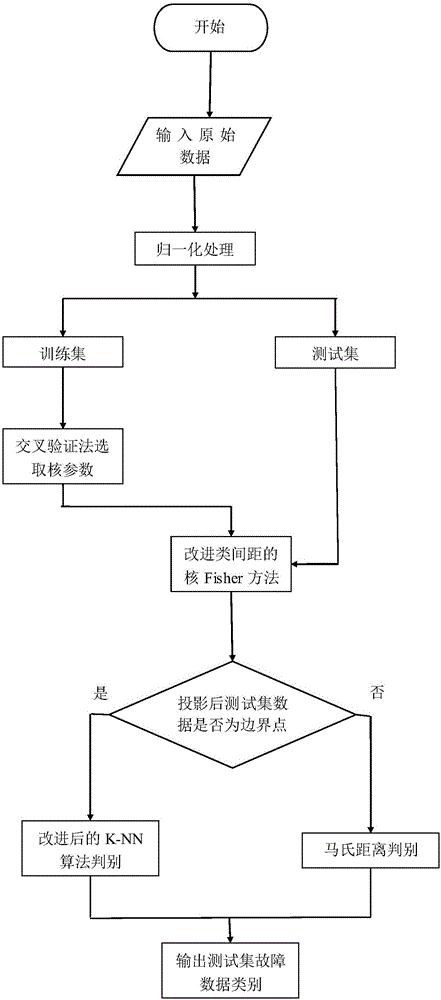
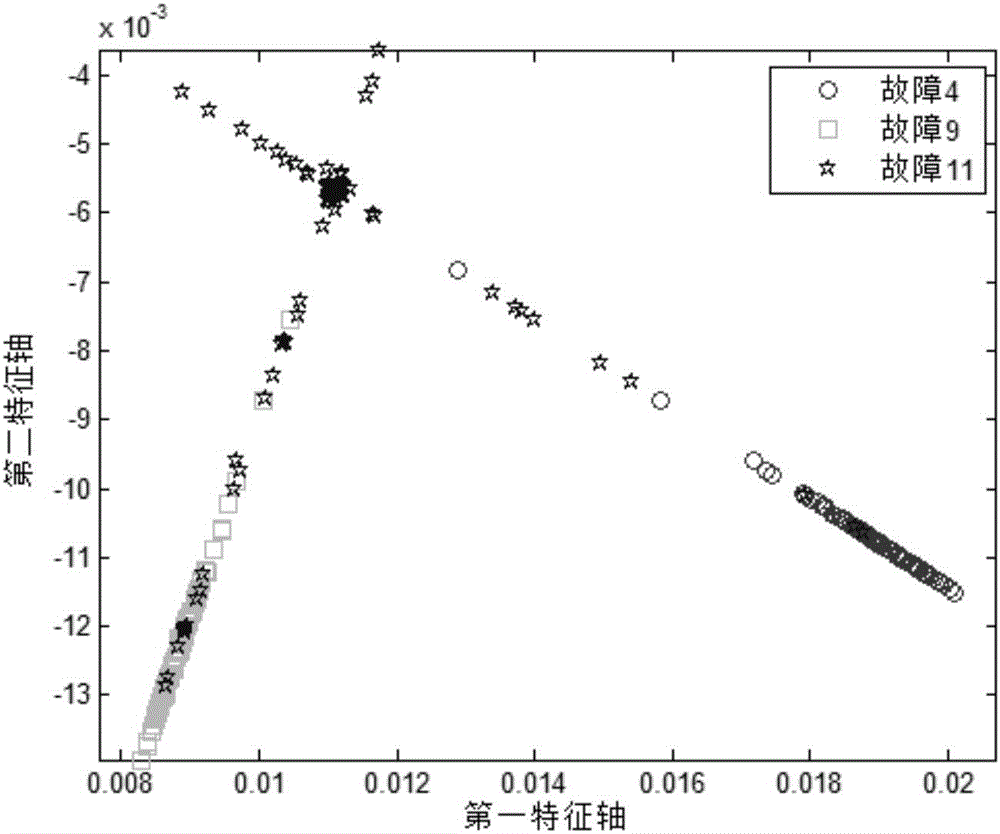
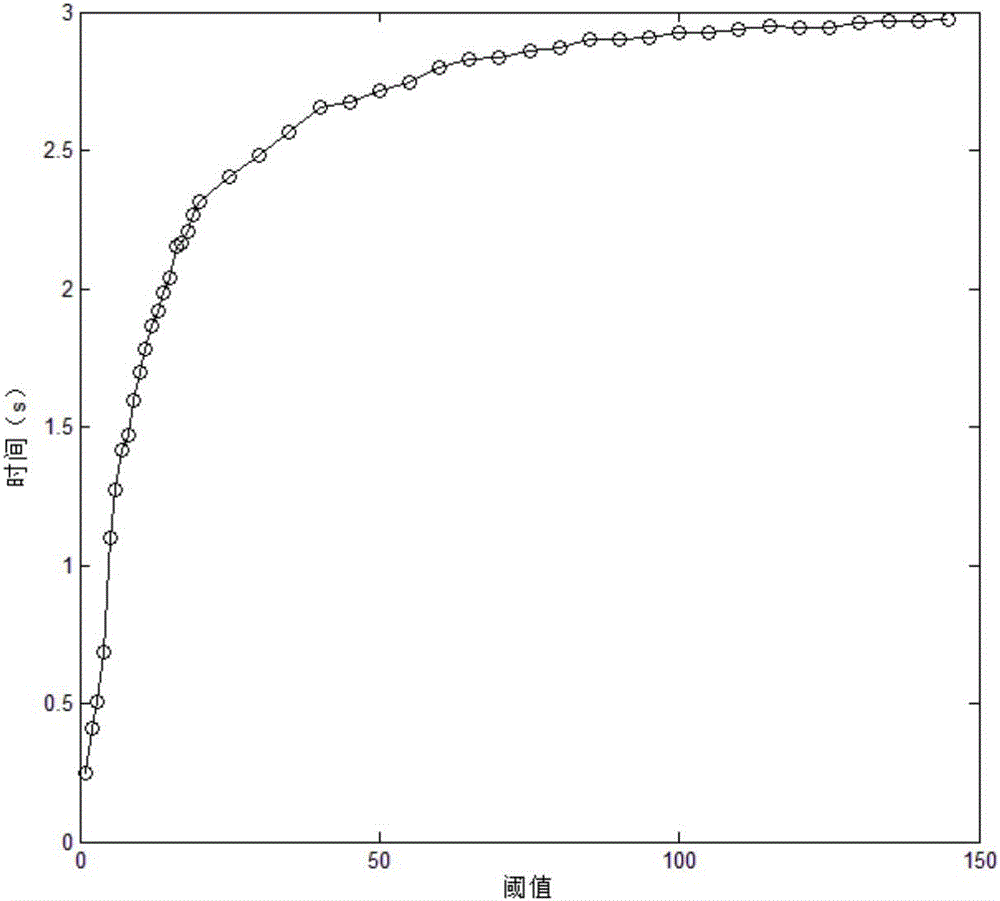
The invention provides an improved-Fisher-based chemical process fault diagnosis method. The method comprises: step one, original chemical process fault diagnosis are collected and normalization processing is carried out on the data, wherein the data are classified into a training set and a testing set; step two, the training seat is inputted into an improved class-separation-distance kernel Fisher method, a threshold parameter is outputted, and a parameter of a Gaussian radial basis function is selected optimally by using a cross validation method; step three, the testing set outputted at the step one is inputted into the improved class-separation-distance kernel Fisher method to carry out projection; and step four, according to the threshold parameter outputted at the step two, whether the data are boundary points after projection at the step three is determined and a fault type is determined by combining an improved K-NN algorithm based on a mahalanobis distance. According to the method, distribution of sampling data in projection space is improved; and with introduction of a boundary threshold parameter and combination of the mahalanobis distance and the improved K-NN algorithm, the classification accuracy of the total samples is increased under the circumstance that the classification time is minimized.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
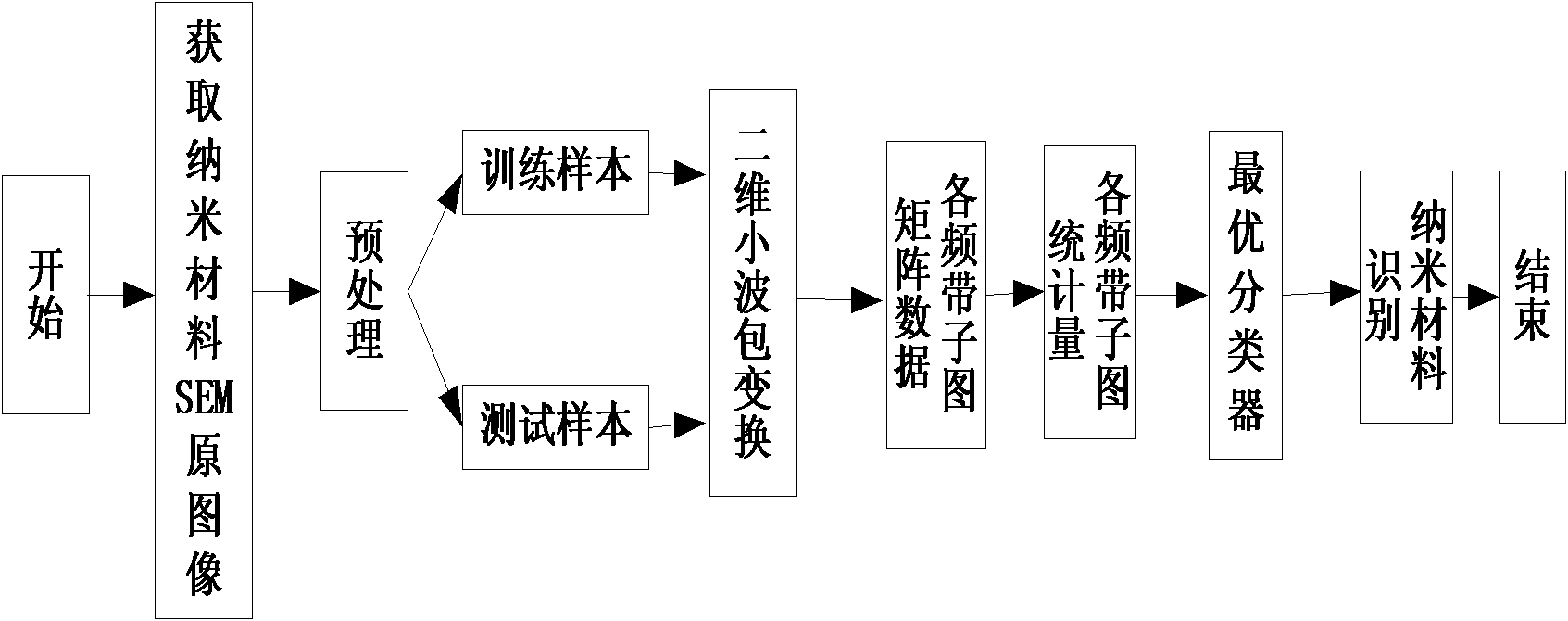
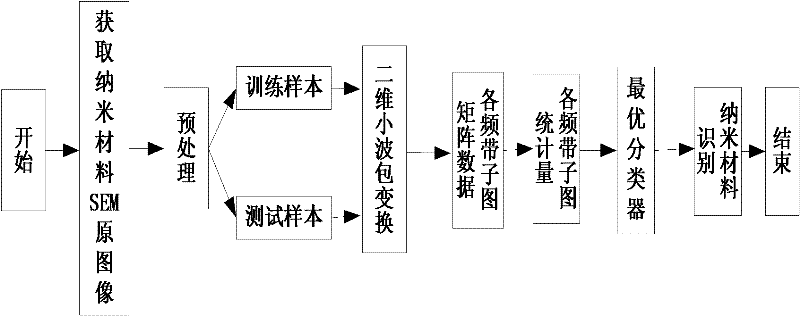
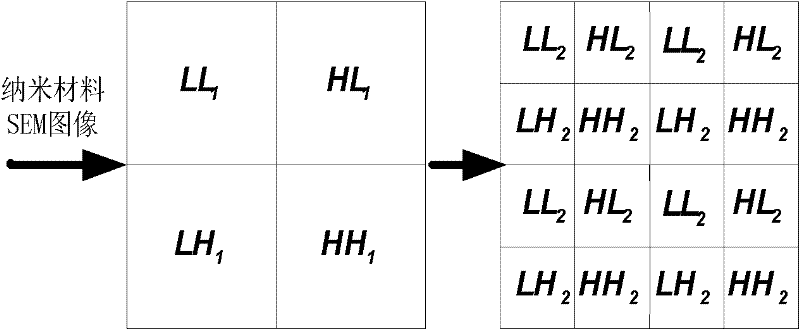
Low-dimensional nano material identification method based on SEM image
ActiveCN102183535ARealize topographical characterizationImplement automatic classificationCharacter and pattern recognitionNanotechnologySupport vector machineGaussian radial basis function
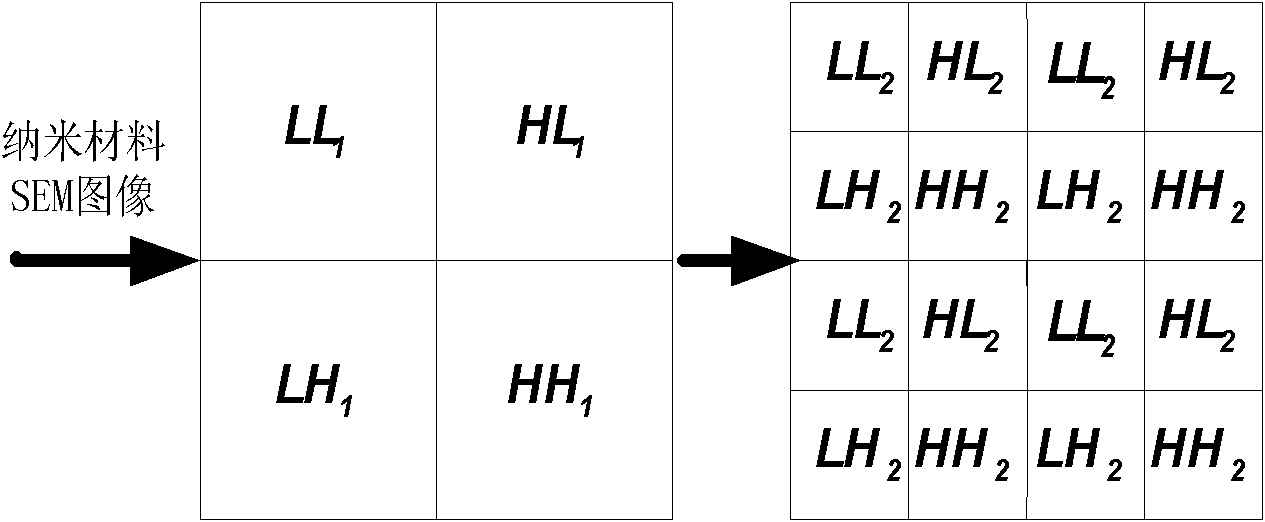
The invention belongs to the crossed technical field of computer mode identification and nano material, and relates to a low-dimensional nano material identification method based on an SEM image. The method comprises the following steps of: (1) preprocessing a known nano material SEM image sample; (2) performing two-dimensional wavelet transformation on the preprocessed image to get sub-image matrixes on different frequency bands; (3) extracting characteristics of the sub-image matrixes on each frequency band, and taking a statistical value of each sub-image matrix as a characteristic value for representing surface texture of the nano material; (4) according to the characteristic value, taking a Gaussian radial basis function as a support vector machine kernel function to find an optimal hyperplane between any two classes, and creating a classification model for different classes of nano materials; (5) extracting a texture characteristic value of the known nano material SEM image sample, and identifying the unknown nano material by voting according to the classification model obtained in the step (4). The low-dimensional nano material identification method based on the SEM image represents and distinguishes different nano material structure types more accurately and effectively, and has the advantages of high accuracy, strong expansibility, high degree of automation and the like.
Owner:NANTONG HUALONG MICROELECTRONICS
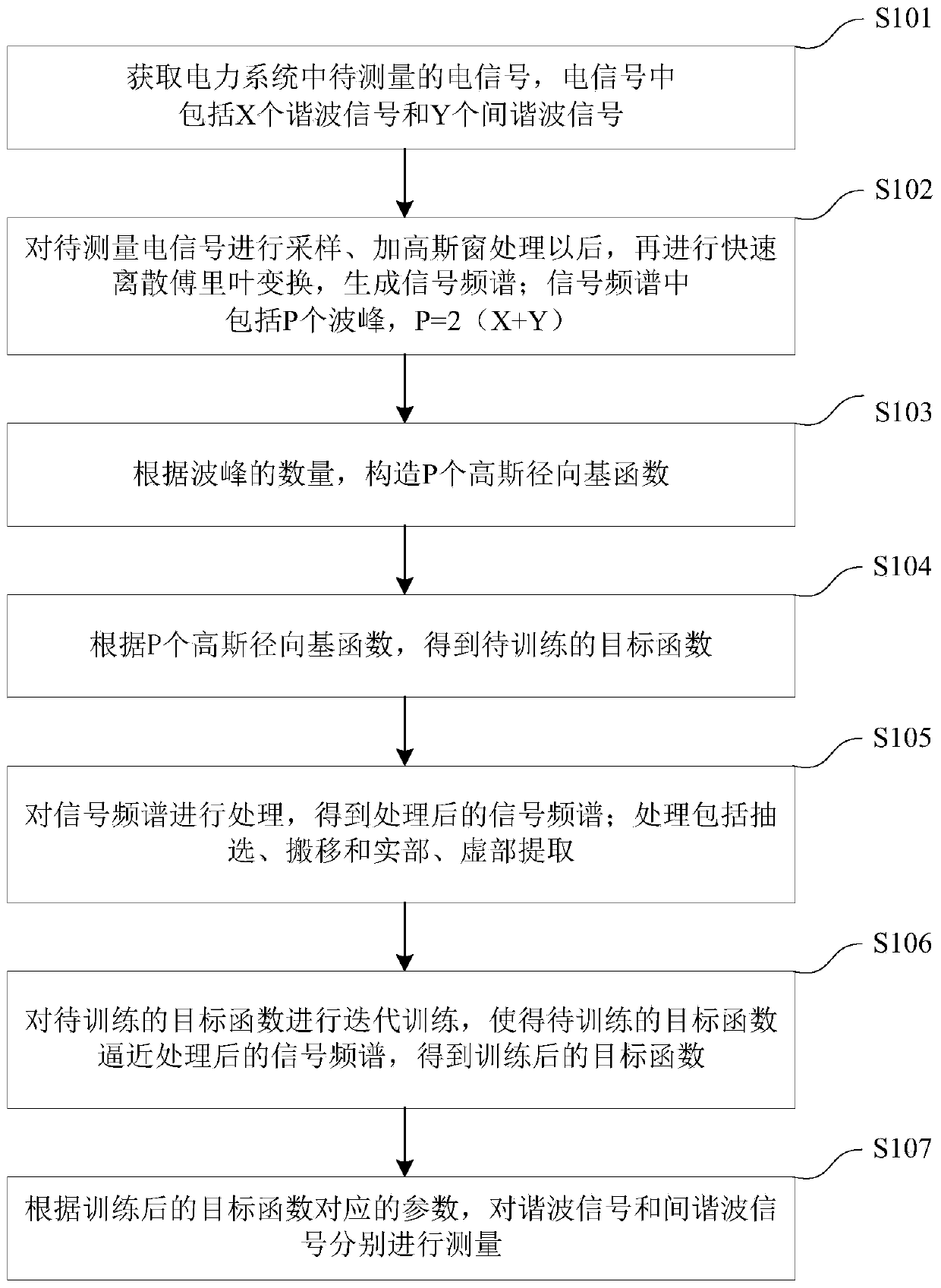
Method and device for measuring harmonic waves and inter-harmonic waves in power system
InactiveCN111579867AAccurate distinctionHigh measurement accuracySpectral/fourier analysisFrequency spectrumElectric power system
The invention provides a method and a device for measuring harmonic waves and inter-harmonic waves in a power system. The method comprises the following steps of: a Gaussian window is added for the time domain of the sampled electric signal in the power system and fast discrete Fourier transform is performed; a signal spectrum is generated, a plurality of Gaussian radial basis functions are constructed according to the number of wave crests in the frequency spectrum; the signal frequency spectrum is processed, iterative training is carried out on the to-be-trained target function, so that theto-be-trained target function approaches the processed signal frequency spectrum, and the harmonic signal and the inter-harmonic signal are respectively measured according to the parameters corresponding to the trained target function. Thus, according to the embodiment of the invention, a series of Gaussian radial basis functions are constructed according to the number of wave crests of the frequency spectrum after fast Fourier transform, the frequency spectrum generating the inter-spectral interference is approximated by utilizing linear superposition of the Gaussian radial basis functions, harmonic and inter-harmonic components generating the main lobe interference in the electric signal can be accurately distinguished, and the measurement precision is relatively high.
Owner:YUNNAN POWER GRID CO LTD ELECTRIC POWER RES INST
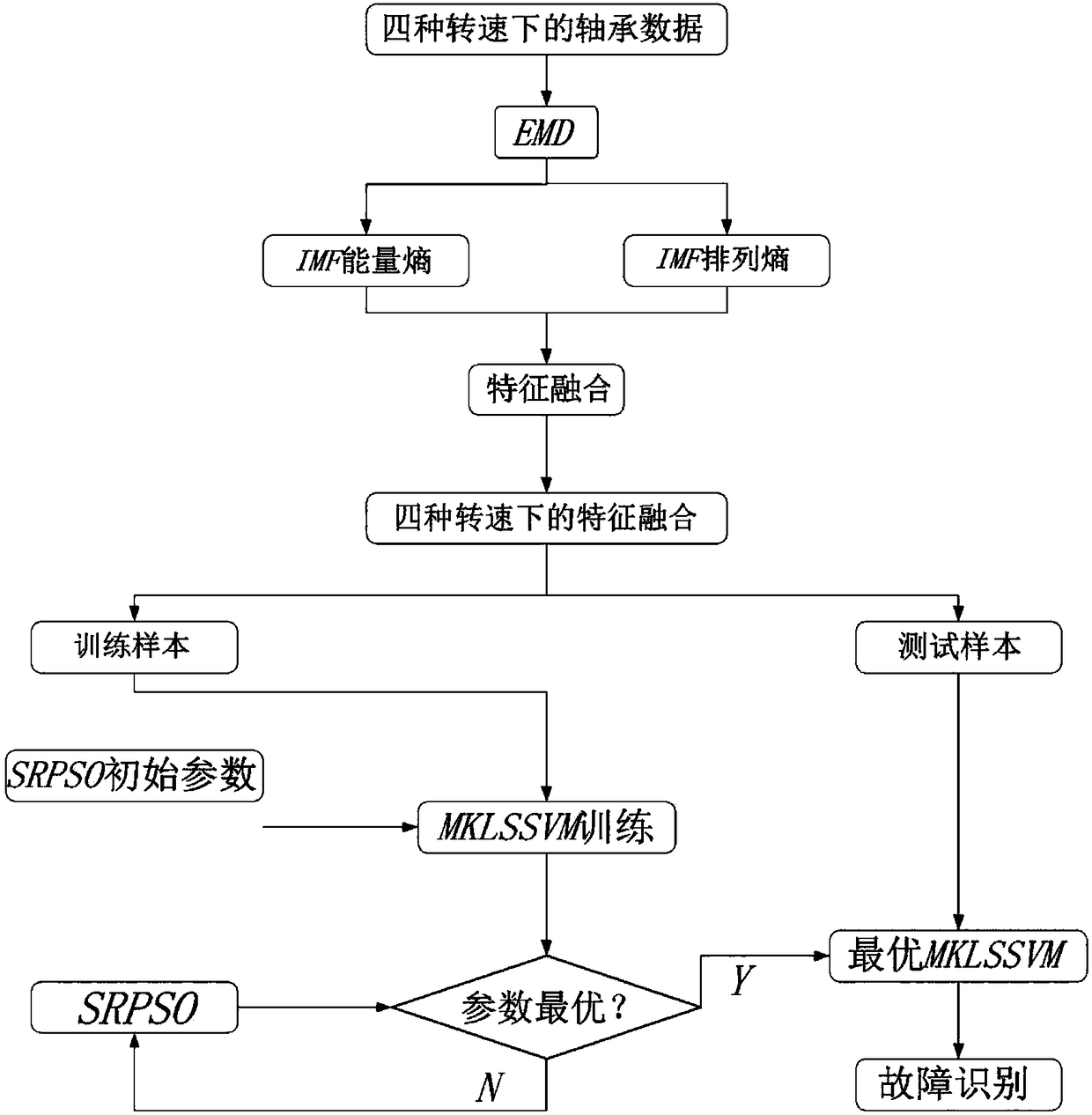
Method for optimizing multi-kernel multi-feature fusion support vector machine and identifying bearing fault
ActiveCN108062564AImprove the accuracy of fault identificationHigh precisionCharacter and pattern recognitionArtificial lifeLeast squares support vector machineEngineering
The invention relates to a method for optimizing a multi-kernel multi-feature fusion support vector machine and identifying a bearing fault. The method comprises a step of selecting bearing vibrationsignals collected under a single sensor, a step of decomposing bearing vibration signals at different rotational speeds by EMD to obtain IMF energy entropy and IMF permutation entropy, a step of extracting IMF energy entropy and IMF permutation entropy at different rotation speeds and fusing the IMF energy entropy and IMF permutation entropy to obtain fusion features including different rotationalspeed information for support vector machine training samples so as to obtain the multi-kernel multi-feature fusion support vector machine which is adapted to fault identification at different rotation speeds, a step of integrating Gaussian radial basis function kernel and polynomial function kernel performance, allowing the training samples to be in linear regression from a nonlinear function space to high-dimensional space mapping such that the training samples are classified according to different characteristics, forming a multi-kernel least square support vector machine, and enabling thesupport vector machine to identify a fault feature under a variable load, and a step of carrying out parameter optimization on the training samples with a self-adjusting particle swarm algorithm withstrong convergence, comparing the training samples and a test sample, and identifying the bearing fault.
Owner:INNER MONGOLIA UNIV OF SCI & TECH
Chinese text classification method
InactiveCN108509471AImprove accuracyImprove recallSemantic analysisSpecial data processing applicationsHidden layerGaussian radial basis function
The invention provides a Chinese text classification method. The method includes the following steps: (1) text preprocessing, (2) feature representation and feature extraction, (3) classifier design,and (4) performance indicators. According to the method, a new RBF neural-network algorithm is employed, K-means is used to derive a center point and width of hidden items through Gaussian radial basis function, output results obtained by a hidden layer are combined, thus a classification result is obtained, values of an accuracy rate, a recall rate and F measurement of the algorithm are very high, and a classification effect is good.
Owner:SUZHOU CHUNQING INTELLIGENT TECH CO LTD
A grid-free lattice Boltzmann method based on semi-Lagrangian and a radial basis function
PendingCN109918744ATo achieve the purpose of solving the flow problemSpecial data processing applicationsGaussian radial basis functionSupport point
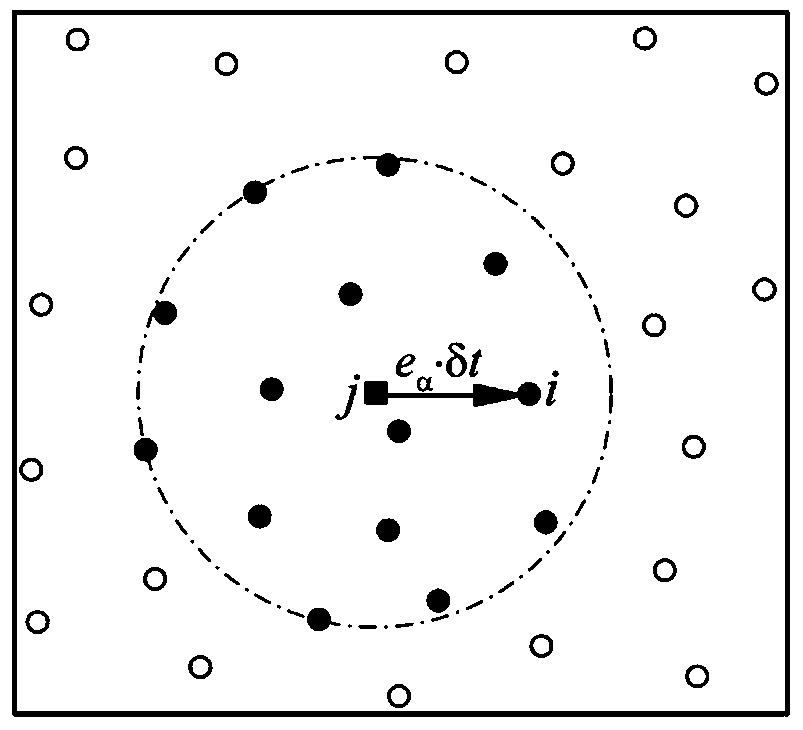
The invention discloses a grid-free lattice Boltzmann method based on semi-Lagrangian and a radial basis function, and belongs to the field of computational fluid mechanics, which enables the latticeBoltzmann method (LBM) to get rid of the limitation of uniform grids by introducing a semi-Lagrangian method and a radial basis function interpolation method, and further expands the application of the LBM in complex flow problems. The method comprises the following steps: firstly, introducing an SL method into a lattice Boltzmann method, and finding a migration starting point, namely x-e Alpha Delta t, obtaining a distribution function of a starting point (x-e Alpha Delta t) by introducing a local RBF interpolation method; According to the local RBF interpolation method, (a relation is shownin the description), wherein phi (x) is a target position function value, Phi (|| x-xi ||) is a radial basis function, and | | x-xi|| is a Euclidean norm, p (x) is a multivariate polynomial, n is thenumber of supporting points, m is the order of the multivariate polynomial, and m is an interpolation coefficient.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
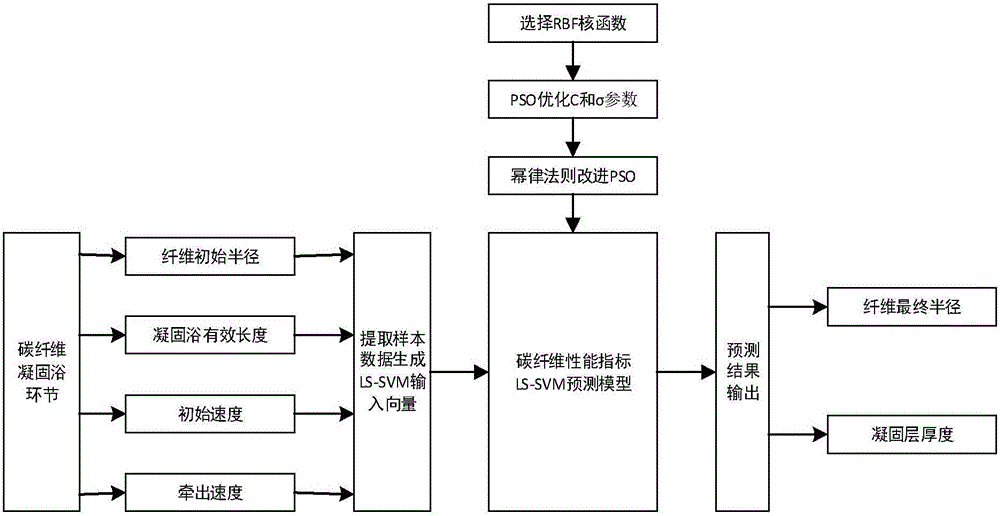
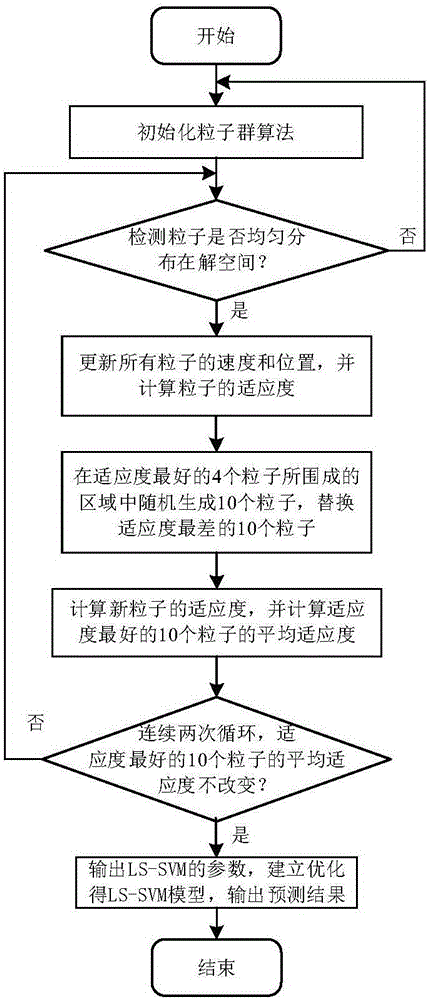
Method for predicting coagulation bath link performance index in carbon fiber precursor production process
InactiveCN106447065AEasy to filterEasy to replaceForecastingManufacturing computing systemsFiberGaussian radial basis function
The invention relates to a method for predicting a coagulation bath link performance index in a carbon fiber precursor production process and especially relates to a method for predicting a coagulation bath link performance index in a carbon fiber precursor production process of a least square support vector machine (LS-SVM) optimized by particle swarm optimization (PSO) improved based on a power-law rule. The method comprises the following steps: a fiber initial radius, a coagulation bath effective length, an initial speed and a pulling speed of a coagulation bath link in the carbon fiber precursor production process are selected as feature information, and an input sample data set is established after linear function normalization is performed; major performance indexes influencing carbon fiber quality, i.e., a fiber final radius and a coagulation layer thickness are determined, and an output sample data set is established after logarithm function normalization is performed; and according to the input-output sample data sets, establishing an LS-SVM model, by taking a Gaussian radial basis function (RBF) as a nucleus function of the LS-SVM, an optimal punishment factor C and a nucleus function parameter sigma are selected by use of the PSO; and the searching optimization process of the PSO is improved according to the power-law rule such that the searching optimization speed can be greatly improved and accurate prediction is realized.
Owner:DONGHUA UNIV
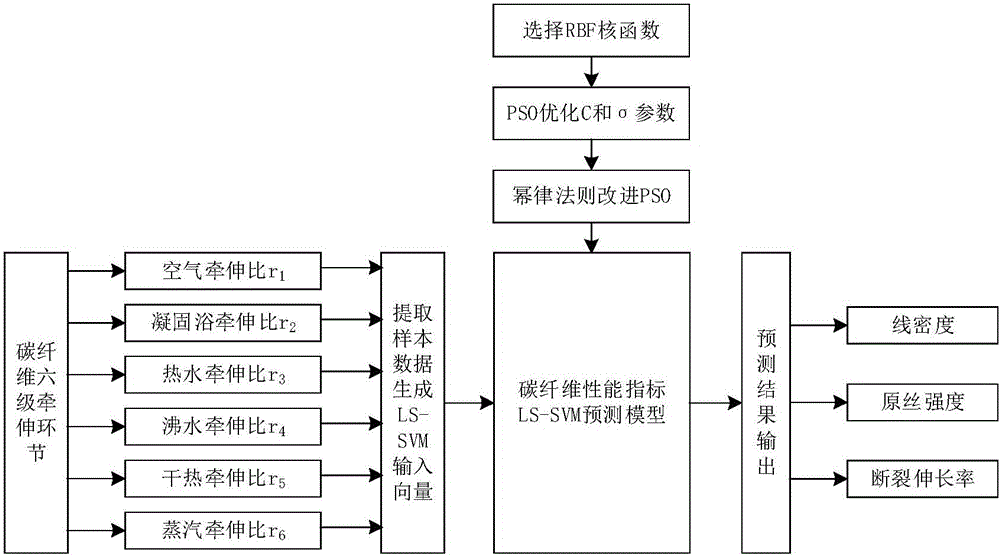
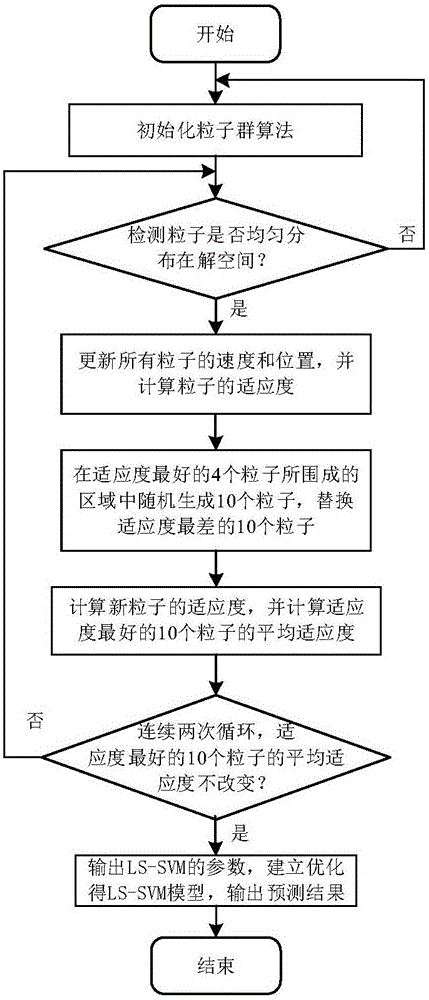
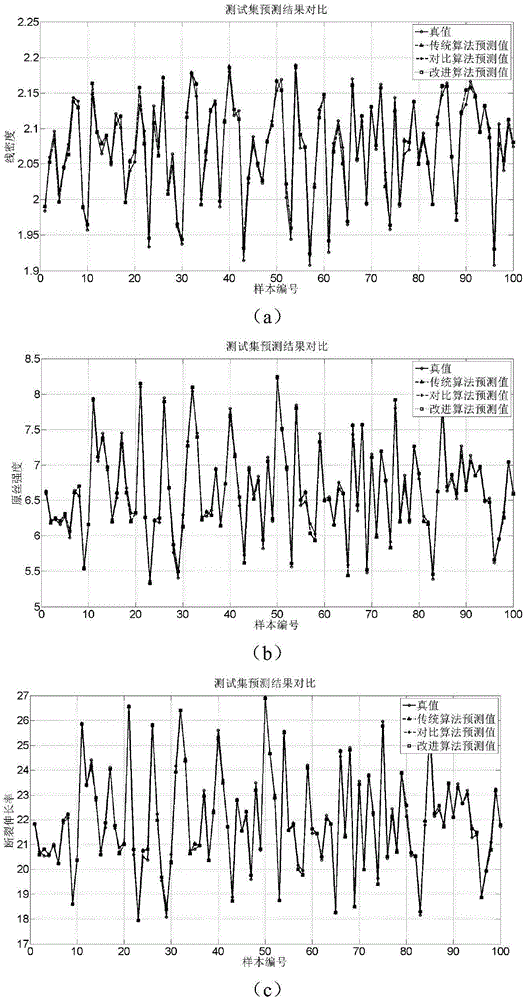
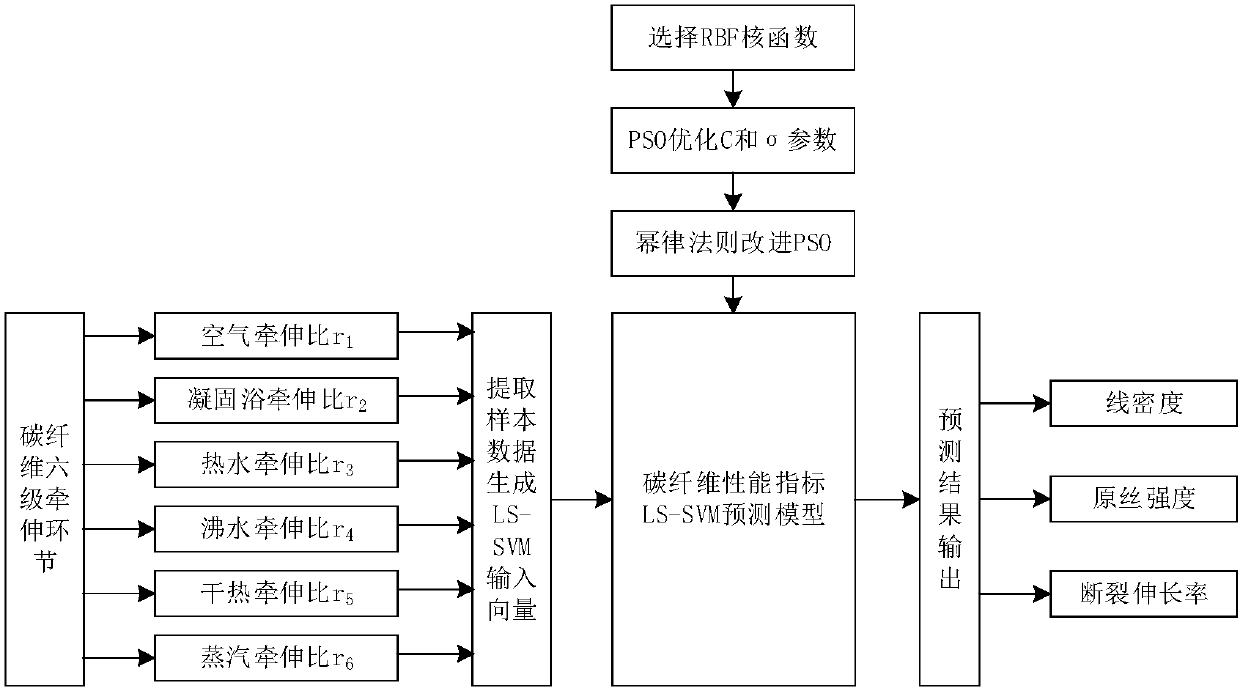
Method for predicting performance indexes of drafting link in carbon fiber precursor production process
The invention relates to a method for predicting performance indexes of a drafting link in a carbon fiber precursor production process, in particular to a method for predicting performance indexes of a drafting link in a carbon fiber precursor production process based on a least square support vector machine (LS-SVM) optimized by a particle swarm optimization (PSO) algorithm improved by a power law. The method comprises the following steps of selecting a six-stage draft ratio of the drafting link in the carbon fiber precursor production process as feature information, performing linear function normalization, and establishing an input sample dataset; determining main performance indexes, including linear density, precursor strength and breaking elongation rate, influencing carbon fiber quality, performing logarithmic function normalization, and establishing an output sample dataset; and building an LS-SVM model according to the input and output sample datasets, adopting a Gauss radial basis function (RBF) as a kernel function of the LS-SVM, and selecting an optimal penalty factor C and a kernel function parameter sigma by using PSO. The PSO process is improved according to the power law, so that the optimization speed can be greatly increased and accurate prediction is realized.
Owner:DONGHUA UNIV
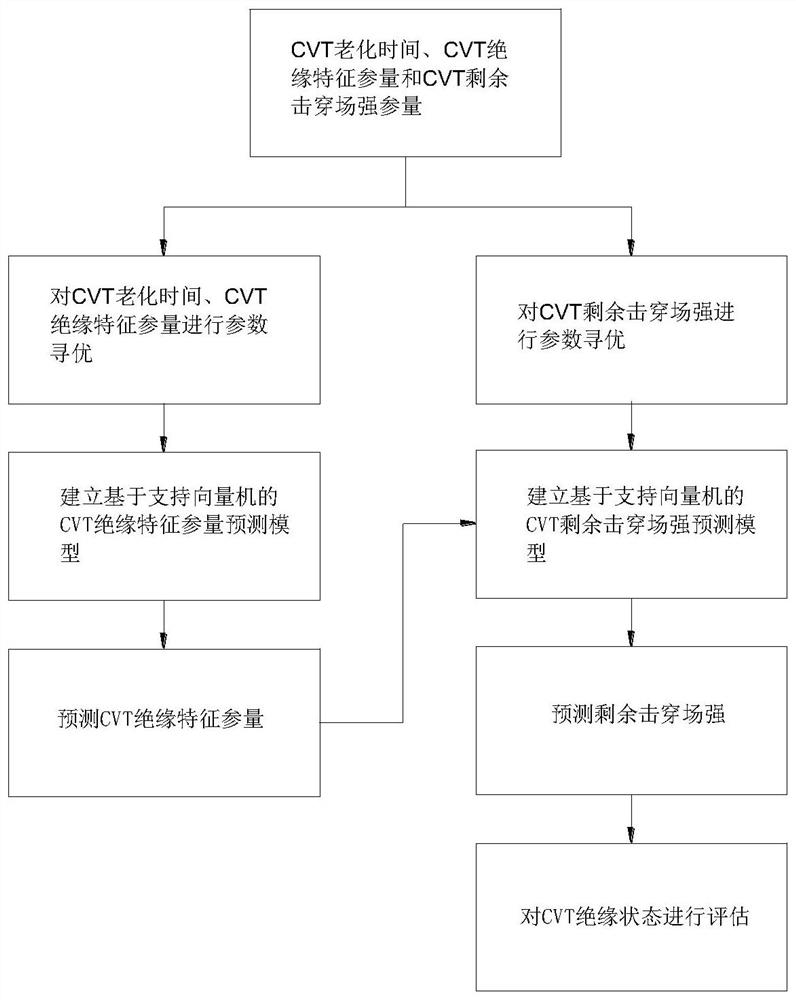
Capacitive voltage transformer multi-parameter insulation state evaluation method and system
PendingCN113884839ARealize evaluationImprove the level of intelligent operation and maintenanceTesting dielectric strengthGaussian radial basis functionPower grid
The invention discloses a capacitive voltage transformer multi-parameter insulation state evaluation method and system, and equipment, which relate to the technical field of power transmission and transformation equipment. The capacitive voltage transformer multi-parameter insulation state evaluation method comprises the following steps of: acquiring sample data, and subjecting the sample data to normalization processing, wherein the sample data comprise CVT aging time, CVT insulation characteristic parameters and CVT residual breakdown field intensity parameters; establishing an insulation characteristic parameter prediction model by adopting a linear kernel function to obtain a CVT insulation parameter prediction value; adopting a Gaussian radial basis function to establish a residual breakdown field intensity prediction model, and acquiring a residual breakdown field intensity predicted value; and evaluating an insulation state of a CVT according to the residual breakdown field intensity predicted value. According to the capacitive voltage transformer multi-parameter insulation state evaluation method provided by the invention, by establishing the mapping relation between the CVT insulation characteristic parameters and the residual breakdown field intensity, the evaluation of the CVT insulation state is realized, and the safe operation of the CVT and the safe reliability of a power grid are ensured.
Owner:STATE GRID SICHUAN ELECTRIC POWER CORP ELECTRIC POWER RES INST
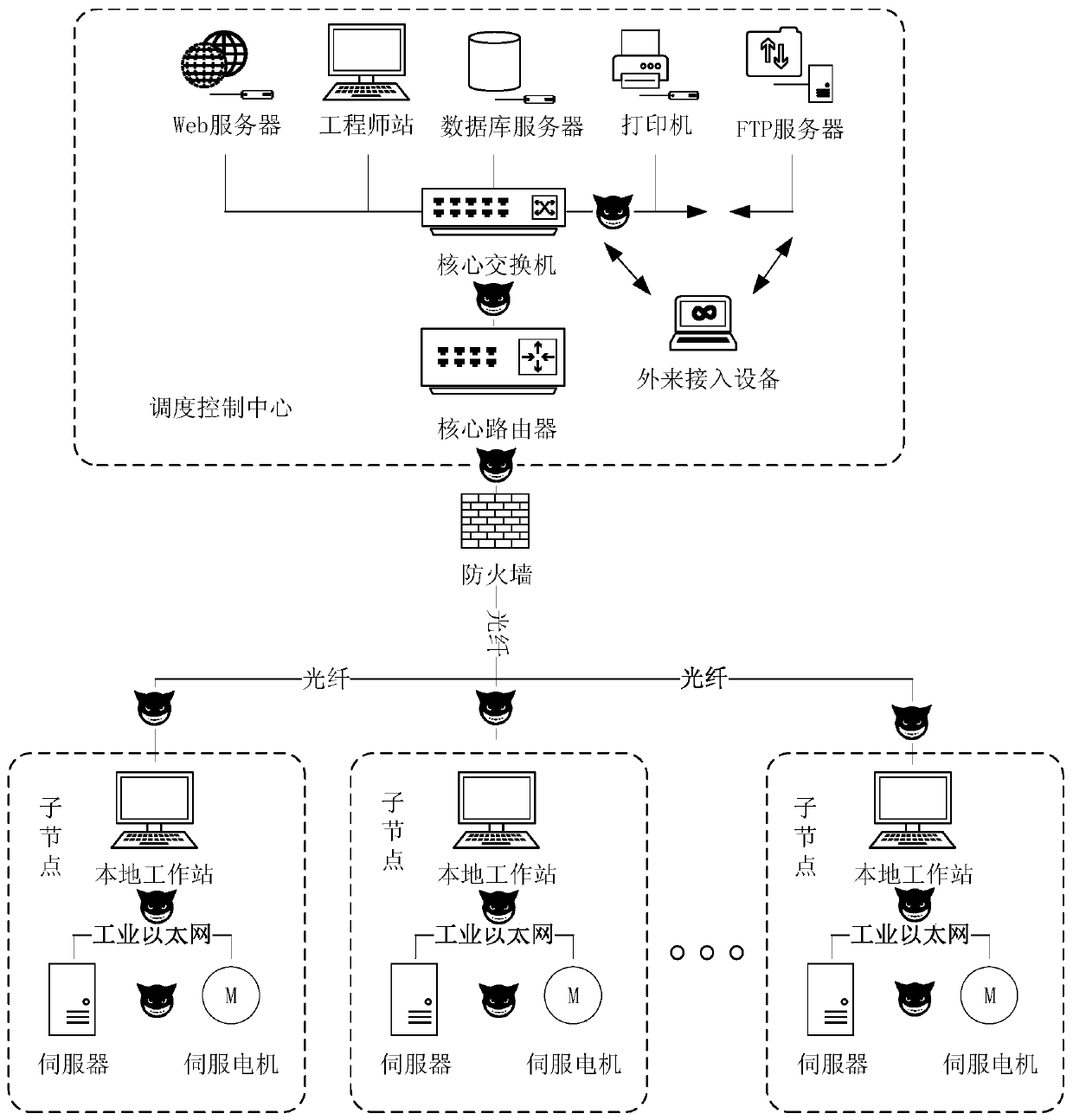
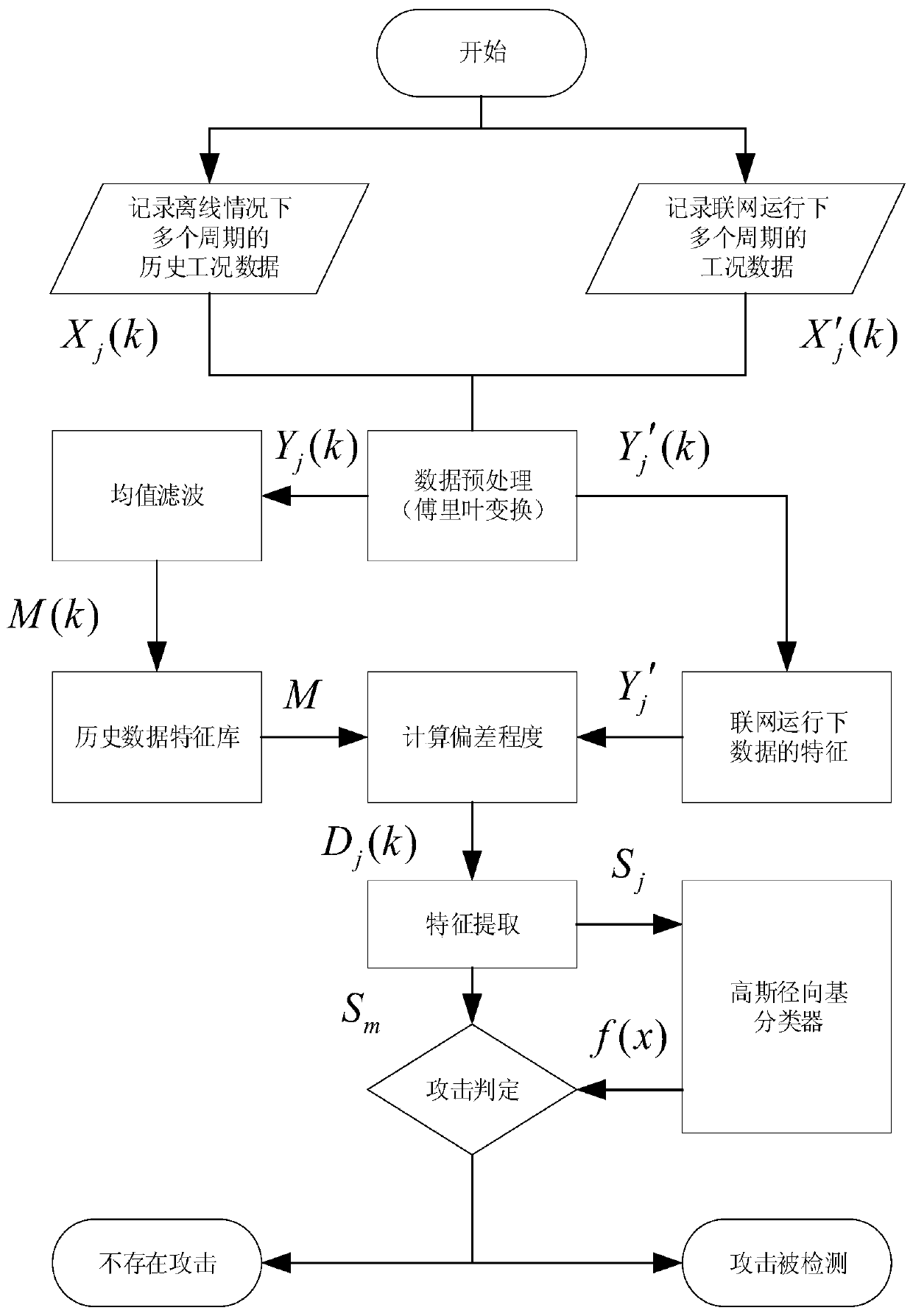
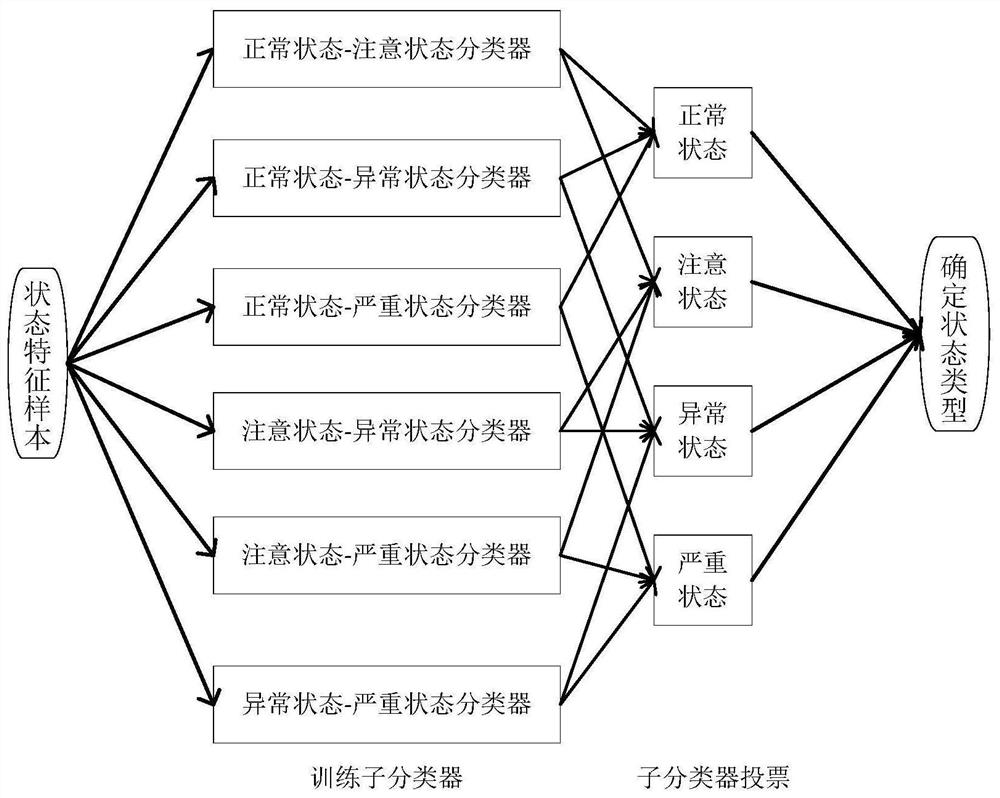
Networked numerical control system man-in-the-middle attack detection method based on Gaussian radial basis function classifier
ActiveCN110311898AAddress professional attacksSimple theoretical frameworkCharacter and pattern recognitionTransmissionSupport vector machineGaussian radial basis function
The invention discloses a networked numerical control system man-in-the-middle attack detection method based on a Gaussian radial basis function classifier, and the method comprises the steps: firstly, analyzing the physical sensor information of a numerical control system from the perspective of a control level; then, starting from the perspective of data driving, considering the data of the industrial control system under the offline condition as normal working condition data, and further analyzing the working condition data under the online condition by taking the normal working condition data as a reference; taking the deviation degree between the working condition data and the historical working condition data under the online condition as sample data; then, starting from the perspective of statistics, taking the mean value and the variance as feature information of the sample data; and finally, starting from the perspective of a machine learning method, training a support vectormachine based on a Gaussian radial basis function to obtain a classifier, and achieving correct classification of attacks. The method can solve the problem that a traditional IT security detection scheme is difficult to detect professional attacks; and the theoretical framework is simple, easy to implement and good in generalization capability.
Owner:ZHEJIANG UNIV OF TECH
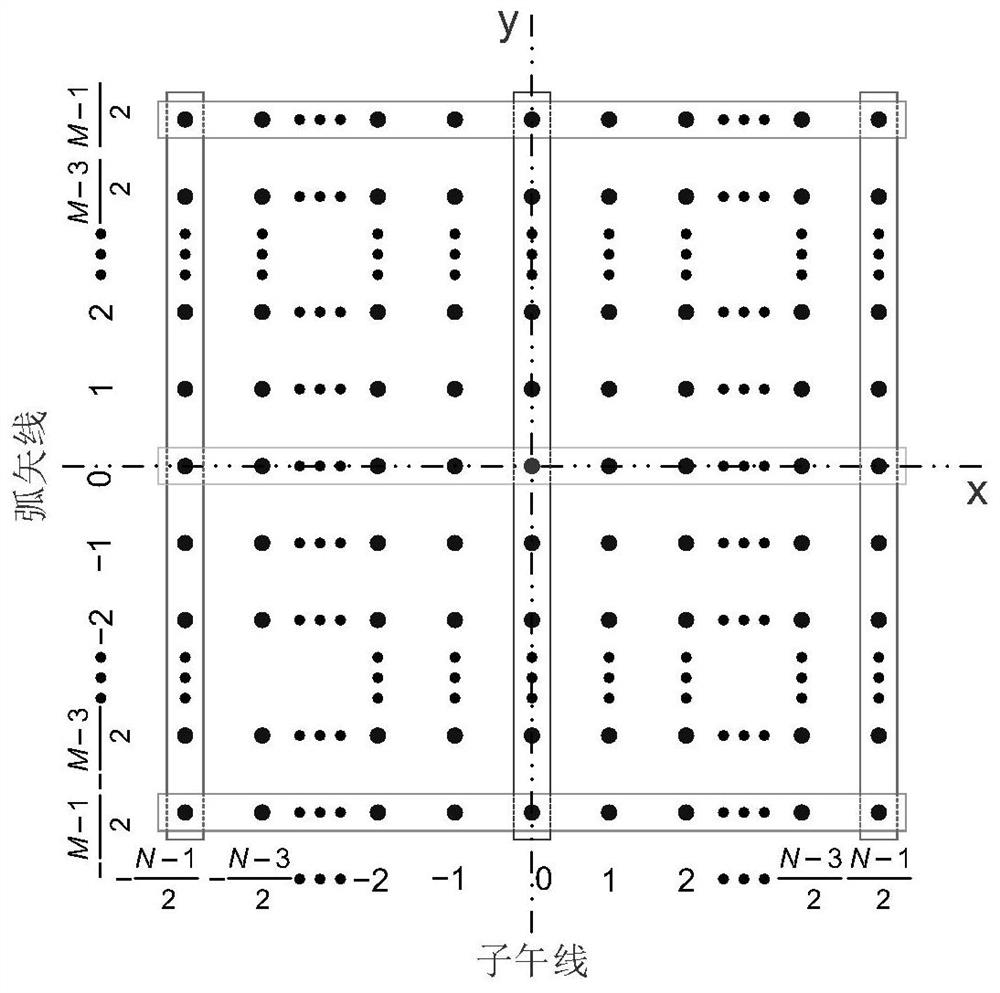
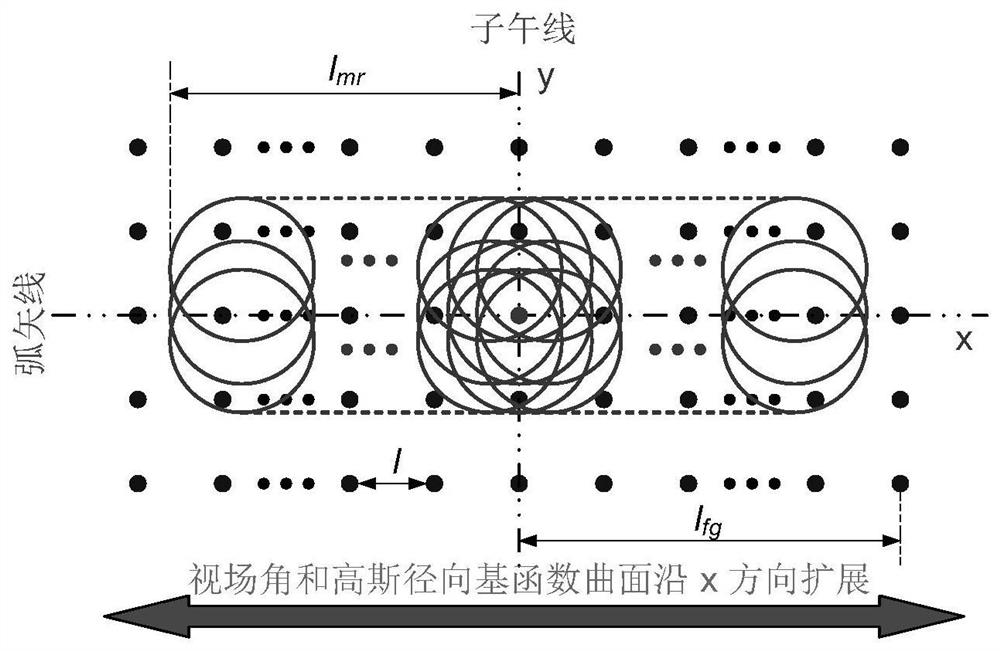
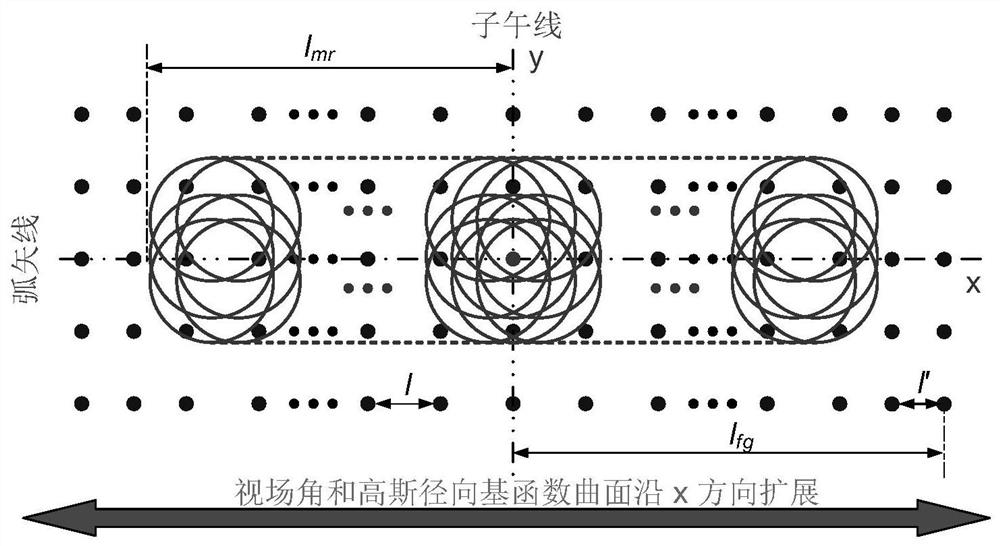
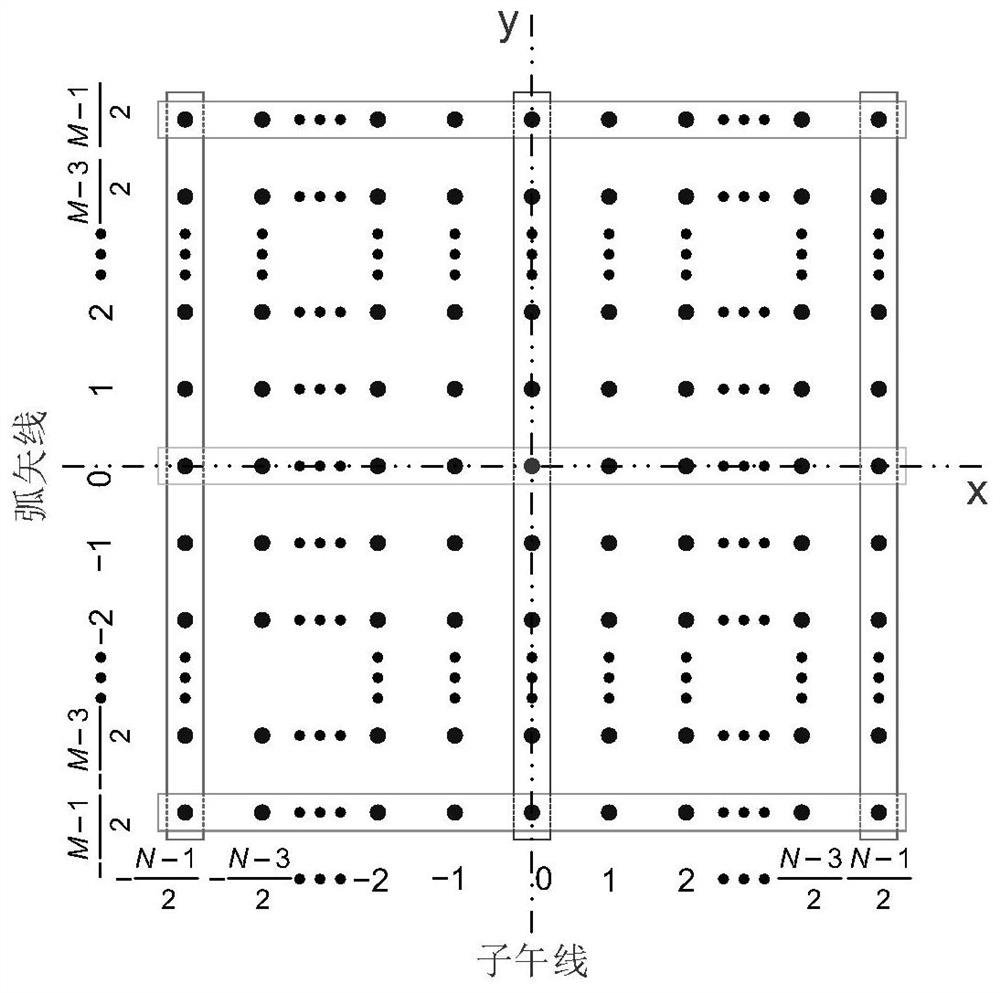
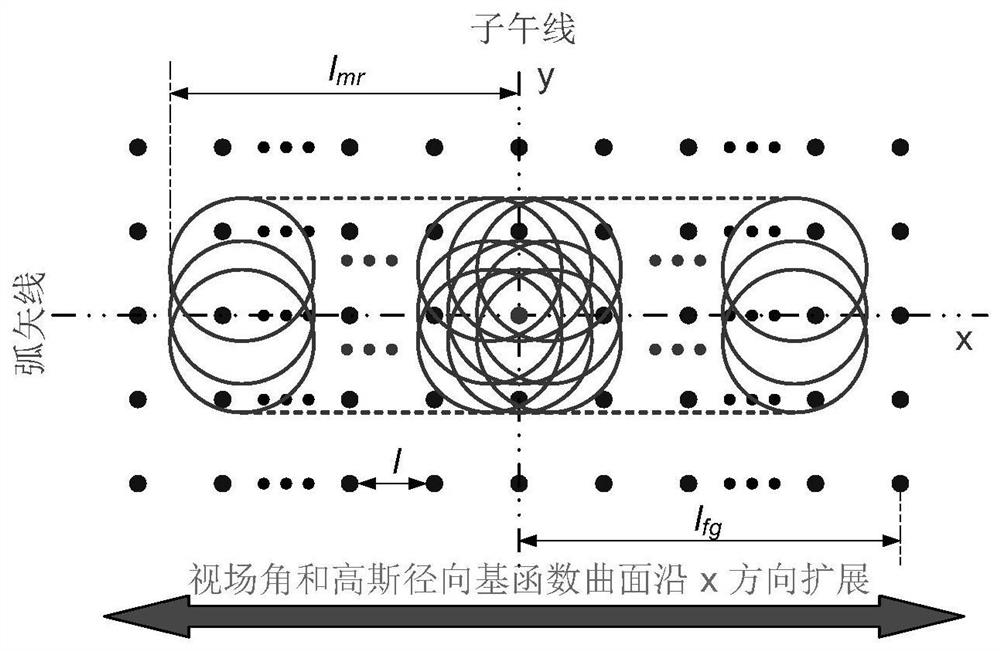
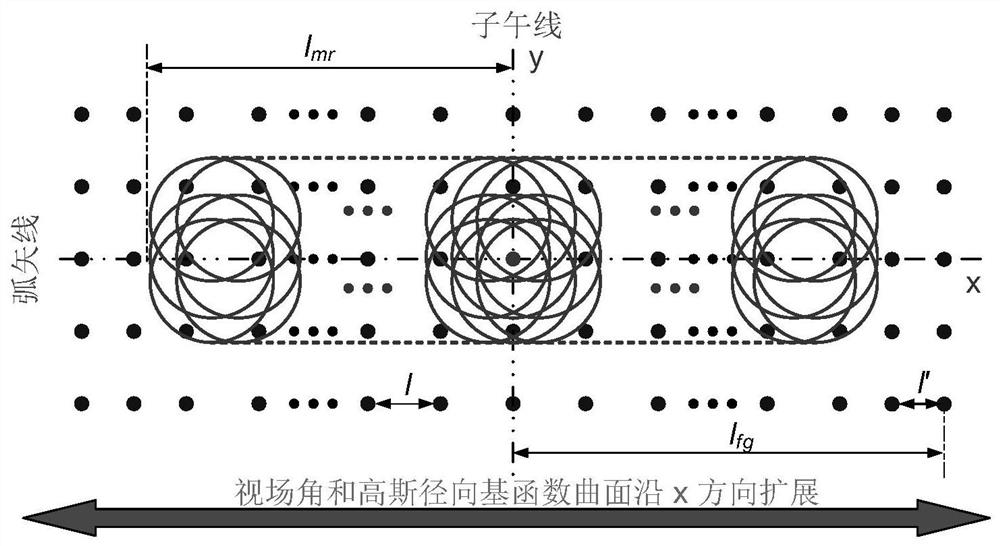
Imaging system design method based on Gaussian radial basis function curved surface
ActiveCN113126289ASimple methodEasy to implementCharacter and pattern recognitionOptical elementsGaussian radial basis functionGaussian function
The invention discloses an imaging system design method based on a Gaussian radial basis function curved surface. An optical system with a field of view smaller than a required value serves as a design starting point, then the field of view is gradually enlarged, based on the thought of field of view expansion and Gaussian continuation, new Gaussian functions are sequentially added to the edge of a curved surface along with expansion of the field of view, the size of the curved surface is gradually expanded, and an imaging system finally meeting design indexes is obtained through progressive optimization. The method is simple, easy to implement and particularly suitable for design of a large-field-of-view imaging optical system. According to the method, convenience is provided for an actual imaging system to apply the Gaussian radial basis function curved surface, the method is convenient, easy and convenient to use and high in applicability, and for free-curved surface imaging systems of various applications and various system structures, the method can be used for gradually completing system design from a simple system as a starting point.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
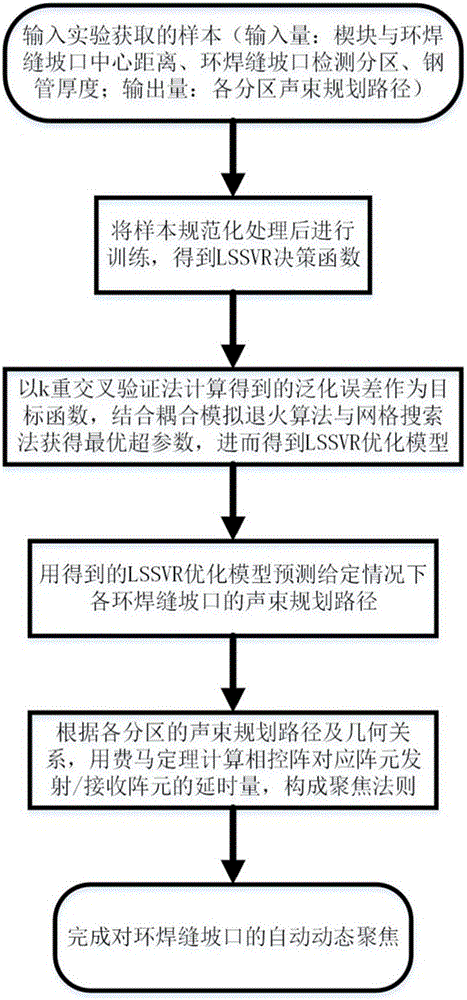
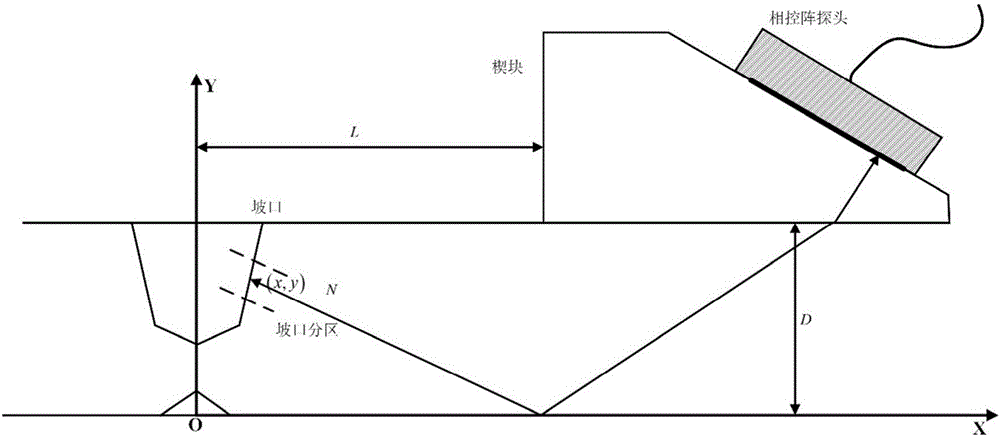
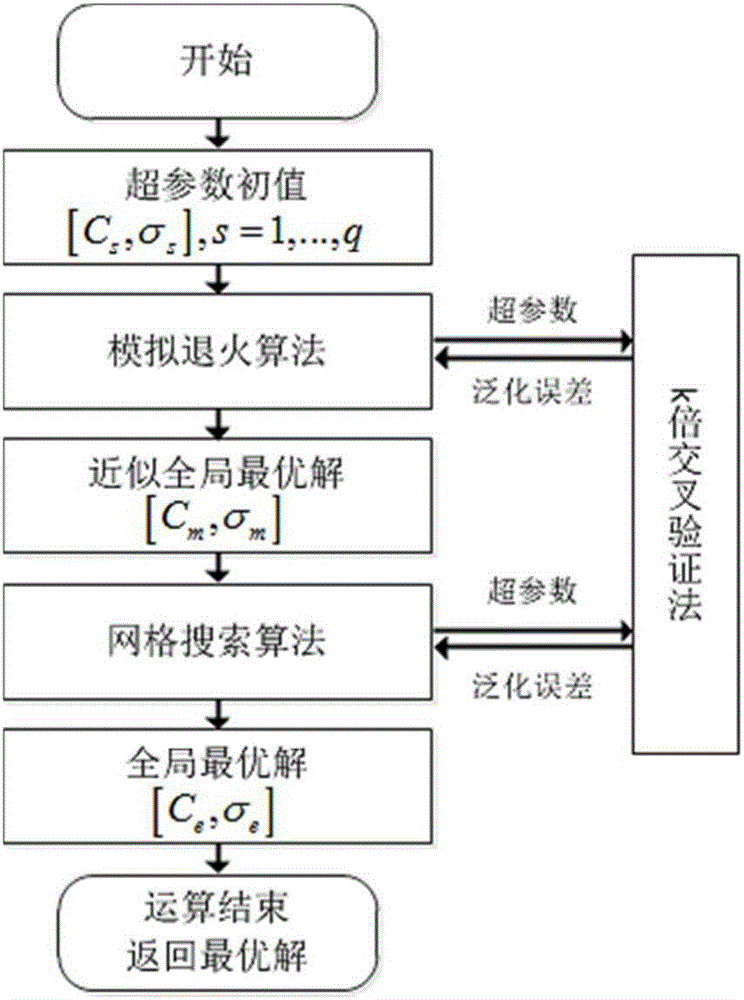
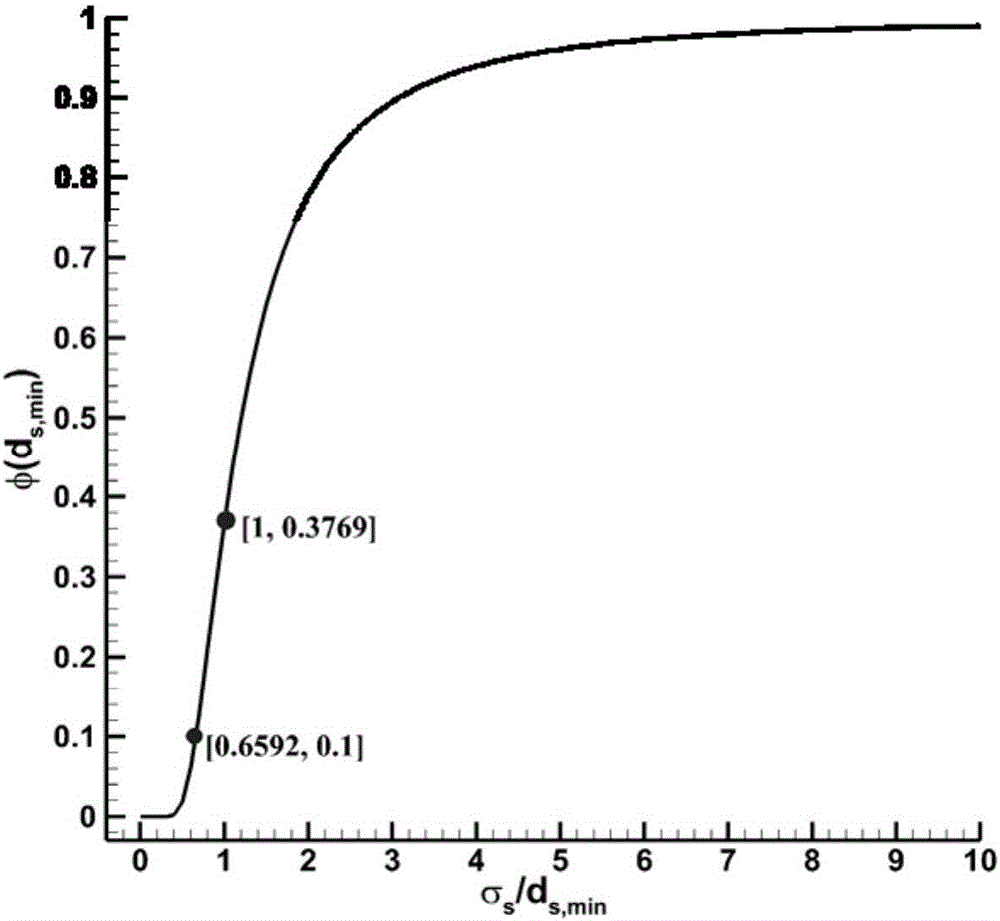
Support vector machine based automatic focusing method of ultrasonic phased arrays of ring welds
ActiveCN106841390AIntelligent Girth Weld Defect DetectionImprove detection accuracyAnalysing solids using sonic/ultrasonic/infrasonic wavesGeneralization errorSonification
The invention discloses a support vector machine based automatic focusing method of ultrasonic phased arrays of ring welds. The method includes: establishing a rectangular coordinate system, taking a least squares support vector regression (LSSVR) machine as the regression model and Gaussian radial basis function as the kernel function, performing training with input and output which are subjected to standardized processing, and establishing a prediction model of LSSVR initial function; taking a generalization error calculated with a k-fold cross validation method as the target function, optimizing the LSSVR initial function by adopting an optimization method combining a coupling-simulated annealing algorithm with a grid searching method to acquire an optimal hype-parameter and an LSSVR optimization model, predicting tested data to acquire the output, performing inverse normalization processing to obtain the optimal acoustic beam path plan of a corresponding partition, performing reverse solution according to the Fermat theorem to obtain time delay, and applying ultrasonic signals to perform focusing detection on ring weld defects. By the arrangement, the method has the advantages that intelligent ring weld defect detection is realized, and detection precision and efficiency are effectively improved.
Owner:ZHEJIANG UNIV
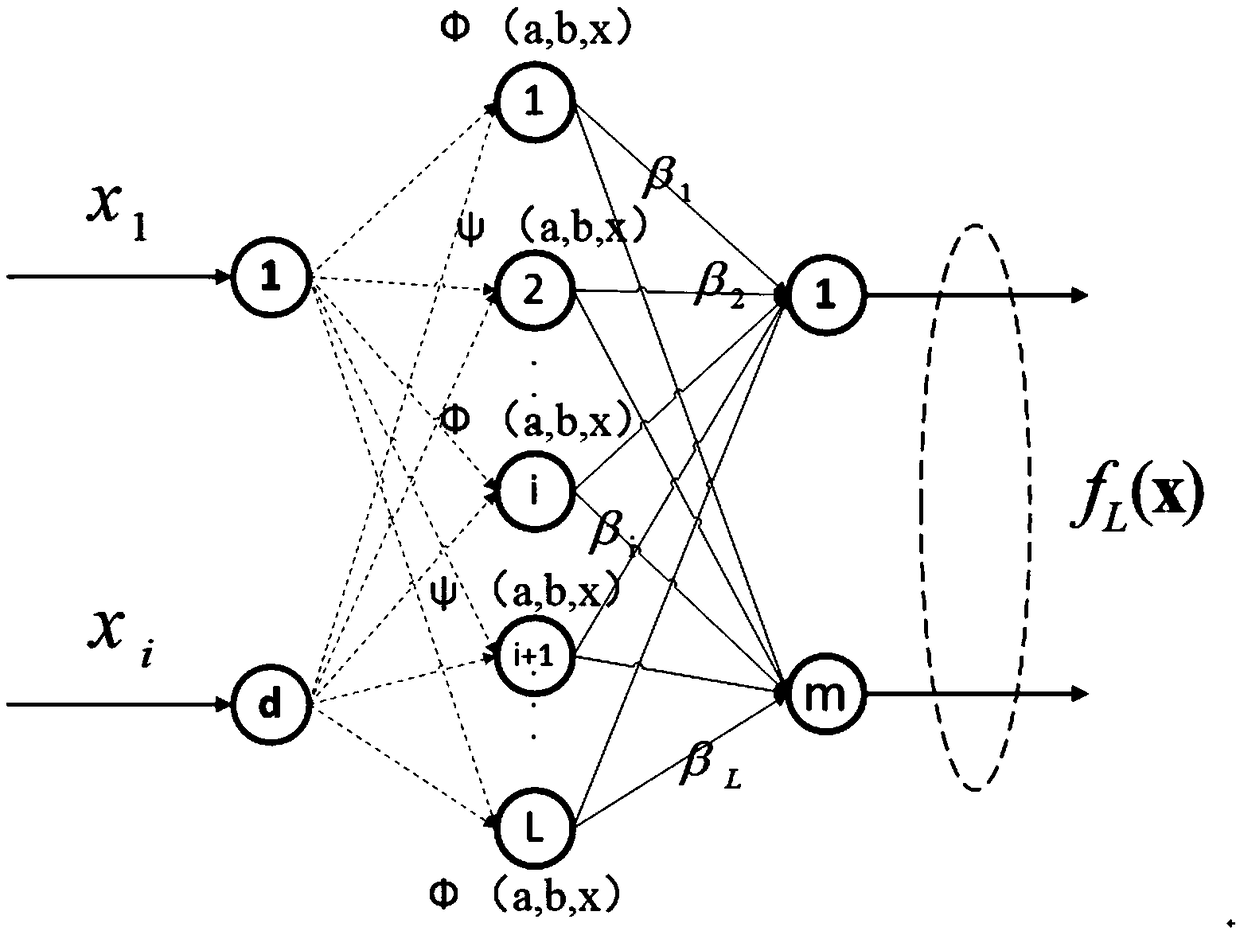
Parameter determining method of Gaussian radial basis function agent model
InactiveCN106295043AClear logicSimple and fast operationGeometric CADDesign optimisation/simulationGaussian radial basis functionInformation processing
The invention belongs to the field of information processing, and particularly relates to a parameter determining method of a Gaussian radial basis function agent model. According to the technical scheme, the parameter determining method includes the steps that sample space is linearly mapped into a unit cube; the local densities of sample points are calculated according to sample distribution conditions; the minimum distance between the sample point with the minimum local density and other sample points is calculated; the kernel widths of the sample points are determined; the weight coefficients of basis functions corresponding to the sample points are determined. The parameter determining method has the advantages that the method is clear in logic, easy and convenient to operate and easy to execute; the calculated amount is hardly increased with the basis-function kernel width determining method; the Gaussian radial basis function agent model obtained with the method can be commonly used for even / uneven samples, and the parameter determining method is reliable, efficient and high in accuracy.
Owner:NAT UNIV OF DEFENSE TECH
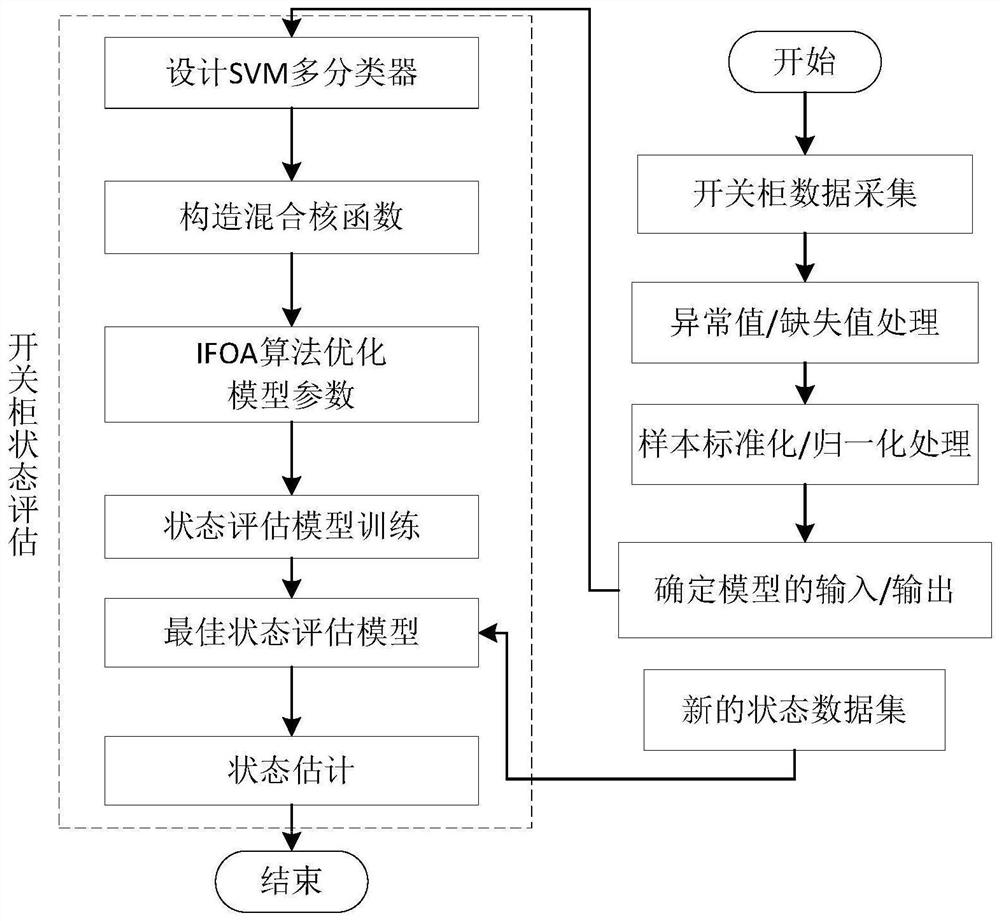
IFOA-SVM-based high-voltage switch cabinet state evaluation method
PendingCN113379251AImprove the shortcomings of easy to fall into local optimumGuaranteed convergenceCharacter and pattern recognitionArtificial lifeGaussian radial basis functionAlgorithm
The invention discloses an IFOA-SVM-based high-voltage switch cabinet state evaluation method. The method comprises the steps: firstly, collecting operation data of a high-voltage switch cabinet, and preprocessing the data through a method of deleting extreme abnormal values and complementing missing values; on the basis of a field investigation result and expert experience, selecting characteristic quantities for evaluating the high-voltage switch cabinet as a partial discharge value, an ultrasonic value, infrared diagnosis, a cable joint temperature and a busbar temperature; then, combining a polynomial function and a Gaussian radial basis function to construct a mixed kernel function, and mapping an original input space to a high-dimensional feature space; then optimizing a kernel function proportionality coefficient, a kernel function width parameter and a penalty factor by using an improved fruit fly optimization algorithm; and finally, by training an OVO-SVM high-voltage switch cabinet state estimation classifier, realizing nonlinear classification of the high-voltage switch cabinet state, namely, high-voltage switch cabinet state evaluation. According to the invention, multi-source information is utilized to carry out state comprehensive evaluation on the distribution high-voltage switch cabinet, a theoretical framework is simple, and the method is easy to implement and high in generalization ability.
Owner:ZHEJIANG UNIV OF TECH
Support vector machine-based cabin interior path loss prediction method
InactiveCN102651071BImprove accuracyVerify validityPower managementSupport vector machineGaussian radial basis function
Owner:TIANJIN UNIV
A method for analyzing the relationship between the cause of performance failure and characteristic parameters of a communication network
InactiveCN109088754AHigh precisionImprove generalization abilityData switching networksLearning machineGaussian radial basis function
The invention discloses a communication network performance fault cause and characteristic parameter correlation analysis method, and relates to the technical field of communication network fault diagnosis. The method obtains the characteristic parameter data of the communication network performance fault to be analyzed, adopts a communication network performance fault analysis model of a transfinite learning machine established in advance, and processes the characteristic parameter of the communication network performance fault to be analyzed, thereby analyzing the communication network performance fault types corresponding to the characteristic parameter. The invention realizes the effective and accurate analysis of the communication network performance fault types, and enhances the generalization ability of the traditional transfinite learning machine model and improves the model precision by selecting two different activation functions, the sigmoid activation function and the Gaussian radial basis function.
Owner:BEIHANG UNIV
Oil and gas reservoir parameter interpretation method and device based on neural network and electronic equipment
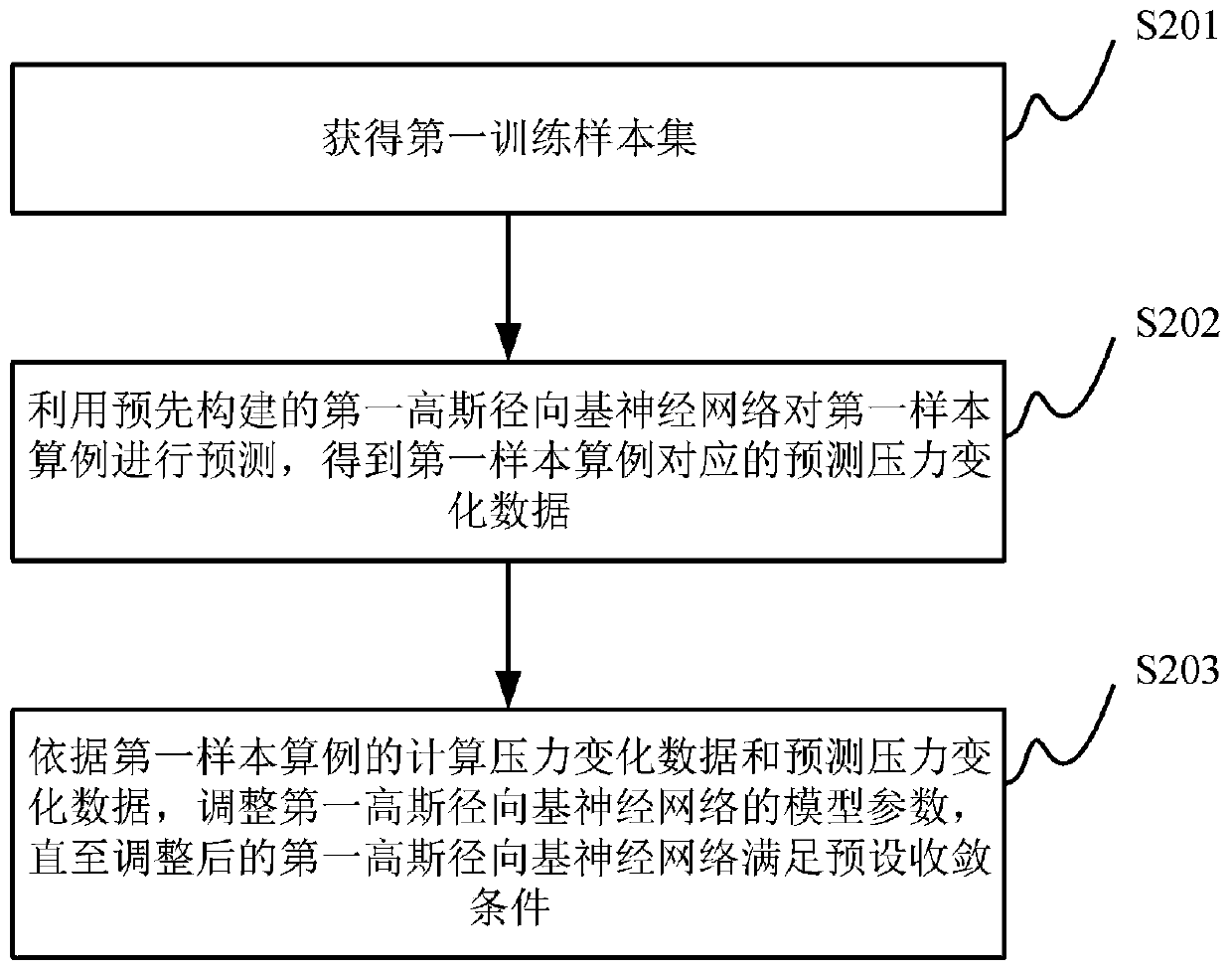
ActiveCN110991079AReduce workloadAccurate predictionClimate change adaptationDesign optimisation/simulationGaussian radial basis functionNumerical range
The invention discloses an oil and gas reservoir parameter interpretation method and device based on a neural network and electronic equipment. The method comprises the steps of receiving to-be-interpreted parameter and a corresponding numerical range; sampling the to-be-interpreted parameter in the numerical range to obtain a trial calculation example; respectively inputting the trial calculationexample into a first Gaussian radial basis function neural network and a second Gaussian radial basis function neural network to obtain corresponding calculation pressure change data and calculationpressure derivative data; and calculating a target function value, if the target function value is smaller than or equal to judgment threshold, taking the parameter value contained in the current trial example as an interpretation result of the to-be-interpreted parameter, and if the target function value is greater than the judgment threshold, executing the step of sampling in the numerical rangeand the subsequent steps again until the interpretation result of the to-be-interpreted parameter is obtained. Based on the scheme provided by the invention, the efficiency and precision of numericalwell test interpretation can be improved, and the working intensity of well test interpretation personnel is reduced.
Owner:合肥鼎盛锦业科技有限公司
Prediction method of performance index of drawing link in the production process of carbon fiber precursor
InactiveCN106446495BAchieving Precise ForecastingImprove forecast accuracyForecastingInformaticsFiberData set
The invention relates to a method for predicting performance indexes of a drafting link in a carbon fiber precursor production process, in particular to a method for predicting performance indexes of a drafting link in a carbon fiber precursor production process based on a least square support vector machine (LS-SVM) optimized by a particle swarm optimization (PSO) algorithm improved by a power law. The method comprises the following steps of selecting a six-stage draft ratio of the drafting link in the carbon fiber precursor production process as feature information, performing linear function normalization, and establishing an input sample dataset; determining main performance indexes, including linear density, precursor strength and breaking elongation rate, influencing carbon fiber quality, performing logarithmic function normalization, and establishing an output sample dataset; and building an LS-SVM model according to the input and output sample datasets, adopting a Gauss radial basis function (RBF) as a kernel function of the LS-SVM, and selecting an optimal penalty factor C and a kernel function parameter sigma by using PSO. The PSO process is improved according to the power law, so that the optimization speed can be greatly increased and accurate prediction is realized.
Owner:DONGHUA UNIV
A Design Method of Imaging System Based on Gaussian Radial Basis Function Surface
ActiveCN113126289BSimple methodEasy to implementCharacter and pattern recognitionOptical elementsGaussian radial basis functionGaussian function
The invention discloses an imaging system design method based on Gaussian radial basis function curved surface. The present invention takes the optical system whose field of view is smaller than the required value as the design starting point, and then gradually increases the field of view. Based on the idea of "expanding the field of view, Gaussian continuation", new Gaussian functions are sequentially added to the curved surface with the expansion of the field of view Edge, gradually expand the size of the surface, through progressive optimization to obtain an imaging system that finally meets the design indicators. The method of the invention is simple and easy to implement, and is especially suitable for the design of a large field of view imaging optical system. The invention provides convenience for the actual imaging system to use the Gaussian radial basis function surface, and is convenient and convenient, and has strong applicability. This method can be used for various applications and free-form surface imaging systems of various system structures, from a simple system As a starting point, gradually complete the system design.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
Low-dimensional nano material identification method based on SEM image
ActiveCN102183535BAccurately reflectSmall amount of calculationCharacter and pattern recognitionNanotechnologySupport vector machineGaussian radial basis function
The invention belongs to the crossed technical field of computer mode identification and nano material, and relates to a low-dimensional nano material identification method based on an SEM image. The method comprises the following steps of: (1) preprocessing a known nano material SEM image sample; (2) performing two-dimensional wavelet transformation on the preprocessed image to get sub-image matrixes on different frequency bands; (3) extracting characteristics of the sub-image matrixes on each frequency band, and taking a statistical value of each sub-image matrix as a characteristic value for representing surface texture of the nano material; (4) according to the characteristic value, taking a Gaussian radial basis function as a support vector machine kernel function to find an optimal hyperplane between any two classes, and creating a classification model for different classes of nano materials; (5) extracting a texture characteristic value of the known nano material SEM image sample, and identifying the unknown nano material by voting according to the classification model obtained in the step (4). The low-dimensional nano material identification method based on the SEM image represents and distinguishes different nano material structure types more accurately and effectively, and has the advantages of high accuracy, strong expansibility, high degree of automation and the like.
Owner:NANTONG HUALONG MICROELECTRONICS
Construction method and prediction method of woody plant leaf phenotypic characteristics and photosynthetic characteristics prediction model based on DNA methylation level
InactiveCN108319984BBiostatisticsCharacter and pattern recognitionDNA methylationGaussian radial basis function
The invention provides a construction method and a prediction method of a woody plant leaf trait and photosynthetic characteristic model based on the DNA methylation level, and belongs to the technical field of biological analysis. The present invention selects important characteristic variables that reflect geographical location differences based on random forests, obtains seven leaf characteristic variables by screening, determines the optimal number of clusters, and uses the improved FCM clustering algorithm to obtain each group of clustered leaf samples; according to the correlation between variables The importance of the enzyme cut combination obtained from the gradient boosting tree is used to obtain the important enzyme cut combination in each group of clustered leaf samples; the DNA methylation level of the enzyme cut combination is used as a regression variable, and the LS is constructed based on the Gaussian radial basis function ‑SVM regression prediction model; input DNA methylation levels of important enzyme cleavage combinations to accurately predict leaf shape factor, leaf area and net photosynthetic rate. The method is used to predict the phenotypic characteristics and photosynthetic characteristics of woody plants, and simultaneously screen woody plant individuals with excellent traits.
Owner:BEIJING FORESTRY UNIVERSITY
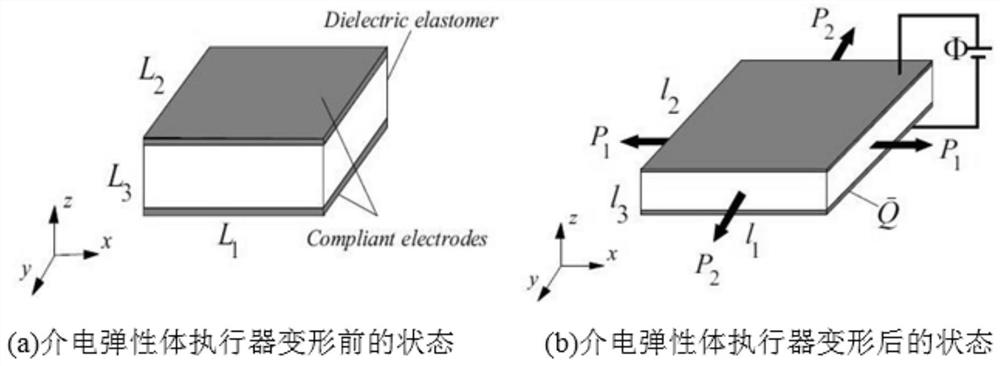
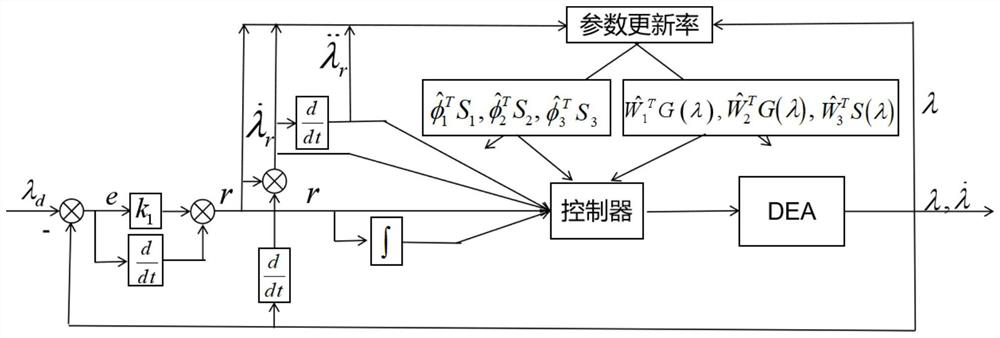
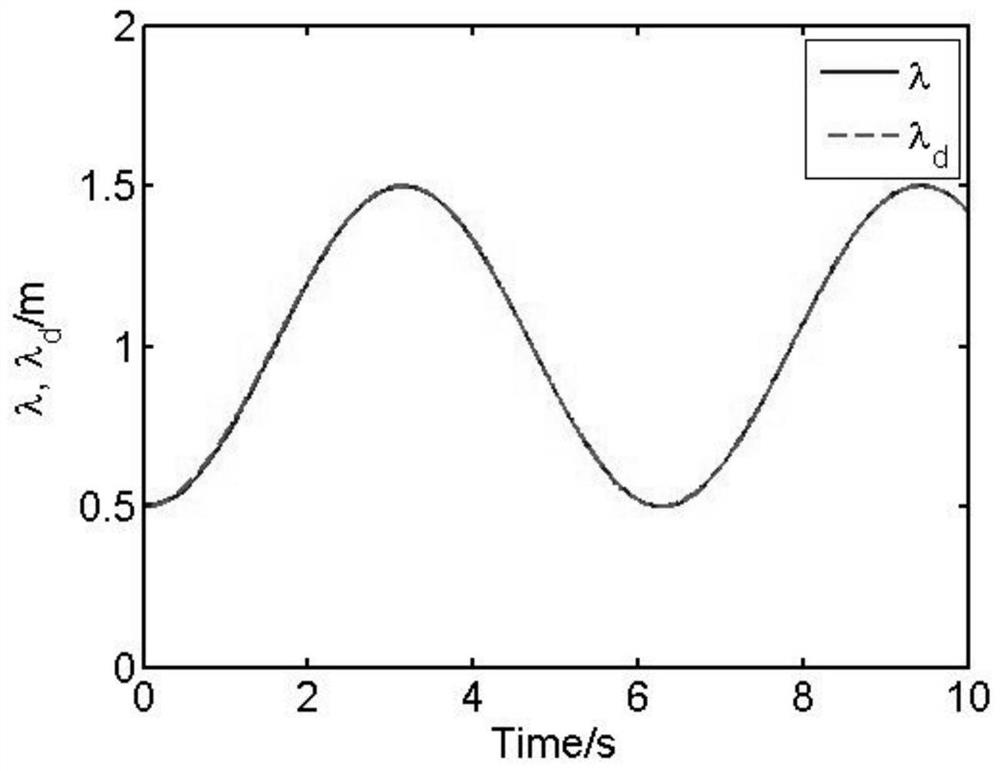
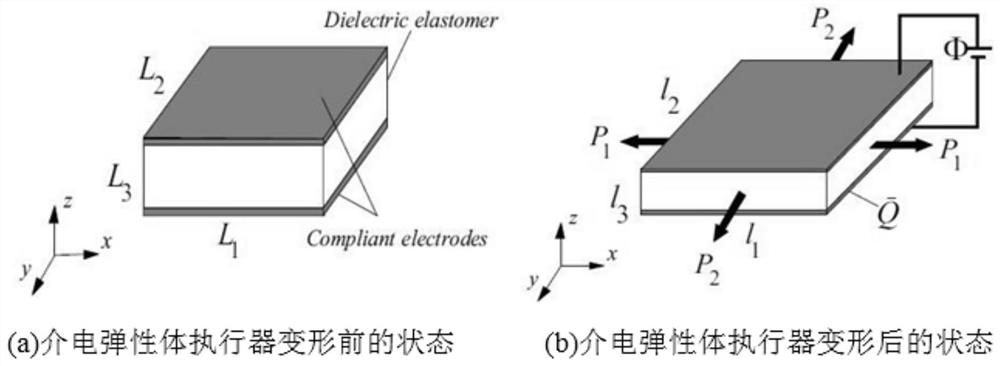
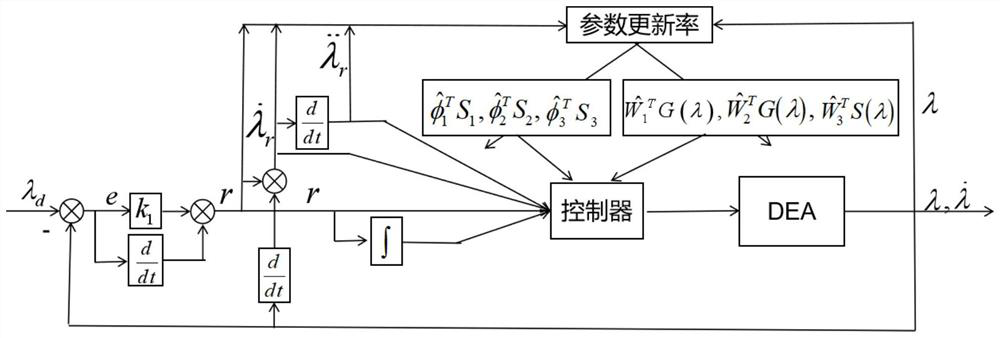
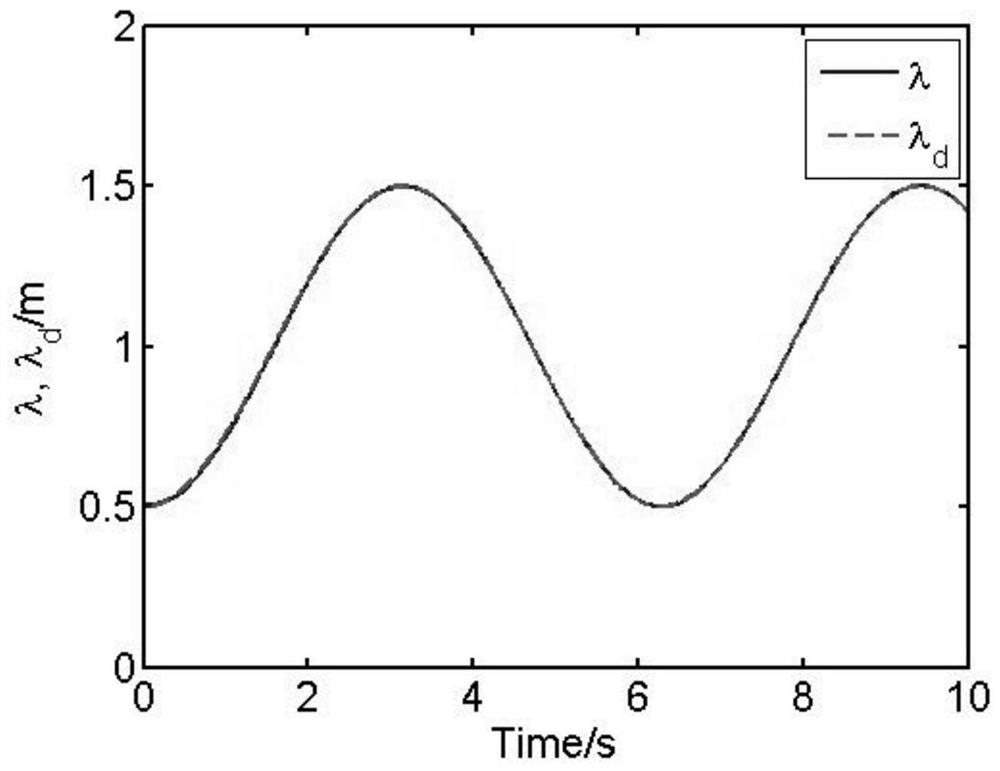
Soft robot state feedback control method based on dielectric elastomer actuator
ActiveCN112589798AAchieve control objectivesImprove adaptability and intelligenceProgramme-controlled manipulatorSimulationDielectric elastomer actuator
The invention discloses a soft robot state feedback control method based on a dielectric elastomer actuator. The method comprises the steps of building a dynamic control model of the dielectric elastomer actuator in a mode of virtual work simulation; building a Gaussian radial basis function neural network approximator for an unknown system function in the dynamic control model; by correspondinglydesigning a parameter updating rate, dynamically adjusting the parameters of the Gaussian radial basis function neural network approximator on line to realize the on-line approximation of the unknownsystem function; and finally, building a state feedback intelligent controller embedded with the Gaussian radial basis function neural network approximator in a state feedback control mode for dynamically adjusting the control input of the dielectric elastomer actuator on line in order to enable a state tracking error to converge to zero to realize a control target of a soft robot. According to the method, the control precision and the response speed of a control system are enhanced, and the adaptability and the intelligence of the soft robot based on the dielectric elastomer actuator are improved.
Owner:CHONGQING UNIV OF TECH
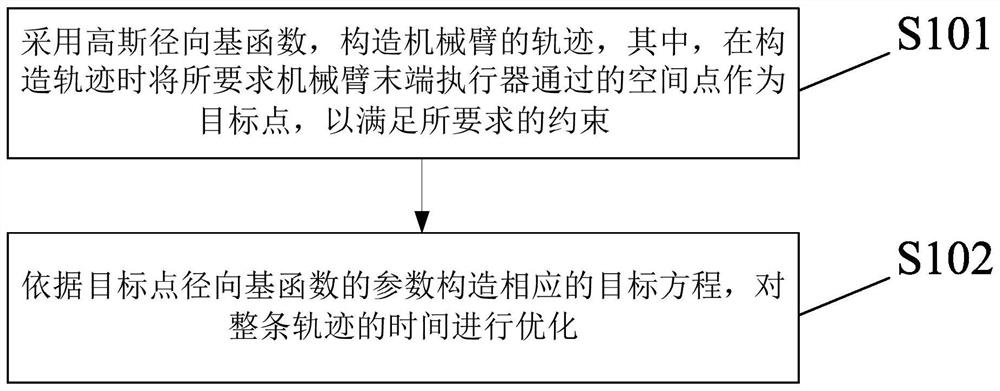
Mechanical arm point-to-point trajectory planning method and device based on radial basis function
ActiveCN112975986AGuaranteed performanceOptimize accelerationProgramme-controlled manipulatorGaussian radial basis functionClassical mechanics
The embodiment of the invention provides a mechanical arm point-to-point trajectory planning method based on a radial basis function. The method comprises the steps of constructing a motion trajectory of a mechanical arm by adopting a Gaussian radial basis function; and constructing a corresponding optimization target equation according to parameters of the radial basis function, and optimizing the time of the whole trajectory. According to the method of the invention, the smooth motion trajectory can be generated between any target points, and any order derivative of the trajectory is continuous and is not influenced by the number of the target points. Meanwhile, the generated trajectory is simple in form and small in calculated amount, important parameters such as acceleration and jerk of the trajectory can be optimized through unified parameters, the smoothness of the trajectory is improved, then the running time of the whole trajectory is shortened, and the smoothness and working efficiency of the mechanical arm are improved.
Owner:珞石(北京)科技有限公司
Representation Method of Optical Freeform Surface Based on Gaussian Radial Basis Function
ActiveCN112130318BSimple calculationStrong face shape adaptabilityOptical elementsGaussian radial basis functionEngineering
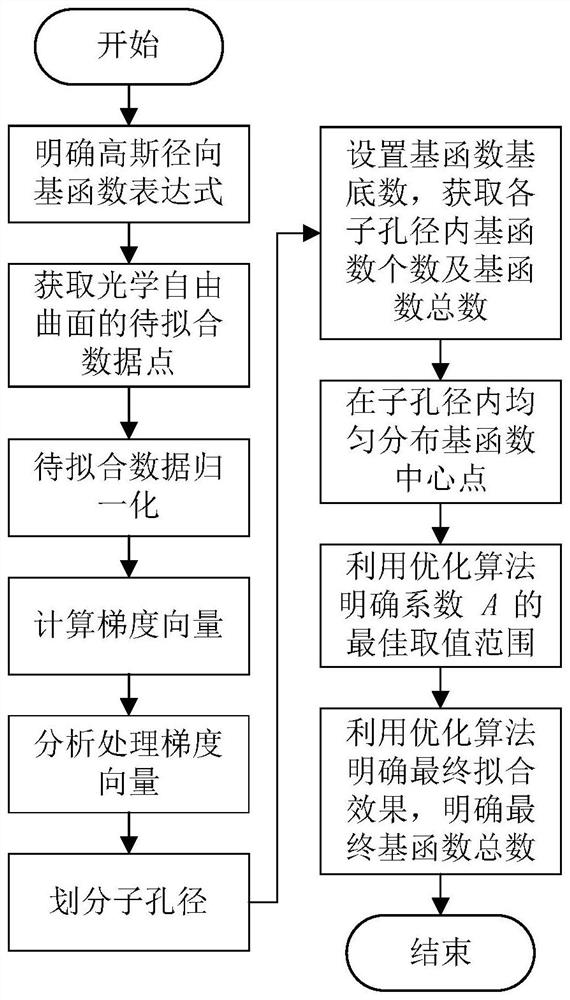
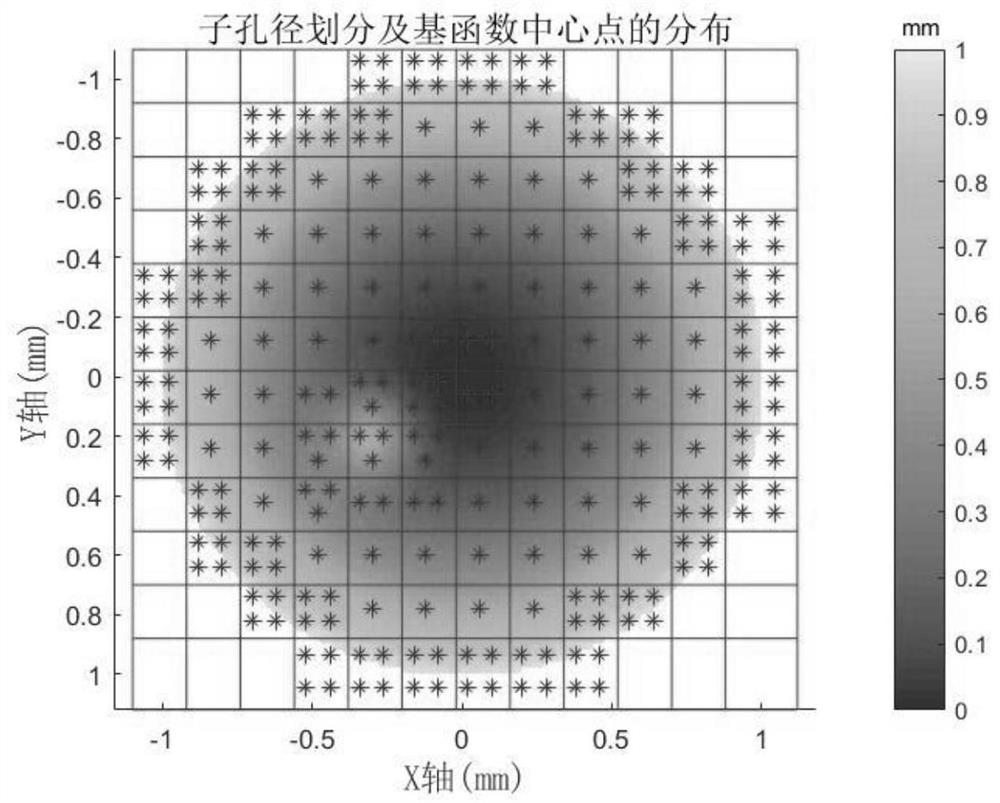
A characterization method for optical free-form surfaces based on Gaussian radial basis functions is disclosed, by clarifying the expression of Gaussian radial basis functions, obtaining the data point set to be fitted to the optical free-form surface to be fitted, and normalizing the data to be fitted , Calculate the gradient vector according to the normalized data to be fitted, analyze and process the gradient vector, divide the sub-aperture, set the number of Gaussian radial basis function bases, obtain the number of Gaussian radial basis functions in each sub-aperture, and obtain the Gaussian radial basis function The total number of basis functions, the center point of the Gaussian radial basis function uniformly distributed in the sub-aperture, the optimal value range of the coefficient A, the final fitting effect, and the final total number of basis functions are specified, so that complex optical free-form surfaces can be processed High-precision characterization can meet the needs of modern optical system design, processing and testing. This method is simple to calculate, easy to implement, and has strong surface shape adaptability. It is suitable for any caliber and can realize high-precision characterization of optical free-form surfaces.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
A State Feedback Control Method for Soft Robots Based on Dielectric Elastomeric Actuators
ActiveCN112589798BImprove adaptabilityImprove intelligenceProgramme-controlled manipulatorControl mannerSimulation
The invention discloses a state feedback control method of a soft robot based on a dielectric elastic body actuator, which uses virtual work simulation to establish a dynamic control model of a dielectric elastic body actuator, and then controls the unknown system function in the dynamic control model Constructing a Gaussian radial basis function neural network approximator, and by correspondingly designing its parameter update rate, the parameters of the Gaussian radial basis function neural network approximator are dynamically adjusted online to realize the online approximation to the unknown system function, Finally, a state feedback intelligent controller embedded with the Gaussian radial basis function neural network approximator is constructed in a state feedback control mode, which is used to dynamically adjust the control input of the dielectric elastomer actuator online so that the state tracking error converges to zero , so as to achieve the control goal of soft robots, to enhance the control accuracy and response speed of the control system, and to improve the adaptability and intelligence of soft robots based on dielectric elastomer actuators.
Owner:CHONGQING UNIV OF TECH
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com