Eureka AIR delivers breakthrough ideas for toughest innovation challenges, trusted by R&D personnel around the world.

A Design Method of Imaging System Based on Gaussian Radial Basis Function Surface

A Gaussian radial basis and imaging system technology, applied in computing, computer components, instruments, etc., can solve the problems of not fully utilizing the local properties of Gaussian functions, and achieve the effect of easy implementation and simple method

Active Publication Date: 2022-02-11
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, there are few existing methods for designing imaging optical systems using Gaussian functions. Unchanged, did not make full use of the local properties of the Gaussian function, not suitable for system design with higher system parameters (such as large field of view) starting from a system with lower system parameters

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Design Method of Imaging System Based on Gaussian Radial Basis Function Surface
  • A Design Method of Imaging System Based on Gaussian Radial Basis Function Surface
  • A Design Method of Imaging System Based on Gaussian Radial Basis Function Surface

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0022] The present invention will be described in detail below with reference to the accompanying drawings and examples.

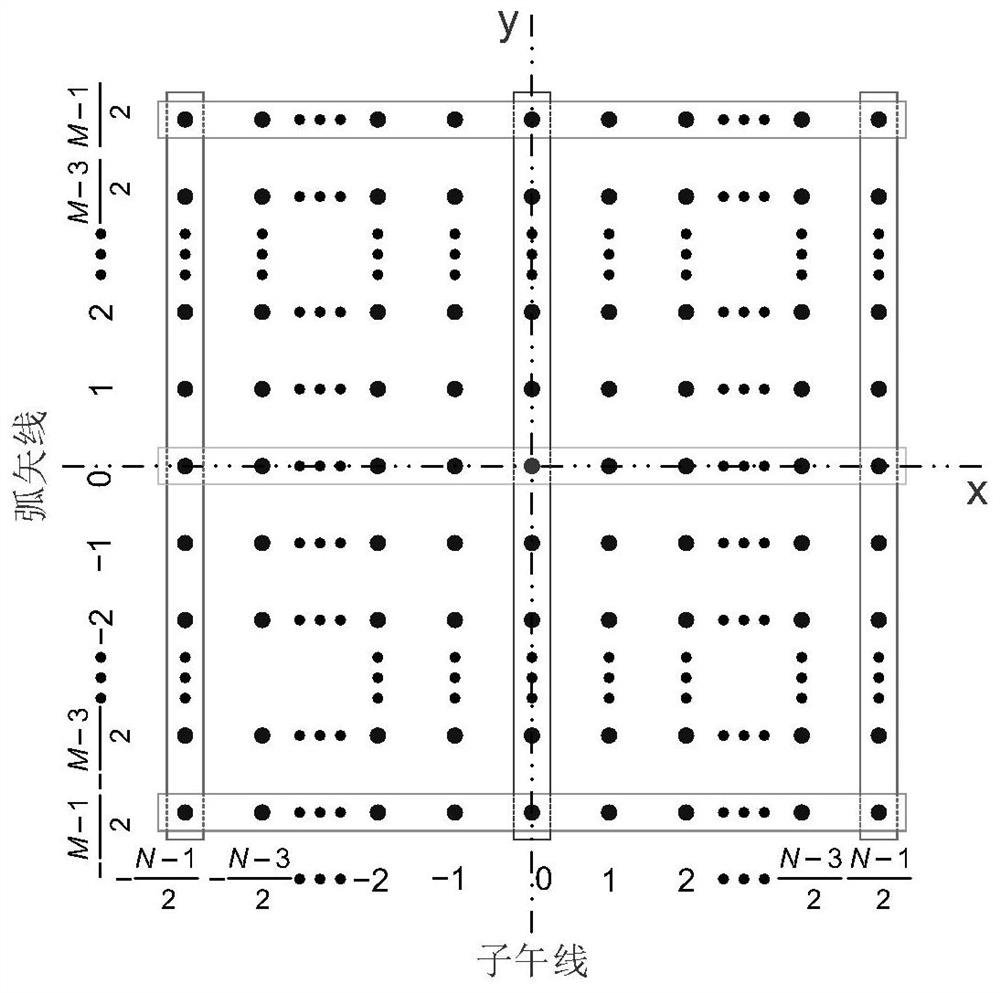
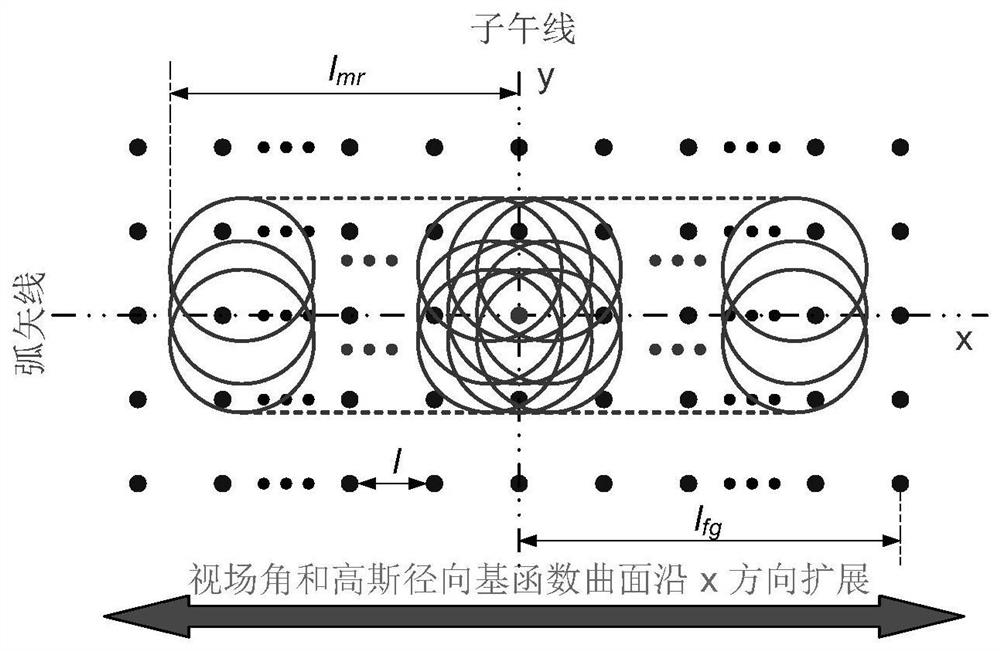
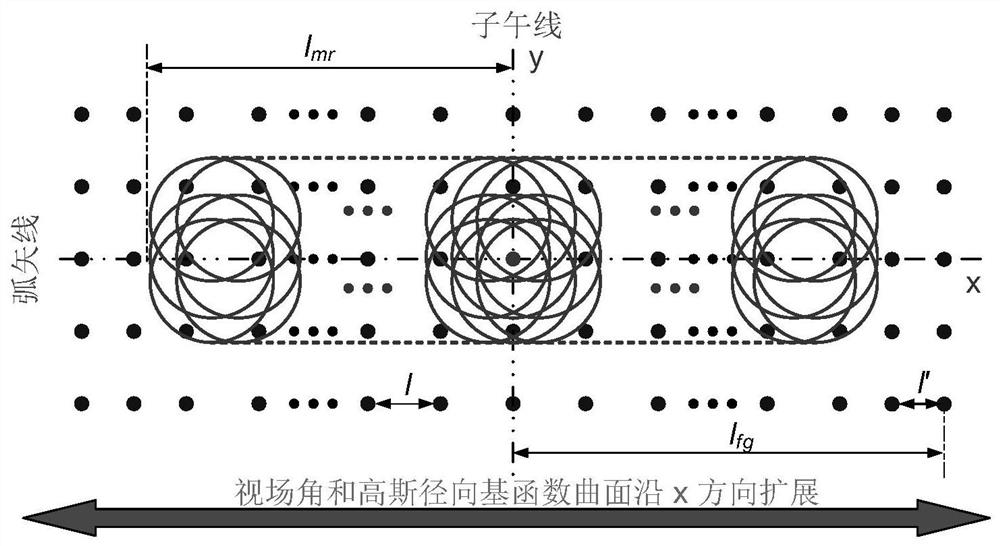
[0023] The invention provides an imaging system design method based on Gaussian radial basis function surface.

[0024] As a radial basis, the Gaussian function has locality, and has the ability to control the local surface shape in the surface shape description. The mathematical expression of a typical standard two-dimensional Gaussian function can be defined by the standard deviation σ and the center position (x i ,y i ) to describe, namely:

[0025]

[0026] A Gaussian radial basis function surface for an imaging system consists of the sum of the base quadric and a set of weighted Gaussian terms:

[0027]

[0028] In the formula, c is the curvature at the vertex of the surface, k is the coefficient of the quadratic surface, and g j (x,y)(1≤j≤J) is the same standard deviation but the center position (x i ,y i ) different Gaussian functions, w...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an imaging system design method based on Gaussian radial basis function curved surface. The present invention takes the optical system whose field of view is smaller than the required value as the design starting point, and then gradually increases the field of view. Based on the idea of ​​"expanding the field of view, Gaussian continuation", new Gaussian functions are sequentially added to the curved surface with the expansion of the field of view Edge, gradually expand the size of the surface, through progressive optimization to obtain an imaging system that finally meets the design indicators. The method of the invention is simple and easy to implement, and is especially suitable for the design of a large field of view imaging optical system. The invention provides convenience for the actual imaging system to use the Gaussian radial basis function surface, and is convenient and convenient, and has strong applicability. This method can be used for various applications and free-form surface imaging systems of various system structures, from a simple system As a starting point, gradually complete the system design.

Description

technical field [0001] The invention relates to the technical field of optical design, in particular to an imaging system design method based on a Gaussian radial basis function surface. Background technique [0002] Compared with traditional spherical or aspheric surfaces, free-form surfaces can provide more degrees of freedom in optical design, which can greatly improve the imaging quality of the system, and make the system structure more flexible, with fewer components, smaller volume, and lighter weight. Therefore, freeform surfaces are considered a revolutionary development in the field of optical design. The curved surface based on Gaussian function is a kind of free-form surface, which has some excellent properties in optical design. First, Gaussian functions are smooth and continuous, with derivatives of arbitrary order. This feature facilitates ray tracing. Secondly, the Fourier transform of the Gaussian function is itself, which is of great significance in the c...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G02B27/00G06K9/62G06V10/764
CPCG02B27/0012G06F18/2414
Inventor 杨通倪俊豪程德文王涌天
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com