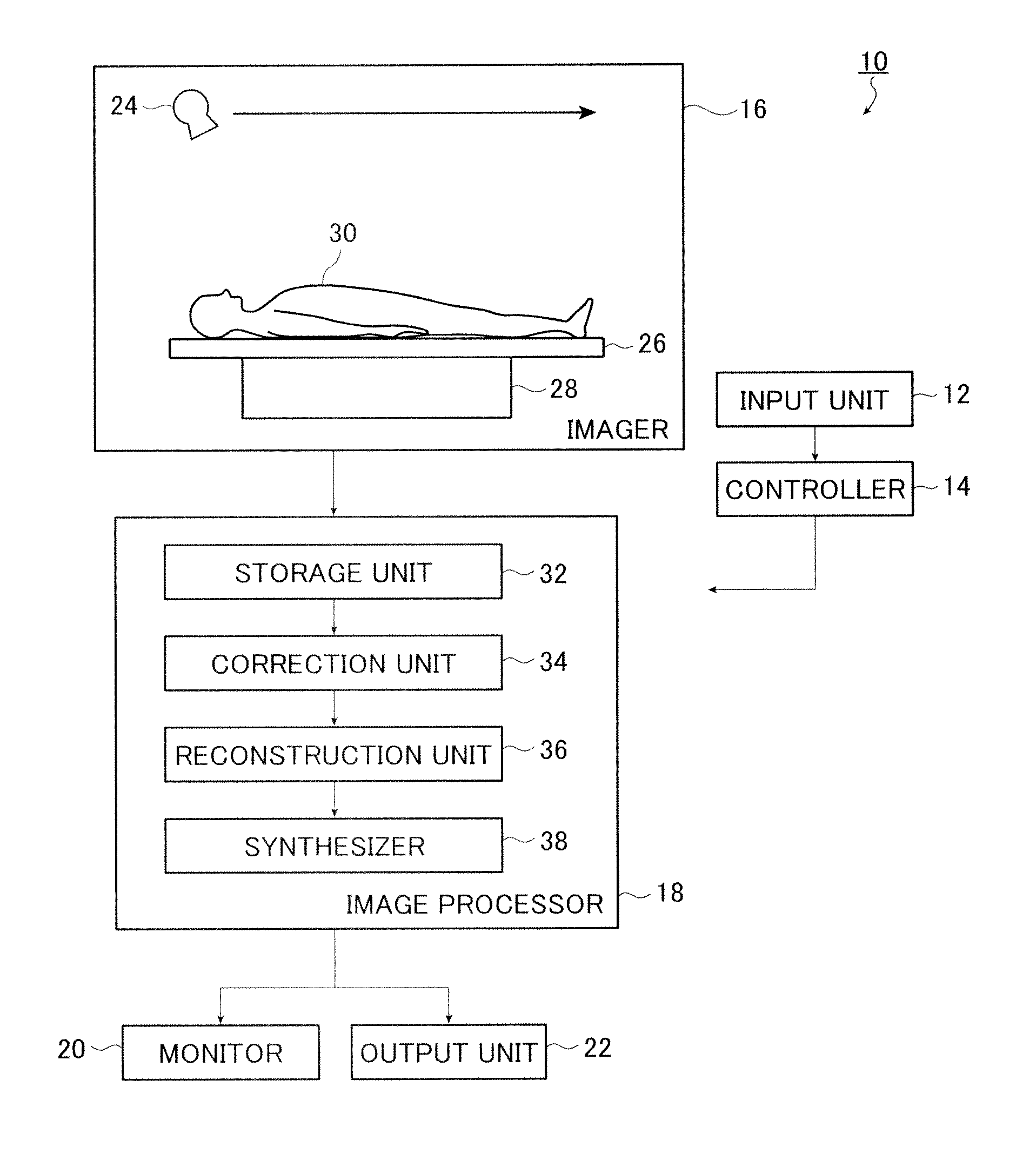
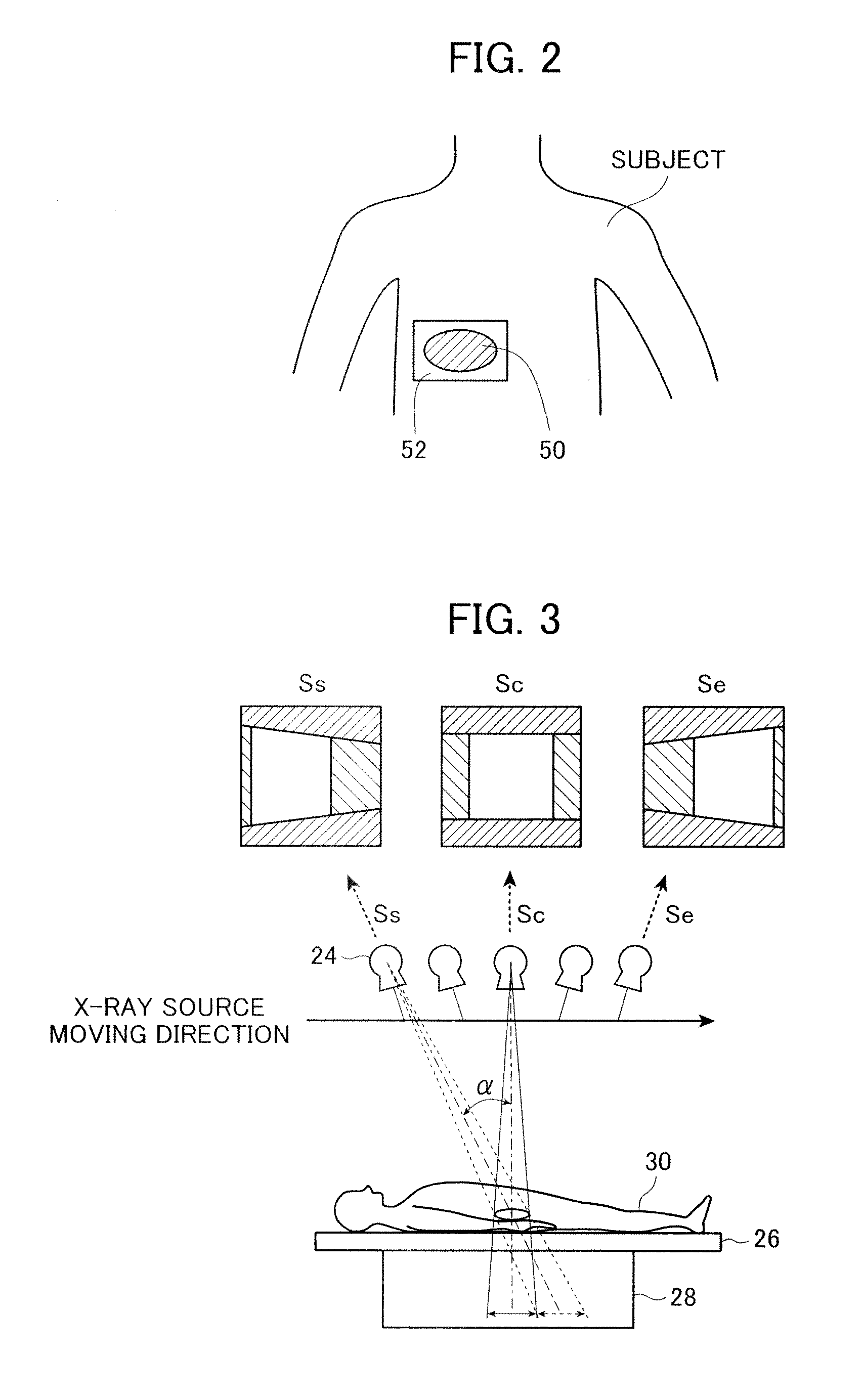
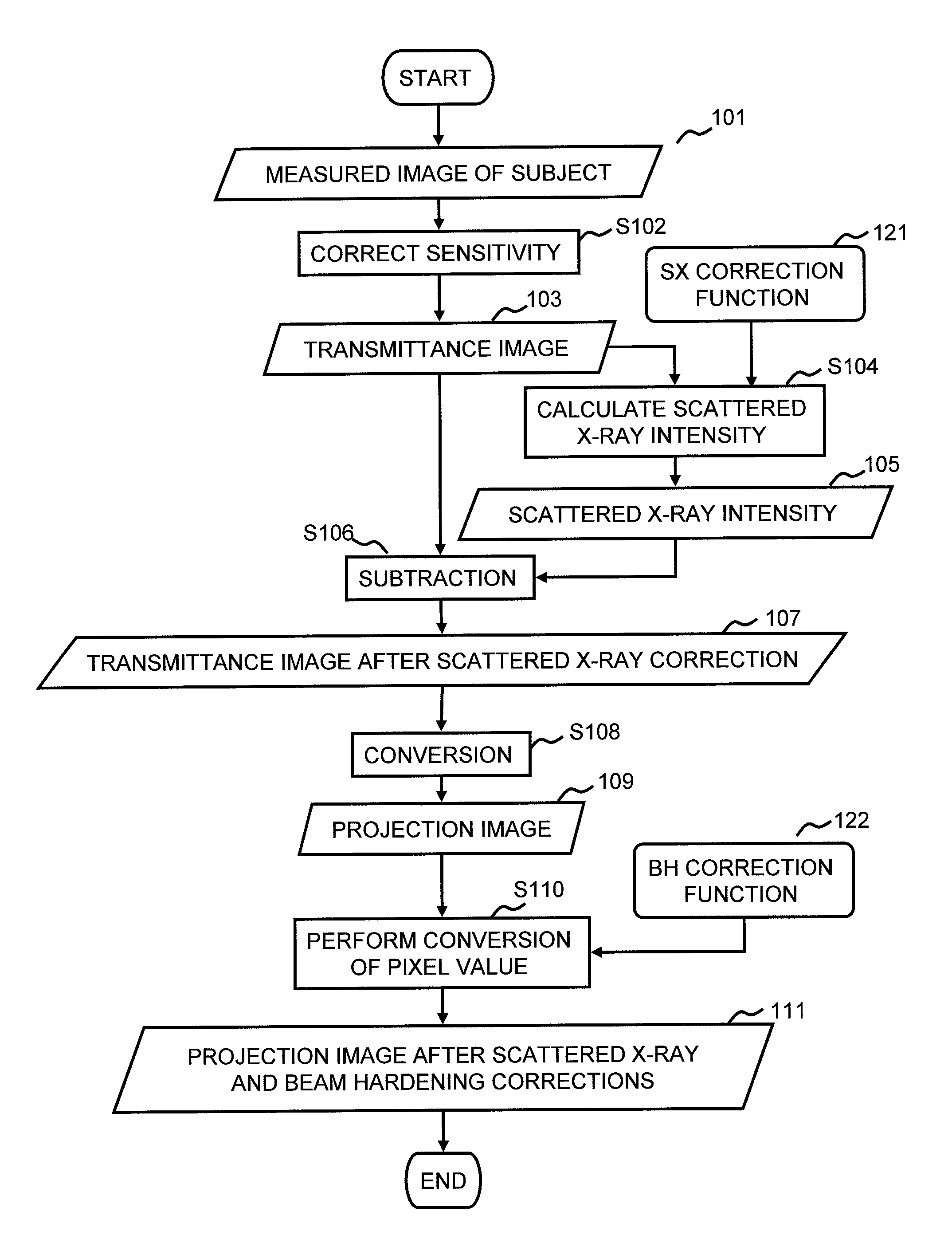
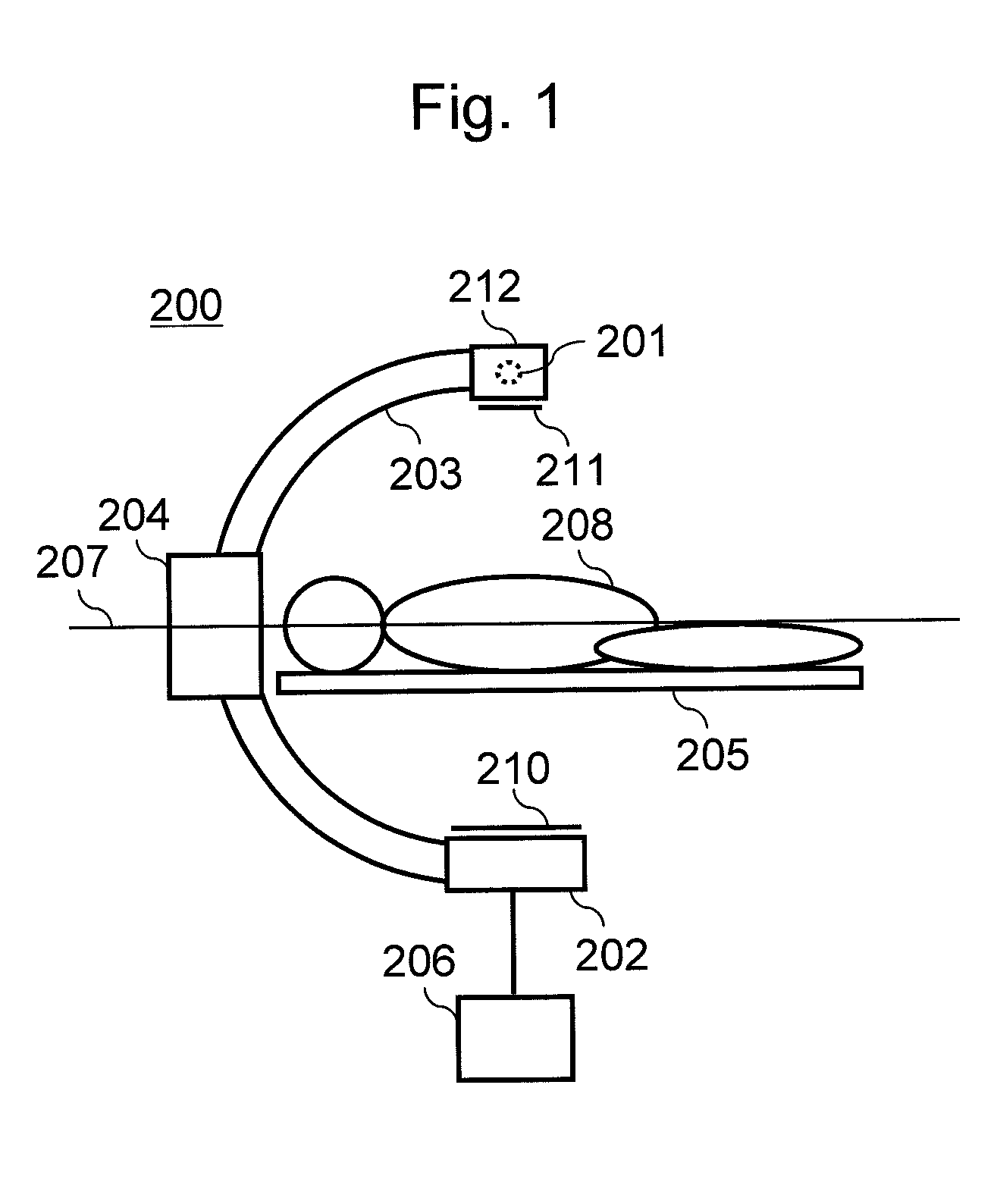
Patents
Literature
Hiro is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
7154results about "Reconstruction from projection" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
Augmented surgical reality environment
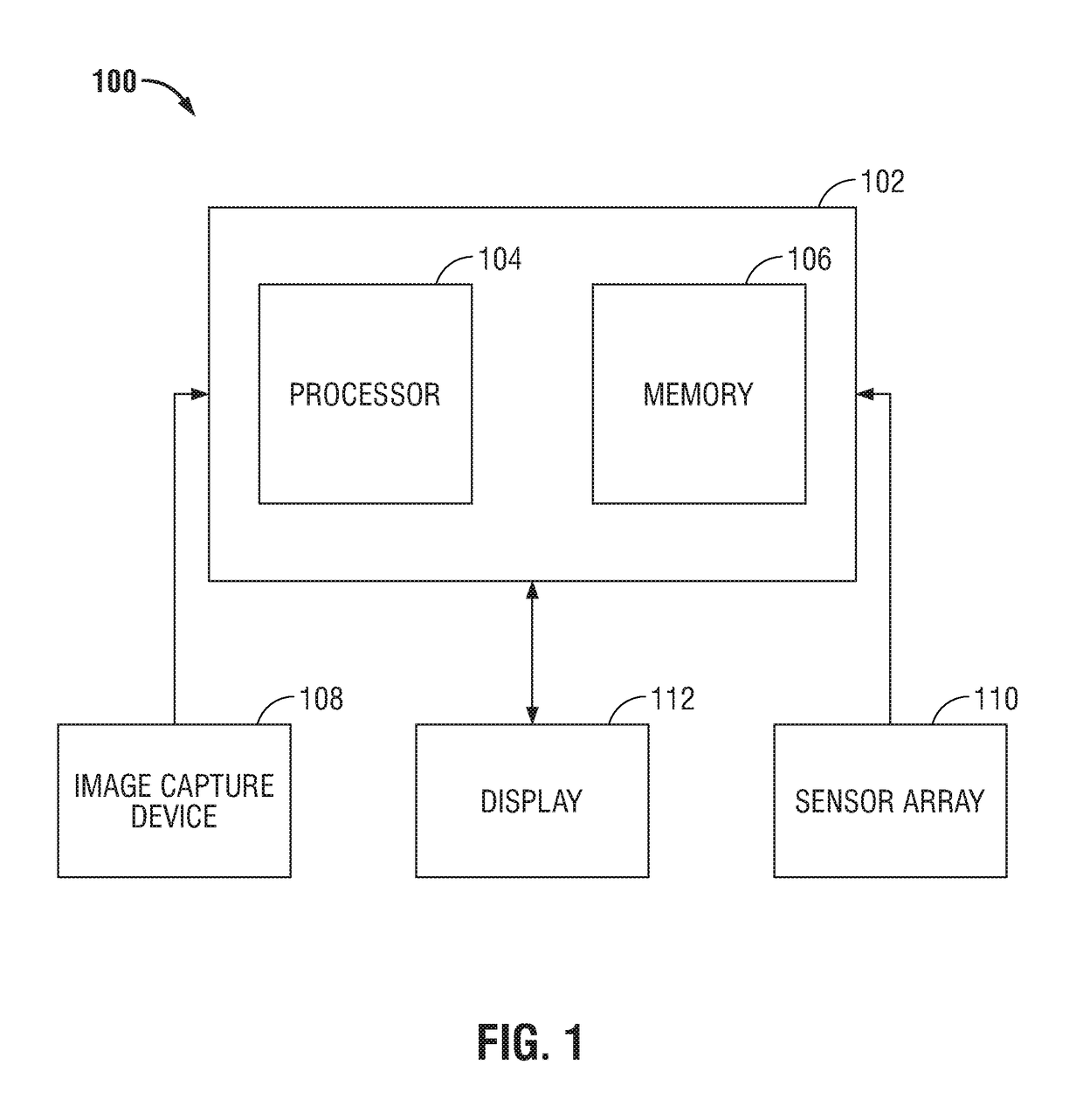
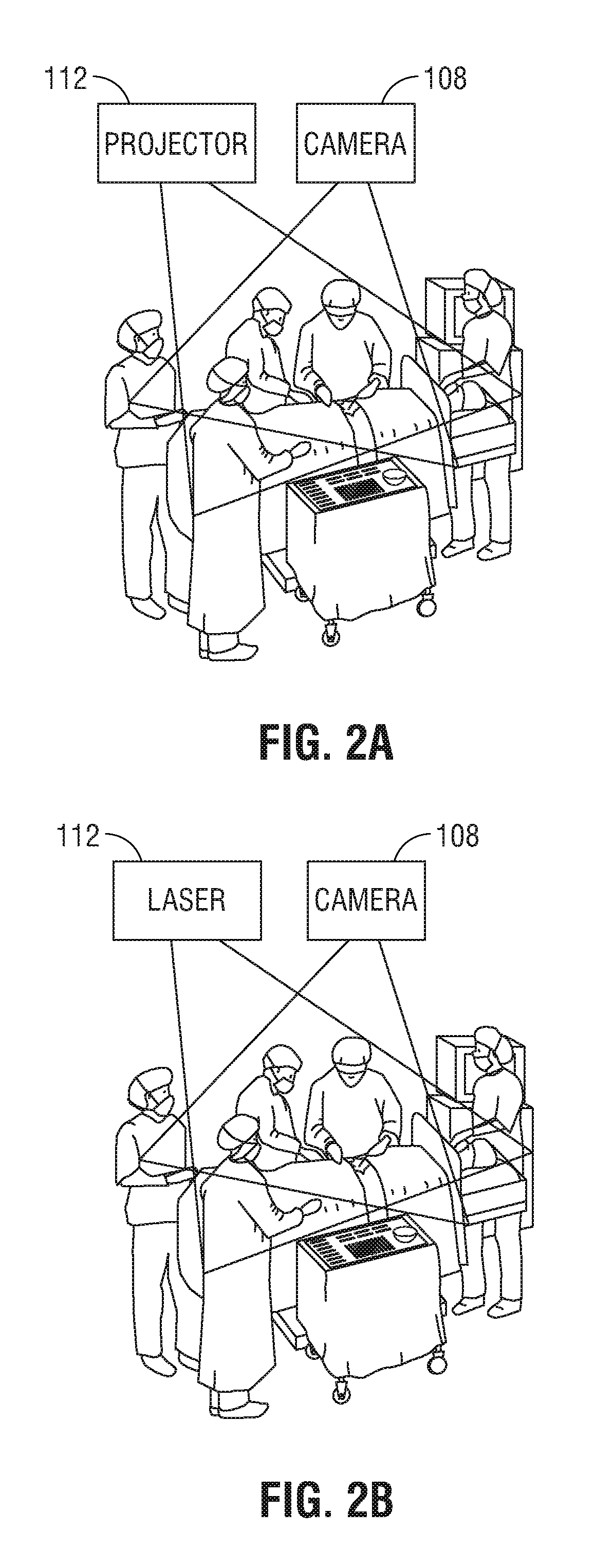
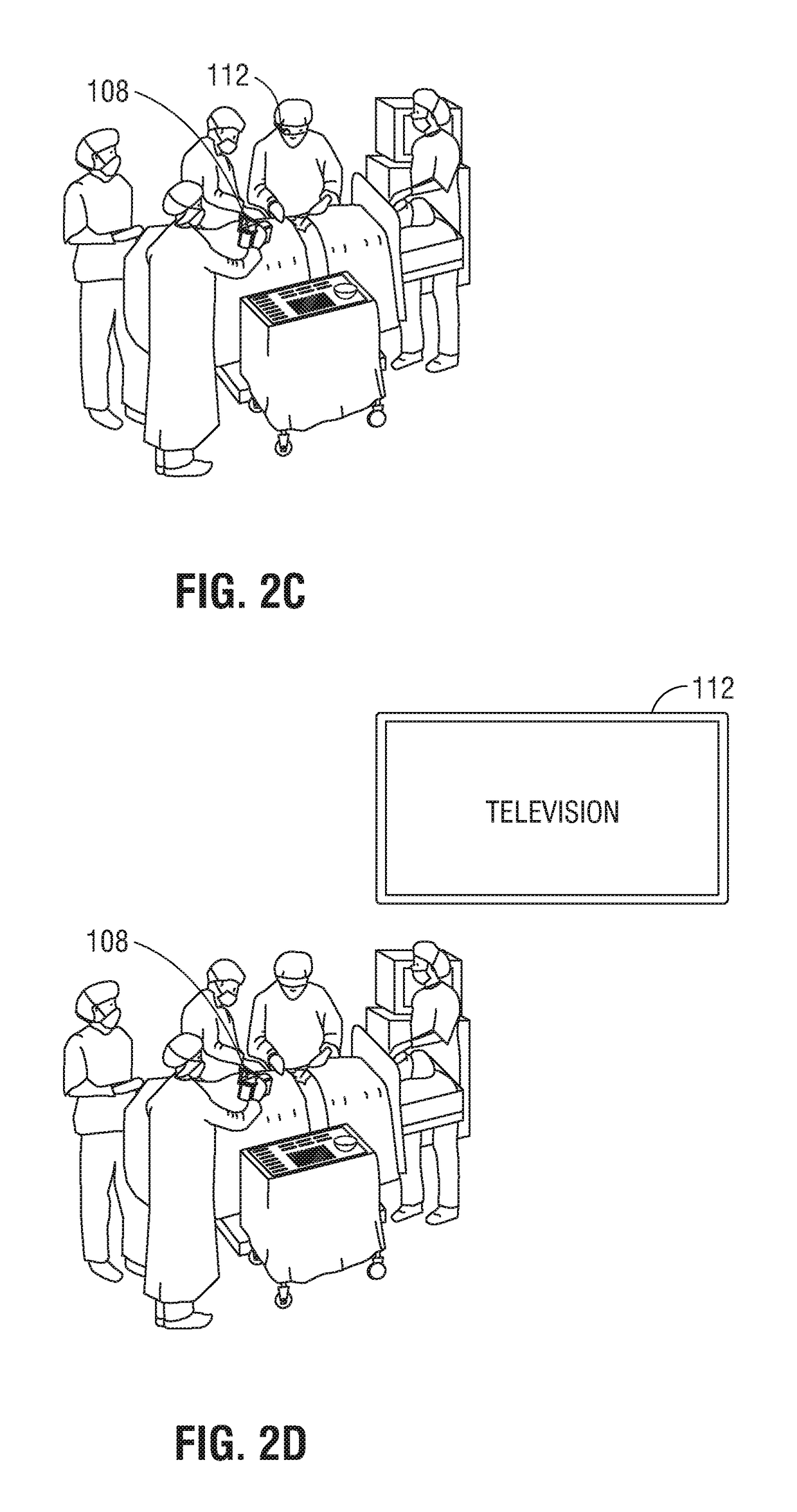
The present disclosure is directed to an augmented reality surgical system for viewing an augmented image of a region of interest during a surgical procedure. The system includes an image capture device that captures an image of the region of interest. A controller receives the image and applies at least one image processing filter to the image. The image processing filter includes a spatial decomposition filter that decomposes the image into spatial frequency bands. A temporal filter is applied to the spatial frequency bands to generate temporally filtered bands. An adder adds each band spatial frequency band to a corresponding temporally filtered band to generate augmented bands. A reconstruction filter generates an augmented image by collapsing the augmented bands. A display displays the augmented image to a user.
Owner:COVIDIEN LP
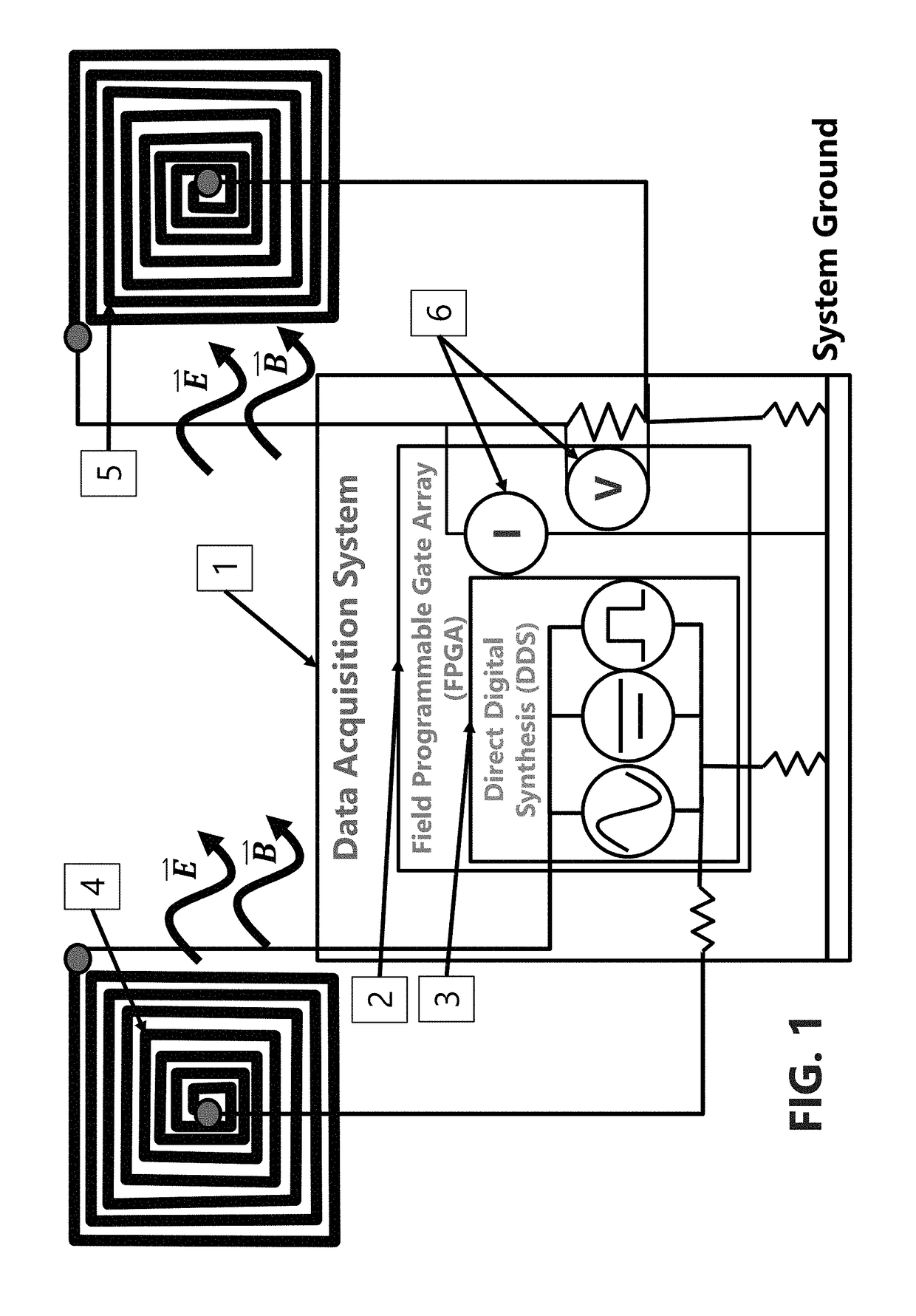
Electro-magneto volume tomography system and methodology for non-invasive volume tomography
InactiveUS20180325414A1Maximize surface areaMaximize number of turnReconstruction from projectionMaterial analysis by electric/magnetic meansCapacitanceImage resolution
A system and method capable of performing multiple types of non-invasive tomographic techniques. The system is capable, via electronic control, of detecting and imaging materials within a volume using electrical capacitance, displacement phase current, magnetic inductance, and magnetic pressure sensing. The system is also able to control the amplitude, phase, and frequency of individual electrode excitation to increase imaging resolution and phase detection. This allows many dimensions of non-invasive data to be captured without the need for multiple instruments or moving parts, at a high data capture rate.
Owner:TECH4IMAGING
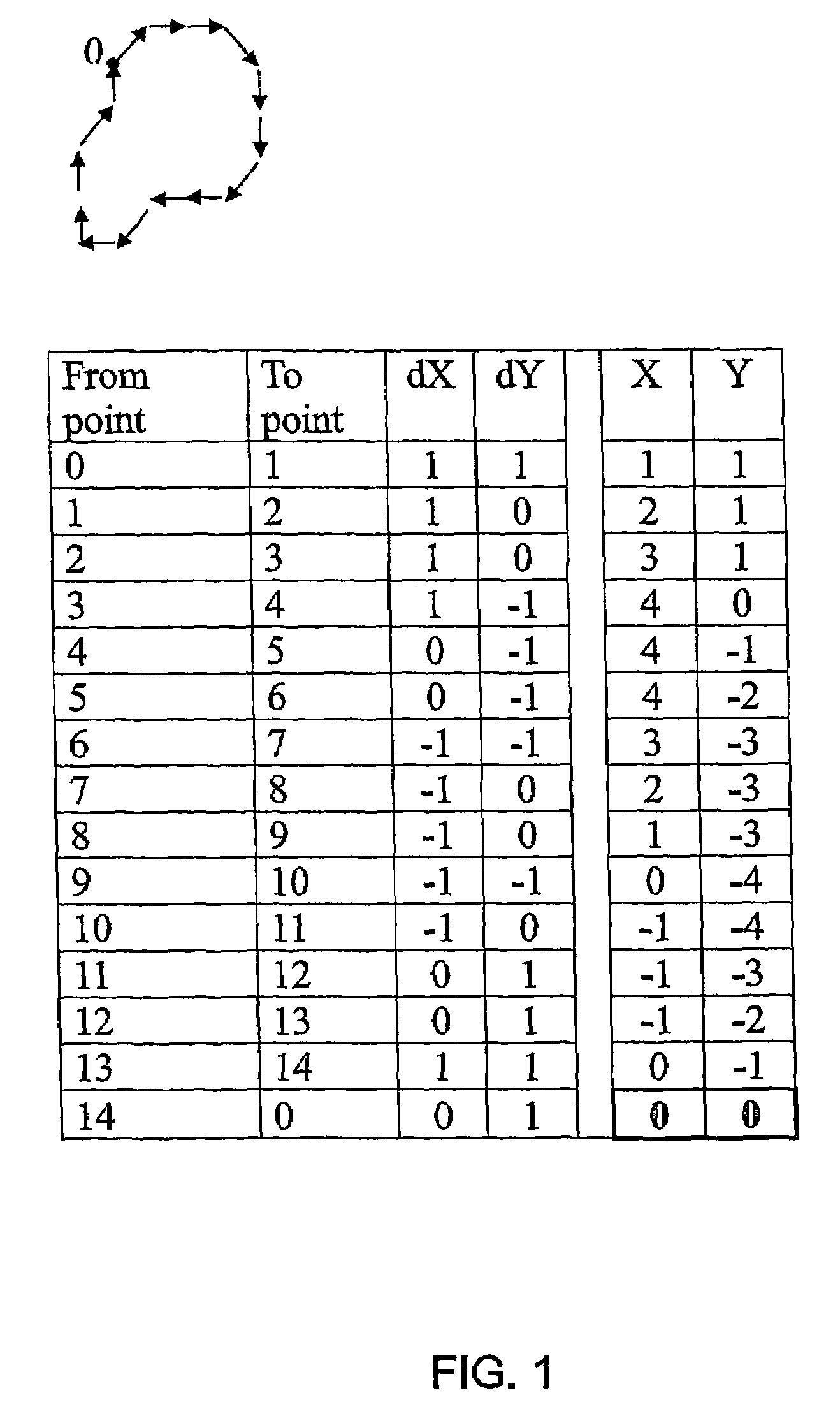
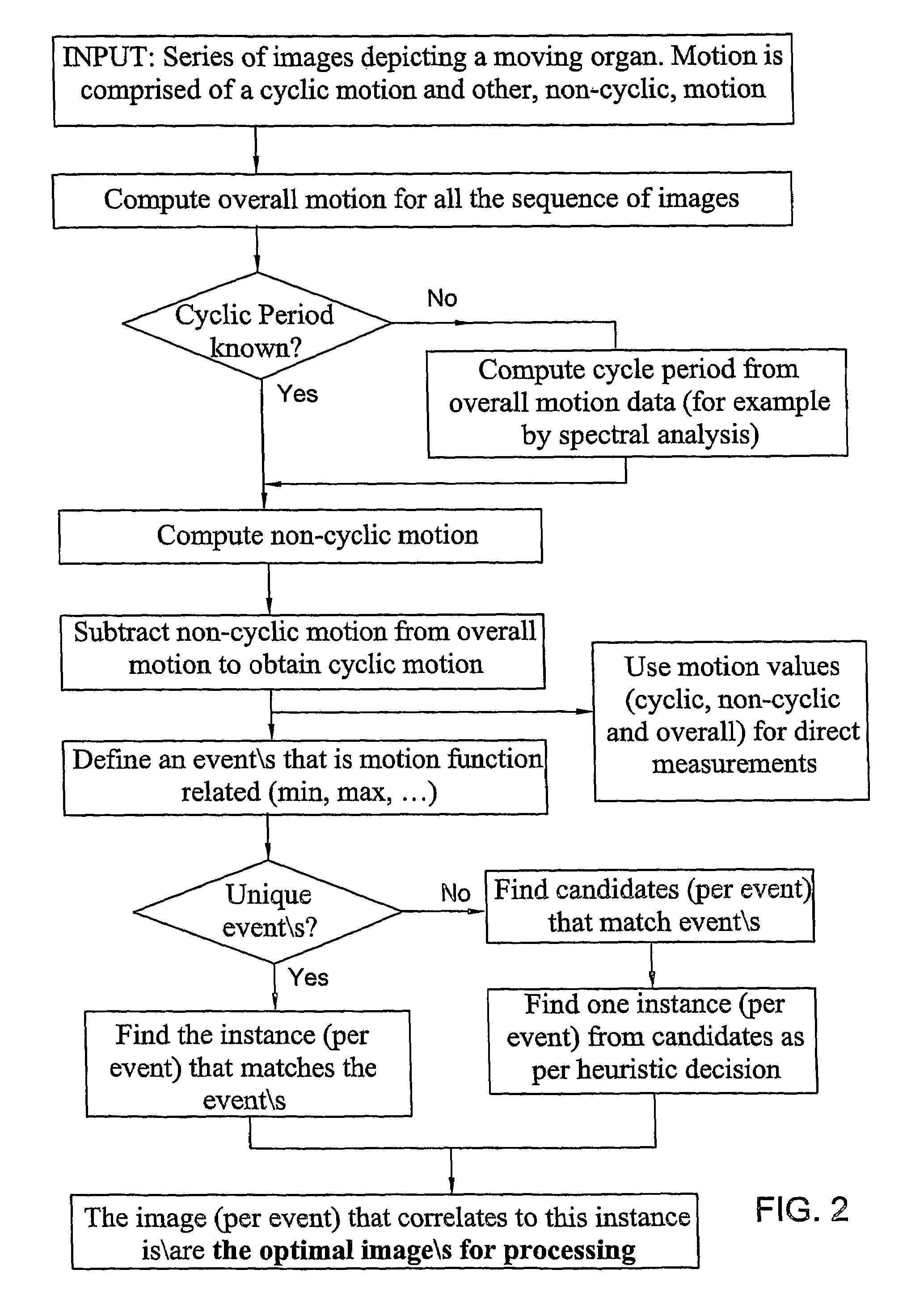
Method and system for identifying optimal image within a series of images that depict a moving organ
InactiveUS7587074B2Decrease and eliminate artifactReconstruction from projectionImage analysisComputer visionLow frequency
A method and system for quantifying a cyclic motion within a series of images depicting a moving object subject to composite motion containing a cyclic component and a non-cyclic component of lower frequency than the cyclic component. Composite motion is computed as well as the non-cyclic component as the integral of motion over a motion cycle. The non-cyclic component is subtracted from the composite motion so as to obtain the cyclic component
Owner:MEDTRONIC INC
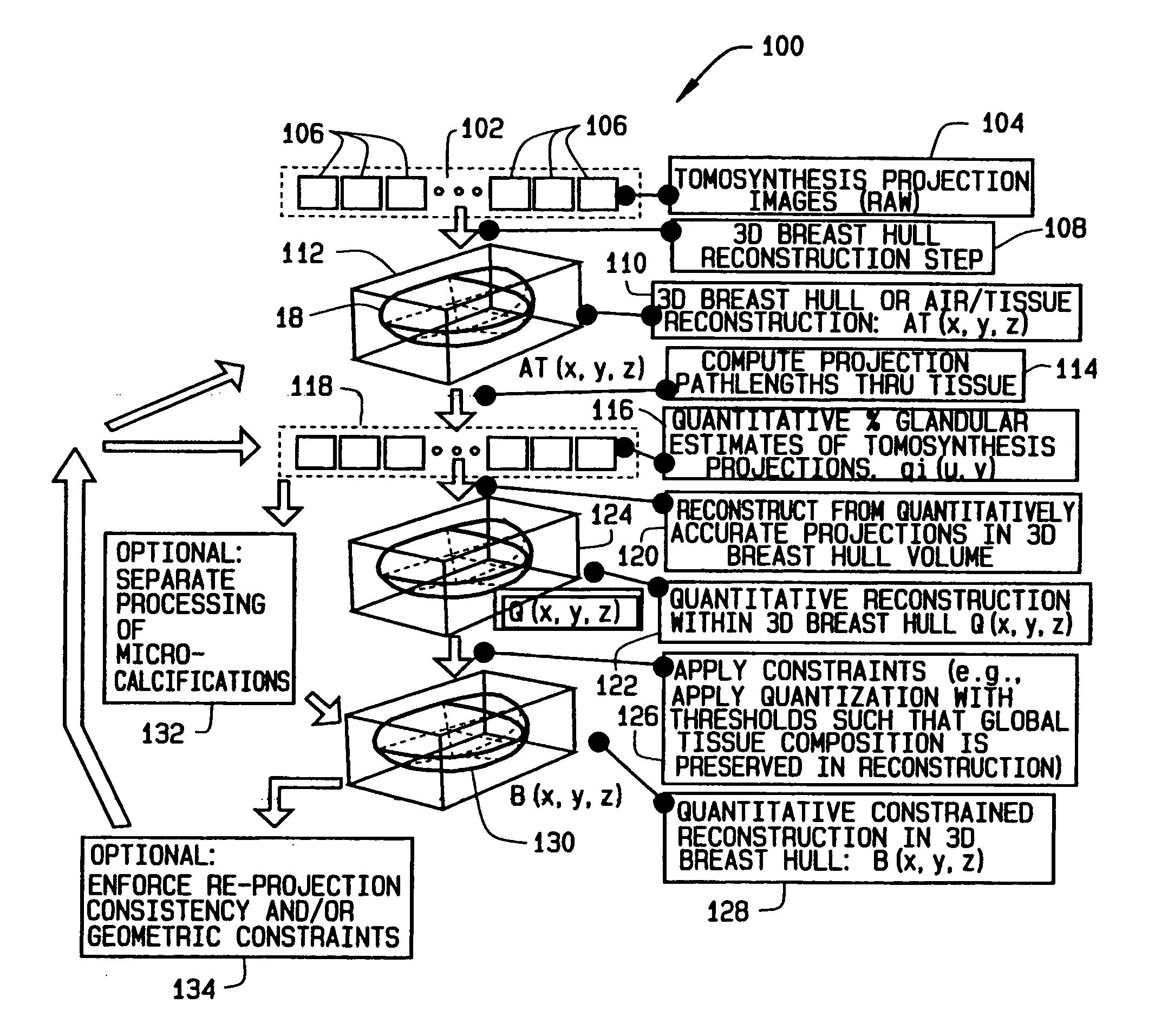
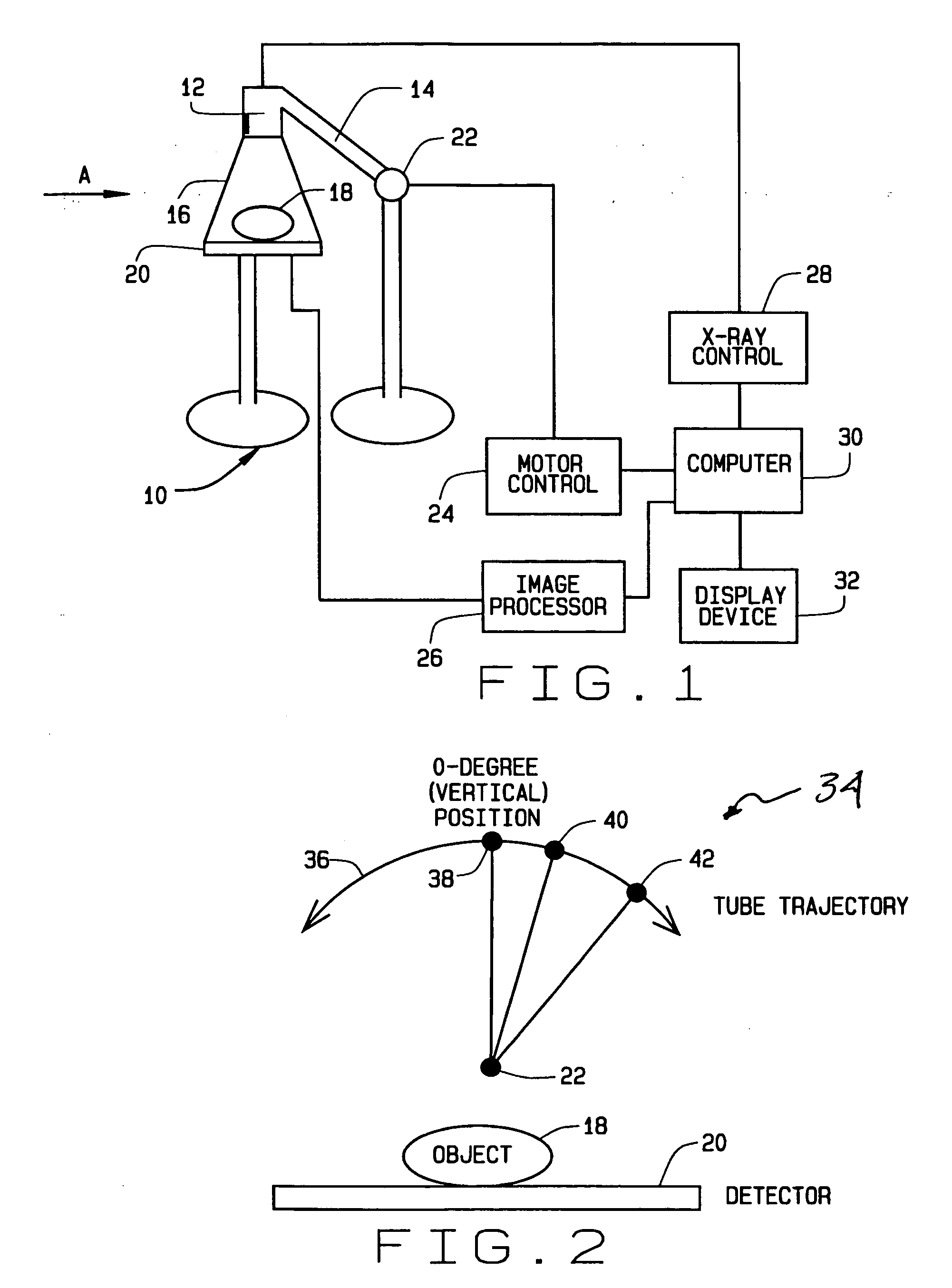
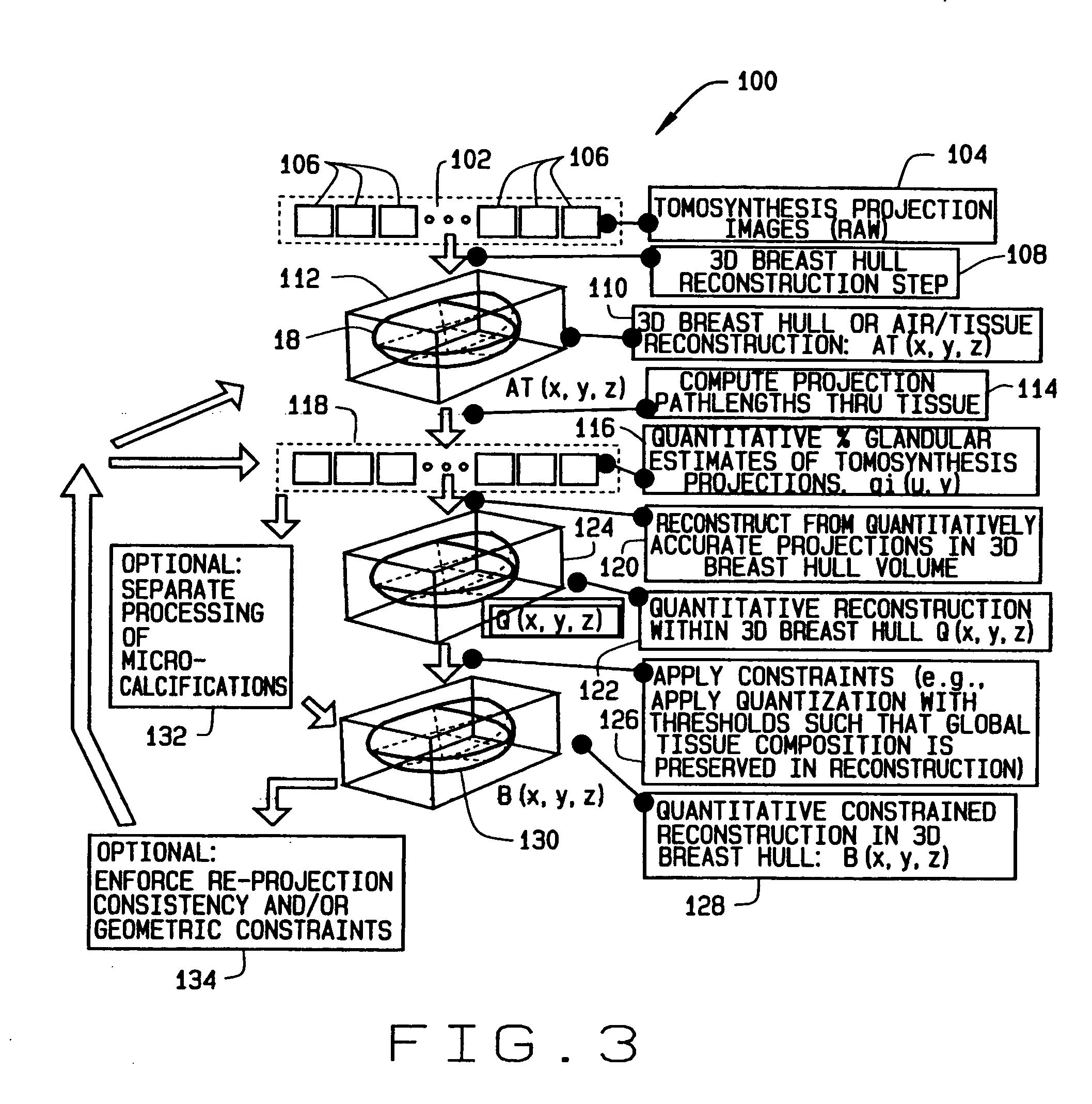
Methods and apparatus for reconstruction of volume data from projection data
ActiveUS20050135664A1Reconstruction from projectionCharacter and pattern recognitionTomosynthesisVoxel
Some configurations of method for reconstructing a volumetric image of an object include obtaining a tomosynthesis projection dataset of an object. The method also includes utilizing the tomosynthesis projection dataset and additional information about the object to minimize a selected energy function or functions to satisfy a selected set of constraints. Alternatively, constraints are applied to a reconstructed volumetric image in order to obtain an updated volumetric image. A 3D volume representative of the imaged object is thereby obtained in which each voxel is reconstructed and a correspondence indicated to a single one of the component material classes.
Owner:GE MEDICAL SYST GLOBAL TECH CO LLC
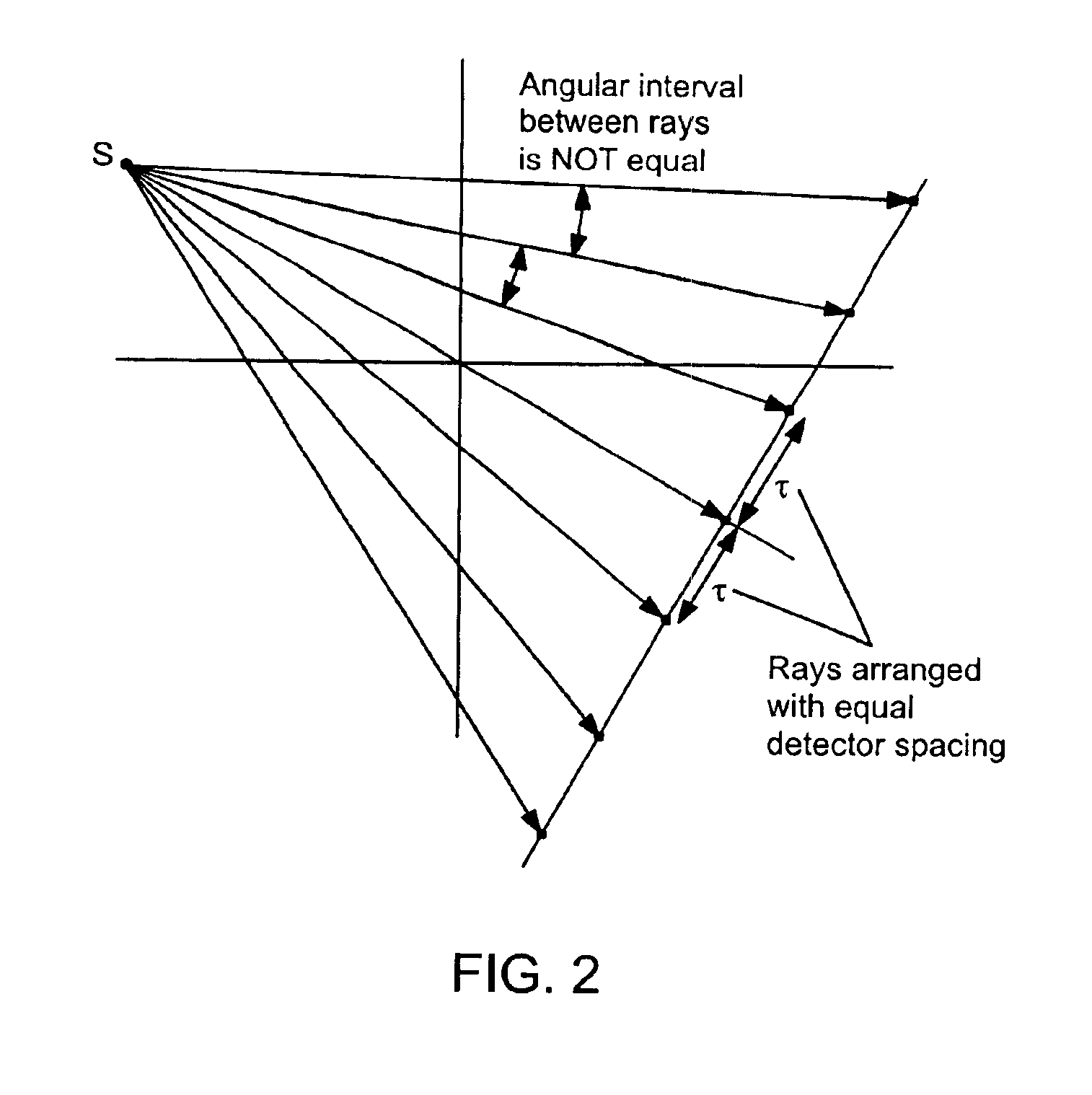
Apparatus and method for reconstruction of volumetric images in a divergent scanning computed tomography system
ActiveUS7106825B2Reconstruction from projectionMaterial analysis using wave/particle radiationDetector arrayComputing tomography
An apparatus and method for reconstructing image data for a region are described. A radiation source and multiple one-dimensional linear or two-dimensional planar area detector arrays located on opposed sides of a region angled generally along a circle centered at the radiation source are used to generate scan data for the region from a plurality of diverging radiation beams, i.e., a fan beam or cone beam. Individual pixels on the discreet detector arrays from the scan data for the region are reprojected onto a new single virtual detector array along a continuous equiangular arc or cylinder or equilinear line or plane prior to filtering and backprojecting to reconstruct the image data.
Owner:MEDTRONIC NAVIGATION
Tomography-Based and MRI-Based Imaging Systems
InactiveUS20110142316A1Comparable image qualityImproved temporalReconstruction from projectionCharacter and pattern recognitionTomosynthesisElastography
Tomography limitations in vivo due to incomplete, inconsistent and intricate measurements require solution of inverse problems. The new strategies disclosed in this application are capable of providing faster data acquisition, higher image quality, lower radiation dose, greater flexibility, and lower system cost. Such benefits can be used to advance research in cardiovascular diseases, regenerative medicine, inflammation, and nanotechnology. The present invention relates to the field of medical imaging. More particularly, embodiments of the invention relate to methods, systems, and devices for imaging, including tomography-based and MRI-based applications. For example, included in embodiments of the invention are compressive sampling based tomosynthesis methods, which have great potential to reduce the overall x-ray radiation dose for a patient. To name a few, compressive sensing based carbon nano-tube based interior tomosynthesis systems, tomography-based dynamic cardiac elastography systems, cardiac elastodynamic biomarkers from interior MR imaging, exact and stable interior ROI reconstructions for radial MRI, and interior reconstruction based ultrafast tomography systems are provided.
Owner:WANG GE +5
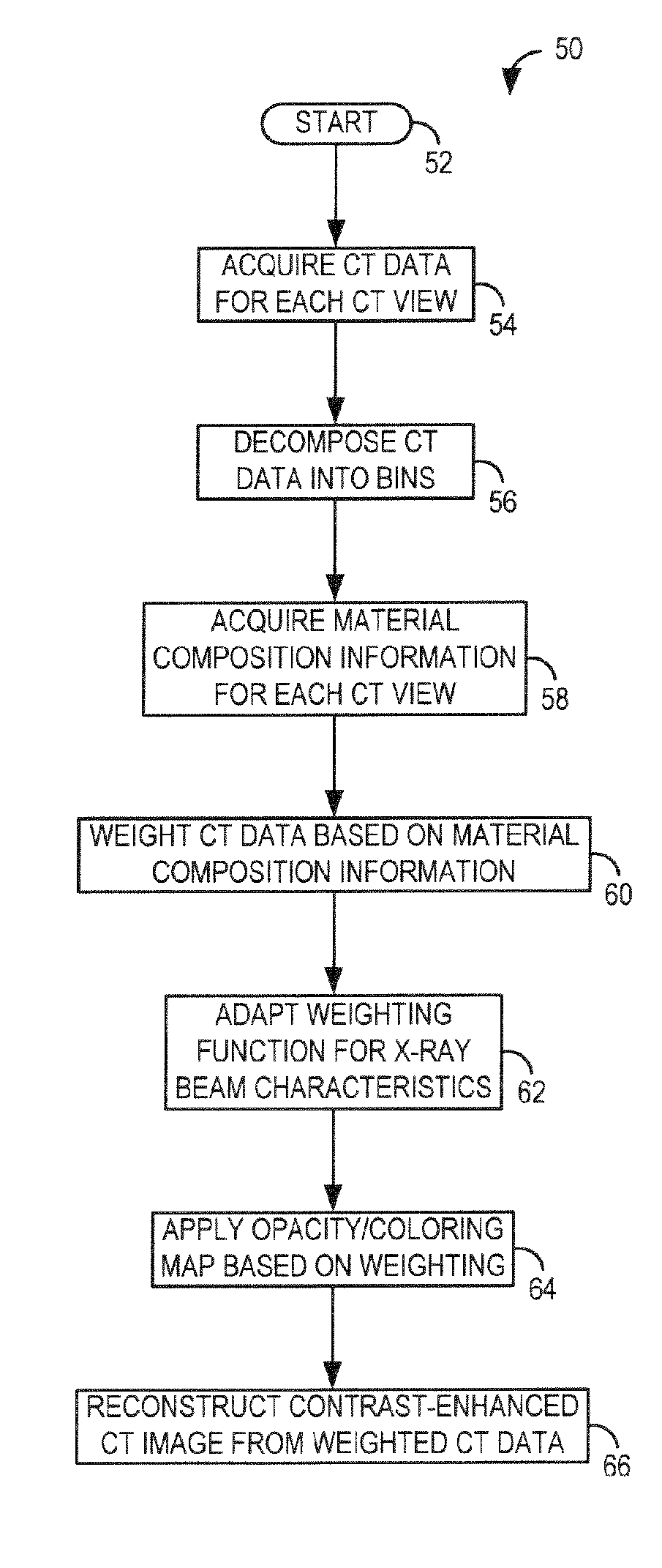
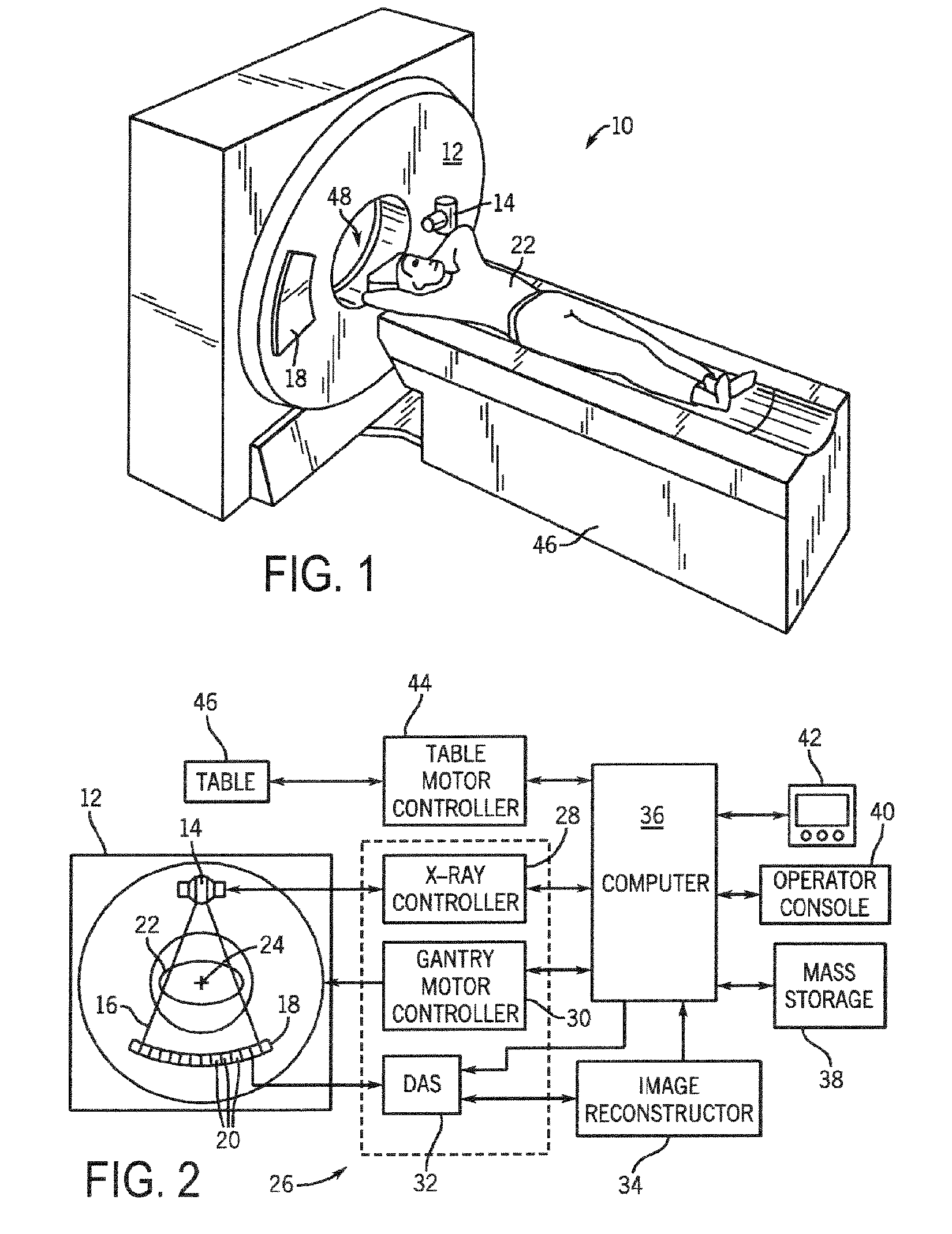
System and method for acquisition and reconstruction of contrast-enhanced, artifact-reduced CT images
ActiveUS20060109949A1Reconstruction from projectionMaterial analysis using wave/particle radiationView basedPhoton
A system and method are disclosed for reconstructing contrast-enhanced CT images that are substantially free of beam-hardening artifacts. An imaging system includes a radiation source configured to project radiation toward an object to be scanned and an energy discriminating detector assembly having a plurality of detector elements and configured to detect radiation emitted by the radiation source and attenuated by the object to be scanned. The imaging system also includes computer programmed to count a number of photons detected by each detector element and associate an energy value to each counted photon and determine a material composition of a CT view from the number of photons counted and the energy value associated with each counted photon. The computer is also programmed to apply a weighting to the CT view based on the material composition of the CT view and reconstruct an image with differential weighting based on the weighting of the CT view.
Owner:GENERAL ELECTRIC CO
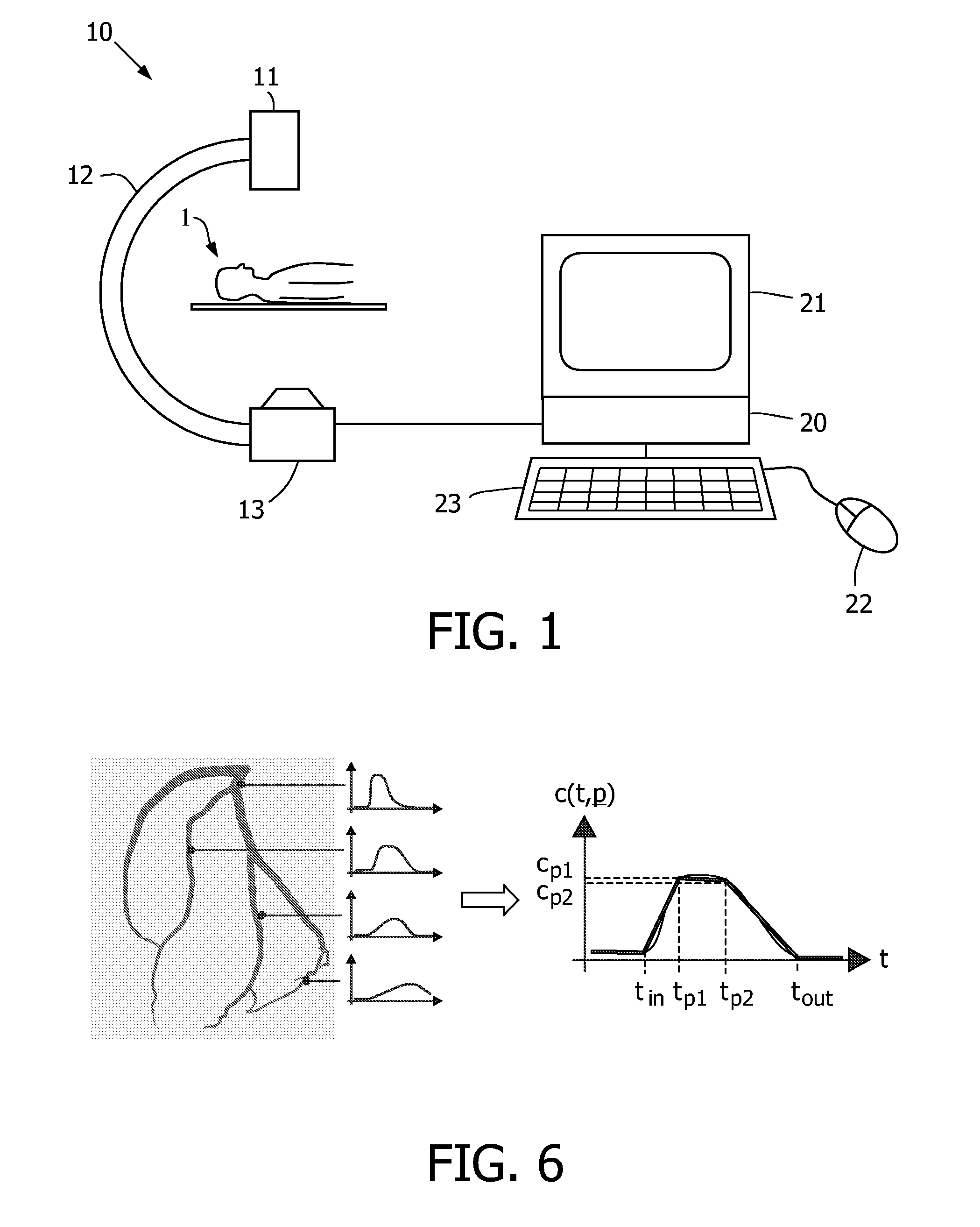
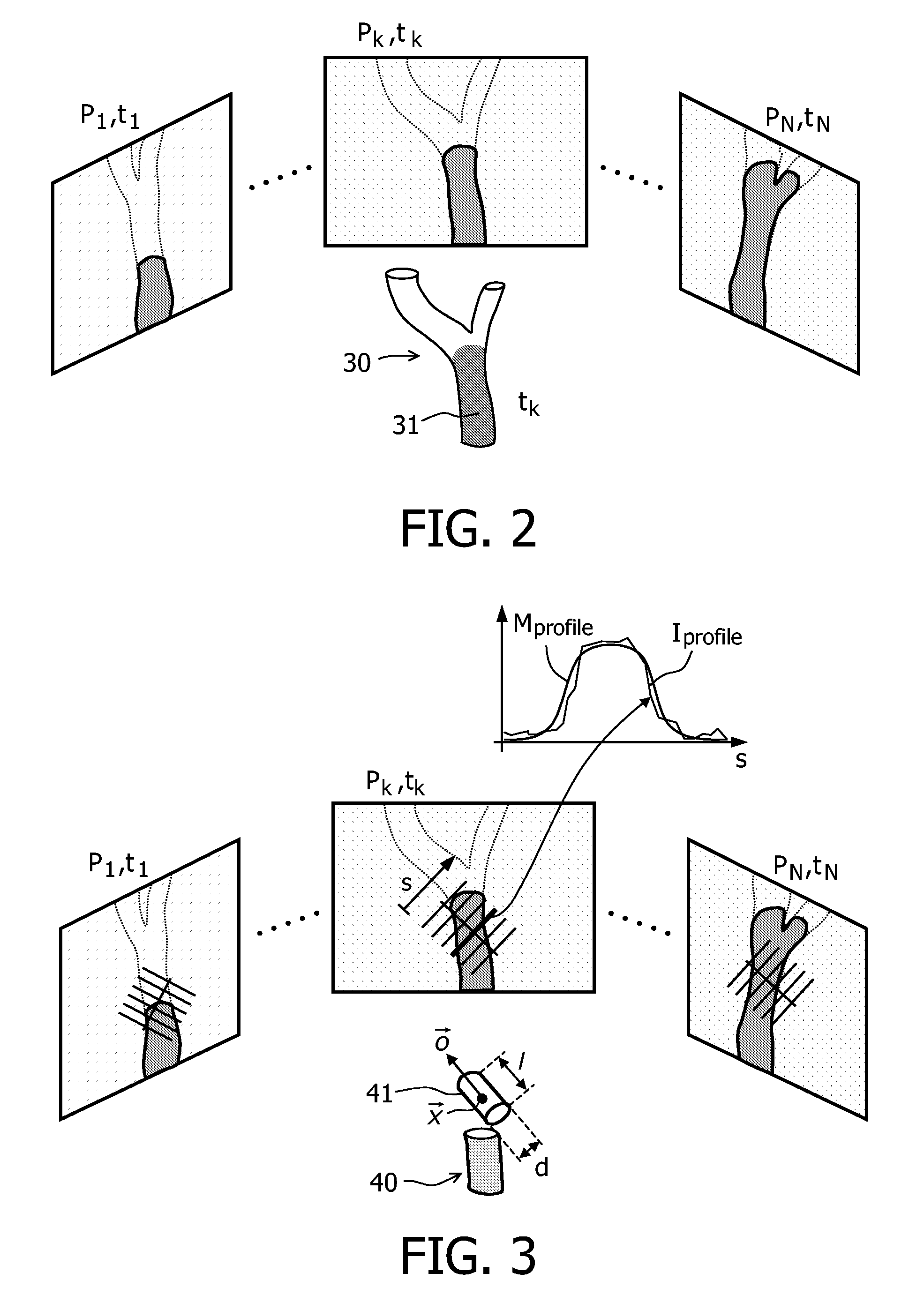
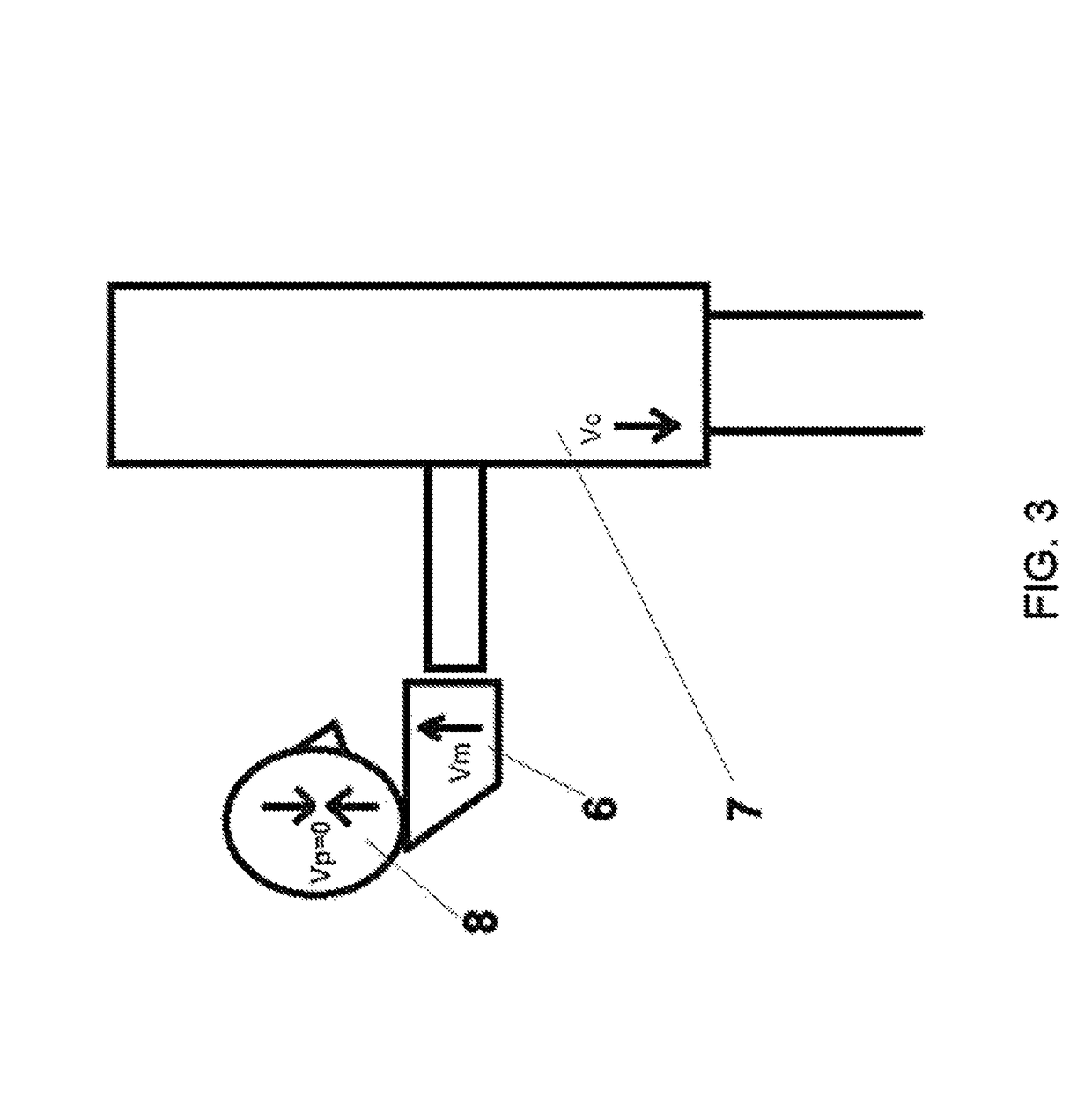
System for the determination of vessel geometry and flow characteristics
ActiveUS7738626B2Improve accuracyRelieve pressureImage enhancementReconstruction from projectionMarine engineeringX-ray
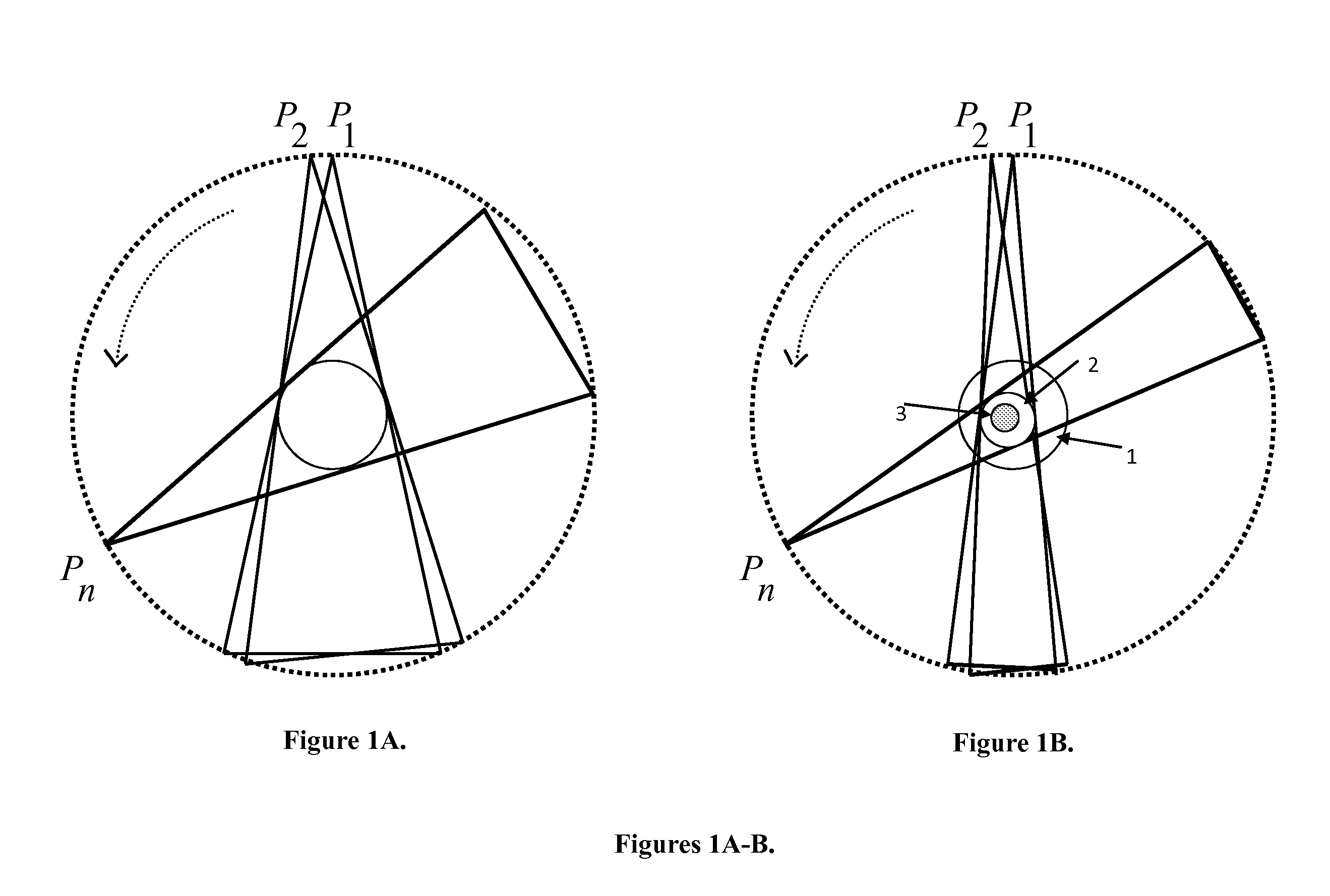
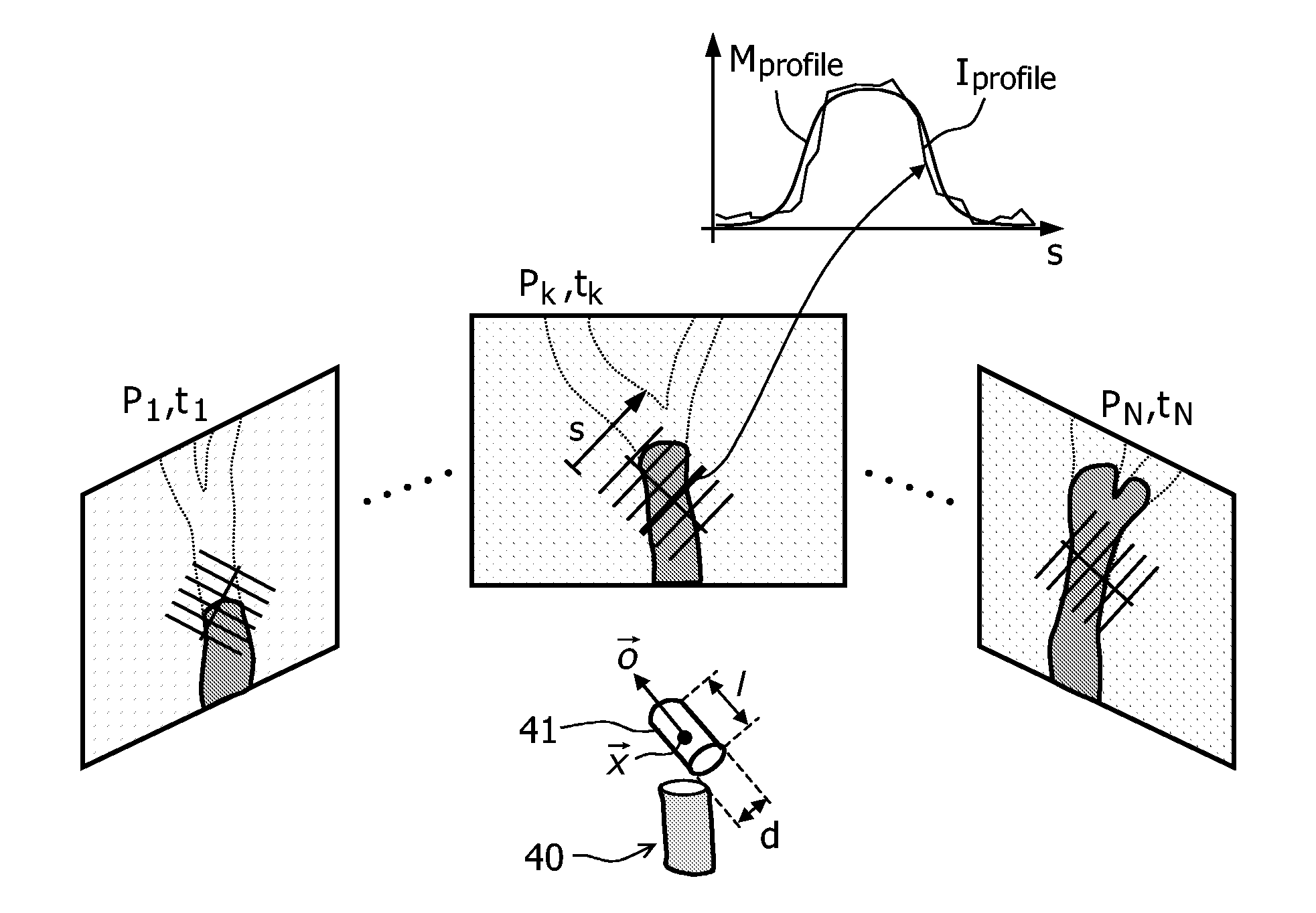
The invention relates to a method and a system for the simultaneous reconstruction of the three-dimensional vessel geometry and the flow characteristics in a vessel system. According to one realization of the method, vessel segments (41) of a parametric models are fitted to differently oriented X-ray projections (P1, Pk, PN) of the vessel system that are generated during the passage of a bolus of contrast agent, wherein the fitting takes the imaged contrast agent dynamics and physiological a priori knowledge into account. In an alternative embodiment, the vessel geometry is reconstructed progressively along each vessel, wherein a new segment of a vessel is added based on the continuity of the vessel direction, vessel radius and reconstructed contrast agent dynamics.
Owner:KONINKLIJKE PHILIPS ELECTRONICS NV
System and method for three-dimensional image rendering and analysis
InactiveUS20080205717A1Reduce decreaseReduce contributionImage enhancementReconstruction from projectionImaging analysis3d image
The present invention relates to methods and systems for conducting three-dimensional image analysis and diagnosis and possible treatment relating thereto. The invention includes methods of handling signals containing information (data) relating to three-dimensional representation of objects scanned by a scanning medium. The invention also includes methods of making and analyzing volumetric measurements and changes in volumetric measurements which can be used for the purpose of diagnosis and treatment.
Owner:CORNELL RES FOUNDATION INC
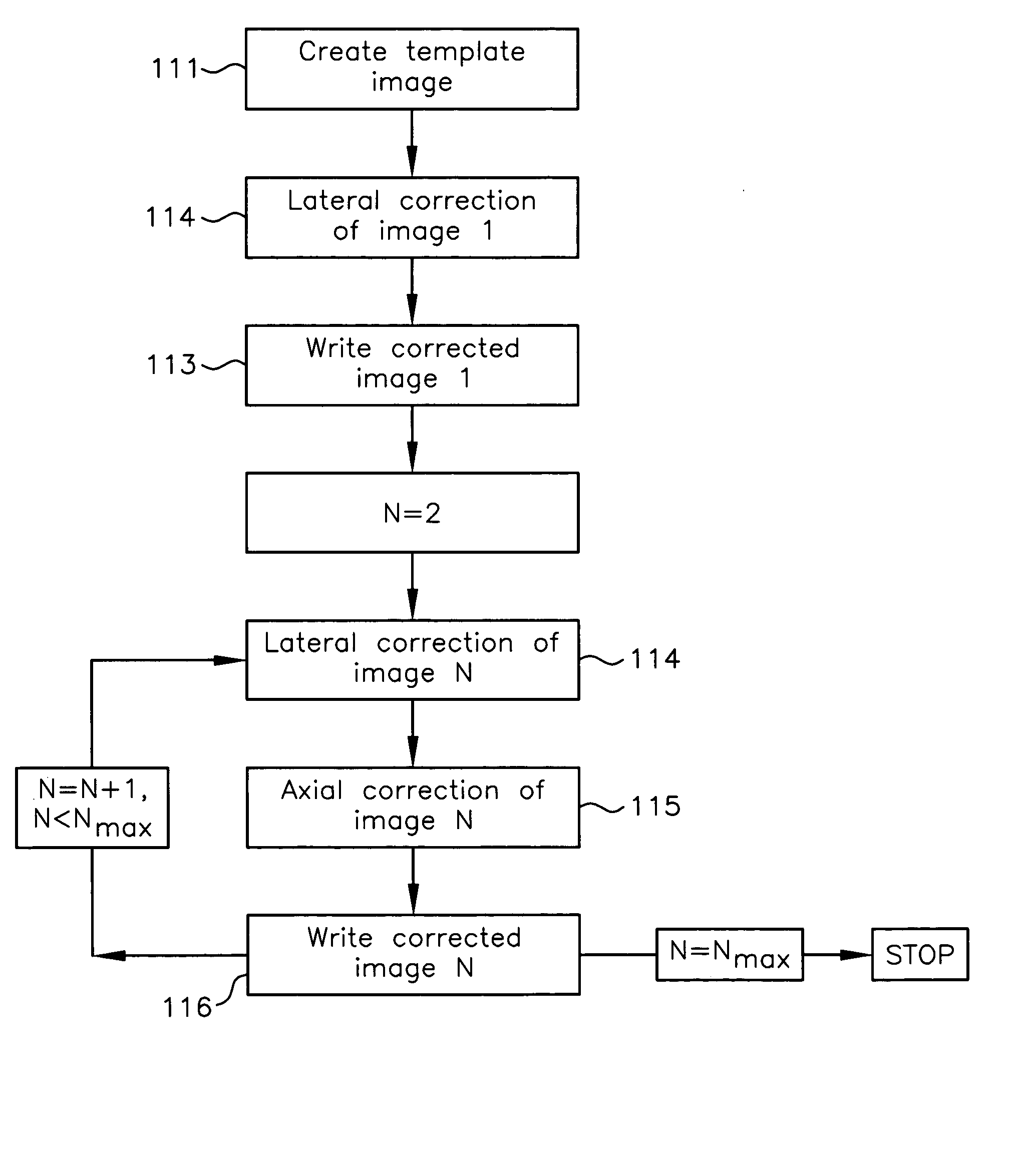
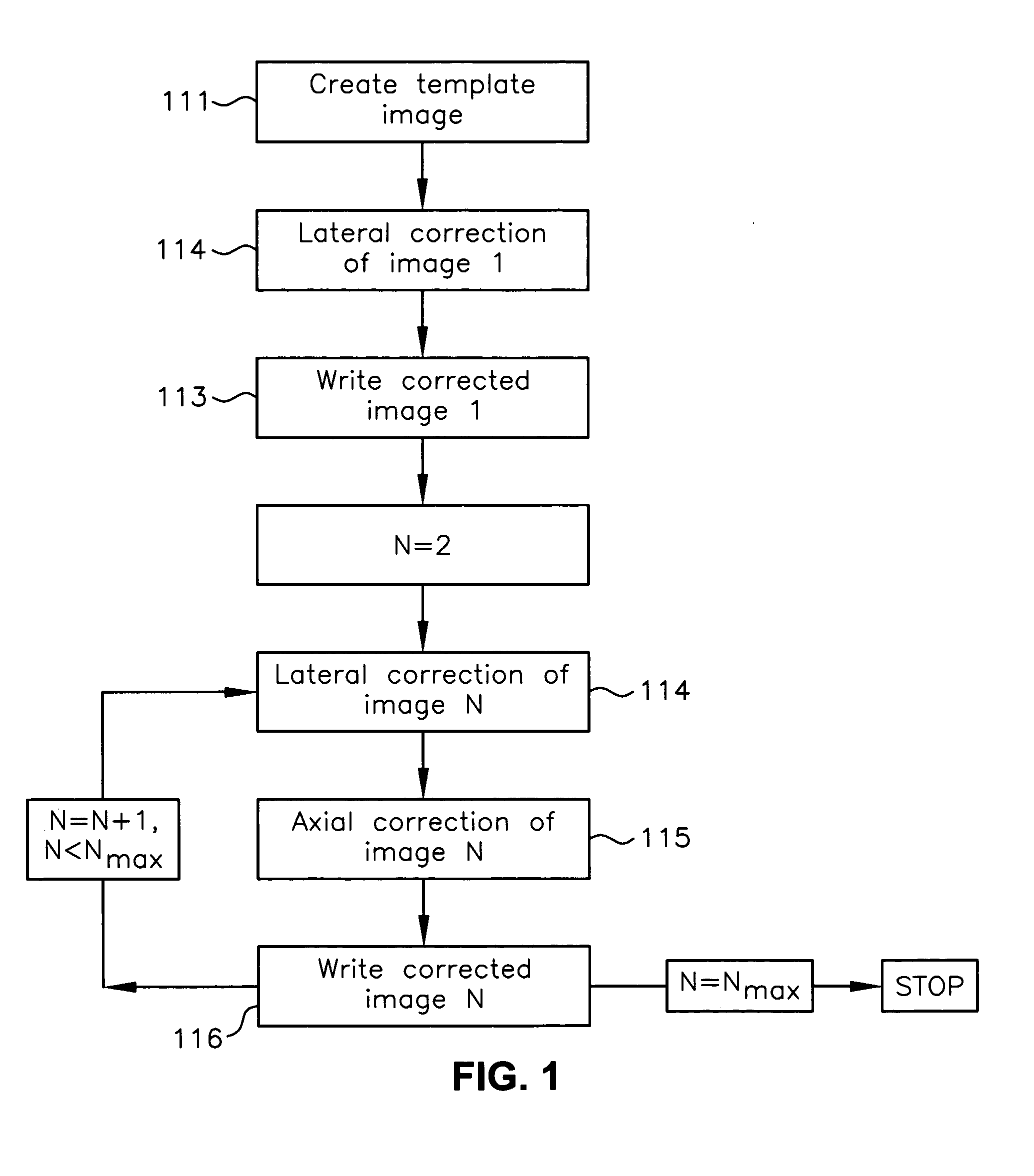
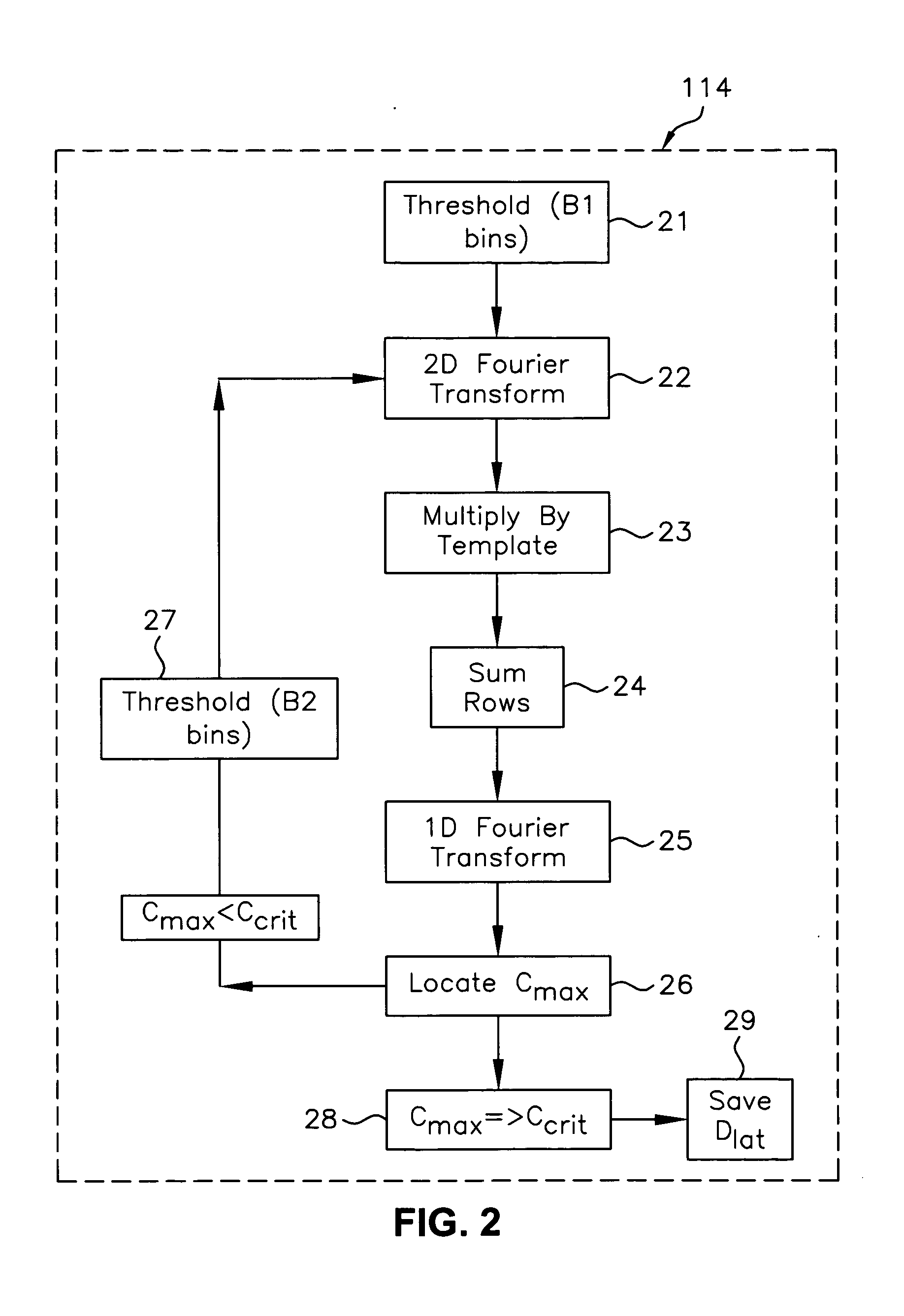
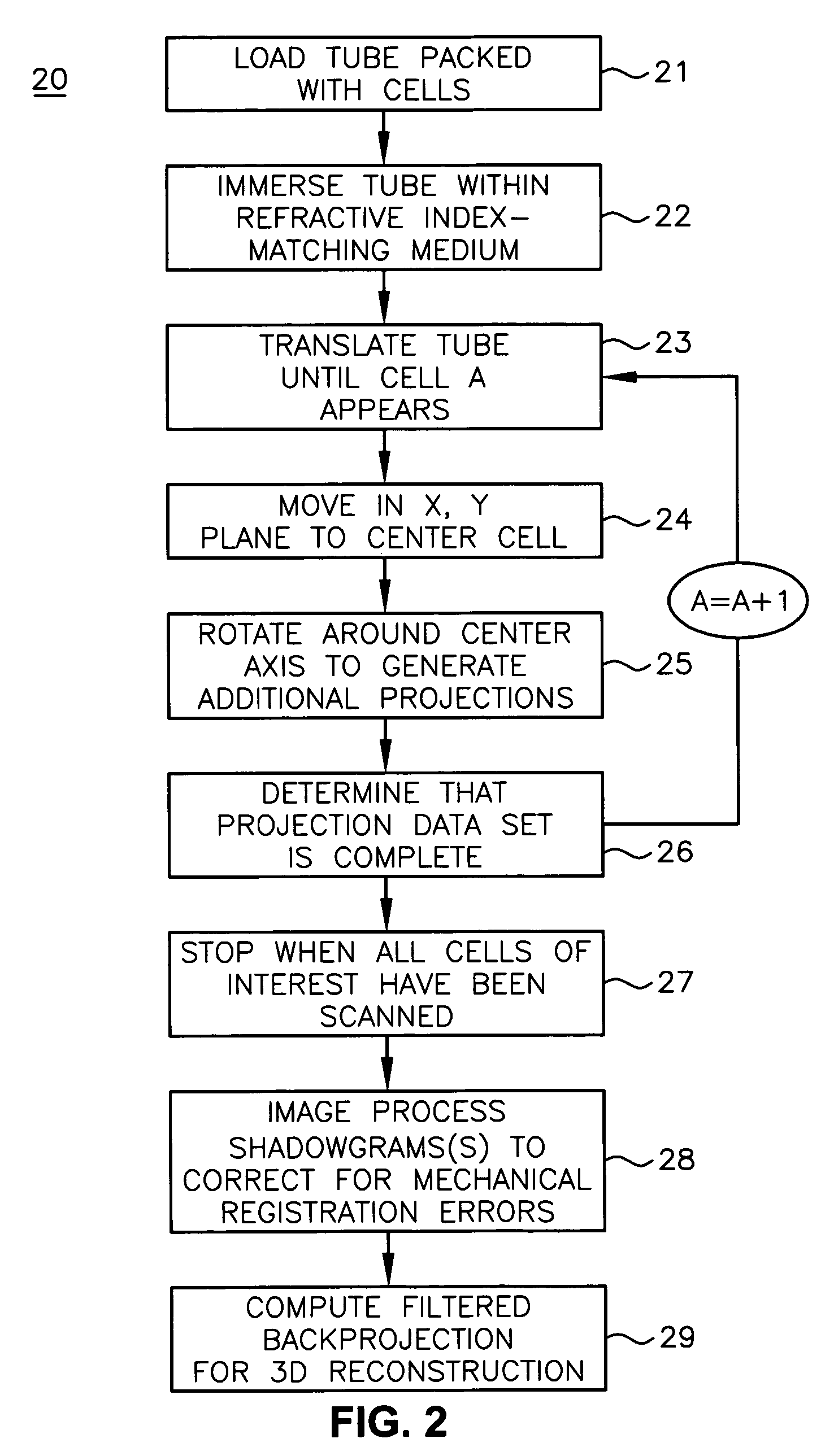
Method for correction of relative object-detector motion between successive views
Registration correction for optical tomographic imaging in three dimensions. An object of interest is illuminated to produce an image. A lateral offset correction value is determined for the image. An axial offset correction value is determined for the image. The lateral offset correction value and the axial offset correction value are applied to the image to produce a corrected file image.
Owner:VISIONGATE
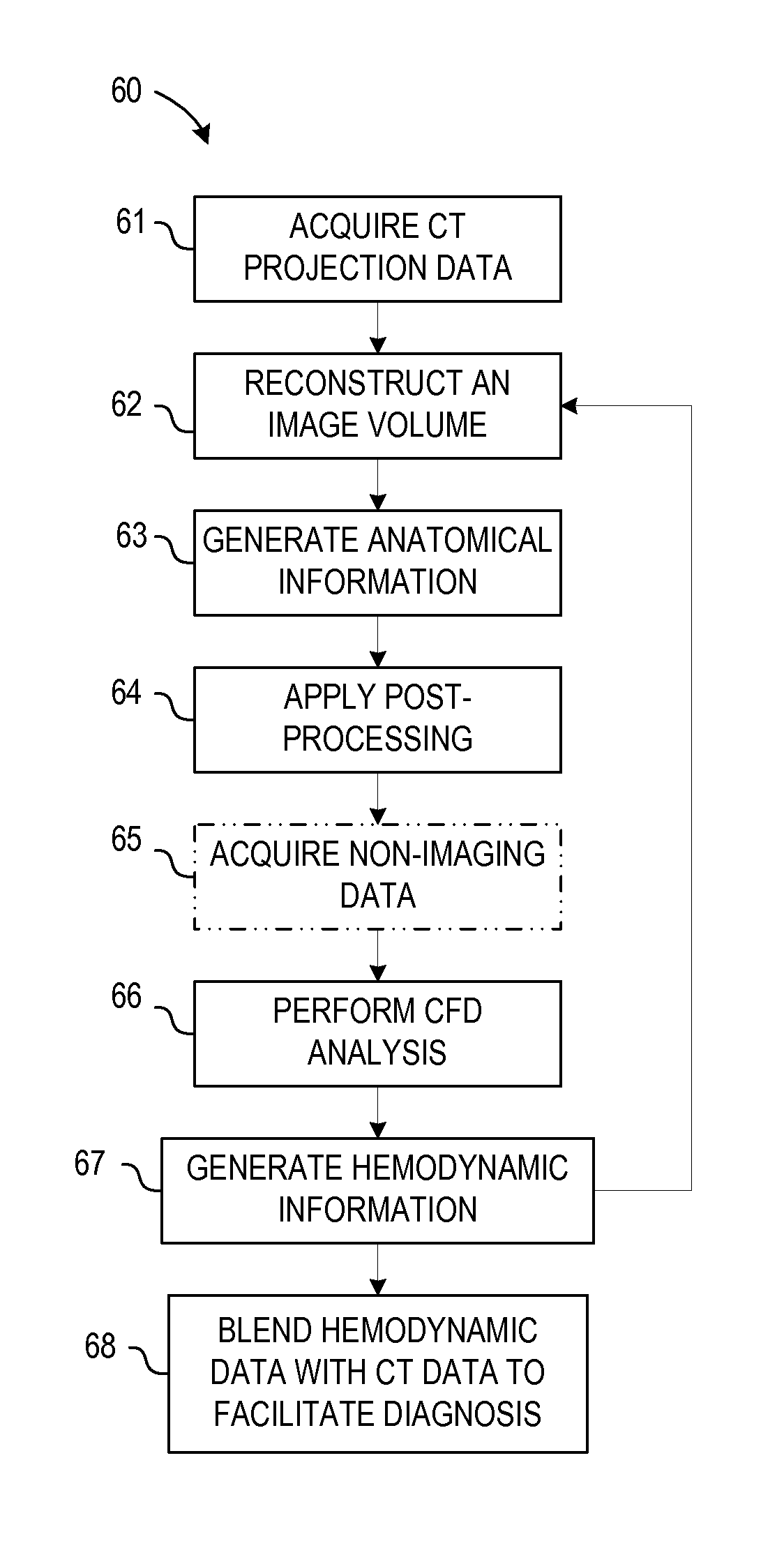
System and method for estimating vascular flow using ct imaging
A system and method for estimating vascular flow using CT imaging include a computer readable storage medium having stored thereon a computer program comprising instructions, which, when executed by a computer, cause the computer to acquire a first set of data comprising anatomical information of an imaging subject, the anatomical information comprises information of at least one vessel. The instructions further cause the computer to process the anatomical information to generate an image volume comprising the at least one vessel, generate hemodynamic information based on the image volume, and acquire a second set of data of the imaging subject. The computer is also caused to generate an image comprising the hemodynamic information in combination with a visualization based on the second set of data.
Owner:GENERAL ELECTRIC CO
System, method and computer-accessible medium for providing a panoramic cone beam computed tomography (CBCT)
InactiveUS20150213633A1Image enhancementReconstruction from projectionProjection imageCone beam computed tomography
Exemplary devices, procedures and computer-readable mediums for providing a projection image associated with at least one target. The projection image can be formed from a plurality of locations of a source arrangement. At each source location, a plurality of panoramic projection images associated with a target can be acquired. At least two of the panoramic projection images can be obtained at view angles which are different from one another. These panoramic projection images can be stitched together or otherwise combined. A resulting image can then be generated using a computed tomography procedure based on the stitched or combined projection images that are generated at the plurality of location.
Owner:THE TRUSTEES OF COLUMBIA UNIV IN THE CITY OF NEW YORK
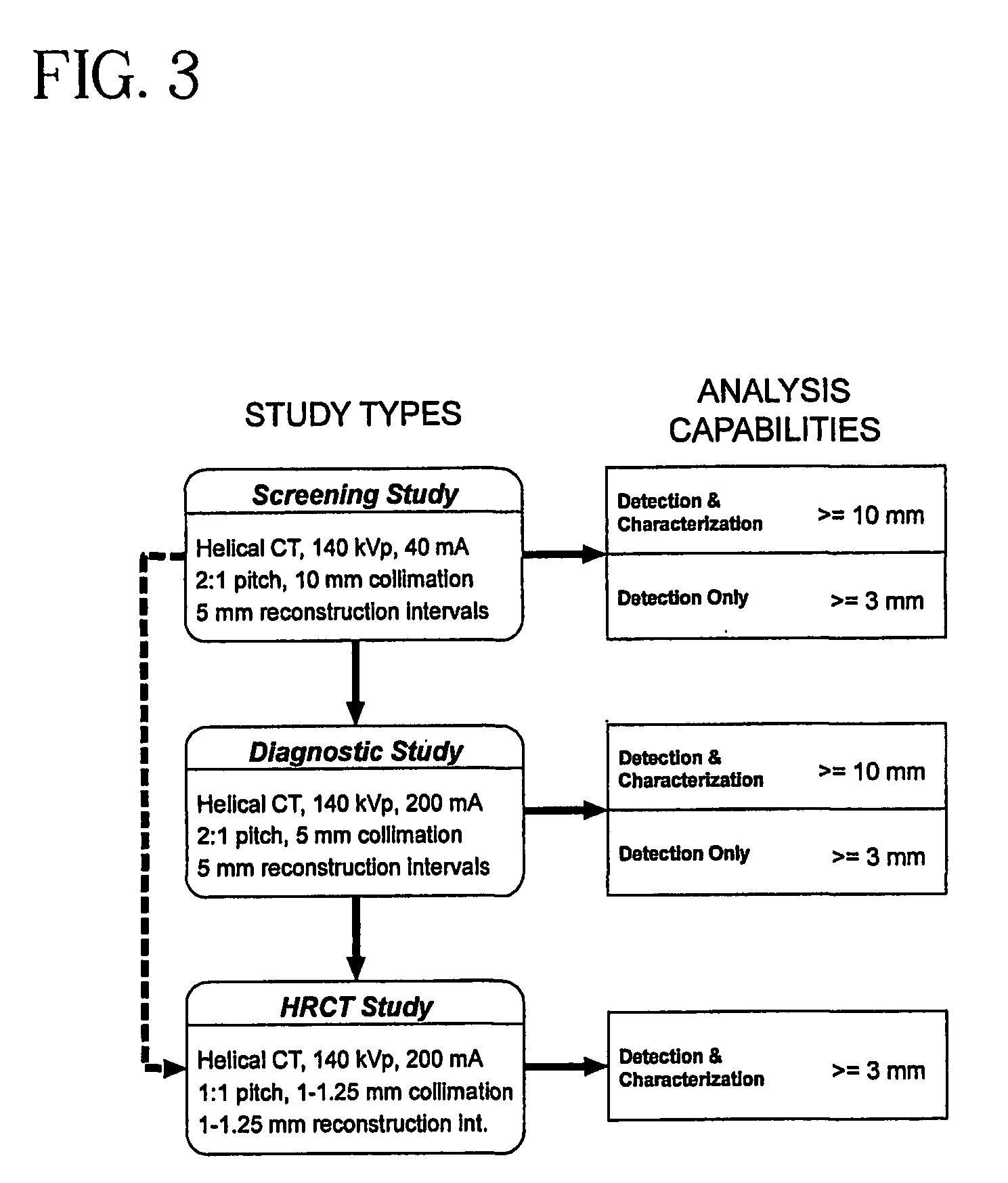
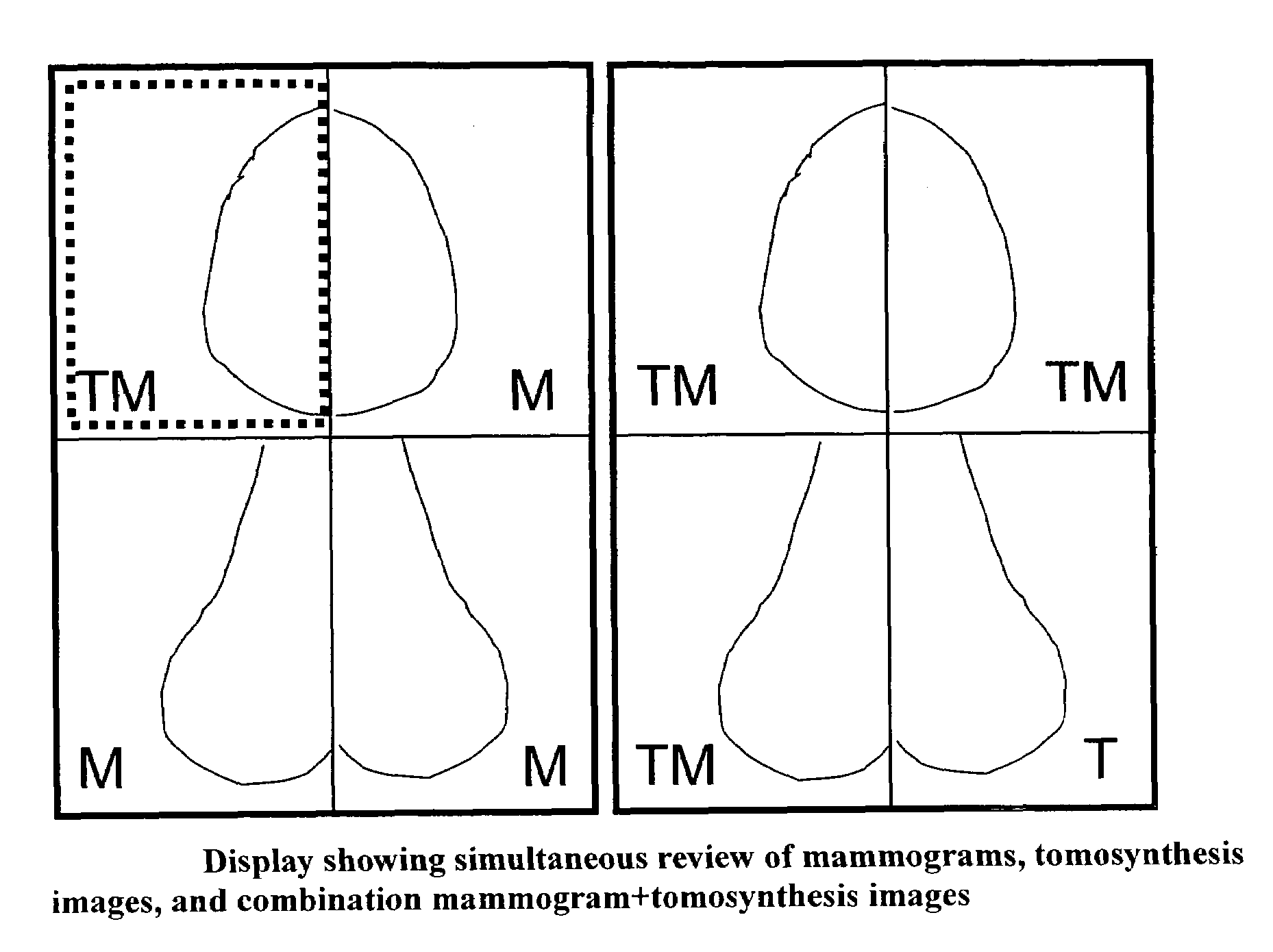
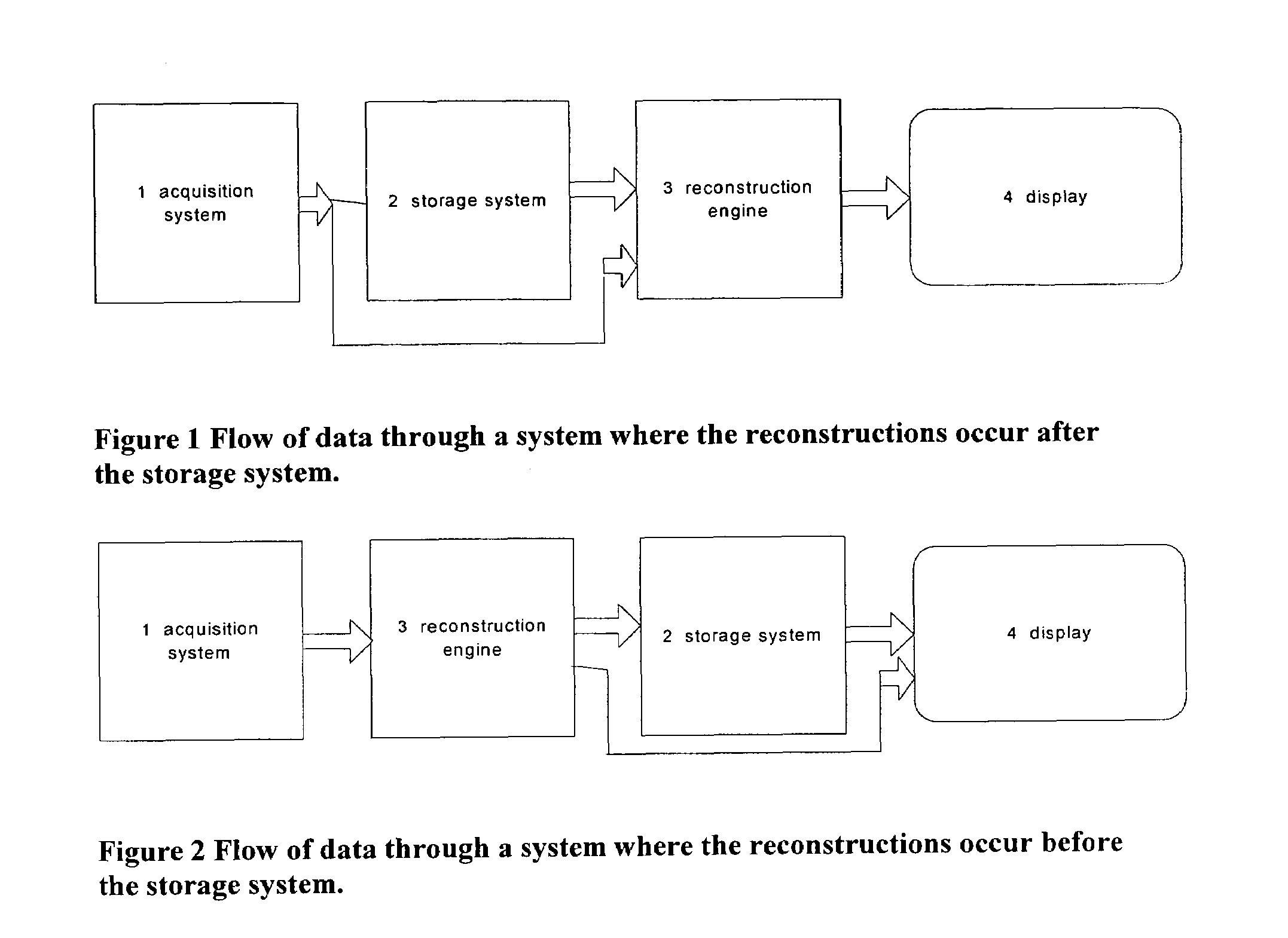
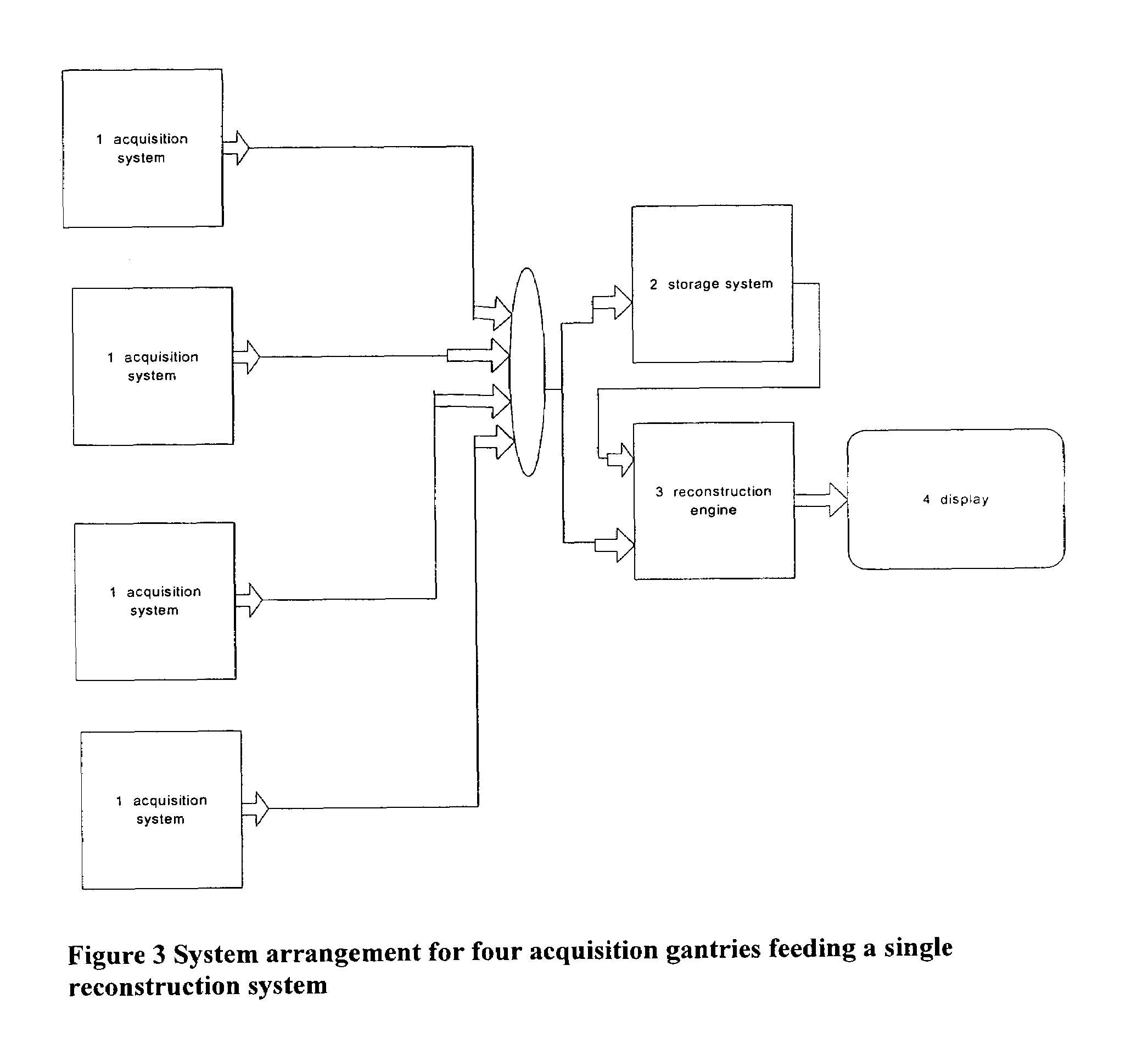
Image Handling and display in X-ray mammography and tomosynthesis
InactiveUS20080019581A1Easy to identifyImprove assessmentImage enhancementReconstruction from projectionTomosynthesisProjection image
A method and system for acquiring, processing, storing, and displaying x-ray mammograms Mp tomosynthesis images Tr representative of breast slices, and x-ray tomosynthesis projection images Tp taken at different angles to a breast, where the Tr images are reconstructed from Tp images
Owner:HOLOGIC INC
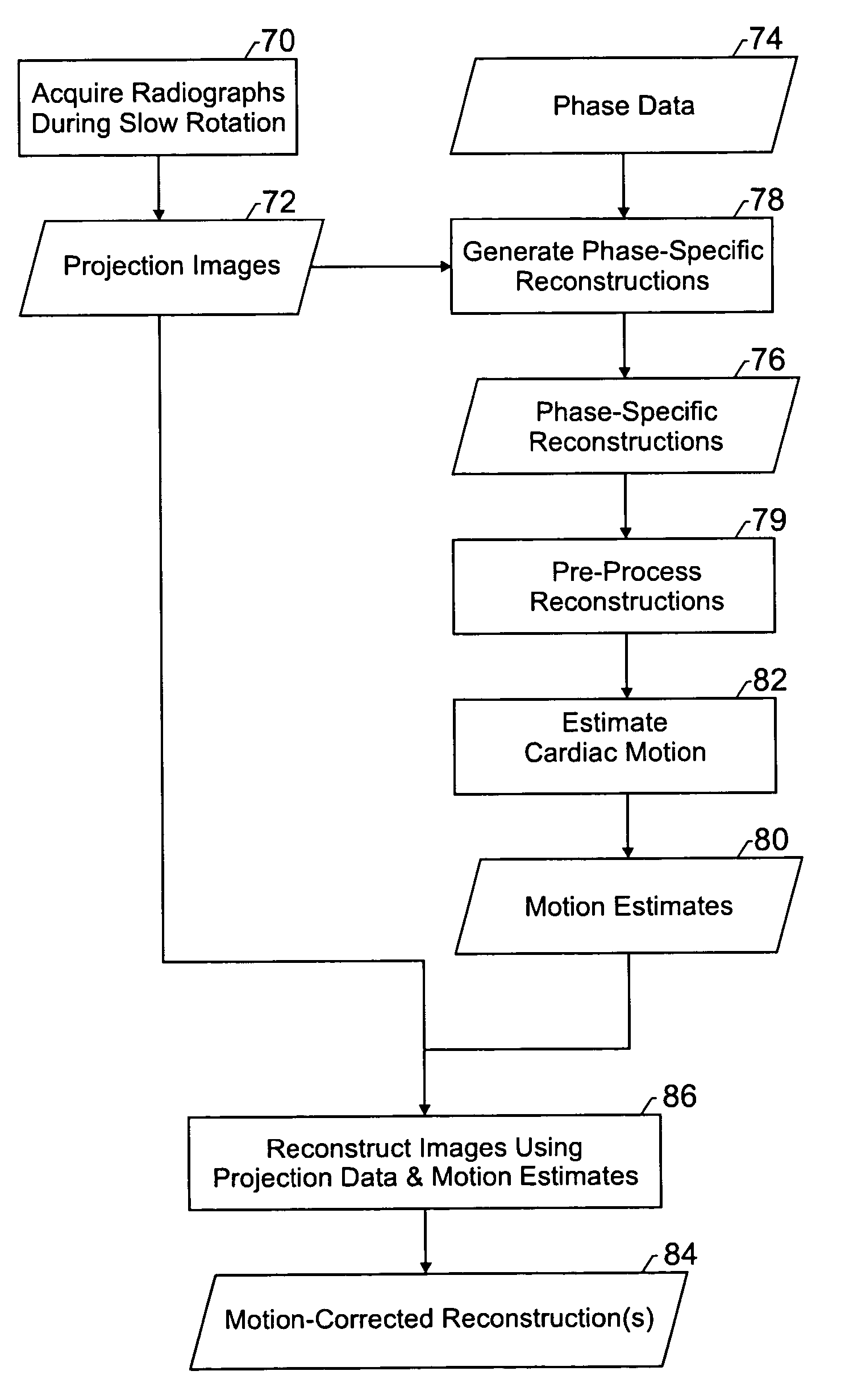
Method and apparatus for correcting motion in image reconstruction
A plurality of projection images are acquired over an angular range during the slow rotation of a C-arm gantry having a source and detector. Phase-specific reconstructions are generated from the plurality of projections, wherein each phase-specific reconstruction is generated generally from projections acquired at or near the respective phase. In one embodiment, a plurality of motion estimates are generated based upon the phase-specific reconstructions. One or more motion-corrected reconstructions may be generated using the respective motion estimates and projections. The motion-corrected reconstructions may be associated to form motion-corrected volume renderings.
Owner:GENERAL ELECTRIC CO
Computed tomography scanning
InactiveUS7356112B2Effect can be studiedContinuous acquisitionImage enhancementReconstruction from projectionProjection imageTherapeutic radiation
Artifacts in the reconstructed volume data of cone beam CT systems can be removed by the application of respiration correlation techniques to the acquired projection images. To achieve this, the phase of the patients breathing is monitored while acquiring projection images continuously. On completion of the acquisition, projection images that have comparable breathing phases can be selected from the complete set, and these are used to reconstruct the volume data using similar techniques to those of conventional CT. Any phase can be selected and therefore the effect of breathing can be studied. It is also possible to use a feature in the projection images such as the patient's diaphragm to determine the breathing phase. This feature in the projection images can be used to control delivery of therapeutic radiation dependent on the patient's breathing cycle, to ensure that the tumor is in the correct position when the radiation is delivered.
Owner:ELEKTA AB
X-ray imaging system and x-ray imaging method
InactiveUS20120051498A1Reduce exposureReduced imaging timeReconstruction from projectionMaterial analysis using wave/particle radiationX-rayX ray image
An X-ray imaging system is for irradiating a subject with X ray from an X-ray source at a plurality of different angles to acquire X-ray images, and reconstructing an X-ray tomographic image from the X-ray images. The system comprising a region setting unit for setting a region of interest on a pre-shot image or a previously acquired X-ray tomographic image, an imaging control unit for continuously varying an aperture formed by collimator blades according to a position of the X-ray source to image the region of interest and acquiring projection data of the X-ray images in accordance with the position of the X-ray source, and an image reconstructing unit for reconstructing the X-ray tomographic image from the projection data of the X-ray images of the region of interest. The aperture formed by the collimator blades are varied so that all the X-ray images formed on the X-ray detector is rectangular regardless of the position of the X-ray source.
Owner:FUJIFILM CORP
Radiation imaging device
InactiveUS8787520B2Promote generationHigh degreeReconstruction from projectionMaterial analysis using wave/particle radiationSoft x rayImaging quality
Owner:HITACHI LTD
Computer tomography imaging device and method
ActiveUS9380984B2Increase speedReduce hardware costsReconstruction from projectionMaterial analysis using wave/particle radiationX-rayTomography
The present invention discloses a method for performing CT imaging on a region of interest of an object under examination, comprising: acquiring the CT projection data of the region of interest; acquiring the CT projection data of region B; selecting a group of PI line segments covering the region of interest, and calculating the reconstruction image value for each PI line segment in the group; and combining the reconstruction image values in all the PI line segments to obtain the image of the region of interest. The present invention further discloses a CT imaging device using this method and a data processor therein. Since the 2D / 3D slice image of the region of interest can be exactly reconstructed and obtained as long as the X-ray beam covers the region of interest and the region B, it is possible to use a small-sized detector to perform CT imaging on the region of interest at any position of a large-sized object, which reduces to a great extent the radiation dose of the X-ray during the CT scanning.
Owner:TSINGHUA UNIV +1
Method and system for simultaneously viewing rendered volumes
InactiveUS20050135555A1Reduce artifactsReconstruction from projectionMaterial analysis using wave/particle radiationViewpointsComputer graphics (images)
A technique is provided for concurrently viewing volumes that may be rendered using visualization techniques incorporating one or more functions, such as depth-dependent weighting functions. In one aspect, the viewing technique may provide for the concurrent viewing of volumes, such as overlapping volumes, from different viewpoints. In accordance with this aspect, the relative position of display may convey the relative viewpoints. In addition, the viewing technique may provide for concurrently displaying volume renderings of a volume in which the volume renderings are generated using different functions, such as weighting and / or transfer functions. In this manner, the effect of the functions on visual properties of structures within the volume may be observed.
Owner:GENERAL ELECTRIC CO
Method and apparatus for increasing field of view in cone-beam computerized tomography acquisition
ActiveUS9795354B2Cost of component being equalIncrease in sizeReconstruction from projectionRadiation diagnostic device controlTomographyField of view
A method and apparatus for Cone-Beam Computerized Tomography, (CBCT) is configured to increase the maximum Field-Of-View (FOV) through a composite scanning protocol and includes acquisition and reconstruction of multiple volumes related to partially overlapping different anatomic areas, and the subsequent stitching of those volumes, thereby obtaining, as a final result, a single final volume having dimensions larger than those otherwise provided by the geometry of the acquisition system.
Owner:CEFLA SOC COOP
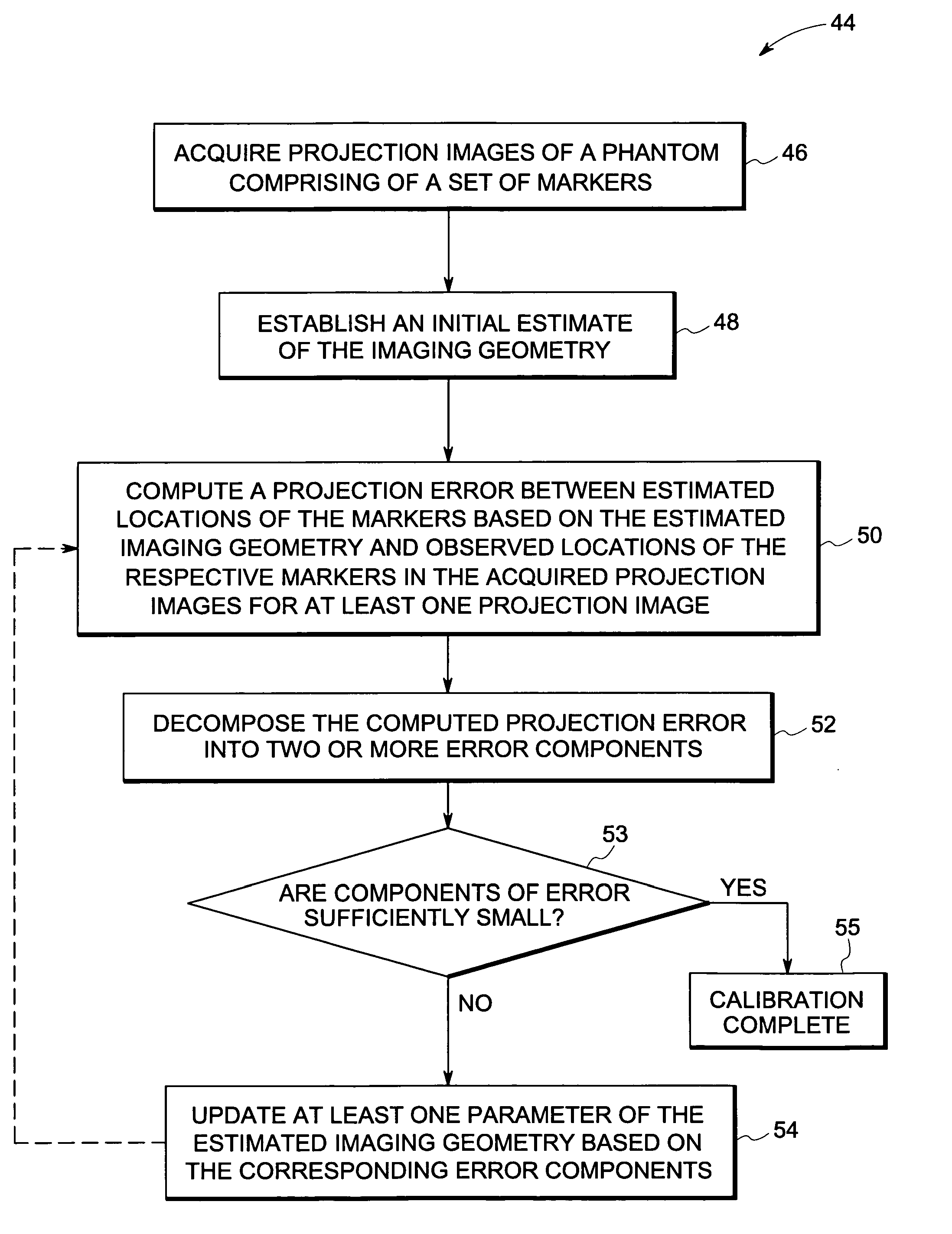
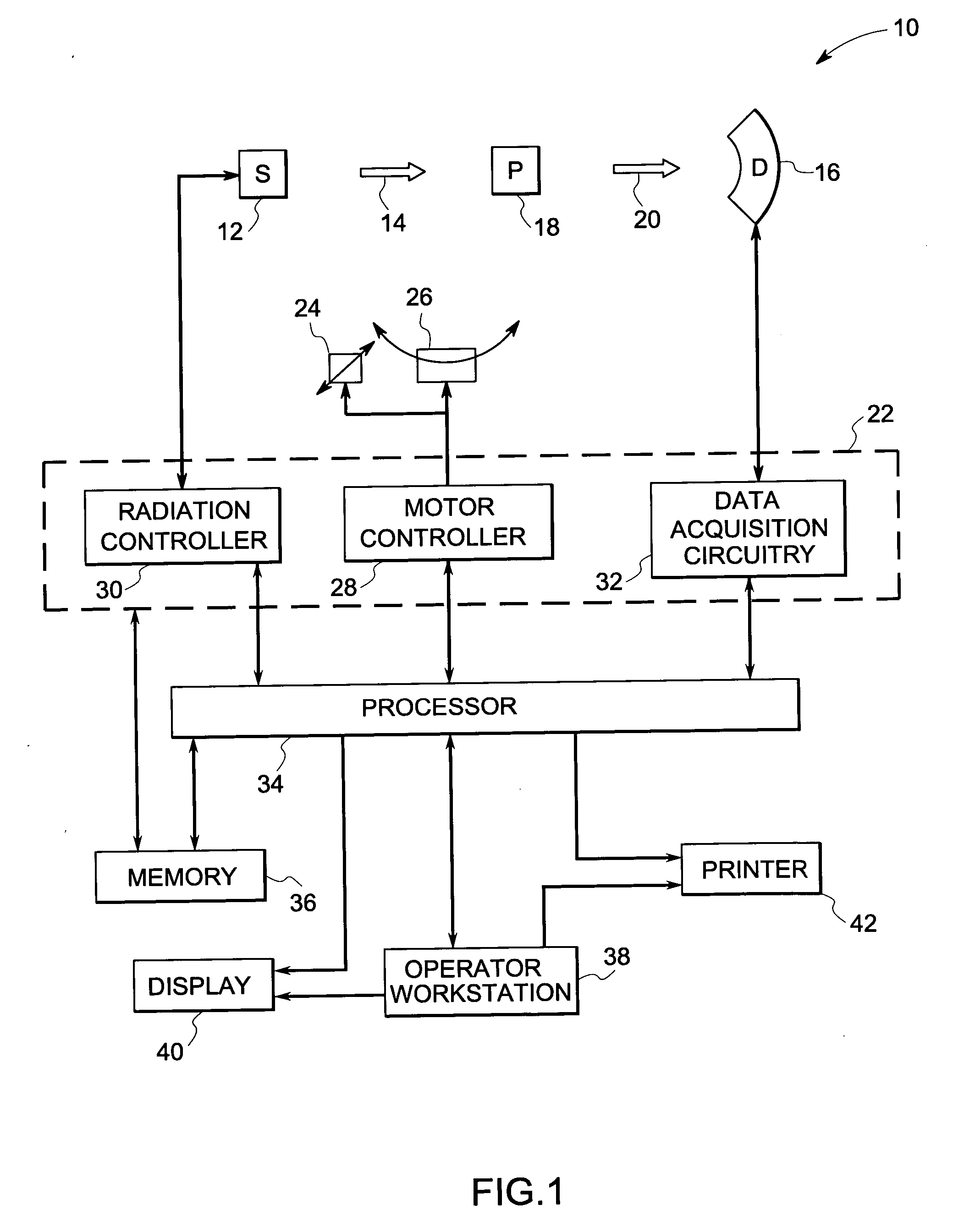
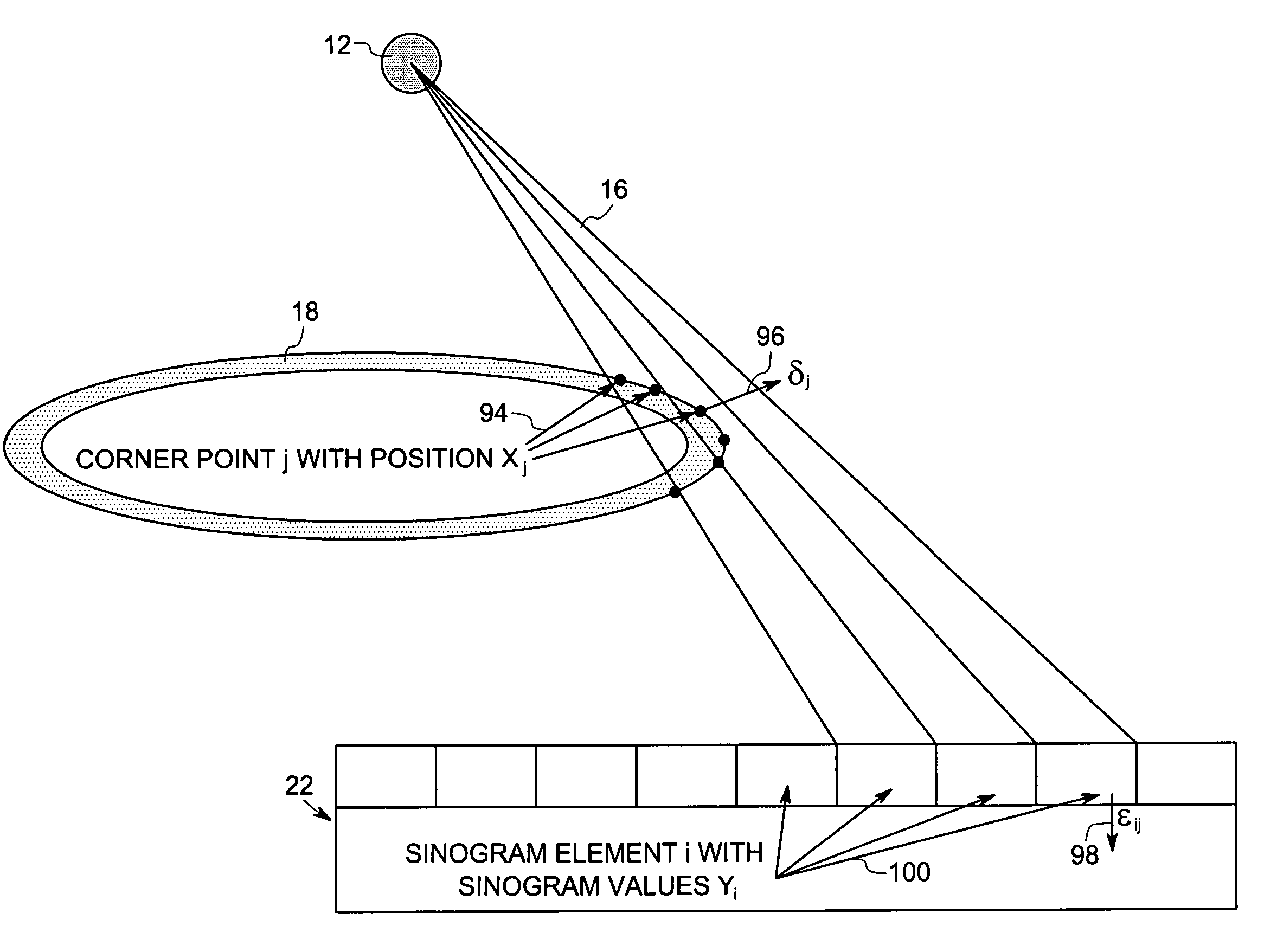
Method and device for geometry analysis and calibration of volumetric imaging systems
ActiveUS20070122020A1Enhance the imageImprove accuracyReconstruction from projectionMaterial analysis using wave/particle radiationVolumetric imagingProjection image
A technique is provided for geometrical analysis and calibration of a volumetric imaging system. The technique includes computing a projection error between estimated locations of a set of markers of a phantom based on a estimated imaging geometry and observed locations of the respective markers for at least one projection image, decomposing the computed projection error into one or more error components corresponding to respective geometric parameters of the imaging geometry, and updating at least one parameter of the estimated imaging geometry based on the one or more error components.
Owner:GENERAL ELECTRIC CO
Method and apparatus for compressed sensing
ActiveUS20060029279A1Reduce in quantityImage enhancementReconstruction from projectionM-matrixCompressed sensing
The invention provides a method and apparatus for making reduced numbers of measurements compared to current practice and still give acceptable quality reconstructions of the object of interest. In one embodiment, a digital signal or image is approximated using significantly fewer measurements than with traditional measurement schemes. A component x of the signal or image can be represented as a vector with m entries; traditional approaches would make m measurements to determine the m entries. The disclosed technique makes measurements y comprising a vector with only n entries, where n is less than m. From these n measurements, the disclosed invention delivers an approximate reconstruction of the m-vector x. In another embodiment, special measurement matrices called CS-matrices are designed for use in connection with the embodiment described above. Such measurement matrices are designed for use in settings where sensors can allow measurements y which can be represented as y=Ax+z, with y the measured m-vector, x the desired n-vector and z an m-vector representing noise. Here, A is an n by m matrix, i.e. an array with fewer rows than columns. A technique is disclosed to design matrices A which support delivery of an approximate reconstruction of the m-vector x, described above. Another embodiment of the invention discloses approximate reconstruction of the vector x from the reduced-dimensionality measurement y within the context of the embodiment described above. Given the measurements y, and the CS matrix A, the invention delivers an approximate reconstruction x# of the desired signal x. This embodiment is driven by the goal of promoting the approximate sparsity of x#.
Owner:THE BOARD OF TRUSTEES OF THE LELAND STANFORD JUNIOR UNIV
System For The Three-Dimensional Imaging Of A Moving Joint
InactiveUS20080094396A1Highly informativeHigh analysisReconstruction from projectionCharacter and pattern recognition3d imageX-ray
The invention relates to a system and a method for the generation of 3D images of a moving joint (1). A rotational X-ray device (10) generates projections of said joint from different directions while the simultaneous periodic movement of the joint (1) is recorded by a monitoring device (20). The generated X-ray projections are then classified according to the phase of joint movement to which they belong, and 3D images are reconstructed from X-ray projections of each class. Thus a 3D movie of the joint movement can be produced and shown on a monitor. The monitoring device (20) may particularly be realized by an apparatus that allows the forced movement of the joint (1) in synchronization with the generation of X-ray projections.
Owner:KONINKLIJKE PHILIPS ELECTRONICS NV
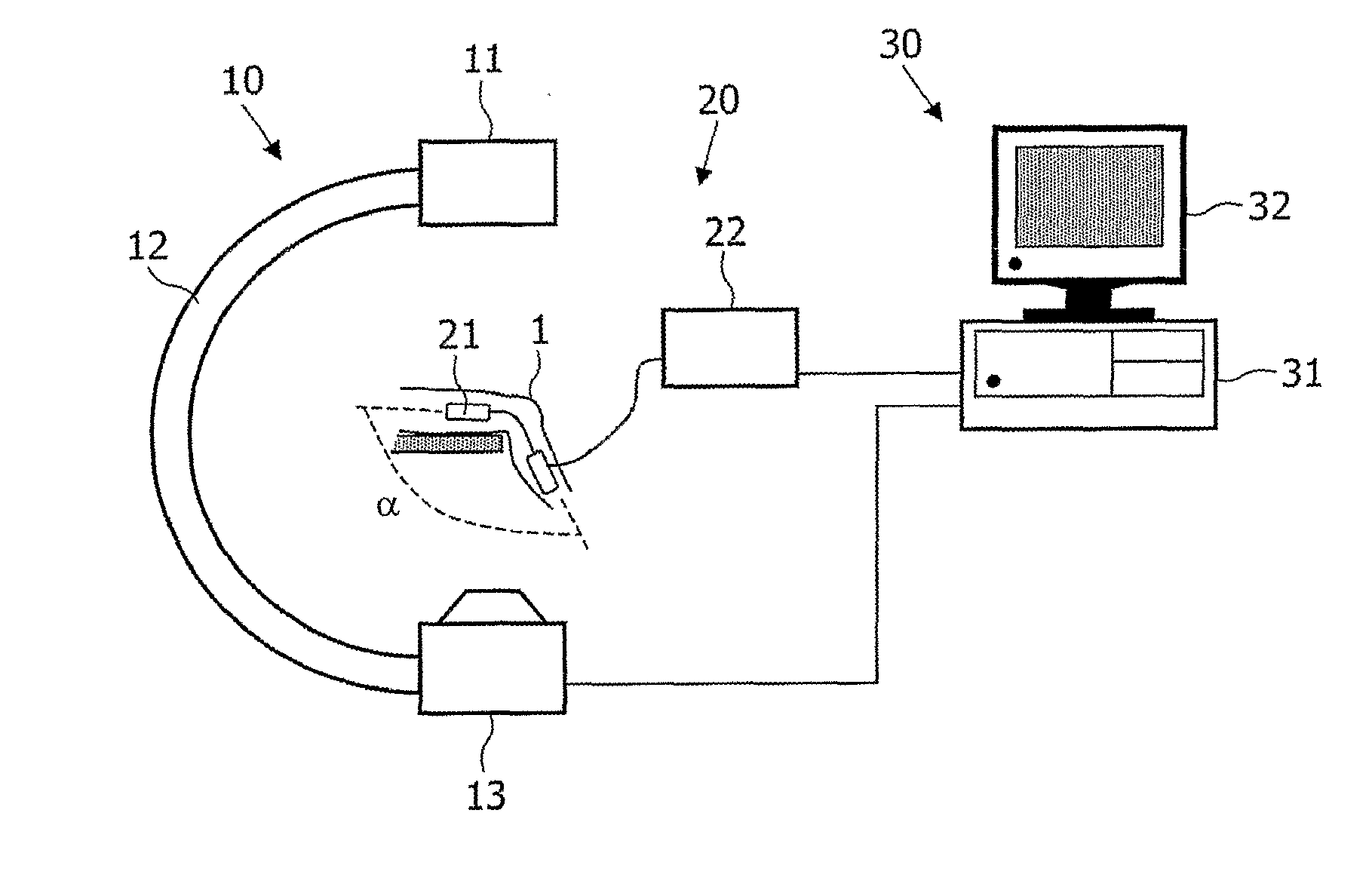
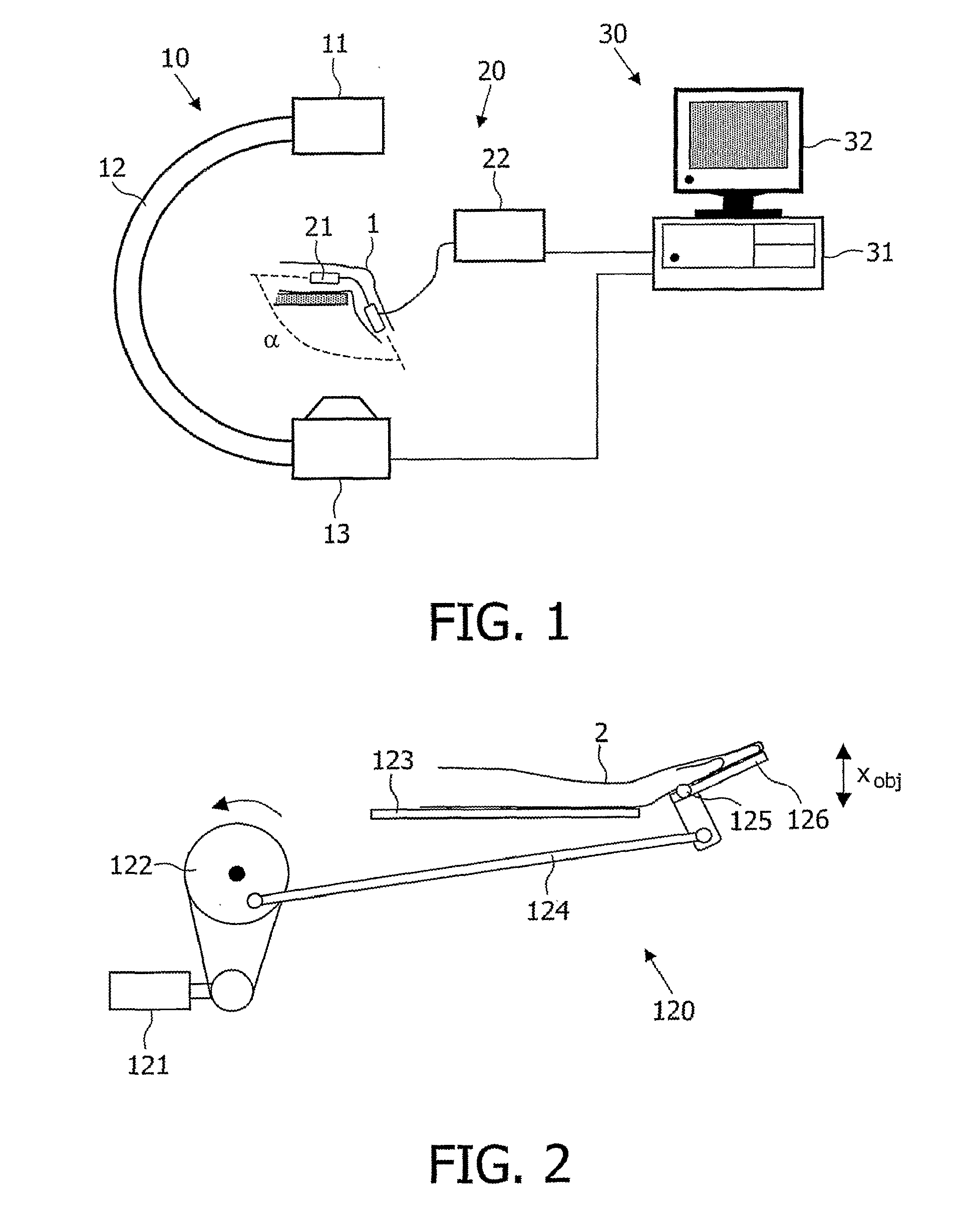
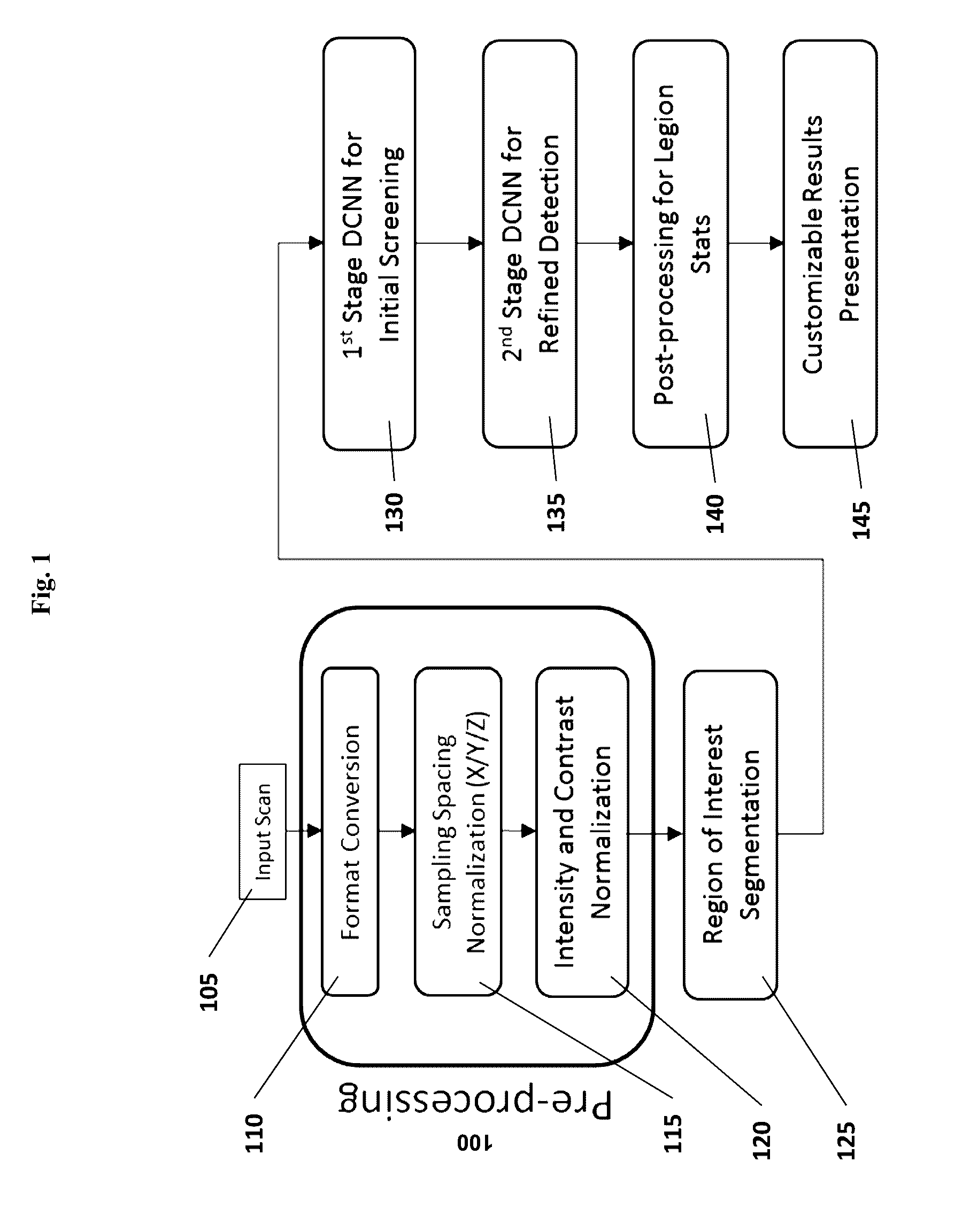
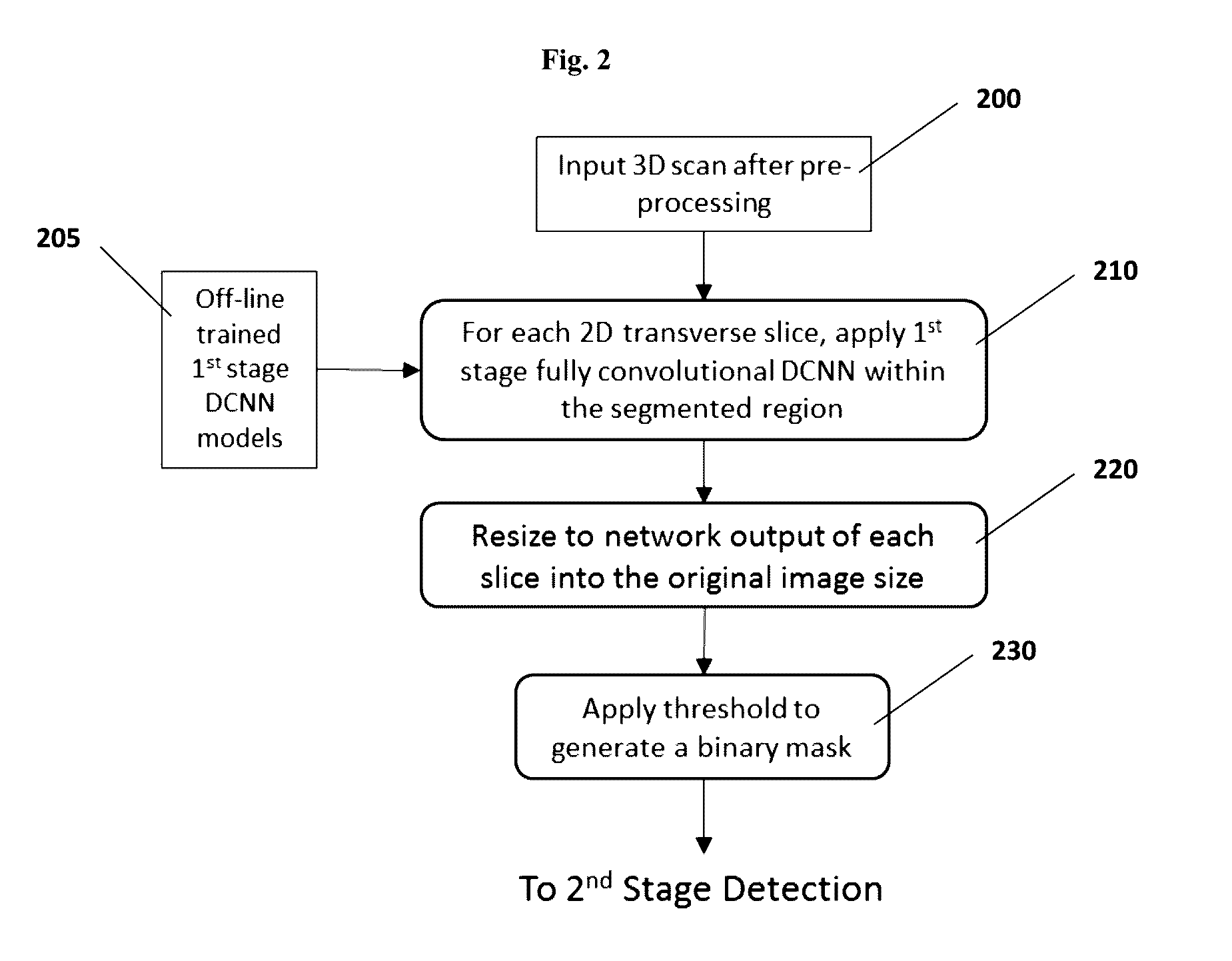
Computer-aided diagnosis system for medical images using deep convolutional neural networks
InactiveUS9589374B1Examination time can be shortenedImprove diagnostic accuracyUltrasonic/sonic/infrasonic diagnosticsImage enhancementComputer visionAided diagnosis
Owner:12 SIGMA TECH
Image handling and display in X-ray mammography and tomosynthesis
Owner:HOLOGIC INC
System and method for three-dimensional image rendering and analysis
InactiveUS7274810B2Reduce decreaseReduce contributionImage enhancementReconstruction from projectionComputer visionImage analysis
The present invention relates to methods and systems for conducting three-dimensional image analysis and diagnosis and possible treatment relating thereto. The invention includes methods of handling signals containing information (data) relating to three-dimensional representation of objects scanned by a scanning medium. The invention also includes methods of making and analyzing volumetric measurements and changes in volumetric measurements which can be used for the purpose of diagnosis and treatment.
Owner:CORNELL RES FOUNDATION INC +1
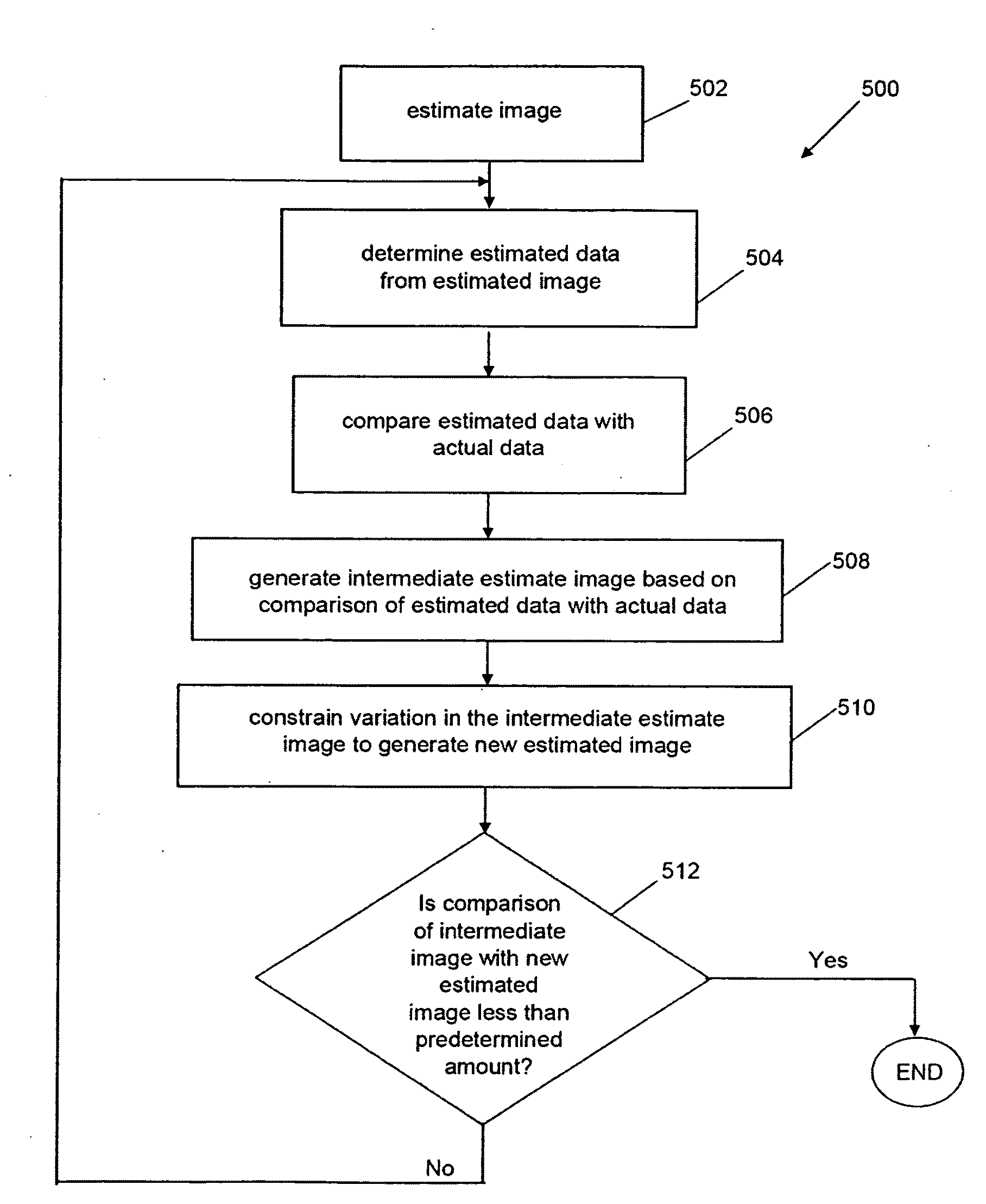
Image Reconstruction From Limited or Incomplete Data
ActiveUS20110044546A1Lessen and reducing total variationReconstruction from projectionCharacter and pattern recognitionComplete dataComputer vision
A system and method are provided for reconstructing images from limited or incomplete data, such as few view data or limited angle data or truncated data (including exterior and interior data) generated from divergent beams. In one aspect of the invention, the method and apparatus iteratively constrains the variation of an estimated image in order to reconstruct the image. As one example, a divergent beam maybe used to generate data (“actual data”). As discussed above, the actual data may be less than sufficient to exactly reconstruct the image by conventional techniques, such as FBP. In order to reconstruct an image, a first estimated image may be generated. Estimated data may be generated from the first estimated image, and compared with the actual data. The comparison of the estimated data with the actual data may include determining a difference between the estimated and actual data. The comparison may then be used to generate a new estimated image. For example, the first estimated image may be combined with an image generated from the difference data to generate a new estimated image. In order to generate the image for the next iteration, the variation of the new estimated image may be constrained. For example, the variation of the new estimated image may be at least partly constrained in order to lessen or reducing the total variation of the image.
Owner:UNIVERSITY OF CHICAGO
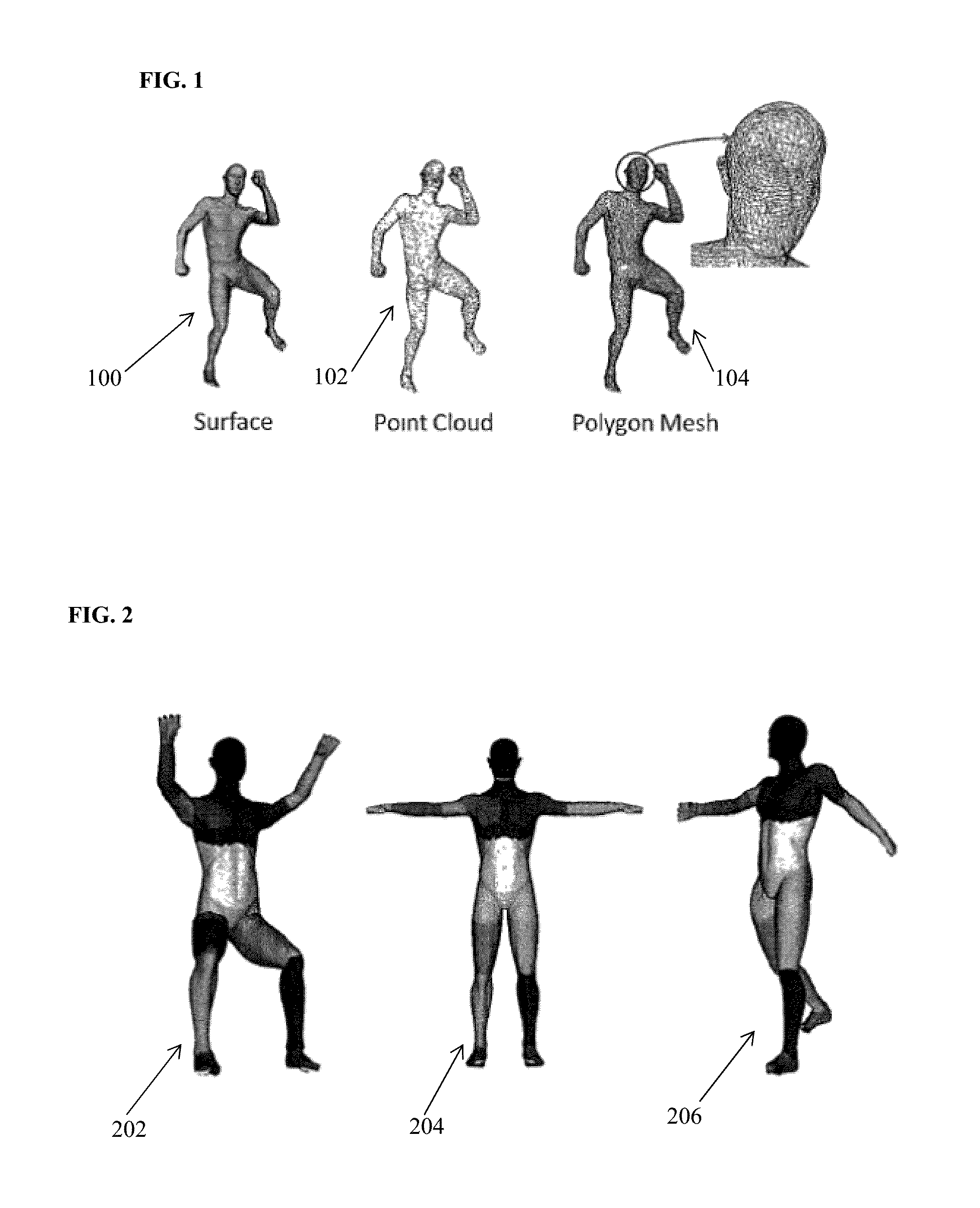
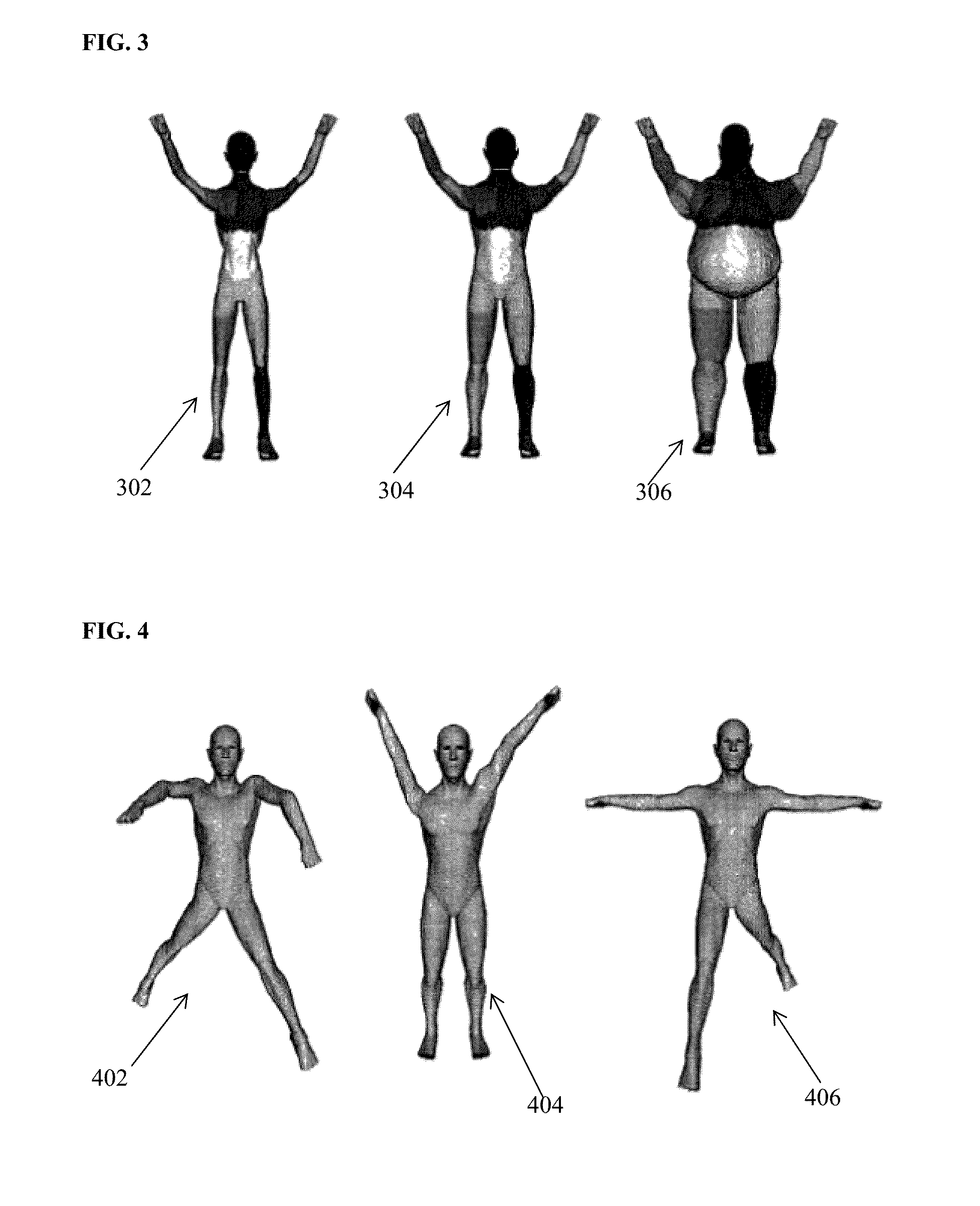
Method and System for Constructing Personalized Avatars Using a Parameterized Deformable Mesh
A method and apparatus for generating a 3D personalized mesh of a person from a depth camera image for medical imaging scan planning is disclosed. A depth camera image of a subject is converted to a 3D point cloud. A plurality of anatomical landmarks are detected in the 3D point cloud. A 3D avatar mesh is initialized by aligning a template mesh to the 3D point cloud based on the detected anatomical landmarks. A personalized 3D avatar mesh of the subject is generated by optimizing the 3D avatar mesh using a trained parametric deformable model (PDM). The optimization is subject to constraints that take into account clothing worn by the subject and the presence of a table on which the subject in lying.
Owner:SIEMENS HEALTHCARE GMBH
Method and apparatus for pseudo-projection formation for optical tomography
ActiveUS7738945B2Reconstruction from projectionMaterial analysis using wave/particle radiationMultiple perspectiveOptical tomography
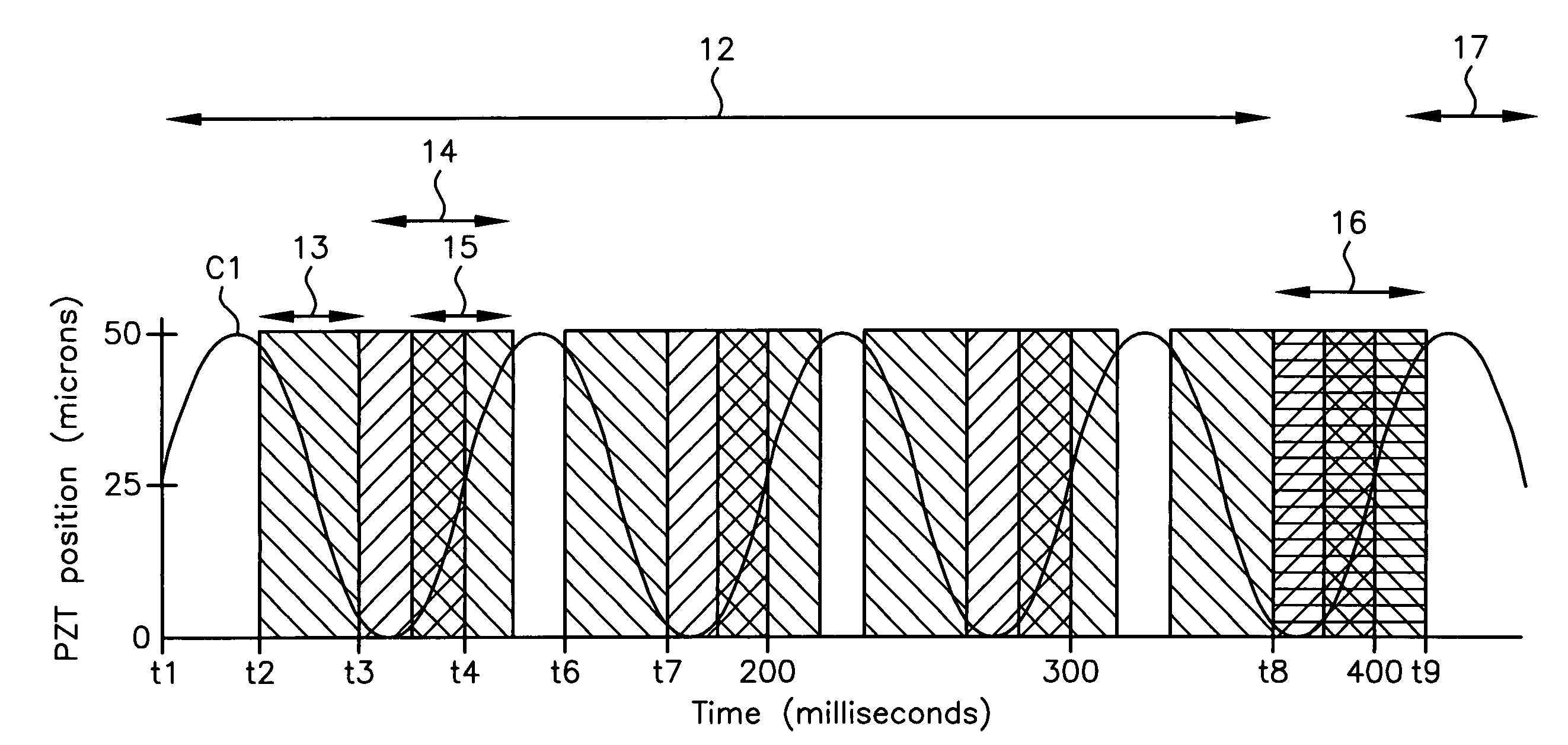
A system for optical imaging of a thick specimen that permits rapid acquisition of data necessary for tomographic reconstruction of the three-dimensional (3D) image. One method involves the scanning of the focal plane of an imaging system and integrating the range of focal planes onto a detector. The focal plane of an optical imaging system is scanned along the axis perpendicular to said plane through the thickness of a specimen during a single detector exposure. Secondly, methods for reducing light scatter when using illumination point sources are presented. Both approaches yield shadowgrams. This process is repeated from multiple perspectives, either in series using a single illumination / detection subsystem, or in parallel using several illumination / detection subsystems. A set of pseudo-projections is generated, which are input to a three dimensional tomographic image reconstruction algorithm.
Owner:UNIV OF WASHINGTON +1
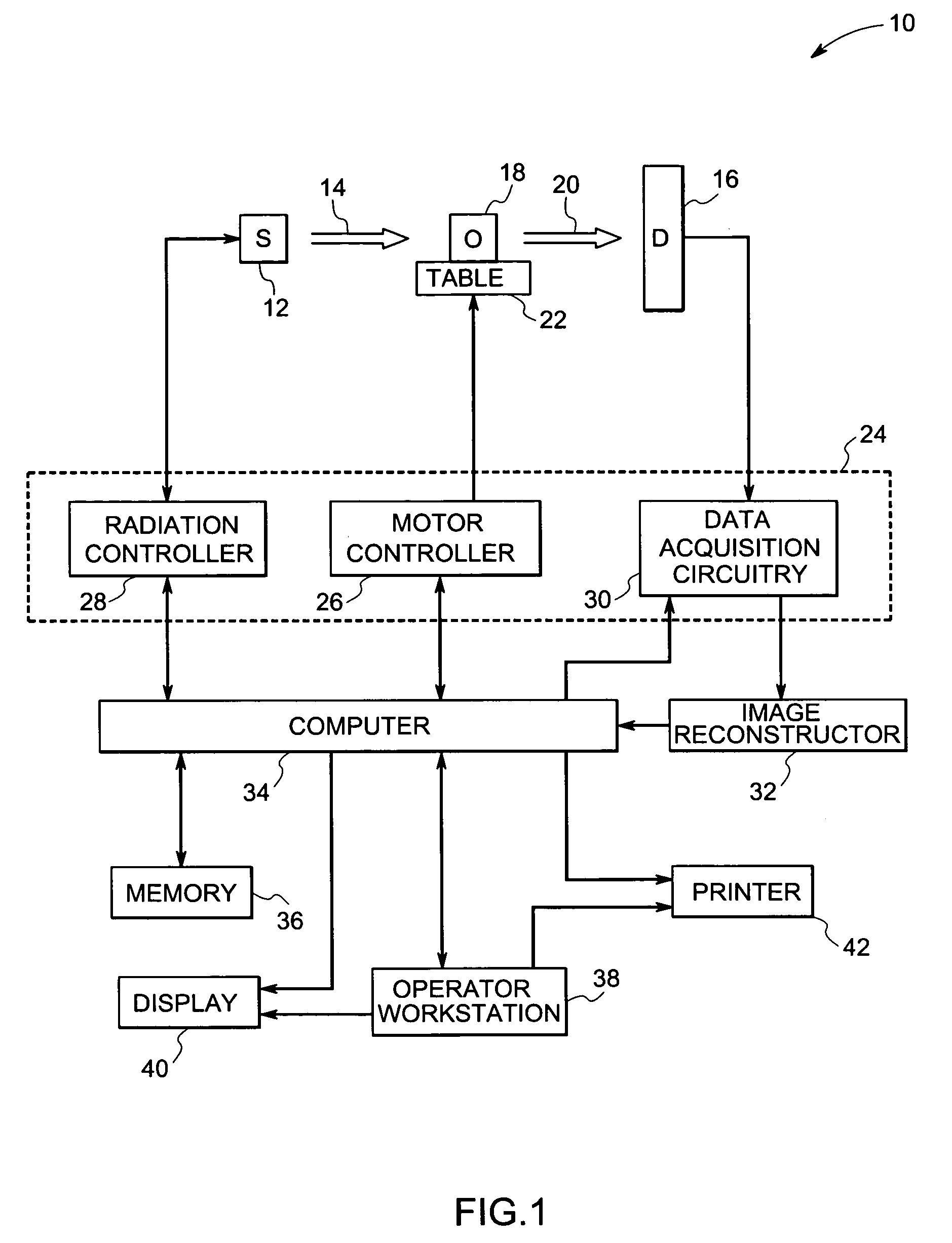
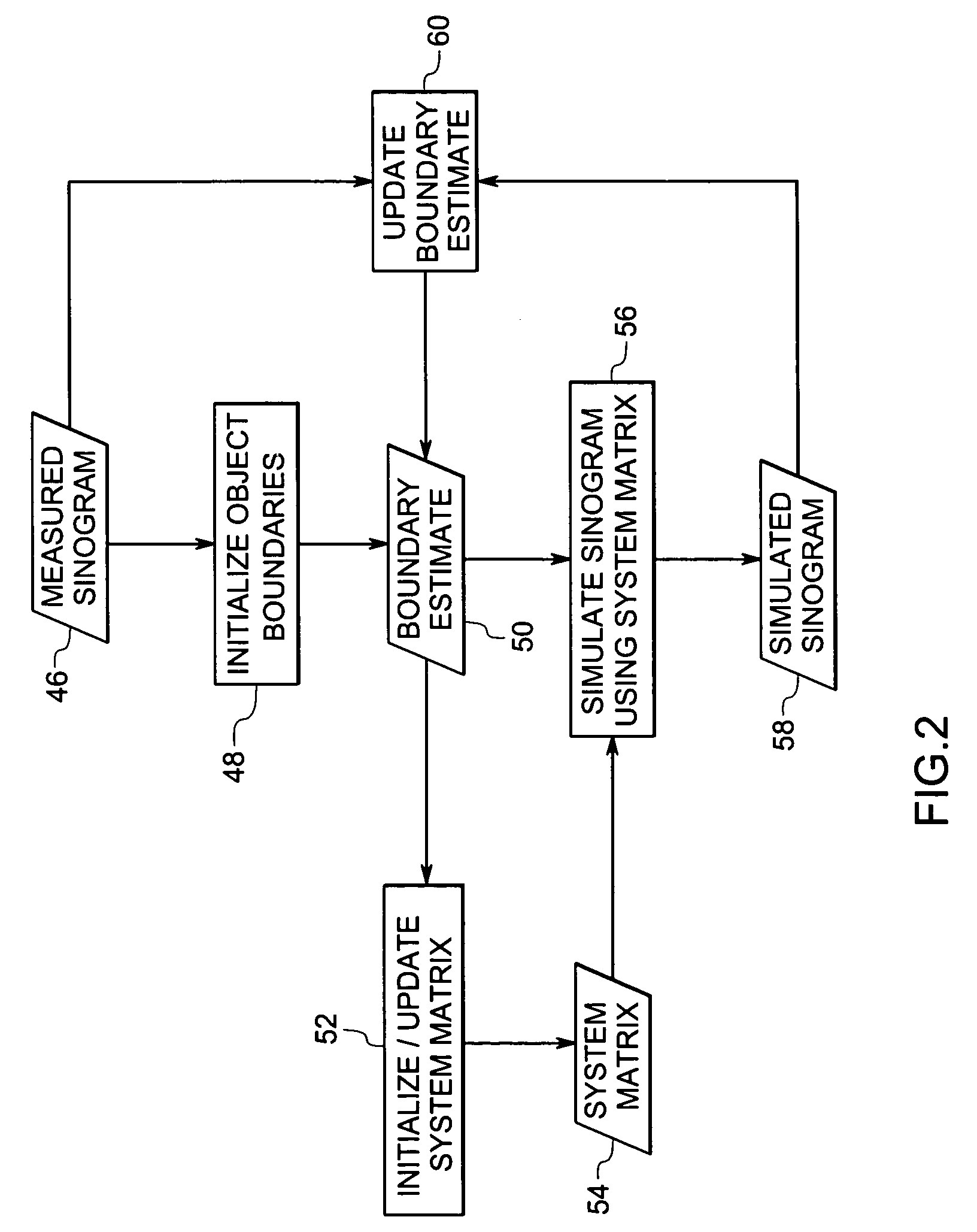
System and method for boundary estimation using CT metrology
InactiveUS7203267B2Reconstruction from projectionMaterial analysis using wave/particle radiationMetrologyAlgorithm
A technique is provided for CT reconstruction for use in CT metrology. The boundary based CT reconstruction method includes the steps of initializing a boundary of an object to obtain a boundary estimate, defining a forward model based on the boundary estimate, linearizing the forward model to obtain a system matrix and implementing an iterative image reconstruction process using the system matrix to update the boundary estimate.
Owner:GENERAL ELECTRIC CO
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com