System and method for projection lithography with immersed image-aligned diffractive element

Abstract

A novel system and method and computer program product for exposing a photoresist film with patterns of finer resolution than can physically be projected onto the film in an ordinary image formed at the same wavelength. A hologram structure containing a set of resolvable spatial frequencies is first formed above the photoresist film. If necessary the photoresist is then sensitized. An illuminating wavefront containing a second set of resolvable spatial frequencies is projected through the hologram, forming a new set of transmitted spatial frequencies that expose the photoresist. The transmitted spatial frequencies include sum frequencies of higher frequency than is present in the hologram or illuminating wavefront, increasing the resolution of the exposing pattern. These high spatial frequency transmitted waves can be evanescent, or they can propagate at a steeper obliquity in a higher index medium than is possible in a projected image. A further method is described for designing lithographic masks to fabricate the hologram and to project the illuminating wavefront. In other embodiments, a simple personalization based on Talbot fringes and plasmonic interference is performed.

Description

BACKGROUND OF THE INVENTION[0001]1. Field of the Invention[0002]The present invention relates generally to lithographic formation of integrated circuit patterns, and more particularly to a method for generating the spatial frequency modulation of a lithographic pattern by projecting a light beam that has been modulated with a set of spatial frequencies through a hologram modulated by a signal having a second spatial frequency modulation.[0003]2. Description of the Prior Art[0004]The resolution of a lithographic image is limited by the wavelength of the light that forms it. Currently, source wavelengths shorter than λ=193 nm (e.g., as provided by an ArF excimer light source) are not contemplated for IC manufacture until the future era of soft x-ray lithography. Fortunately, wavelength is reduced inside a medium, and a favorable reduction of as much as 1.8× can potentially be obtained for propagating waves within photoresist films. This corresponds to an upper limit of 1.8 for the res...

AI Technical Summary

Benefits of technology

[0039]Further to this aspect, the lithographic method further includes: inhibiting the photosensitive medium layer from exposure during forming of the diffractive hologram structure; and, switching on sensitivity of the photosensitive medium layer after forming the diffractive hologram structure. In one embodiment, avoiding premature exposure of the primary photosensitive layer includes giving the hologram formation layer a much higher sensitivity.

[0057]In each of these embodiments of the invention, the mask design method employs an electromagnetic optimizer when iterating between steps d)-e), the optimizer maximizing lithographic process window utilization and, maximizing a range of light dose and focus fluctuations within which the bright and dark polarity patterns in the developed image match the target patterns to within an acceptable tolerance.

Problems solved by technology

The resolution of a lithographic image is limited by the wavelength of the light that forms it.

However, evanescent waves can only exist in extremely thin films, and even the somewhat larger thicknesses that are typically given to photoresist films (of order 0.1-1.0 microns) are microscopic on the scale of the lens elements which propagate the light from mask to wafer.

The macroscopic size of conventional projection lenses makes them unsuitable for exploiting waves that become evanescent in any medium between the resist film stack and the mask.

In fact, until recently, lithographic projection lenses were incapable of introducing spatial frequencies into the image that corresponded to wavelengths shorter than the vacuum wavelength.

Increasing the refractive index of the immersion fluid is challenging with a 193 nm source wavelength, because high index fluids tend to have high absorption in the deep UV.

Moreover, the lens elements in 193 nm systems also face stringent materials requirements, and their refractive index is currently limited to n=1.56 or below.

This is because the final lens element generally cannot have a concave exit surface since the immersion cavity would then become impractically thick along the optical axis, greatly stiffening the already difficult-to-surmount materials requirements that a hypothetical high-index immersion fluid must meet.

In fact, it is currently believed that the materials challenges involved in significantly raising the refractive index of the final lens element are at least as difficult as those faced in raising the index of the coupling medium.

Achieving the necessary freedom from minute levels of index in-homogeneity and uncorrectable birefringence is extremely difficult at 193 nm, given the element sizes and tolerance levels needed for advanced lithography lenses.

Thus, with existing methods of projection lithography the spatial frequency content of the projected image ends up being gated by an effective wavelength of about λ / 1.35, potentially limiting the miniaturization of future semiconductor designs.

Unfortunately, even with one dimensional (1D) layouts, the tight transfer process control needed to print a narrow feature from a wide image will usually prevent a doubling of minimum manufacturable resolution from being feasible by this means—resolution improvements are typically quite a bit less than 2×.

Even under ideal conditions, achievement of more than a doubling of resolution would require three or more transfer steps, which would cause cost to rise very substantially.

Note that with two-dimensional (2D) patterns, a fill doubling of resolution in every cross-section (e.g. along both the x and y axes) is not even theoretically possible if only two exposures are used.

However, this classic approach is inherently unable to provide more than a single doubling of resolution.

One drawback to Talbot lithography is that the printed features are restricted to periodic line / space patterns.

While there is a significant subset of semiconductor devices whose design layouts are relatively simple (and moreover such devices may be of particular importance at the ultra-high resolutions where difficulties in device scaling make large and complex circuit layouts more problematic), pure line / space patterns are only of limited utility.

A second difficulty arises in fabricating the parent grating.

Some of the state-of-the-art techniques described above can provide such fine resolutions, which can then be reduced further through Talbot lithography; however such spatial frequencies for the parent grating fall near the limit of current lithographic technology, and can prove difficult to manufacture.

A more fundamental difficulty is that future semiconductor technologies will require printing pitches that are considerably smaller than the wavelength, and under such circumstances electromagnetic effects due to interaction of the incident light with the resist topography produces an undesired increase of the energy diffracted into the 0th order, hence critically degrading the double-frequency Talbot image in this regime.

For this reason a standard grating structure will generally be unable to provide the sub-wavelength frequency-doubled fringe pattern that is needed to achieve a resolution superior to current projection technology.

In this technique, complex electromagnetic effects also arise when light is transmitted through grating arrays (1D or 2D) of pinholes or slits in metallic films, particularly metals whose dielectric constant has a large negative real part.

Thus far only gratings have been proposed for plasmonic lithography, limiting this technique to very specialized applications.

And, as with Talbot parent gratings for sub-wavelength spatial frequencies, analysis of the plasmonic gratings is numerically intensive.

A significant problem with the solid immersion approach however, is that large-NA projection systems can only be optically corrected to the diffraction limit over fields that are quite small; typically somewhat smaller than a single chip, and far smaller than a silicon wafer.

Unfortunately, a microscopic liquid layer prevents relative motion between the lens and wafer, and it cannot be rapidly applied or released.

Solid immersion lithography is relatively impractical, and can only be expected to extend the spatial frequency limit of projection systems by a small margin since the refractive index of the final lens element that is contacted to the resist stack is currently limited to n=1.56 or below.

Talbot lithography is relatively inflexible in the patterns it can produce, and it cannot easily provide high contrast frequency doubling as feature sizes become strongly sub-wavelength, due to EMF enhancement of the zero order at these dimensions.

However, such a lens element (alternately referred to as a diffractive or holographic element) is not suitable as a final contacted lens surface in a lithographic system that seeks to overcome the limitations imposed by the refractive index of the exit space by placing the final element in close proximity to the wafer.

In a conventional configuration, the holographic element can be spaced away from the image field and given a larger diameter, but this is not possible in a solid immersion system where materials limitations force the high index space between the hologram and image to be quite thin.

A related problem is that the aberrations in a Fresnel lens of such high power would be impossible to correct in a telecentric system.

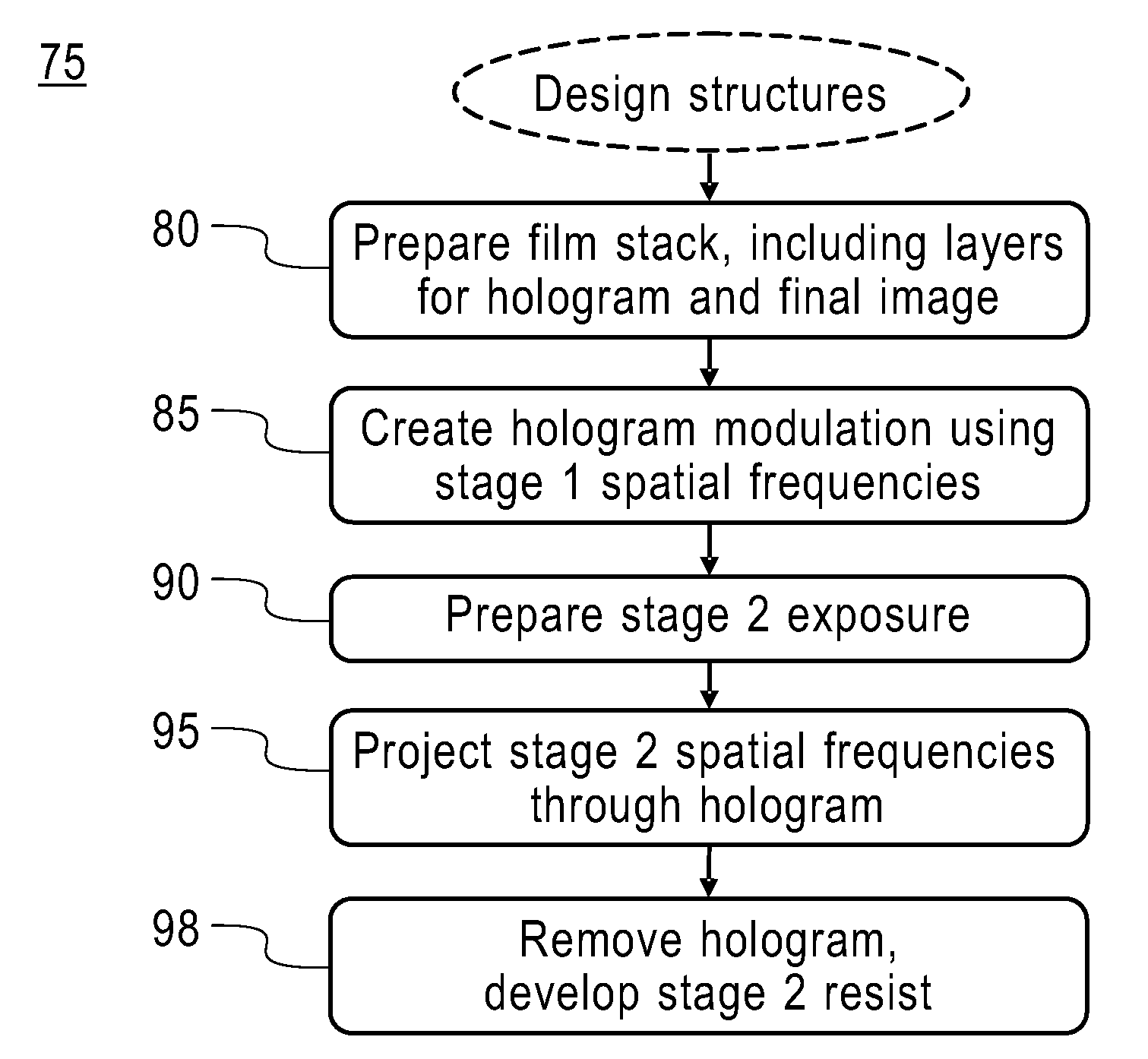
The drawback to such a holographic approach is that the problem of fabricating an ultra-high-resolution image is simply re-posed as that of fabricating the hologram.

For this reason, the conventional holograms do not offer the desired path to improved resolution, since the resolution needed to fabricate them is in general no coarser than the resolution attainable in the diffracted patterns that they can form.

Images