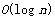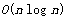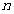Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Construction method of dynamic spatial space index for supporting STL data source

A technology of spatial indexing and construction method, applied in electrical digital data processing, special data processing applications, instruments, etc., can solve the problems of lack of patch adjacency information, grid vertex data redundancy, etc., to improve reconstruction efficiency and support fast The effect of query and removal efficiency improvement

Inactive Publication Date: 2015-08-26
SHANDONG UNIV OF TECH
View PDF2 Cites 6 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to propose an explicit surface topology reconstruction algorithm based on a multi-dimensional dynamic spatial index for the defects of grid vertex data redundancy and lack of surface adjacency information in the current STL file format. The redundant vertex data in the STL file is integrated into the half-edge structure based on the openness of the index structure to realize the rapid reconstruction of the mesh surface topology. Quick Search of Topological Neighborhood Information of Lattice Surface

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Construction method of dynamic spatial space index for supporting STL data source
  • Construction method of dynamic spatial space index for supporting STL data source
  • Construction method of dynamic spatial space index for supporting STL data source

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0035] Embodiment 1: construct the KD tree of grid vertex in the process of elimination of vertex data copy, and the time complexity of building the tree is , the space complexity is , the time complexity of the nearest neighbor query is ,in is the number of mesh vertices. from Figure 18 It can be seen from the figure that compared with the time taken to perform nearest neighbor query on all grid vertices by eliminating the vertex data copy, the tree building time is two orders of magnitude smaller. It is about 0.2s, which is almost negligible. The algorithm in this paper uses a three-dimensional dynamic spatial index in the process of judging vertex data replicas, and uses the efficient query performance of the KD tree to perform nearest neighbor query operations on all vertices in the STL file. The total time for removing redundant vertices is the sum of the tree building time and query time . from Figure 19 It can be seen from the figure that this paper uses t...

Embodiment 2

[0036] Embodiment 2: In the surface topology reconstruction process, the time complexity is O (m), where m set for the half H The number of half-edge bars in . Through the grid index constructed in the process of data copy elimination, the outgoing half-edge information in the half-edge structure is added to the leaf nodes of the index structure, using the KD tree k -The nearest neighbor algorithm quickly queries the information of the dual half edge, improves the efficiency of adjacent patch matching, and realizes the rapid topology reconstruction of the mesh surface. from Figure 20 It can be seen from the figure that when the algorithm in this paper processes a model with more than 900,000 facets, the topology reconstruction only takes more than 2s.

Embodiment 3

[0037] Embodiment 3: Two experiments of vertex data duplicate elimination and surface mesh topology reconstruction show that the algorithm in this paper is very efficient in terms of redundant vertex data elimination and mesh surface topology reconstruction. However, for the topology reconstruction of a grid model, in most cases, it only needs to be reconstructed once, and the grid often needs to be denoised, smoothed, streamlined, etc., so the grid surface topology neighborhood query will play a very important role in the follow-up work. The role of the query efficiency will determine the pros and cons of the algorithm to a certain extent. In order to test the performance of the topology neighborhood query of this algorithm, the Figure 12~17 Perform a 1-ring domain query at any point on the mesh surface shown, that is, query all the triangle surface information around the vertex, such as Figure 21 shown. Randomly collect sample points on different grid surfaces to perform...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a construction method of a gridding curved surface dynamic spatial index for supporting a STL data source, and belongs to the field of digital design and manufacturing. The method is characterized by comprising the following steps: constructing a KD tree index of a gridding curved surface vertex for a digital model in a STL file format, gradually eliminating vertex redundant data in the gridding curved surface in the construction process; fast querying vertex information in the STL data source through the nearest neighbor query algorithm of a KD tree, and improving vertex data duplicate elimination efficiency; integrating into a half-edge data structure based on the openness of KD tree leaf node layer data storage; connecting an adjacent triangular patch through the half-edge ring order and dual half-edge information in the half-edge structure to realize the fast reconstruction of a complete curved surface topological structure. Through the adoption of the integrated dynamic index of the KD tree and the half-edge structure, the removing time and the topological reconstruction time of the redundant vertex are greatly reduced, and the fast query of the gridding curved surface topological neighborhood information is effectively supported.

Description

technical field [0001] The invention provides a dynamic spatial index construction method supporting STL data sources, which can be used to quickly rebuild the topology structure of a digital model of massive data, and belongs to the field of digital design and manufacture. Background technique [0002] The STL file format is a file format developed by 3D Systems for the stereolithography CAD system to record three-dimensional space surface information in a triangular grid structure. Because of its simple data format and good cross-platform, it has been widely used in Rapid prototyping, CAD / CAM, virtual reality and other fields. [0003] In practical applications, the STL file format has inherent defects such as mesh vertex data redundancy and lack of patch adjacency information. With the gradual popularization of 3D printing technology, the negative impact of these defects has become increasingly prominent. The existing solutions mainly use the reference of vertex data in...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
Inventor 孙殿柱郭洪帅李延瑞聂乐魁
Owner SHANDONG UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com