Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for estimating additive fault size of executing agency of satellite attitude control system through second order Kalman filtering algorithm

A technology for satellite attitude control and actuators, applied in general control systems, control/regulation systems, electrical testing/monitoring, etc., can solve problems that cannot truly reflect the size of flywheel faults

Active Publication Date: 2015-04-29
哈尔滨工大卫星技术有限公司
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The present invention aims to solve the problem that the Kalman filter algorithm modeling in the existing satellite attitude control system cannot truly reflect the size of the fault caused by the flywheel, and proposes a method of using the second-order Kalman filter algorithm to estimate the acceleration of the actuator of the satellite attitude control system. Sexual fault size method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for estimating additive fault size of executing agency of satellite attitude control system through second order Kalman filtering algorithm
  • Method for estimating additive fault size of executing agency of satellite attitude control system through second order Kalman filtering algorithm
  • Method for estimating additive fault size of executing agency of satellite attitude control system through second order Kalman filtering algorithm

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

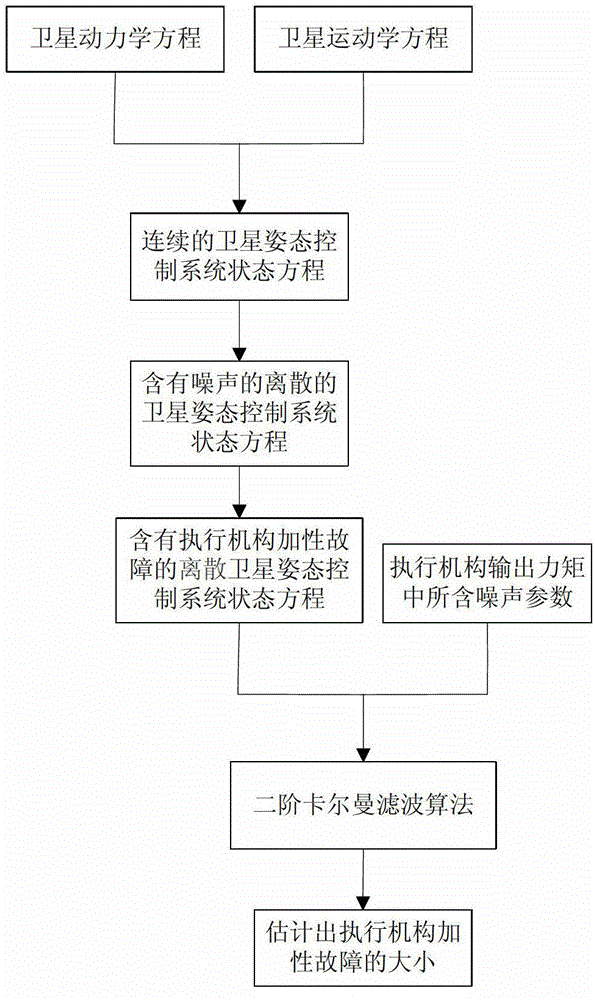
[0018] Specific implementation mode 1: A method for estimating the additive fault size of the actuator of the satellite attitude control system by using the second-order Kalman filter algorithm

[0019] Follow these steps:

[0020] 1. Establish a discrete satellite attitude control system model according to the satellite attitude dynamic equation and kinematic equation;

[0021] 2. For the noise vector w in the discrete satellite attitude control system model k and v k Calibrate during actual operation;

[0022] 3. Establish the mathematical model of the discrete satellite attitude control system with the additive fault of the actuator;

[0023] 4. Analyze the output torque of the actuator and measure the white noise vector in the output torque of the actuator

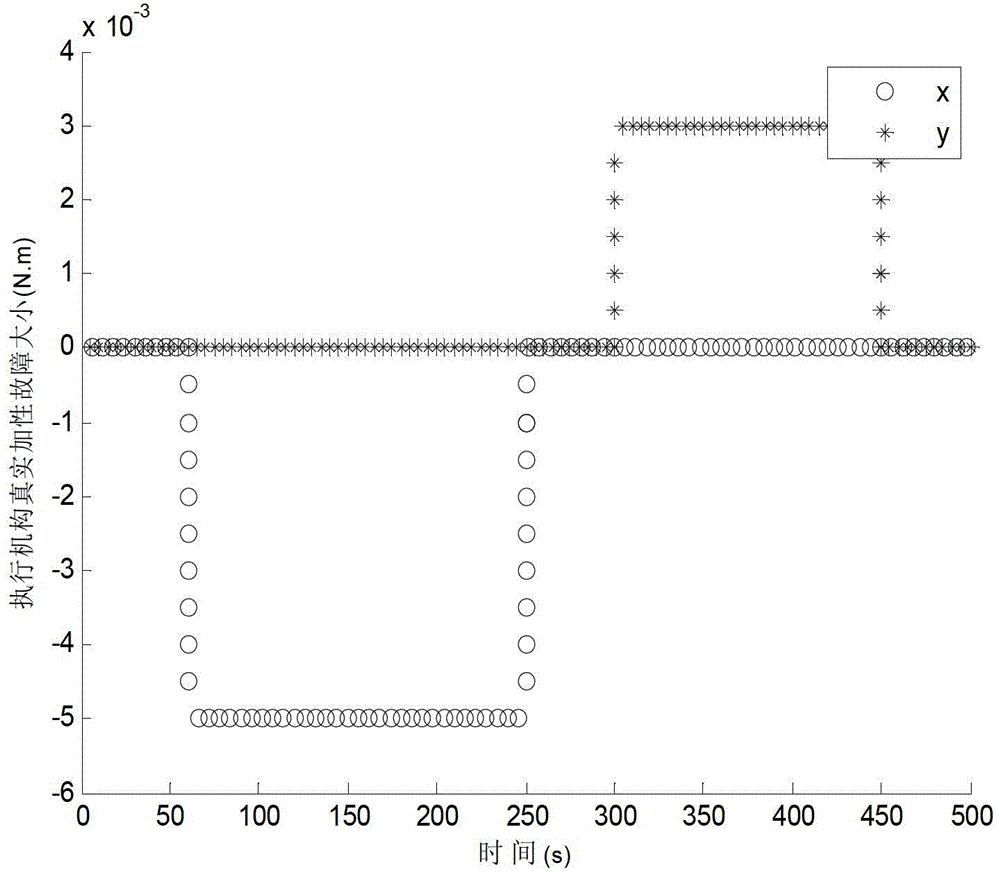
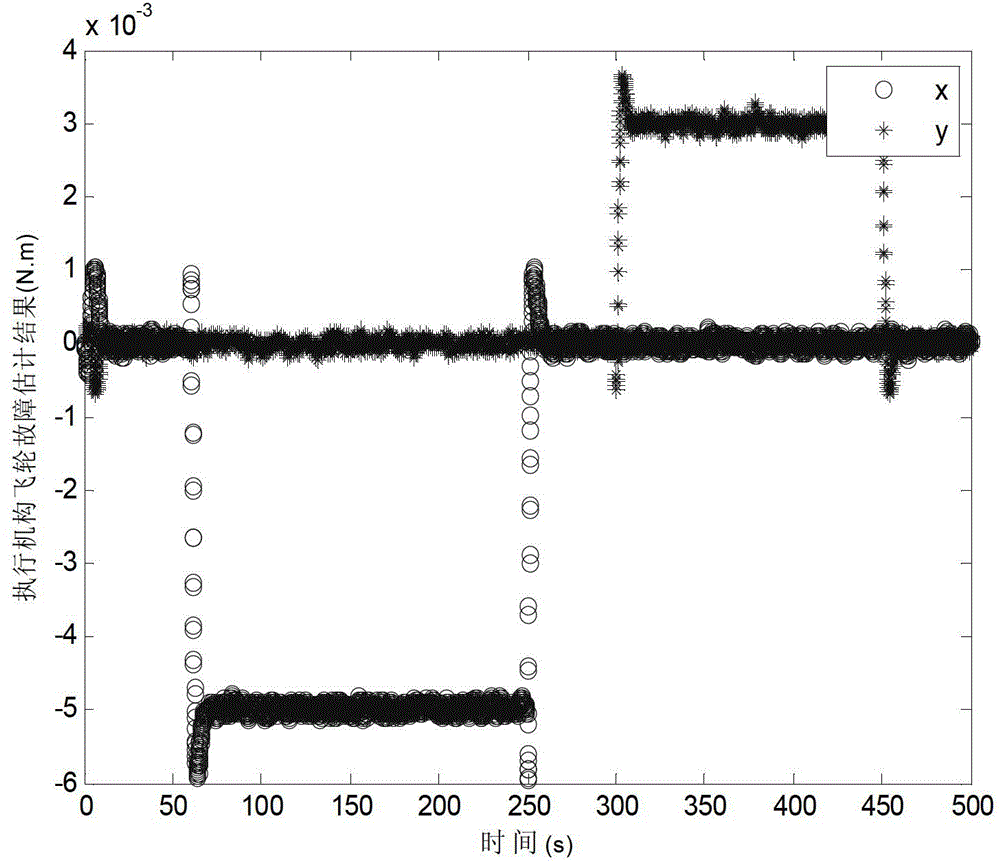
[0024] 5. Transform the above model into the standard form of the second-order Kalman filter algorithm processing model, and use the second-order Kalman filter algorithm to estimate the size of the additive fault...

specific Embodiment approach 2

[0030] Specific implementation mode two: this implementation mode is a further description of specific implementation mode one, and the specific process of step one is:

[0031] 1.1. Establish the state equation of the satellite attitude control system relative to the orbit coordinate system according to the satellite attitude dynamic equation and kinematic equation:

[0032] x · = Ax + Bu y = Cx ;

[0033] where x is the state vector of the state equation of the satellite attitude control system, is the derivative of the state vector of the satellite attitude control system state equation, u is the control input torque vector, y is the output vector; A, B and C are co...

specific Embodiment approach 3

[0037] Specific implementation mode three: this implementation mode is a further description of specific implementation mode one, and the specific process of step two is:

[0038] 2.1. Introducing a zero-mean white noise vector w into the discrete control system state equation k and v k , and satisfy: E{w k}=0, E{v k}=0, E{v k v j}=Rδ kj , where δ kj is the Kronecker symbol, E is the operation symbol for seeking expectation, and w k is the white noise of the system state vector at time k, v k is the white noise of the measurement vector at time k, w j is the white noise of the system state vector at time j, v j is the white noise of the measurement vector at time j, Q x is the white noise covariance matrix of the system state vector, and R is the white noise covariance matrix of the measurement vector;

[0039] 2.2. Through the actual operation to complete the w k and v k The calibration of these two white noises, according to the formula and E{v k v j}=Rδ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a method for estimating additive fault size of an executing agency of a satellite attitude control system through a second order Kalman filtering algorithm. The method for estimating the additive fault size of the executing agency of the satellite attitude control system through the second order Kalman filtering algorithm is achieved through the flowing steps of firstly, establishing a discrete control system model according to a kinetic equation and a kinematical equation; secondly, performing calibration on noise vectors wk and vk of the discrete control system model in an actual operational process; thirdly, establishing a discrete control system mathematical model which contains executing agency additive faults; fourthly, measuring a white noise vector in the output torque of the executing agency; and fifth, estimating the additive fault sizes of the executing agency through the second order Kalman filtering algorithm. The method for estimating the additive fault size of the executing agency of the satellite attitude control system through the second order Kalman filtering algorithm can be applied to a spacecraft attitude control field and aims at solving the problem that the size of a flywheel generated fault cannot be really reflected in modeling through a Kalman filtering algorithm in the existing satellite attitude control system.

Description

technical field [0001] This patent relates to the technical field of spacecraft attitude control systems, in particular to a method for estimating the magnitude of additive faults in actuators of satellite attitude control systems using second-order Kalman filter algorithms. Background technique [0002] The flywheel of the actuator in the satellite attitude control system is a component that rotates mechanically for a long time, and it is a component that is prone to failure in the satellite attitude control system. Moreover, after the flywheel has been in operation for a long time, a large friction torque will be generated in the flywheel. This friction torque can cause a constant deviation between the output torque of the flywheel and the expected output torque. This deviation can have an impact on the control accuracy of the satellite attitude control system. Transistor failure in the flywheel of the actuator or failure caused by missing command failure can also cause th...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B23/02G05B17/02
Inventor 陈雪芹李诚良王峰李冬柏耿云海
Owner 哈尔滨工大卫星技术有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com