Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

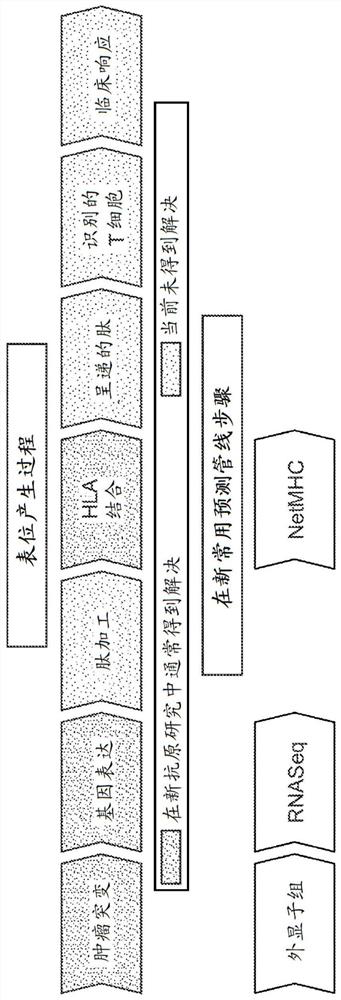
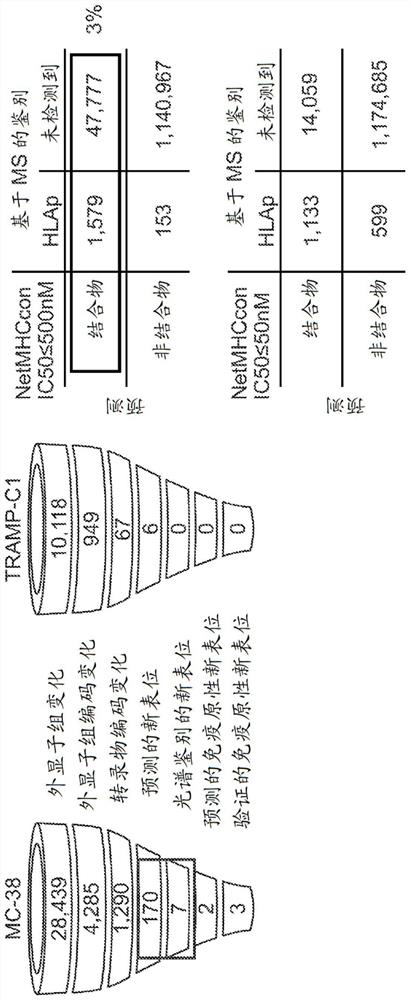
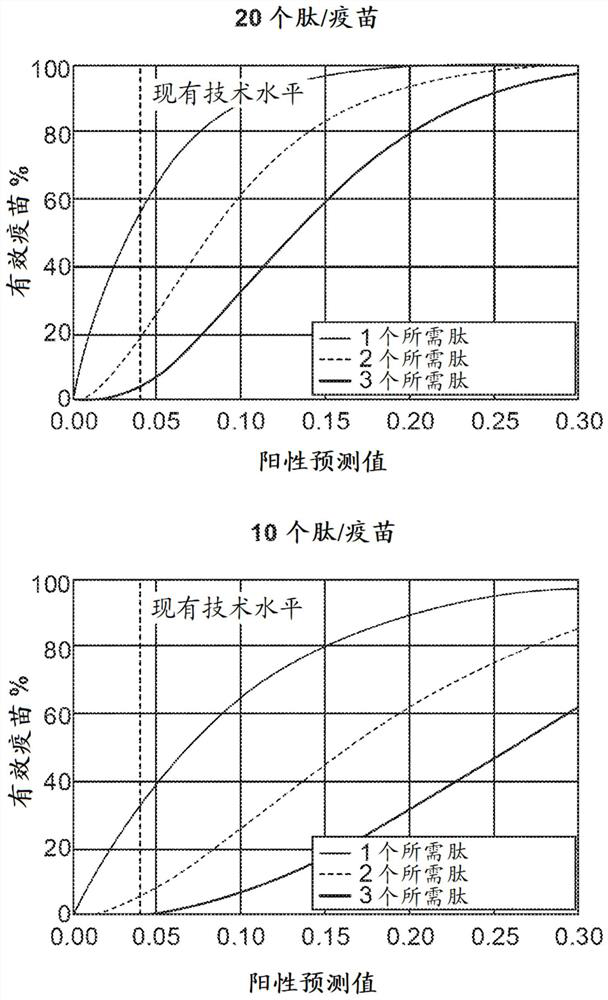
Neoantigen identification with pan-allele models

An allele and antigen technology, applied in genomics, receptors/cell surface antigens/cell surface determinants, library member identification, etc., can solve the problems of inefficient use of autoimmunity and missing candidate neoantigens in vaccines

Pending Publication Date: 2020-10-30
GRITSTONE BIO INC
View PDF39 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0009] Finally, standard approaches to tumor genome and transcriptome profiling may miss somatic mutations that generate candidate neoantigens due to suboptimal conditions for library construction, exome and transcriptome capture, sequencing, or data analysis
Likewise, standard tumor profiling methods may inadvertently contribute to sequence artifacts or germline polymorphisms as neoantigens, leading to inefficient use of vaccine potency or risk of autoimmunity, respectively

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Neoantigen identification with pan-allele models
  • Neoantigen identification with pan-allele models
  • Neoantigen identification with pan-allele models

Examples

Experimental program
Comparison scheme
Effect test

example

[0430] In another embodiment, the deviation parameter θ h 0 May be shared by gene families according to the MHC allele h. That is, the bias parameter θ of the MHC allele h h 0 can be equal to θ 基因(h) 0 , where gene (h) is the gene family of the MHC allele h. For example, the class I MHC alleles HLA-A*02:01, HLA-A*02:02, and HLA-A*02:03 can be assigned to the "HLA-A" gene family, and these MHC alleles The respective deviation parameter θ h 0 Can be shared. As another example, the class II MHC alleles HLA-DRB1:10:01, HLA-DRB1:11:01, and HLA-DRB3:01:01 can be assigned to the "HLA-DRB" gene family, and these MHC alleles The gene's respective bias parameter θ h 0 Can be shared.

[0431] Returning to equation (2), as an example, using the affine dependency function g h (·) Of the m = 4 different MHC alleles identified, the peptide p k The probability of being presented by the MHC allele h=3 can be given by:

[0432]

[0433] where x 3 k is the allelic interaction...

Embodiment 1

[0482] VIII.C.1. Example 1: Maximum of independent allele models

[0483] In one embodiment, the training module 316 makes the peptide p associated with a set of multiple MHC alleles H k The estimated probability of presentation u k Presentation probability u of each MHC allele h in pool H as determined based on cells expressing the monoallele k h∈H Variation modeling of , as described above in conjunction with equations (2)-(10). Precisely, the presentation probability u k can be u k h∈H of any function. In one embodiment, as shown in equations (11), (12a) and (12b), the function is a maximum function and presents the likelihood u k It can be determined as the maximum likelihood of presentation for each MHC allele h in set H.

[0484]

[0485] VIII.C.2. Example 2.1: Funciton-of-Sums model

[0486] In one embodiment, the training module 316 makes the peptide p by the formula k The estimated probability of presentation u k Modeling:

[0487]

[0488] where...

Embodiment 2

[0498] VIII.C.3. Example 2.2: Functional model using sums of allelic non-interacting variables

[0499] In one embodiment, the training module 316 incorporates allelic non-interacting variables and makes the peptide p by k The estimated probability of presentation u k Modeling:

[0500]

[0501] where w k represents the encoded related peptide p k Allelic non-interacting variables. Specifically, the set of parameters θ for each MHC allele h h and the set of parameters θ about the allele non-interacting variables w The value of θ can be obtained by making h and θ w is determined by minimizing the loss function of , where i is each instance in the subset S of training data 170 generated by cells expressing a single MHC allele and / or cells expressing multiple MHC alleles. Dependency function g w can take the form of the dependency function g described in section VIII.B.3 above w any of the forms.

[0502] Therefore, according to equation (14), the function g can b...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A method for identifying neoantigens that are likely to be presented by MHC alleles on a surface of tumor cells of a subject. Peptide sequences of the tumor neoantigens and of the MHC alleles are obtained by sequencing the tumor cells of the subject. The peptide sequences of the tumor neoantigens and of the MHC alleles are input into a machine-learned presentation model to generate presentation likelihoods for the tumor neoantigens, each presentation likelihood representing the likelihood that a neoantigen is presented by at least one of the MHC alleles on the surface of the tumor cells of thesubject. A subset of the neoantigens is selected based on the presentation likelihoods.

Description

[0001] CROSS-REFERENCE TO RELATED APPLICATIONS [0002] This application claims the benefit of and priority to US Provisional Application No. 62 / 636,061, filed on February 27, 2018. The contents of the applications cited above are incorporated by reference in their entirety. Background technique [0003] Therapeutic vaccines and T-cell therapies based on tumor-specific neoantigens hold great promise as the next generation of personalized cancer immunotherapy. 1–3 Given the relatively high probability of generating neoantigens, cancers with high mutational burdens, such as non-small cell lung cancer (NSCLC) and melanoma, are particularly interesting targets for this type of therapy. 4,5 Early evidence that neoantigen-based vaccination elicits T cell responses 6 And T-cell therapy targeting neoantigens can in some cases cause tumor regression in selected patients. 7 Both MHC class I and MHC class II have effects on T cell responses 70-71 . [0004] However, the identificati...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): C07K14/705C12Q1/70C40B20/06C40B30/10G01N27/49G01N33/48
CPCC40B30/04G01N33/6848G01N2333/70539G16B20/20G16B30/10G16B40/20G16B40/00C12Q1/6869G16B30/20
Inventor T·F·鲍彻B·布里克-沙利文J·巴斯比M·斯科伯恩R·耶冷斯凯
Owner GRITSTONE BIO INC
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com