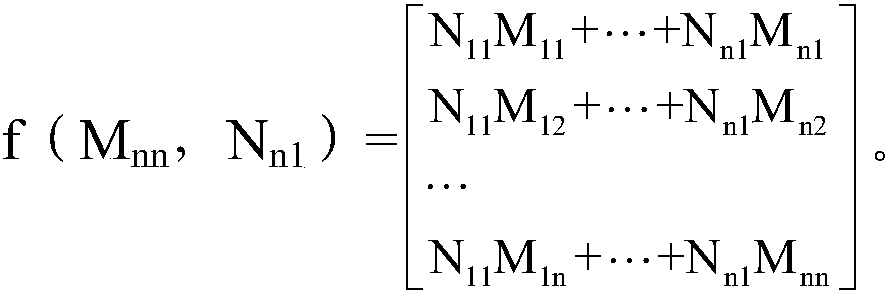Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Computing method applied to symmetric matrix and vector multiplication

A technology of symmetric matrix and vector multiplication, which is applied in the calculation field of symmetric matrix and vector multiplication, to achieve the effect of improving calculation efficiency and reducing waste

Active Publication Date: 2018-01-16
SUZHOU RICORE IC TECH LTD
View PDF5 Cites 15 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, there is no related work on the block calculation of symmetric matrices at this stage.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Computing method applied to symmetric matrix and vector multiplication
  • Computing method applied to symmetric matrix and vector multiplication
  • Computing method applied to symmetric matrix and vector multiplication

Examples

Experimental program
Comparison scheme
Effect test

no. 1 example

[0047] First embodiment, n1=64, m=8:

[0048] When n1=64, m=8, after block according to step S2, z=64 / 8=8, namely A ij is an 8×8 matrix, such as figure 1 As shown in FIG. 1 , eight 8×8 triangular matrix blocks (located on the diagonal) and 28 8×8 ordinary matrix blocks are obtained after block division. For eight 8×8 triangular matrix blocks A 11 、A 22 ...A 88 Perform microdata expansion to make it a symmetric matrix block ( figure 1 the shaded part in ). Block the 64-dimensional column vector with 8 as the side length, and block the data block B i1 A total of 8 rows (8 8×1 matrix B 11 , B 21 ...B 81 ), and then calculate the intermediate data block C z1 :

[0049] C i1 =A ii ×B i1 +...+A iz ×B z1

[0050] Among them, A ij with B i1 All are regarded as matrices, and the result of matrix multiplication is calculated by ordinary matrix multiplication, and the sum of 8 matrices is calculated according to the above formula, and C is obtained after calculation. ...

no. 2 example

[0060] Second embodiment, n1=7, m=2:

[0061] When n1=7, m=2, after block according to S2 step, z=[7 / 2]+1=4, namely A ij is a 2×2 matrix, such as figure 1 As shown, three 2×2 triangular matrix blocks (located on the diagonal), one 1×1 triangular matrix block, three 2×2 ordinary matrix blocks and three 2×1 matrix blocks are obtained after block division. For three 3×3 triangular matrix blocks A 11 、A 22 、A 33 Perform microdata expansion to make it a symmetric matrix block. Block the 7-dimensional column vector with 2 as the side length, and block the data block B i1 A total of 4 rows (3 2×1 matrix B 11 , B 21 , B 31 and a 1×1 matrix B 41 ), and then calculate the intermediate data block C z1 :

[0062] C i1 =A ii ×B i1 +...+A iz ×B z1

[0063] Among them, A ij with B i1 Both are regarded as matrices, and the result of matrix multiplication is calculated by ordinary matrix multiplication, and the sum of the four matrices is calculated according to the above fo...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a computing method applied to a symmetric matrix and vector multiplication. The method is used for computing the product of the (n1xn1) symmetric matrix and n1-dimensional column vectors, wherein first, the (n1xn1) symmetric matrix and the n1-dimensional column vectors are partitioned, and microscale data extension is performed on matrix blocks on diagonal lines of the (n1xn1) symmetric matrix after partitioning to turn the matrix blocks into symmetric matrix blocks; then the n1-dimensional column vectors are partitioned, an intermediate data block is computed accordingto the matrix after partitioning, and a final result vector is computed according to the intermediate data block. Through the computing method applied to the symmetric matrix and the vector multiplication, on the premise of performing parallel processing on the symmetric matrix, waste of storage space by the symmetric matrix can be reduced, and the computing efficiency of the symmetric matrix andthe vector multiplication can be improved.

Description

technical field [0001] The present invention relates to the fields of computer algorithm optimization and computer architecture. Specifically, the present invention relates to a method that can not only reduce the waste of storage space for symmetrical matrices, but also improve the The computational efficiency of multiplication with vectors is applied to the computational method of multiplication of symmetric matrices with vectors. Background technique [0002] Matrix and vector multiplication are widely used in the field of high-performance numerical computing (such as process control, image processing, numerical analysis, scientific computing, solving dynamic programming problems, signal processing, theoretical physics, solid state physics, coding theory, cryptography, linear prediction and computer timing analysis. etc.) has a very important role and is a typical application with intensive computing and memory access characteristics. According to statistics, in high-per...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/16
Inventor 薛瑞张浩范东睿叶笑春朱亚涛
Owner SUZHOU RICORE IC TECH LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com