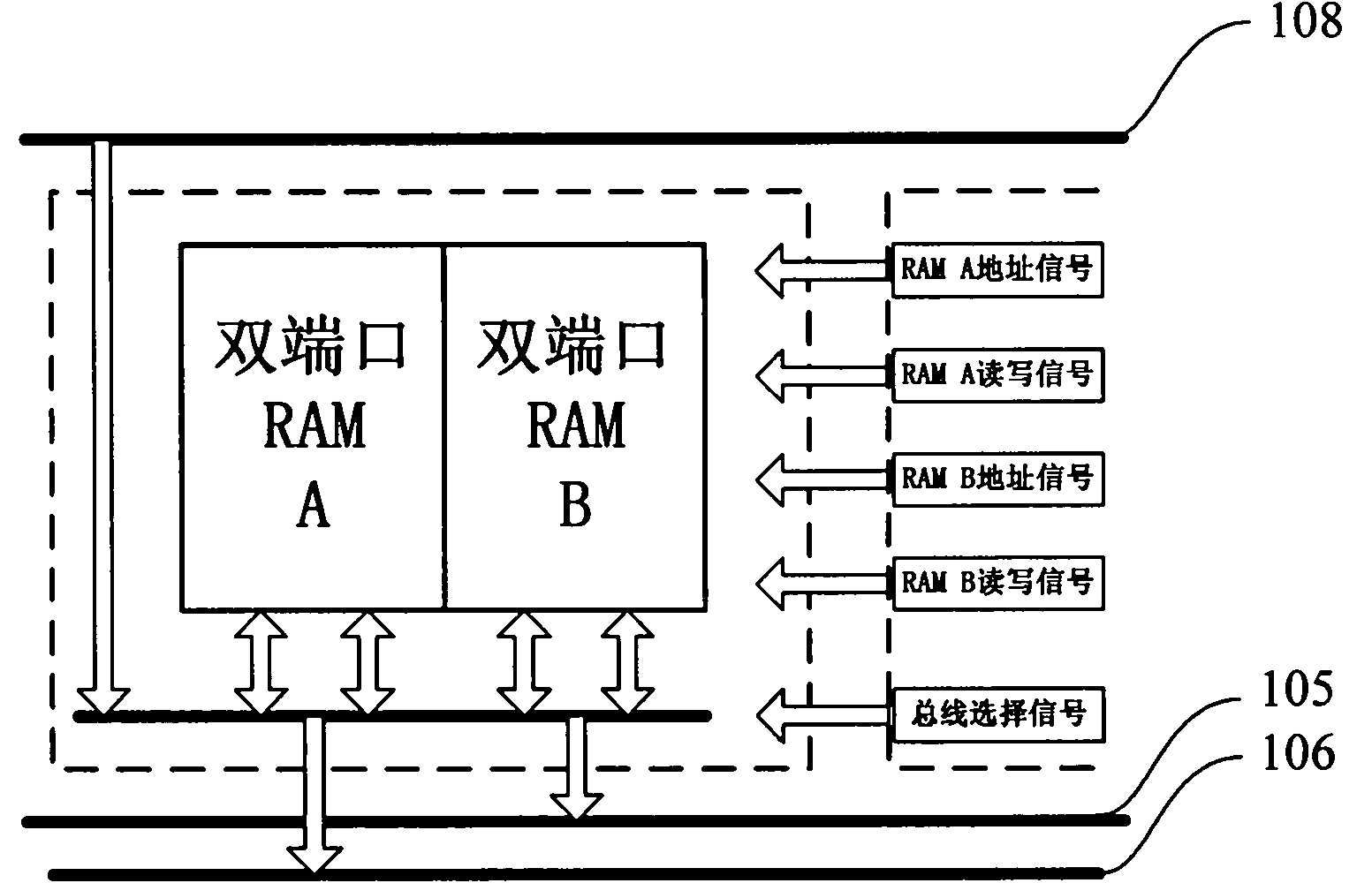
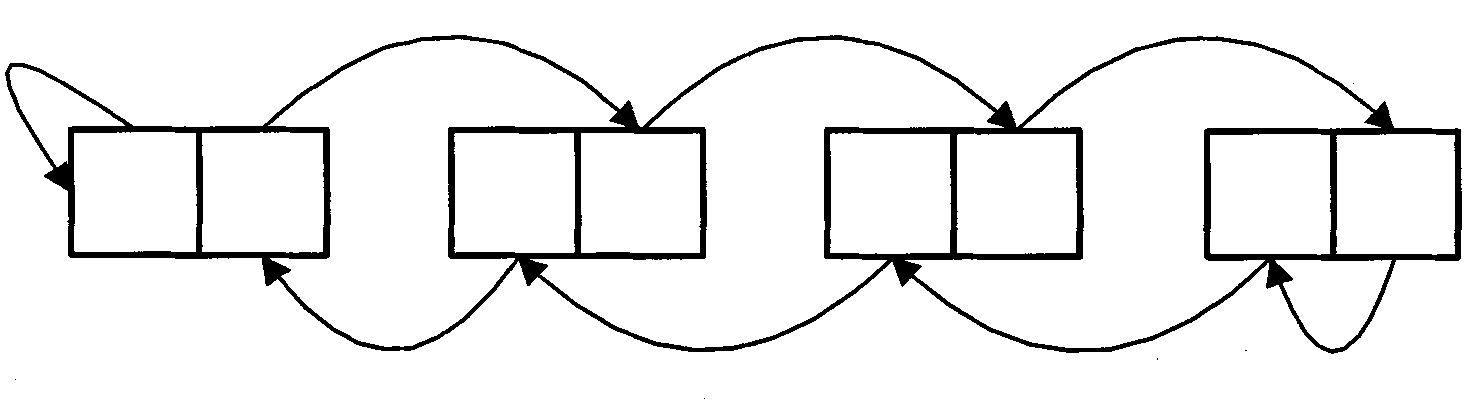
Device for decomposing characteristics of real symmetric matrix based on circular Jacobian
An eigendecomposition and symmetric technology, which is applied in the calculation using the number system, computing using non-contact manufacturing equipment, instruments, etc. It can solve the problem of difficult large-scale matrix eigendecomposition, consuming large hardware resources, and low computing performance. problem, to achieve the effect of optimizing the traversal order, high data throughput, and improving overall performance
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0036] In order to make the above objects, features and advantages of the present invention more comprehensible, the present invention will be further described in detail below in conjunction with the accompanying drawings and specific embodiments.
[0037] Before introducing the specific implementation of the present invention, the cyclic Jacobian algorithm will be described first. For a real symmetric matrix A, if there is an orthogonal matrix Q, it can be similarly transformed into a diagonal matrix Σ, as shown in the following formula:
[0038] Q T AQ=∑;
[0039] where the superscript T represents the transpose of a vector or matrix. Then the elements on the ∑ diagonal are the eigenvalues of A, and the columns in Q are the corresponding eigenvectors. Note the rotation matrix as W(p, q, θ), where p>q, and the elements in the rotation matrix are defined as follows: w pp =cosθ,w pq = sinθ, w qp =-sinθ,w qq =cosθ, while the rest of the diagonal elements are all 1, and...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D Engineer
- R&D Manager
- IP Professional
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com