Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

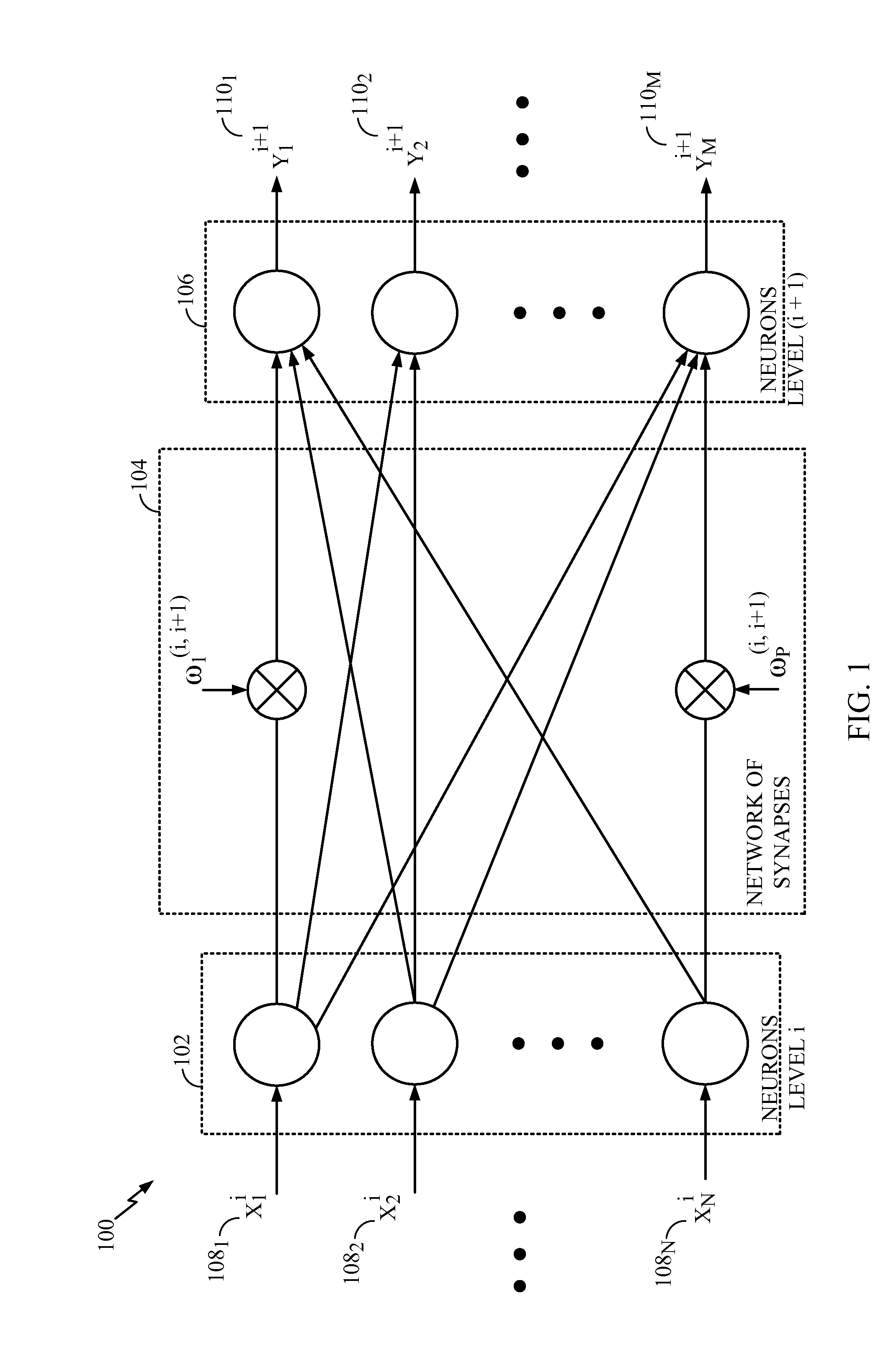
Piecewise linear neuron modeling

a neuron modeling and piecewise technology, applied in the field of artificial nervous systems, can solve problems such as inability to find exact solutions, and achieve the effect of accurate modeling of dynamics and low complexity

Inactive Publication Date: 2014-05-22
QUALCOMM INC
View PDF0 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

The present disclosure provides methods and apparatus for approximating nonlinear functions of neuron models as piecewise linear functions. This results in a simpler and more accurate model for neurons that can be easily implemented in artificial neurons. The design goal is to create a flexible architecture that can accommodate different neuron models with simple parameter changes. The use of piecewise linear approximations allows for easy swapping of different neuron models and ensures accurate modeling of neuron dynamics.

Problems solved by technology

Since the system is nonlinear, exact solutions cannot be found.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Piecewise linear neuron modeling
  • Piecewise linear neuron modeling
  • Piecewise linear neuron modeling

Examples

Experimental program
Comparison scheme
Effect test

example 1

Taylor Expansion for the Izhikevich (Simple) Model

[0164]In this example, Eq. (68) is evaluated for the simple model and linearization based on the Taylor expansion method. To simplify the formulas somewhat, it is assumed that the external current is not present.

[0165]First, the coefficients of the Taylor expansion for the simple model, i.e., F(v)=k(v−vr)(v−vt), are derived starting from Eq. (56). Provided that

1C∂F(v)∂v|vn=2kCvn-kC(vr+vt)(69)

one obtains

a11[vn,nT]=2kCvn-kC(vr+vt)+1C∑i=1Lgi(nT)[hi′(vn)(Ei-vn)-hi(vn)](70)b1[vn,t]=Γ(vn,t)-a11[vn,nT]vn=1C{k(vn-vr)(vn-vt)+∑i=1Lgi(t)hi(vn)(Ei-vn)}-{2kCvn2-kC(vr+vt)vn+1C∑i=1Lgi(nT)[hi′(vn)(Ei-vn)-hi(vn)]vn}(71)

[0166]For non-NMDA synaptic channels, Eqs. (70) and (71) simplify to

a11[vn,nT]=2kCvn-kC(vr+vt)-1C∑i=1Lgi(nT)(72)b1[vn,nT]=1C{-kvn2+kvrvt+∑i=1Lgi(nT)vn}+1C∑i=1Lgi(t)(Ei-vn)(73)

[0167]Taking

b0=1C{-kvn2+kvrvt+∑i=1Lgi(nT)[hi′(vn)(Ei-vn)-hi(vn)]vn}

Eq. (68) now becomes

x(nT+T)=AnTx(nT)+An-1(AnT-I)[b0b2]+∑i=1L[hi(vn)(Ei-vn)]∫0TAnτgi(nT+T-τ)τ[10...

example 2

Subthreshold Dynamics of the Hunzinger Cold Model

[0171]Another example is developed in an effort to examine the subthreshold dynamics of the simple intrinsic conductance model known as the Hunzinger Cold model. In this example, no synaptic currents and the simple, but interesting case of impulsive external current are assumed.

[0172]In the Hunzinger Cold model (see Eq. (22) above) when the membrane voltage is below threshold, the matrix, An is constant and equal to A−:

A-≡[-1 / τ--1 / Cab-a]

[0173]The derivation can be further simplified if the first state variable is defined as the membrane voltage minus the reference voltage. With such a definition, all the constant terms are equal to zero, and Eq. (61) simplifies to

x(t)=A-(t-Tn)x(Tn)+1C∫TntA-(t-τ)Iext(τ)τ[10](77)

[0174]Furthermore, if the external current is assumed to be a Dirac delta function at time Tn with amplitude I, i.e., Iext=(t)+Iδ(t−Tn), then

x(t)=A-(t-Tn)(x(Tn)+1C[10])(78)

[0175]Note that impulsive inputs have the same effect on...

example 3

Approximation with a Backward Rectangular Rule

[0189]To simplify the exposition and notations, this example assumes that the synaptic current does not contain voltage-dependent conductance channels (e.g., NMDA channels) and that there is no external current Iext(t). The derivation is obtained for fixed step sizes of length T. To begin, Eq. (68) may be simplified as follows:

x(nT+T)=AnTx(nT)+q+1C∫0TAnτ∑i=1Lgi(nT+T-τ)(Ei-v(nT+T))τ[10](98)

where the vector q contains constant terms, namely

q=An-1(AnT-I)[b0b2](99)

[0190]For notational convenience, the following vector and matrix may also be defined:

b≡[10]B≡[1000](100)

such that Eq. (98) may be rewritten as

x(nT+T)=AnTx(nT)+1C∫0TAnT∑i=1Lgi(nT+T-τ)Eiτb-1C∫0TAnτ∑i=1Lgi(nT+T-τ)τB·x(nT+T)+q(101)

[0191]Now, the solution is derived for gi(t) modeled as simple exponentials per Eq. (29). In this case, one has

x(nT+T)=AnTx(nT)+1C∑i=1Lgi(nT)Ei∫0TAnτ-(T-τ) / τiτ·b-1C∑i=1Lgi(nT)∫0TAnτ-(T-τ) / τiτB·x(nT+T)+q(102)

[0192]The integrals can be readily solved, and if o...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

Methods and apparatus for piecewise linear neuron modeling and implementing one or more artificial neurons in an artificial nervous system based on one or more linearized neuron models. One example method (for implementing a combination of a plurality of neuron models in a system of neural processing units) generally includes loading parameters for a first neuron model selected from the plurality of neuron models into a first neural processing unit, determining a first state of the first neural processing unit based at least in part on the parameters for the first neuron model, and determining a second state of the first neural processing unit based at least in part on the parameters for the first neuron model and on the first state. This method may also include updating the plurality of neuron models (e.g., by adding, deleting, or adjusting parameters for the first neuron model or another neuron model).

Description

CLAIM OF PRIORITY UNDER 35 U.S.C. §119[0001]This application claims benefit of U.S. Provisional Patent Application Ser. No. 61 / 728,360, filed Nov. 20, 2012 and entitled “Piecewise Linear Neuron Modeling,” U.S. Provisional Patent Application Ser. No. 61 / 734,716, filed Dec. 7, 2012 and entitled “Piecewise Linear Neuron Modeling,” U.S. Provisional Patent Application Ser. No. 61 / 740,633, filed Dec. 21, 2012 and entitled “Piecewise Linear Neuron Modeling,” and U.S. Provisional Patent Application Ser. No. 61 / 756,889, filed Jan. 25, 2013 and entitled “Piecewise Linear Neuron Modeling,” all of which are herein incorporated by reference in their entireties.BACKGROUND[0002]1. Field[0003]Certain aspects of the present disclosure generally relate to artificial nervous systems and, more particularly, to approximating at least a portion of a nonlinear function of a neuron model as a piecewise linear function and to using the resulting linearized neuron model in one or more artificial neurons.[000...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(United States)
IPC IPC(8): G06N3/02
CPCG06N3/049G06N3/04G06N3/063G06N3/08G06N3/082G06N20/00
Inventor PADOVANI, ROBERTOYOON, YOUNG CHEUL
Owner QUALCOMM INC
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com