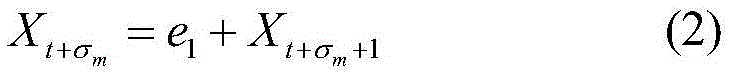Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Optimizing method of split-radix FFT (fast fourier transform) algorithm based on ternary tree

An optimization method and ternary tree technology, applied in the optimization field of split-radix FFT algorithm

Inactive Publication Date: 2016-06-01
合肥康捷信息科技有限公司
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The present invention is in order to overcome the deficiencies existing in the prior art, and provides a kind of optimization method of split-based FFT algorithm based on ternary tree, in order to solve the problem of reducing the system overhead in the calculation process of split-based algorithm, so as to improve the Fourier transform Performance during calculation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimizing method of split-radix FFT (fast fourier transform) algorithm based on ternary tree
  • Optimizing method of split-radix FFT (fast fourier transform) algorithm based on ternary tree
  • Optimizing method of split-radix FFT (fast fourier transform) algorithm based on ternary tree

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0072] In the present embodiment, a kind of optimization method based on the split-base FFT algorithm of ternary tree is to carry out as follows:

[0073] Step 1. Global definition

[0074] Define the source vector of the split-basis FFT algorithm as X[X 0 ,X 1 ,...,X k ,...,X N-1 ]; N represents the length of the source vector; X k Represents the k+1th complex data in the FFT algorithm;

[0075] Define the twiddle factor array as W[W 0 ,W 1 ,...,W k ,...,W N-1 ]; W k Indicates the k+1th twiddle factor; 0≤k≤N-1;

[0076] In the implementation process, each element in the FFT source vector and the twiddle factor array is a complex number data, and a complex number can generally be represented by a real part and an imaginary part. For example, y=r+uj means that a real part is r, The imaginary part is the complex number of u.

[0077] Define global variables as β, γ;

[0078] Define the linked list L;

[0079] The calculation information defining each node in the te...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an optimizing method of a split-radix FFT (fast fourier transform) algorithm based on a ternary tree. The optimizing method comprises the following steps of 1, defining the ternary tree and information of tree nodes; 2, according to the particular FFT computing scale, enabling the ternary tree to generate computing information; 3, browsing the ternary tree by a width priority searching algorithm, obtaining the information in the computing process, and storing the computing information into a chain list; 4, utilizing the computing information of the nodes in the chain list to optimize the split-radix FFT algorithm. The optimizing method has the advantages that the problem of low efficiency in the traditional recursion is solved, the system expense is reduced when the recursion calls up the subfunction, the division of computing tasks in the split-radix algorithm is completed in advance, and the efficiency is improved.

Description

technical field [0001] The invention belongs to the technical field of electric digital data processing, in particular to an optimization method of a split-based FFT algorithm based on a ternary tree. Background technique [0002] The split-based FFT algorithm is an algorithm for fast calculation of the discrete Fourier transform, invented by P.Duhamel and H.Hollmann, which can calculate one-dimensional real and complex data and the discrete Fourier of an integer power of 2 leaf transformation. Different from the base-2 FFT algorithm, the split-base FFT algorithm converts the calculation of the large-scale Fourier transform into the calculation of three small-scale sub-Fourier transforms, thereby recursively dividing the sub-Fourier transforms, and finally completes The calculation process of FFT. Compared with the radix-2 algorithm, it has less calculation and can be well used in signal processing and other fields. [0003] However, the main implementation of the split-b...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/14
CPCG06F17/14
Inventor 顾乃杰张明任开新
Owner 合肥康捷信息科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com