Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Airborne MIMO radar robust dimension-reduction space-time self-adaptive processing method

A processing method and dimensionality reduction technology, which are applied in the field of robust dimensionality reduction space-time adaptive processing and the robust dimensionality reduction space-time adaptive processing of airborne MIMO radar, which can solve the problem of difficult to meet real-time processing requirements and increase the number of training samples Demand, performance degradation, etc.

Inactive Publication Date: 2016-07-20
THE PLA INFORMATION ENG UNIV
View PDF5 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Due to the diversity of transmitted waveforms, the airborne MIMO radar STAP further increases the number of training samples while obtaining the expansion of system degrees of freedom. However, it is difficult to obtain enough independent and identically distributed (IID) sample data for covariance matrix estimation in practice. Moreover, the computational complexity has been significantly increased, and the computational complexity of the algorithm is particularly prominent, which makes it difficult to meet the real-time processing requirements. These are also key issues that need to be solved urgently in the process of promoting MIMO-STAP technology to realize practical engineering applications.
At the same time, the existing dimensionality reduction STAP methods (such as the double iterative algorithm) that reduce the number of samples and computational complexity only consider the ideal situation where the array steering vector is precisely known. However, in practical engineering applications, various error situations are inevitable, such as When there is an error in the direction of arrival (DOA) and velocity of the target in STAP, it will cause a mismatch between the airspace and time domain steering vectors of the desired target, and there will be error coupling between them, which will cause the performance of the traditional dimensionality reduction STAP method when it is applied to airborne MIMO radar. drop, or even fail

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Airborne MIMO radar robust dimension-reduction space-time self-adaptive processing method
  • Airborne MIMO radar robust dimension-reduction space-time self-adaptive processing method
  • Airborne MIMO radar robust dimension-reduction space-time self-adaptive processing method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

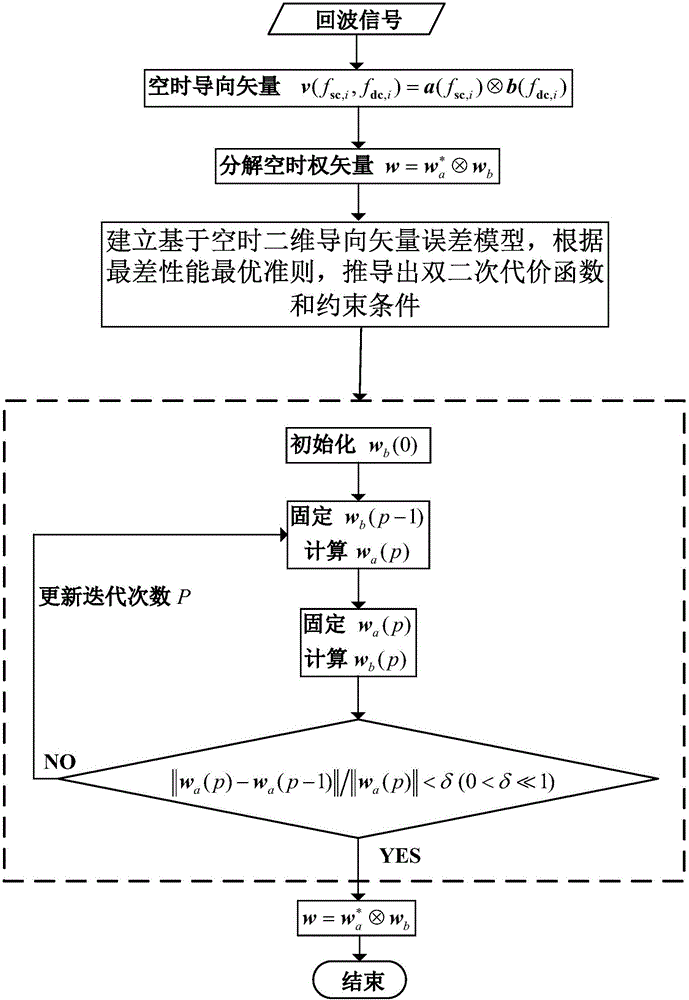
[0046] Embodiment one, see Figure 1~2 As shown, a robust space-time adaptive processing method for airborne MIMO radar includes the following steps:

[0047] Step 1. Separate the MNK × 1-dimensional space-time two-dimensional steering vector w in the airborne MIMO radar into MN × 1-dimensional airspace steering vector w a and K×1-dimensional time-domain steering vector w b , Among them, M is the number of transmitting array elements, N is the number of receiving array elements, K is the number of coherent pulses, and the symbol Indicates the Kronecker product, and the superscript * indicates the conjugation of a vector or matrix;

[0048] Step 2. Establish a space-time two-dimensional steering vector error model, and deduce the biquadratic cost function according to the optimal criterion of the worst performance as The constraints are in, is the matrix form of the received data vector, a and b represent the assumed space-domain steering vector and time-domain steer...

Embodiment 2

[0051] Embodiment two, see Figure 1~5 As shown, a robust space-time adaptive processing method for airborne MIMO radar includes the following steps:

[0052] Step 1. Separate the MNK × 1-dimensional space-time two-dimensional steering vector w in the airborne MIMO radar into MN × 1-dimensional airspace steering vector w a and K×1-dimensional time-domain steering vector w b , Among them, M is the number of transmitting array elements, N is the number of receiving array elements, K is the number of coherent pulses, and the symbol Indicates the Kronecker product, and the superscript * indicates the conjugation of a vector or matrix;

[0053] Step 2. Establish a space-time two-dimensional steering vector error model, and deduce the biquadratic cost function according to the optimal criterion of the worst performance as The constraints are in, is the matrix form of the received data vector, a and b represent the assumed space-domain steering vector and time-domain steer...

Embodiment 3

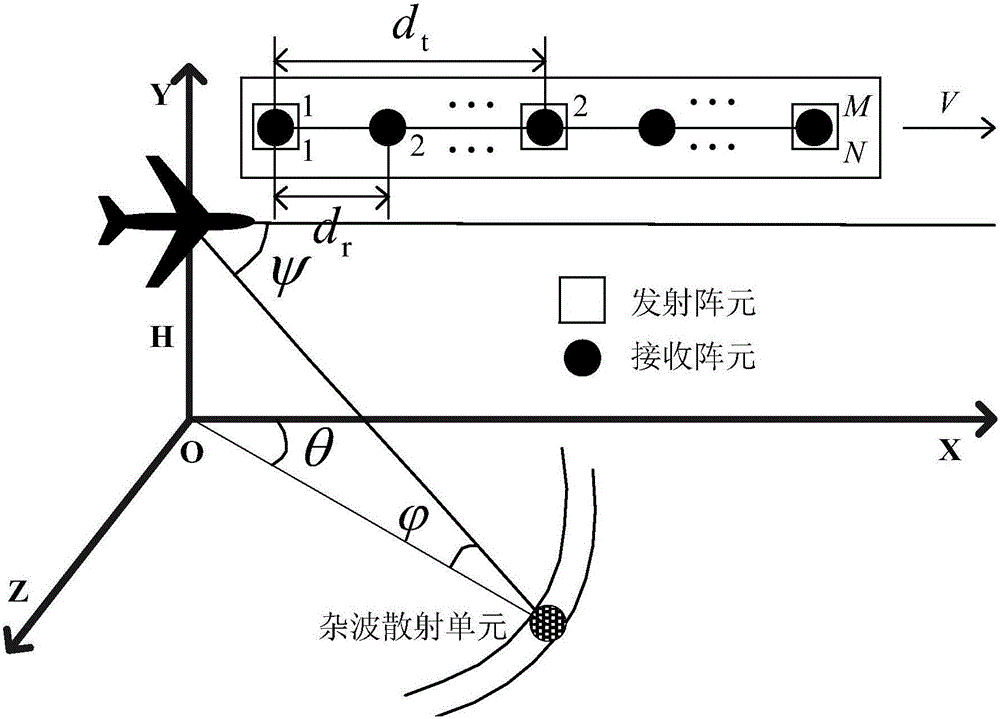
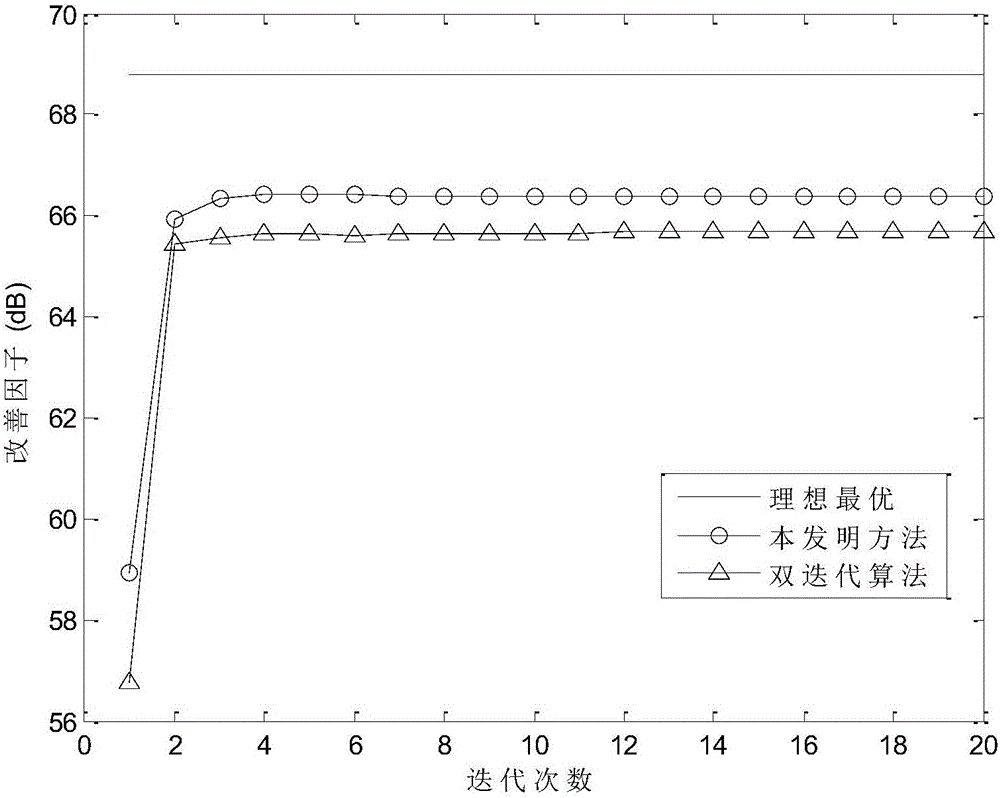
[0082] Embodiment three, see Figure 1~5 Shown, in conjunction with specific embodiment the present invention is described in further detail, figure 1 In , it is assumed that the height of the radar carrier is H, and it is flying in a straight line at a constant speed V along the positive direction of the X axis. The direction of the MIMO radar antenna array is perpendicular to the flight direction of the carrier aircraft, and the operating wavelength of the radar is λ. It has M transmitting array elements and N receiving array elements, all of which are omnidirectional antennas, and are evenly arranged on the front side, with a spacing of d t and d r =λ / 2. Assuming a uniform distribution N in the distance gate c clutter scattering unit, the i-th (i=1,2,...,N c ) The azimuth angle of the clutter unit is θ i , and the pitch angle from the gate is The cone angle is ψ. Then the corresponding airspace transmitting and receiving steering vectors are and in is the norm...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an airborne MIMO radar robust dimension-reduction space-time self-adaptive processing method, which comprises the following steps: to begin with, decomposing MIMO-STAP weight vector into Kronecker product of space and time two low-dimension weight vectors; then, based on an error model of space and time steering vectors, carrying out deduction through a second-order convex optimization algorithm to obtain a bi-quadric cost function and constraint conditions; carrying out cycle optimization solution on the space and time two low-dimension weight vectors through a double iterative algorithm; and finally, enabling the space and time weight vectors obtained through optimization to be synthesized into a full-dimensional MIMO-STAP weight vector. In the dimension-reduction processing, robust processing is carried out on each dimension of solution, so that dimension is reduced, and meanwhile, robustness of the steering vector error is enhanced; and under the condition of same sample number and algorithm complexity, the method has higher robustness.

Description

technical field [0001] The present invention relates to the technical field of radar signal processing, in particular to a robust dimensionality reduction space-time adaptive processing method for airborne MIMO radars, which realizes robust dimensionality reduction spacetime in the case of mismatched expected target vectors of airborne MIMO radars. Time adaptive processing for clutter suppression and moving target detection. Background technique [0002] As a new radar system, multiple-input multiple-output (MIMO) radar has opened up a broader technical idea for improving the performance of traditional radar, and has become a research hotspot in the international radar field. According to the array element configuration and signal processing method, the current research mainly divides MIMO radar into two types, namely: distributed MIMO radar and centralized MIMO radar. The distributed MIMO radar has a large antenna spacing, which enables the radar to observe targets from di...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S7/36
CPCG01S7/36
Inventor 王珽赵拥军陈世文赵闯张昆帆王建涛赵远
Owner THE PLA INFORMATION ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com