Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Fast encoding and decoding method and system for erasure coded data

A decoding method and fast coding technology, which are applied in the fast coding and decoding method and system field of erasure code data, can solve the problems of unfavorable promotion, slow operation speed, and increased system cost, and achieve the effect of reducing the number of operations and improving the processing speed

Active Publication Date: 2019-03-19
SUNING COM CO LTD
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Based on the above analysis, in the prior art, the coding complexity of Vandermonde code is O(mn), and the decoding complexity is O(n 3 ); the encoding complexity of the Cauchy code is O(mn), and the decoding complexity is O(n 2 )
If the RS codec is implemented by software, the operation speed is very slow, generally only 50-100MB / s in the existing technology, which greatly limits the use of RS erasure codes
For this reason, many applications and cloud storage systems have to use dedicated FPGA (Field Programmable Gate Array) hardware to accelerate RS operations, but this increases the system cost and is also not conducive to its promotion.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fast encoding and decoding method and system for erasure coded data
  • Fast encoding and decoding method and system for erasure coded data
  • Fast encoding and decoding method and system for erasure coded data

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

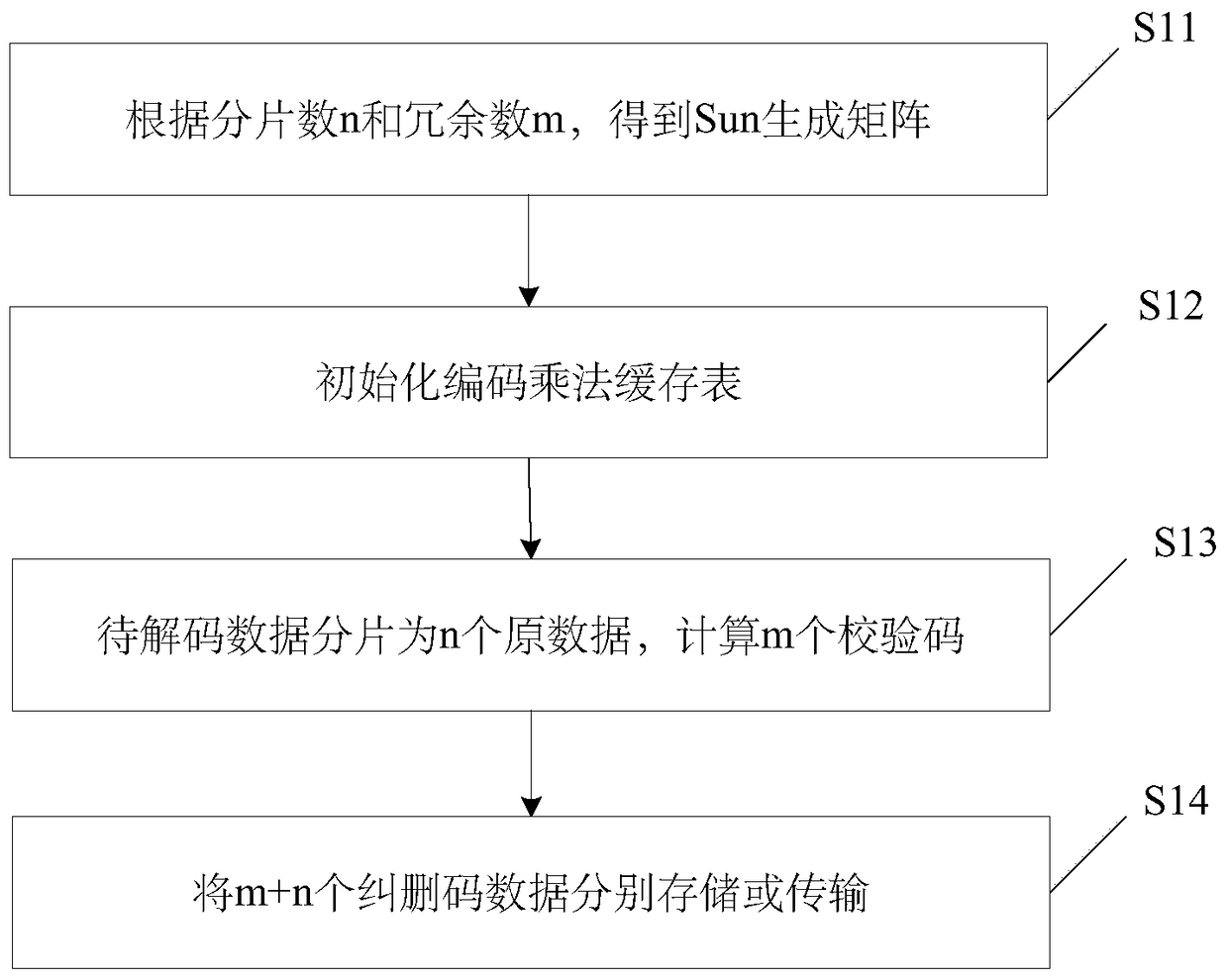
[0074] In a preferred embodiment of the present invention, in step S11 of the coding method (or step S21 of the coding method), the generating matrix is ​​an m×n matrix. Since any number multiplied by 1 is itself, using as many 1s as possible in the generator matrix can reduce the number of multiplications. When transforming the Vandermonde matrix to obtain the generating matrix, it is only necessary to set the first row element to be 1. For example, for the Vandermonde matrix G1 in the above background technology, let a 1 =1 to get the first generating matrix (or call it the Vandermond-Sun matrix):

[0075] Each of them a i are different from each other and not 0, a typical example is

[0076]

[0077] When transforming the Cauchy matrix to obtain the generating matrix, the Cauchy matrix needs to be transformed twice in rows and columns, so that the first row and the first column are both 1: the first row and column transformation, multiply all rows by the row No. The...

Embodiment 2

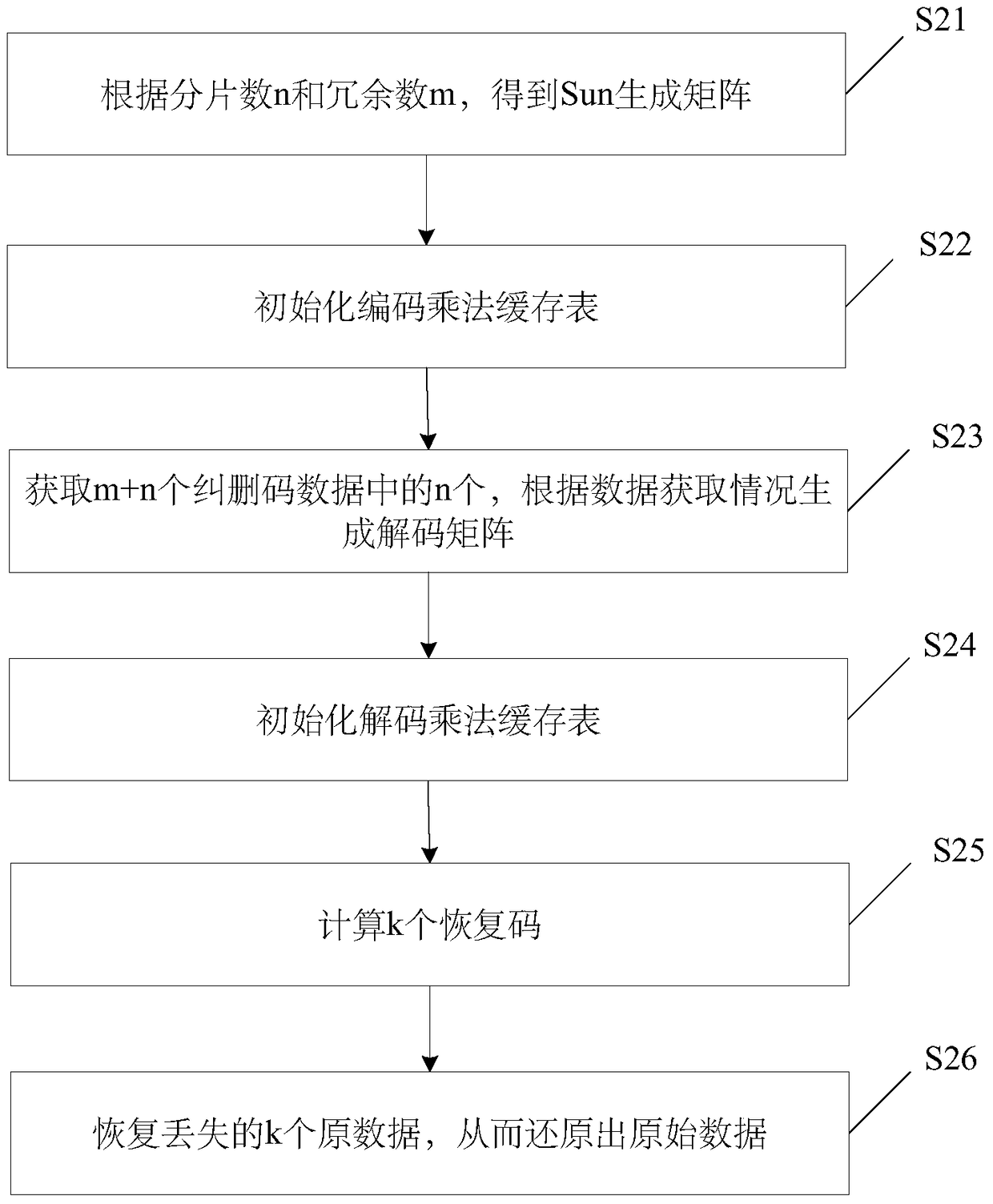
[0112] When decoding, if the original data fragments that do not exceed the redundancy number m of the check code are lost, the check code block can be used to participate in decoding to obtain the lost original data blocks. The traditional Reed-Solomon decoding method needs to solve the inverse matrix of the n×n order square matrix, which requires O(n 3 ) calculation amount (using Gaussian elimination method, where n is the number of original data slices).

[0113] The decoding method of the present invention does not need to calculate the inverse matrix of the n×n order square matrix, but only needs to calculate the k×k order square matrix decoding matrix G little The inverse matrix of , where k is the number of check code blocks used in decoding, has 0<k≤m (when k is 0, it means that the original data blocks have been received, and the decoded data can be directly composed without using the decoding matrix) . Since k is always less than or equal to the number n of origina...

Embodiment 3

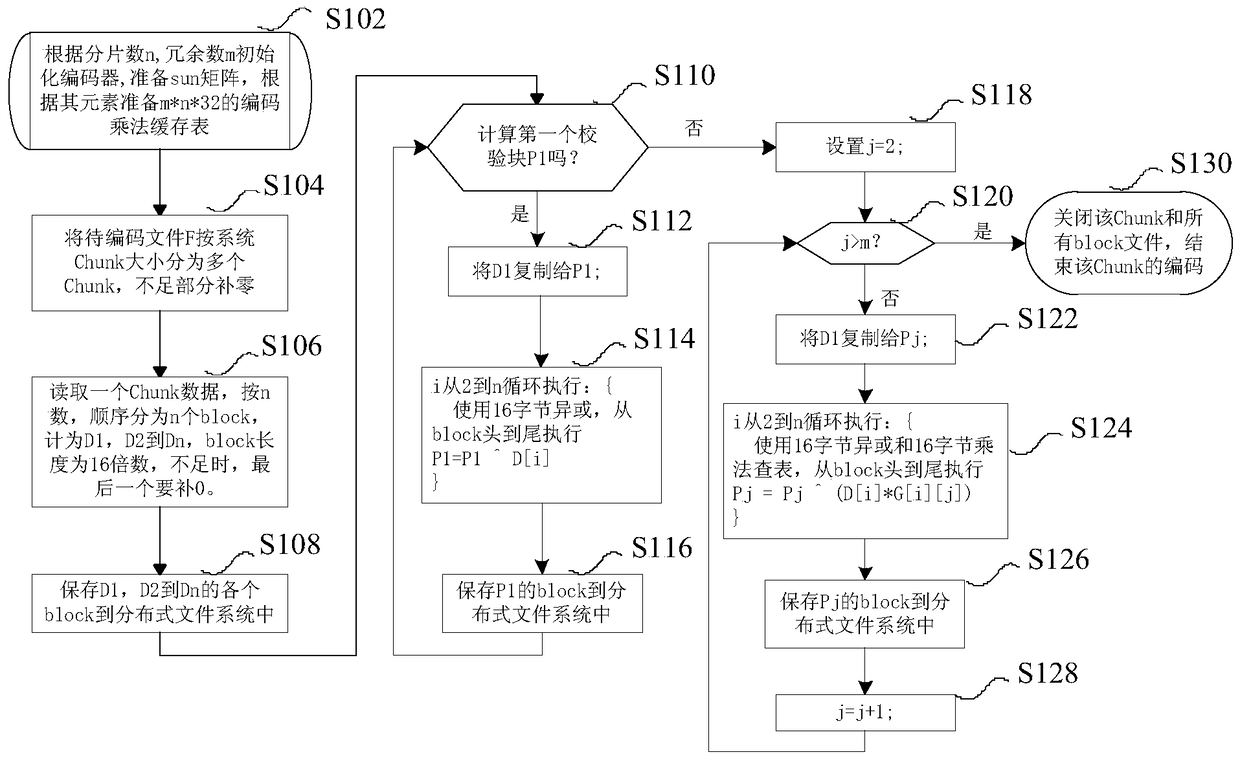
[0133] See attached image 3 In another preferred embodiment of the present invention, the process of the encoding method is further described in the form of a computer detailed data processing flow:

[0134] Step S102 : Initialize the encoder according to the slice number n and the redundancy number m, and prepare to generate the matrix. Here, the Sun matrix is ​​selected as the generating matrix, and its characteristic is that the first row and the first column of the matrix are both 1. The generator matrix can be transformed from a Vandermonde matrix or a Cauchy matrix. Such as the example transformed by the Cauchy matrix, using G ij =A matrix in the form of (i×j) / (i+j-1), where i and j represent the rows and columns of the matrix, respectively.

[0135] Then, according to the m×n elements of the Sun matrix, prepare an m×n×32-byte encoded multiplication cache table to store each element G in the Sun matrix ij Galois field multiplicative data for . For each element, u...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to the technical field of data coding and decoding, and discloses a quick coding and decoding method and system of erasure code data. The coding method of the erasure code data comprises the following steps: according to a fragmentation number n and a redundant number m, through the conversion of a Vandermonde matrix or a Cauchy matrix, obtaining a generation matrix of which the first line element and the first row element are independently 1; initializing a coding multiplication cache table; dividing data to be coded into n pieces of original data, and utilizing the multiplication cache table to calculate m check codes according to the n pieces of original data and the generation matrix; and independently storing and / or transmitting the n pieces of original data and the obtained m check codes. The generation matrix used by the coding method ensures that a Galois field multiplication operation amount can be reduced during both coding and decoding, is compatible with a copy algorithm, and drastically improves the processing speed of the erasure code data, and therefore, the reliability and the effectiveness of data in a distributed system, especially a cloud storage system, are guaranteed under a situation that data processing efficiency is not lowered and hardware cost is not increased.

Description

technical field [0001] The invention relates to the technical field of data encoding and decoding, in particular to a fast encoding and decoding method and system for erasure correction coded data. Background technique [0002] When computer data is transmitted or stored, some information is often lost due to problems such as noise or equipment damage. In order to maintain the reliability and validity of data, the purpose of error tolerance and error correction can be achieved by adding redundant check codes when encoding information. This type of technology is usually called Erasure Codes (EC for short, also known as known as erasure codes, error correction codes, etc.) technology. There are generally two types of EC used in cloud storage, namely, Reed-Solomon erasure code (referred to as RS erasure code) and low density parity check code (Low Density Parity Check Code, referred to as LDPC erasure code). Among them, the RS erasure code has the MDS (Maximum Distance Separa...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F11/10H03M13/15
Inventor 孙崎
Owner SUNING COM CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com