Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Distributed adaptive neural network continuous tracking control method for multi-robot systems

A neural network and multi-robot technology, applied in the direction of adaptive control, general control system, control/regulation system, etc., can solve problems such as external interference and multi-robot system parameter uncertainty

Active Publication Date: 2017-06-23
成都川哈工机器人及智能装备产业技术研究院有限公司
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0049] The purpose of the present invention is to solve the problem that the existing multi-robot system coordination tracking control method makes the multi-robot system have parameter uncertainty and external interference, and proposes a multi-robot system distributed adaptive neural network continuous tracking control method

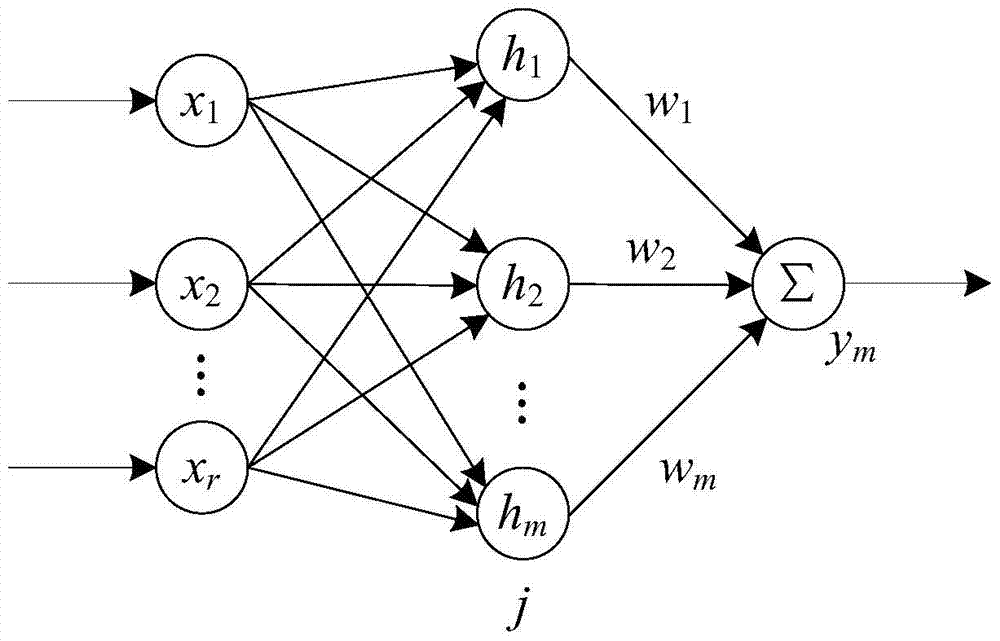
Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Distributed adaptive neural network continuous tracking control method for multi-robot systems
  • Distributed adaptive neural network continuous tracking control method for multi-robot systems
  • Distributed adaptive neural network continuous tracking control method for multi-robot systems

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0087] combine figure 1 with Figure 5 Describe the multi-robot system distributed adaptive neural network continuous tracking control method in this embodiment. First, introduce the related technologies applied in this embodiment:

[0088] 1. Euler-Lagrange model:

[0089] According to the Euler-Lagrange model:

[0090]

[0091] Indicates the motion equation of the i-th following robot; where q i ∈ R p Denotes follower generalized coordinates, M i (q i )∈R p×p represents the symmetric positive definite inertia matrix, Denotes the Coriolis force and centripetal force matrix, G i (q i )∈R p represents the gravity constraint matrix, τ i ∈ R p Denotes the generalized control force acting on follower i, ω i ∈ R p Indicates external interference. Among them, M i (q i ), G i (q i ) are unknown quantities.

[0092] 2. Distributed tracking control:

[0093] Tracking control refers to the coordinated control problem in which there is only one leader in a mult...

specific Embodiment approach 2

[0167] Different from the specific embodiment 1, the Euler-Lagrange model described in step 1 satisfies antisymmetry and boundedness in the multi-robot system distributed adaptive neural network continuous tracking control method of this embodiment: is an antisymmetric matrix, given any vector x i ∈ R p Have The boundedness refers to the existence of normal constants and k m , making where I p is a p×p order identity matrix.

[0168] Prove that the observer is bounded

[0169] Since the navigator is dynamic, according to the navigator's time-varying velocity formula and time-varying trajectory formula, v is a time variable, so v(t-τ)≠v(t). Therefore, substituting the time-varying velocity formula (6) and the time-varying trajectory formula (7) into the control formula (8) of the distributed observer can get:

[0170] in:

[0171]

[0172] Choose the Lyapunov function:

[0173]

[0174] Define neutral operator And know the neutral operator is stable,...

Embodiment 1

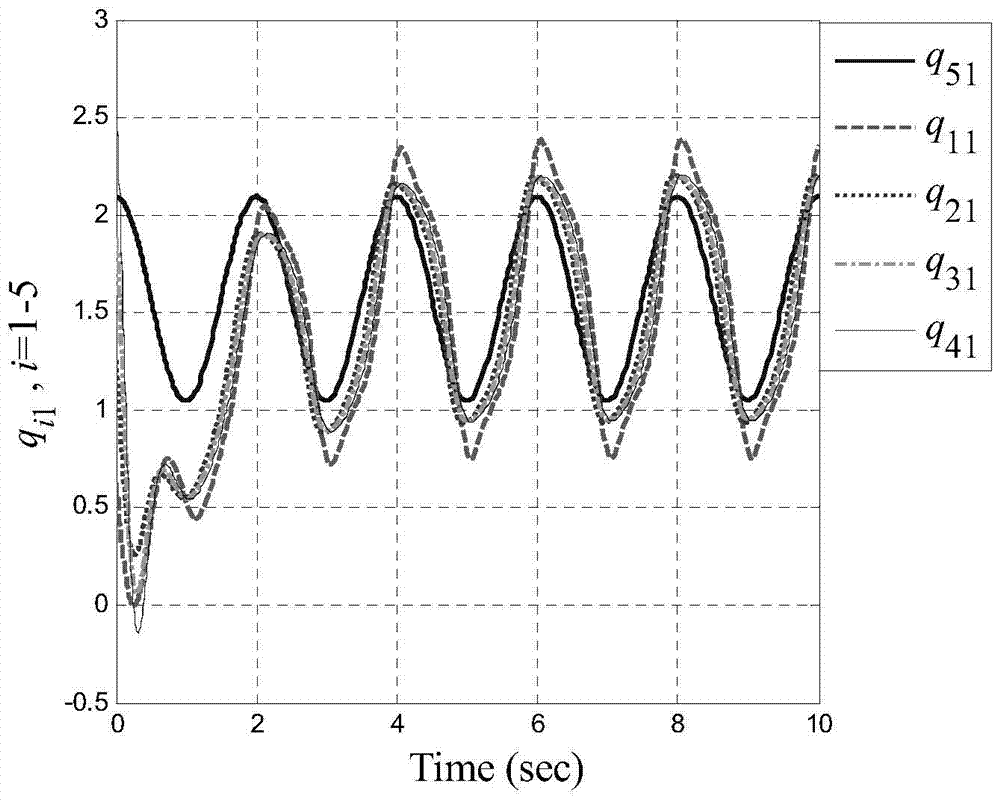
[0207] Embodiment carried out according to specific embodiment 2: a directed communication network composed of five two-degree-of-freedom manipulator robot systems, wherein numbers 1 to 4 are trackers, and number 5 is a navigator, such as figure 2 shown.

[0208] The Euler-Lagrange dynamic equation of each follower is as follows:

[0209]

[0210] where q i =col(q i1 ,q i2 ),

[0211]

[0212]

[0213]

[0214]

[0215]

[0216] J i1 ,J i2 ,m i1 ,m i2 , l i1 , l i2 represent the moment of inertia, mass and length, respectively.

[0217] The trajectory of the dynamic navigator is:

[0218]

[0219] in,

[0220] Navigator corresponds to formula The model parameters in are taken as:

[0221]

[0222] The simulation parameters take:

[0223] L=1m,m 11 =1.02kg,m 12 =1.12kg,m 21 =0.96kg,m 22 =1.15kg,m 31 =1.01kg,m 32 =1.07kg,m 41 =1.04kg,

[0224] m 42 =1.09kg,J 11 =0.21kgm 2 ,J 12 =0.42kgm 2 ,J 21 =0.23kgm 2 ,J 22 =0.39kgm 2...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention, which belongs to the robot system control field, relates to a distributed adaptive-neural-network continuous tracking control method of a multi-robot system. According to the existing coordinated tracking and controlling method of the multi-robot system, problems of parameter uncertainty and external interference existence in the multi-robot system exist. The provided method comprises: under the circumstances that only parts of followers can obtain dynamic navigator state information, a distributed observer design is implemented with limitation of communication tine delay existence, so that all followers can obtain the dynamic navigator state information; and with consideration of the parameter uncertainty and external interference existence in the system, controlling is carried out by using a distributed adaptive tracking control expression designed based on two neural networks, so that the approximate error is close to zero. In addition, the control algorithm of the distributed adaptive tracking control expression is in a continuous control mode, no buffet is caused at the system and the great practical application value is created. Besides, validity of the control algorithm is verified by the simulation experiment.

Description

technical field [0001] The invention relates to a distributed adaptive neural network continuous tracking control method for a multi-robot system. Background technique [0002] With the rapid development of modern science and technology, robot technology has been widely used in many fields such as industry, medical treatment, agriculture, and entertainment. Coordinated control of multi-robots refers to the continuous exchange of state information between multiple robots under the action of the communication network, so as to form effective control, and finally make all robots achieve regular and orderly coordinated movement. Coordinated control of multi-robots is a comprehensive subject, and its development has been recognized by academia and industry. Multi-robot coordinated control has the characteristics of high efficiency, high flexibility and high fault tolerance, and can complete tasks that cannot be completed by a single robot. In recent years, the distributed coord...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B13/04
Inventor 马广富孙延超李传江陈亮名刘萌萌王俊
Owner 成都川哈工机器人及智能装备产业技术研究院有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com