Eureka AIR delivers breakthrough ideas for toughest innovation challenges, trusted by R&D personnel around the world.

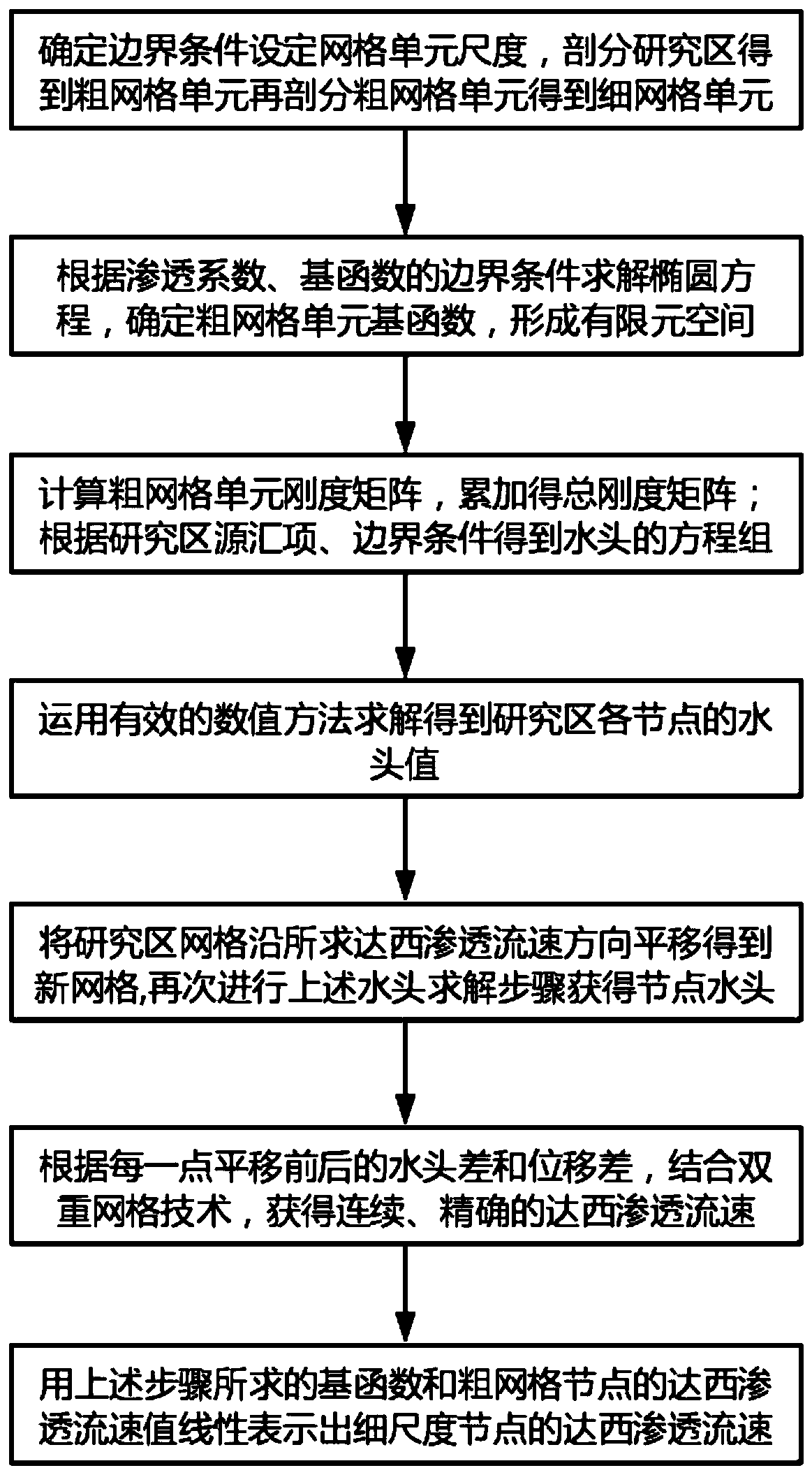
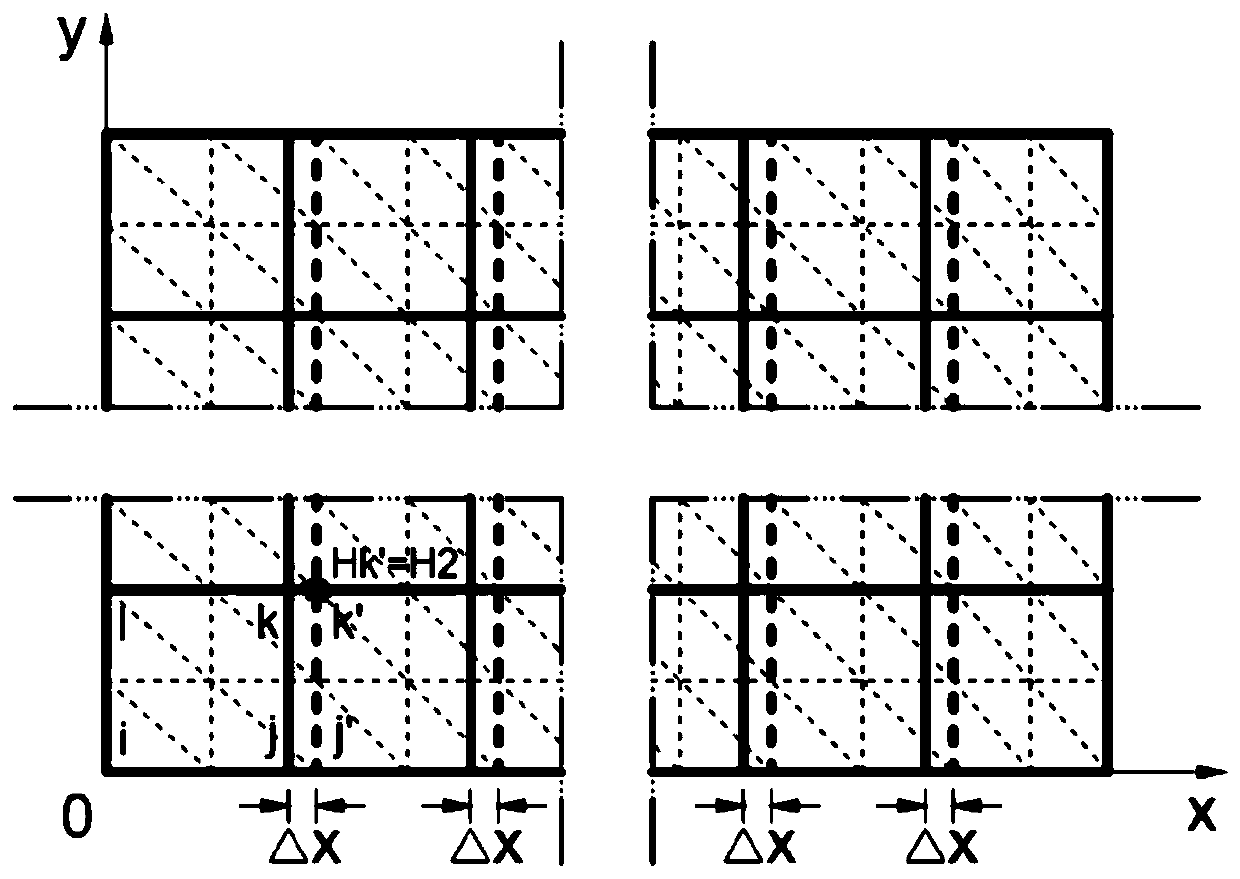
Double-grid multi-scale finite element method for simulating node Darcy permeation flow velocity

A technology for simulating nodes and finite elements, applied in the field of hydraulics, it can solve problems such as large computational consumption and low computational efficiency, and achieve the effects of high efficiency, high computational efficiency and high precision

Pending Publication Date: 2020-08-07
HOHAI UNIV +1
View PDF6 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] For above-mentioned deficiencies in the prior art, the object of the present invention is to provide a kind of dual mesh multi-scale finite element method (D-MSFEM) of simulating node Darcy seepage flow rate, to solve the traditional finite element class method in the prior art as Guaranteeing the accuracy of the solution requires a fine subdivision of the study area, resulting in a large amount of computational consumption and resulting in low computational efficiency

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Double-grid multi-scale finite element method for simulating node Darcy permeation flow velocity
  • Double-grid multi-scale finite element method for simulating node Darcy permeation flow velocity
  • Double-grid multi-scale finite element method for simulating node Darcy permeation flow velocity

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0048] Embodiment 1: two-dimensional homogeneous medium steady flow model

[0049] The research area Ω is [0, 1]×[0, 1], the aquifer thickness is 1, the permeability coefficient K=1, the analytical solution is H=xy(1-x)(1-y), the source-sink term W and The Dirichlet boundary condition is given by the analytical solution, and the two-dimensional steady flow equation for groundwater can be expressed as:

[0050]

[0051] Coarse-scale Darcy percolation velocity

[0052] In this example, the D-MSFEM, D-FEM and Yeh methods all divide the study area into N×N parts. When N=10, 20, 30 and 40, the coarse grid unit scales are 0.1, 0.05, 0.03, 0.025. When calculating with D-FEM and Yeh method, the study area is divided into 200, 800, 1800, 3200 triangular coarse mesh units (N×N×2) corresponding to them, and when calculating with D-MSFEM method, the The study area was divided into 100, 400, 900, and 1600 square coarse grid units (N×N), and each coarse grid unit was divided into 8 tr...

Embodiment 2

[0062] Example 2: Two-dimensional high oscillating head steady flow model

[0063] The two-dimensional steady flow equation for the oscillation of the permeability coefficient is (2), and the permeability coefficient The research area Ω is [0, 1]×[0, 1], the aquifer thickness is 1, the analytical solution is H=xy(1-x)(1-y), the source-sink term W and the Dirichlet boundary condition are given by The analytical solution is given. Let the amplitude A=1.99, phase Q=1.5, then the maximum value of the permeability coefficient is 400 times of the minimum value, Figure 7 This is a schematic diagram of the three-dimensional distribution of the permeability coefficient in a heterogeneous medium.

[0064] This example is solved by Yeh-F, D-MSFEM-O, D-MSFEM-L, Yeh and D-FEM methods. The coarse grid scale was set at 0.025, and D-FEM and Yeh divided the study area into 3200 triangular coarse grid units (N×N×2). D-MSFEM divides the study area into 1600 square coarse grid units (N×N), ...

Embodiment 3

[0067] Example 3: Two-dimensional gradient medium unsteady flow model

[0068] The general equation for an unsteady flow is represented by a parabolic equation in two-dimensional form:

[0069]

[0070] In the formula, K is the permeability coefficient, H is the water head, W is the source-sink item, S is the water storage coefficient, and Ω is the study area.

[0071] The study area is [0, 10km] × [0, 10km], the boundary conditions are the upper and lower water barrier boundaries, the left and right boundaries are the first type, the left boundary water head is 10m, the right boundary water head is 0m, and the source-sink item is 0. The permeability coefficient increases slowly from left to right, specifically m / day is a typical variation characteristic of the piedmont alluvial plain medium. The time step is 1day and the total time is 5day. Since there is no analytical solution for this example, the study area is finely divided into 200×200 parts by Yeh-F, and 80,000 t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a double-grid multi-scale finite element method for simulating node Darcy seepage velocity, which comprises the following steps of: dividing a research area into coarse grid units, and dividing the coarse grid units into fine grid units; obtaining a variation form of the solved problem by using a Galerkin method; constructing a primary function on each coarse mesh unit; solving a variational form by using a primary function to obtain a total stiffness matrix; obtaining an equation set of the water head according to the source confluence item and the boundary condition of the research area; solving by using an effective numerical method to obtain a water head value of each node in the research area; translating the grid of the research area for a very small distancealong the direction or the reverse direction of the obtained Darcy permeation flow velocity to obtain a translated grid; carrying out the water head solving step on the horizontally-moved grid again,and obtaininga water head; obtaining a continuous water head first-order derivative according to the water head difference and the displacement difference of each point before and after translation, and obtaining a continuous and accurate Darcy permeation flow velocity; and directly obtainingthe Darcy permeation flow velocity of a fine-scale node by applying interpolation.

Description

technical field [0001] The invention relates to the field of hydraulics, and specifically refers to a dual-grid multi-scale finite element method for simulating Darcy seepage velocity at nodes. Background technique [0002] In the numerical calculation of solute transport in groundwater aquifers, accurate and continuous Darcy seepage velocity can significantly improve the calculation accuracy of solute transport equation. Due to the limitation of the finite element framework, the traditional Darcy permeation velocity finite element algorithm must be finely divided to describe the heterogeneous medium, resulting in high calculation costs. Therefore, scientists proposed the multi-scale finite element method (MSFEM) [Hou, T.Y., and X.H.Wu(1997)] to make up for this defect. This method can capture fine-scale information through basis functions, obtain accurate solutions without fine subdivision, and has extremely high computational efficiency. In recent years, we have demonstr...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/23
Inventor 谢一凡赵文凤吴吉春鲁春辉叶逾谢春红谢镇泽
Owner HOHAI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com