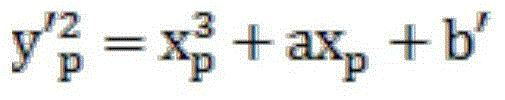Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

ECDSA method for resisting error curve attack

A curved and wrong technology, applied in the direction of user identity/authority verification, etc., can solve the problems of sacrificing the operating efficiency of the chip and getting the attackers

Active Publication Date: 2016-05-25
SHANGHAI HUAHONG INTEGRATED CIRCUIT
View PDF11 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The usual defense against the attack on the wrong curve is to check whether the point P is on the original safe elliptic curve, but the checking calculation is generally made into a function in engineering, so that the attacker may skip this step of checking by injecting burrs into the chip
In order to ensure the safety of the chip, it is necessary to check the calculation many times during the operation process, but too many checks will greatly sacrifice the operating efficiency of the chip
[0018] Therefore, if the operation point multiplied by kP is improved, after P is attacked, the attacker cannot get the correct error point product result, then the error curve attack will not succeed

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • ECDSA method for resisting error curve attack
  • ECDSA method for resisting error curve attack
  • ECDSA method for resisting error curve attack

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

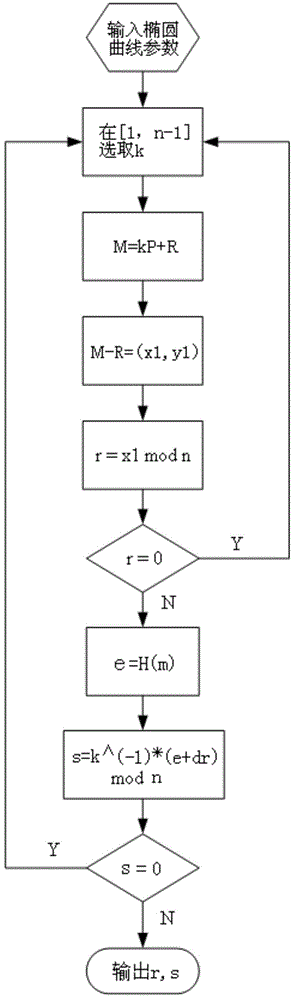
[0045] As shown in the accompanying drawings, the National Institute of Standards and Technology (NIST) of the United States recommends five sets of parameters for elliptic curve cryptography in the prime number field. One set of parameters is adopted in this embodiment, which is as follows:

[0046] In a finite field Fp, there is an elliptic curve E, which is defined as follows:

[0047] E: y 2 =x 3 +ax 2 +b

[0048] in

[0049] p = 0xffffffffffffffffffffffffffffffffffffffffffffff;

[0050] a=0xffffffffffffffffffffffffffffffffffffffffffffffc

[0051] b=0x64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1

[0052] The coordinates of the base point G are

[0053] [0x188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012, 0x07192b95ffc8da78631011ed6b24cdd573f977a11e794811]

[0054] Take point R

[0055] [0x79680B8E20EDCDB6B85D1CBFB6E83858CAA7BA83D3C3CFB3, 0xEAEF626AA6A8EA293D39ABF2FA32FC04AD3E483844B3CD07] Suppose the private key d is

[0056] d=0x79d280ca6646596b185134d44d99...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an ECDSA (Elliptic Curve Digital Signature Algorithm) method for resisting error curve attack, comprising the following steps: S1, randomly selecting k belonging to (1, n-1); S2, taking a random point R of an elliptic curve, and calculating M=R+kP; S3, calculating M-R=(x1,y1), and converting x1 into an integer; S4, calculating r=x1 mod n, and jumping back to S1 if r=0; S5, calculating e=H(m), wherein H(x) is a Hash function; S6, calculating s=k<1>(e+dr) mod n, and jumping back to S1 if s=0; and S7, outputting a signature pair (r, s). According to the invention, attackers can be effectively prevented from getting the private keys of users through error curve attack in the ECDSA.

Description

technical field [0001] The invention relates to the field of information security, in particular to an ECDSA (Elliptic Curve Digital Signature Algorithm) method for resisting error curve attacks. Background technique [0002] A theoretical introduction to the Elliptic Curve Digital Signature Algorithm (ECDSA). Digital signature corresponds to the digitization of handwritten signature, which can provide data source authentication, data integrity and non-repudiation. Elliptic Curve Digital Signature Algorithm is the elliptic curve version of digital signature. The specific process of ECDSA is as follows: [0003] Input parameter group D=(q, FR, S, a, b, P, n, h), private key d, message m. Among them, q is the order of the domain, FR is the representation of the domain, S is the seed, a, b are the parameters of the elliptic curve, P is the base point, n is the order of the point P, and h is the cofactor. [0004] Output the signature pair (r, s). [0005] Step 1. Randomly ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L9/32
Inventor 张宇
Owner SHANGHAI HUAHONG INTEGRATED CIRCUIT
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com