Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Use of birefraction borate crystal

A birefringent crystal and borate technology, applied in crystal growth, single crystal growth, single crystal growth, etc., can solve the problem of not getting valuable crystal samples

Active Publication Date: 2008-12-17
INST OF PHYSICS - CHINESE ACAD OF SCI
View PDF1 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the above-mentioned documents only synthesized powder samples, and did not obtain valuable crystal samples.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Use of birefraction borate crystal
  • Use of birefraction borate crystal
  • Use of birefraction borate crystal

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

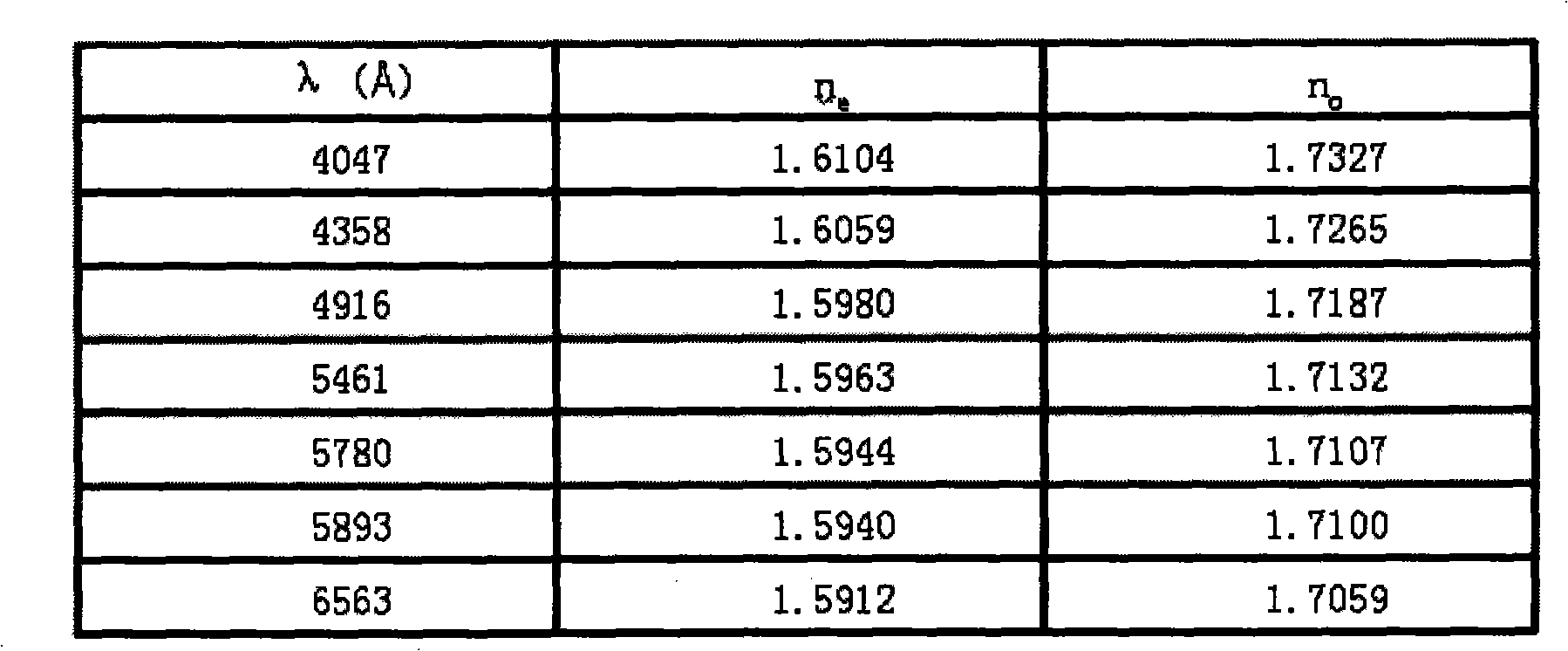
[0021] Example 1ErBa 3 B 9 o 18 Crystal Refractive Index Test

[0022] image 3 The refractive index test results of 8 different wavelengths in the visible range from violet to red are listed. The test results showed that ErBa 3 B 9 o 18 The crystal is negatively uniaxial, with a birefringence of about -0.11 in the visible wavelength range. The refractive index of violet ordinary light (404.7nm) is 1.7327, the refractive index of red ordinary light (656.3nm) is 1.7059, and its dispersion n 紫 -n 红 = 0.0268.

[0023] ErBa 3 B 9 o 18 The refractive index-dispersion equation of crystal can be expressed by the four-parameter Sellmeier equation:

[0024]

[0025] where λ is the wavelength in vacuum n is the refractive index. At 295K, the fitting results of the coefficients in the above formula are as follows Figure 4 shown. Using this equation, the refractive index value can be calculated within a certain wavelength range.

Embodiment 2

[0026] Example 2YBa 3 B 9 o 18 Crystal Refractive Index Test

[0027] Figure 5 The refractive index test results of 8 different wavelengths in the visible range from violet to red are listed. The test results showed that YBa 3 B 9 o 18 The crystal is negatively uniaxial, with a birefringence of about -0.12 in the visible wavelength range. The refractive index of violet ordinary light (404.7nm) is 1.7291, the refractive index of red ordinary light (656.3nm) is 1.7000, and its dispersion n 紫 -n 红 = 0.0291.

[0028] YB 3 B 9 o 18 Refractive Index-Dispersion Equation of Crystal: Four-parameter Sellmeier Equation

[0029]

[0030] where λ is the wavelength in vacuum n is the refractive index. At 295K, the fitting results of the coefficients in the above formula are as follows Figure 6 shown. Using this equation, the refractive index value can be calculated within a certain wavelength range.

Embodiment 3

[0031] Example 3NdBa 3 B 9 o 18 Crystal Refractive Index Calculation

[0032] The large refractive index of this series of borates comes from the group B 3 o 6 optical anisotropy. B 3 o 6 by 3 BOs 3 group constitutes, while BO 3 The polarization of the group parallel to the plane and perpendicular to the plane under the action of an external electric field is very different. According to Wooster's rule, all crystals with layered structure, if they do not contain OH groups, are crystals with negative optical axis. Please refer to the literature [Wooster, W.A. 1931, Zeit. Using Bragg's theoretical calculation on the refractive index, refer to [Ye Danian, Structural Optical Mineralogy, Geological Press, 1998] to calculate NdBa 3 B 9 o 18 Crystal Refractive Index, n e In the range of 1.58-1.62, n o In the range of 1.70-1.73, it is still a negative uniaxial crystal, and the birefringence is in the range of 0.1-0.13.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

PropertyMeasurementUnit
refractive indexaaaaaaaaaa
refractive indexaaaaaaaaaa
refractive indexaaaaaaaaaa
Login to View More

Abstract

The invention relates to an optical borate-series crystal with double refraction and application thereof. The borate-series crystal with double refraction has the chemical formula of ReBa3B9O18 (Re equals to Y, Pr, Nd, Sm, Eu, Gd, Tb, Er, Dy, Ho, Tm, Yb and / or Lu). The crystals are all uniaxial negative crystals, which have the birefringence of about 0.08 to 0.15 in the visible light band. The crystals in the series are easy to be incised, ground, polished and stored, are water immiscible, non-deliquescent and stable in air, and are suitable for being used for producing optical communication elements such as optoisolators, circulators, light beam shifters, optical polarizers and optical modulators, etc., in particular for producing polarizing prisms, phase delaying devices and electro-optical modulators with various purposes. The devices utilize the refraction index property of the optical borate-series crystal, particularly the larger birefringence (ne-no) thereof.

Description

technical field [0001] The invention relates to the field of birefringent optical crystals, in particular to a borate-based ReBa 3 B 9 o 18 Birefringent crystals (Re=Y, Pr, Nd, Sm, Eu, Gd, Tb, Er, Dy, Ho, Tm, Yb and / or Lu) and uses thereof. Background technique [0002] Birefringence is one of the important characteristics of light propagating in optical heterogeneous crystals. When light propagates in an optical heterogeneous body (such as: crystals other than cubic crystal system), except for a few special directions (along the direction of the optical axis), its vibration characteristics will be changed, and it will be decomposed into two electric field vectors. Two beams of polarized light with different propagation speeds and different refractive indices are perpendicular to each other. This phenomenon is called birefringence, and such crystals are called birefringent crystals. One of the two beams of light obeys the general law of refraction, called ordinary light ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): C30B29/22G02B1/02
Inventor 陈小龙何明王皖燕蔡格梅许燕萍刘军
Owner INST OF PHYSICS - CHINESE ACAD OF SCI
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com