Method and apparatus for performing mathematical functions using polynomial approximation and a rectangular aspect ratio multiplier
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Benefits of technology
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
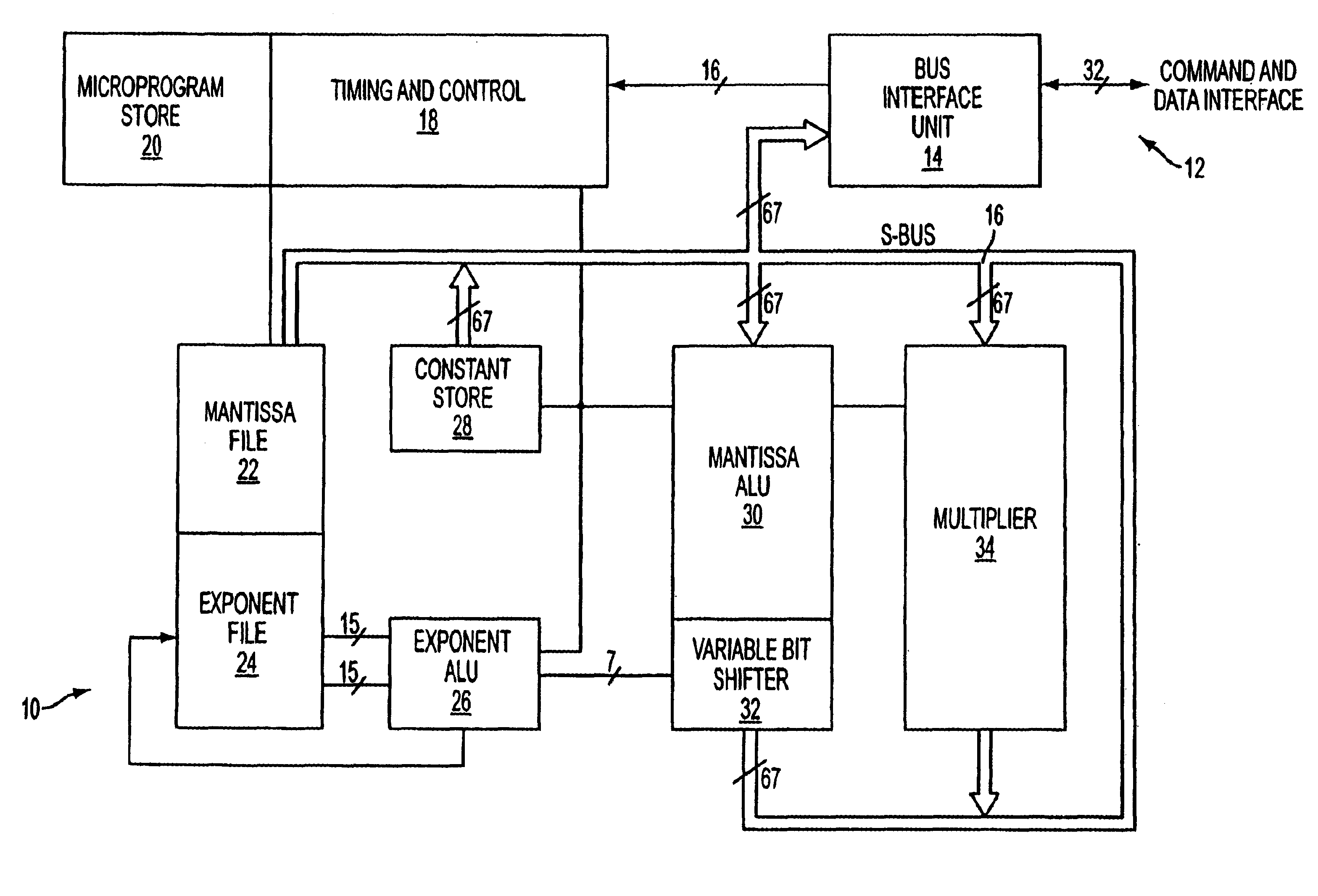
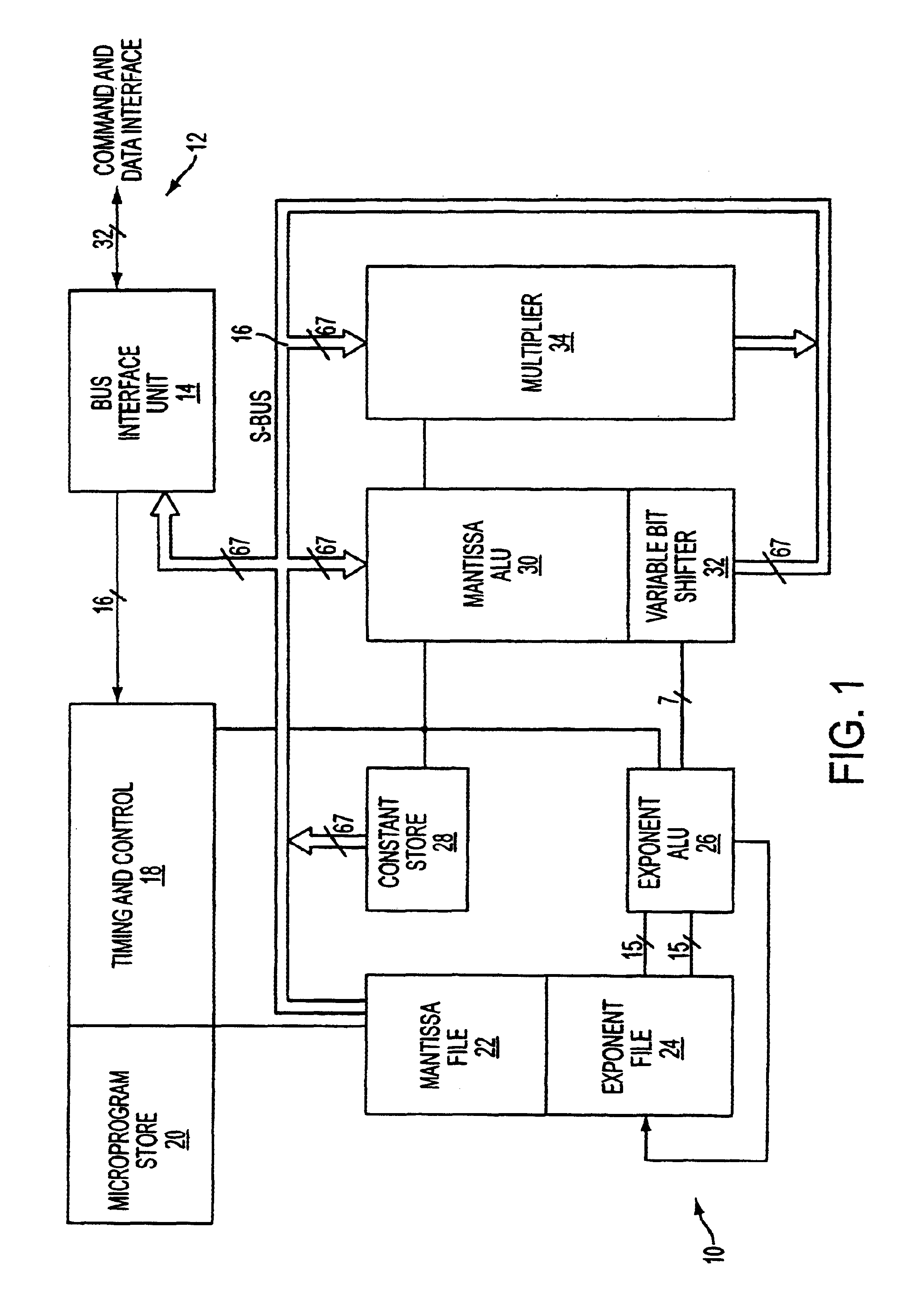
[0027]The method of calculating mathematical functions according to the present invention may be implemented in a numeric processing system which comprises a multiplier circuit with the capability to perform the primitive operations of addition, multiplication, division and the square root function.
[0028]FIG. 1 is a block diagram of an exemplary numeric processing system. FIG. 1 illustrates a system, indicated generally at 10, which interfaces with an integrated data processing system through a command and data interface indicated generally at 12. The command and data interface 12 is coupled to a bus interface unit 14 which acts to decode and route the appropriate commands and data values received from the integrated data processing system. The bus interface unit 14 is coupled to a 67-bit system bus 16 which serves to route data throughout system 10. The bus interface unit is also coupled through a 16-bit control line to a control and timing circuit 18. Control and timing circuit 18...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com