Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method of constructing check matrix for LDPC code, and encoding and decoding device of using the method

A check matrix and encoding device technology, applied in the construction field of forward error correction coding, can solve the problems of single check matrix lack of regularity, parallel processing is difficult to achieve, etc., and achieve the effects of small memory occupation, optimization, and installation

Inactive Publication Date: 2007-05-09
TIMI TECH
View PDF0 Cites 25 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This method solves the problem of storing the check matrix. Each row and column of a single check matrix lacks regularity, and parallel processing is difficult to achieve.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method of constructing check matrix for LDPC code, and encoding and decoding device of using the method
  • Method of constructing check matrix for LDPC code, and encoding and decoding device of using the method
  • Method of constructing check matrix for LDPC code, and encoding and decoding device of using the method

Examples

Experimental program
Comparison scheme
Effect test

no. 1 example

[0036] According to the first method of the present invention, a 4608*9216 dimension parity check matrix is ​​constructed.

[0037] First, get the set of common factors of 4608 and 9216, let it be F c .

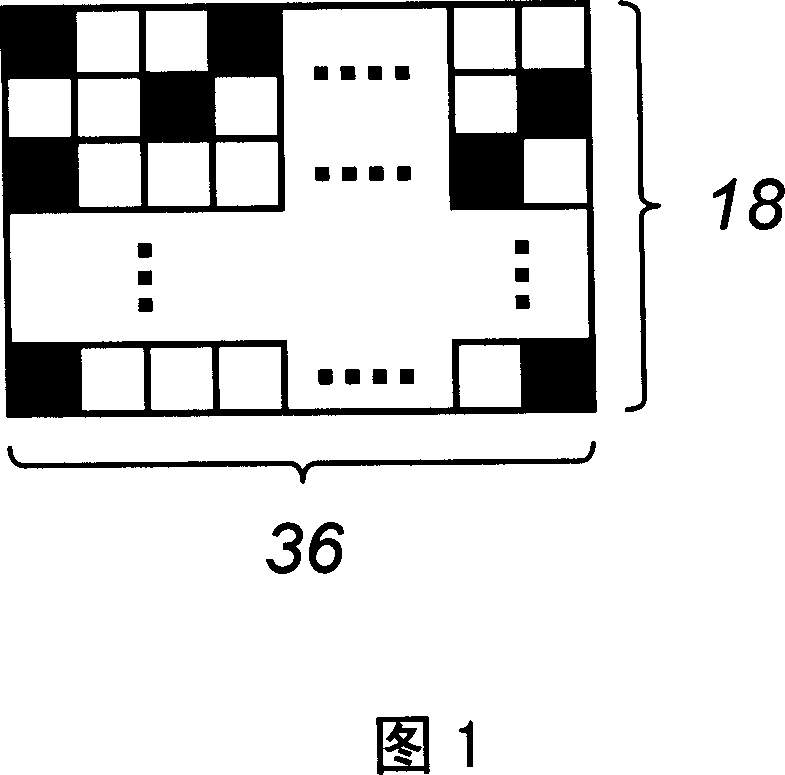
[0038] Second, choose an appropriate expansion ratio K, where K∈F c , in this embodiment, the expansion ratio is selected as a common factor of 256. In this way, the dimension of the obtained fundamental matrix is ​​18×36. The basic matrix can be generated in any way, as shown in Figure 1, where the black squares represent "1" and the white squares represent "0".

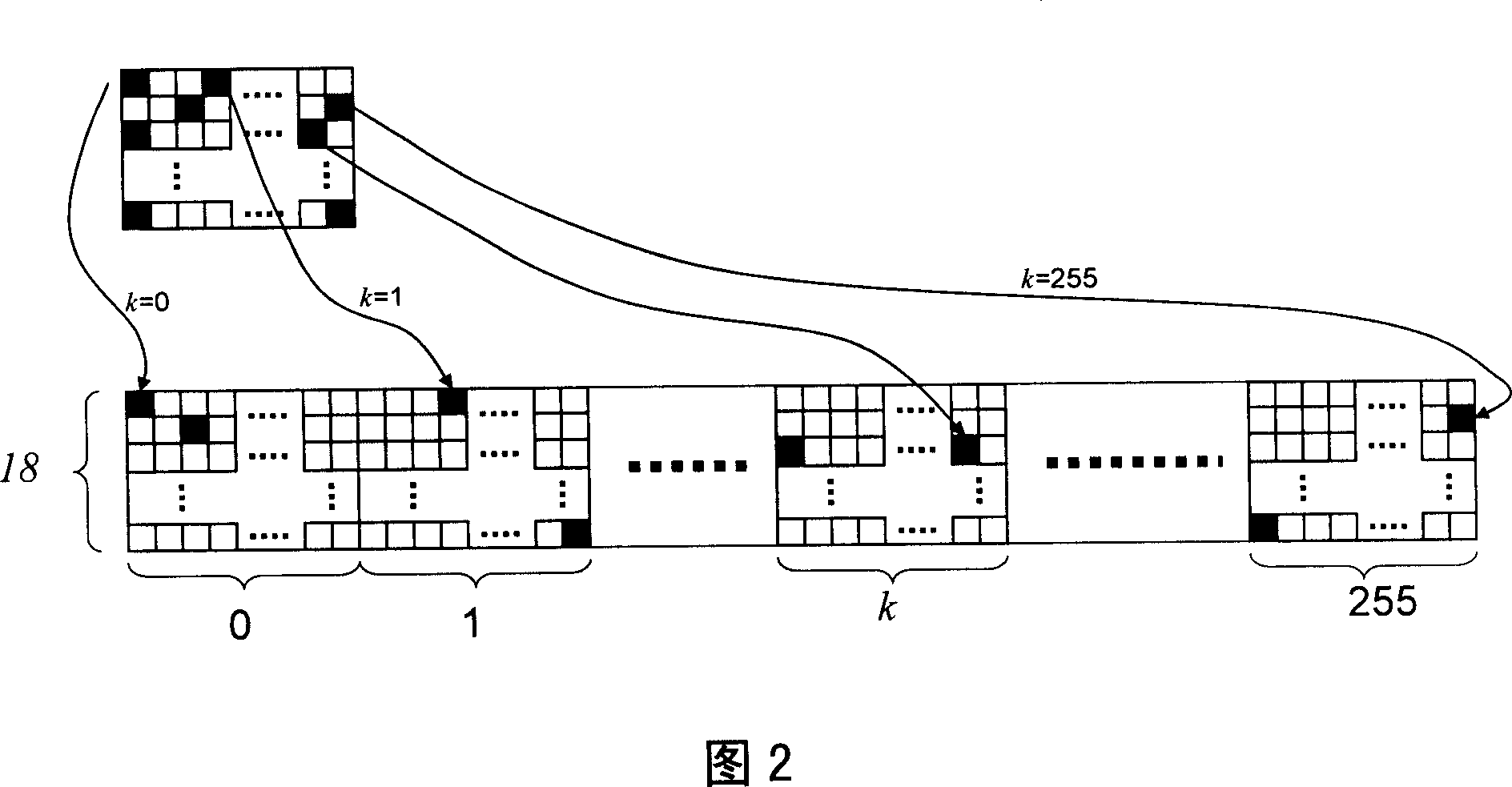
[0039] For each non-zero element in the fundamental matrix with a dimension of 18×36, select a set of different column expansion coefficients {k i , 0≤k i ≤255, i∈Z +} to expand. Specifically: set the row and column coordinates of the non-zero element as (m, n), and in (m, k i ×36+n) a "1" appears in the position, so that a 18×9216-dimensional matrix is ​​generated after expansion, as shown in Fig. 2 .

[...

no. 2 example

[0533] According to the first method of the present invention, a 2304*9216-dimensional parity check matrix is ​​constructed.

[0534] First, get the set of common factors of 2304 and 9216, let it be F c .

[0535] Second, choose an appropriate expansion ratio K, where K∈F c , in this embodiment, the expansion ratio is selected as a common factor of 256. In this way, the dimension of the obtained fundamental matrix is ​​9×36. This fundamental matrix can be generated in any way.

[0536] For each non-zero element in the fundamental matrix with a dimension of 9×36, select a set of different column expansion coefficients {k i , 0≤k i ≤255, i∈Z +} to expand. Specifically: set the row and column coordinates of the non-zero element as (m, n), and in (m, k i ×36+n) a "1" appears in the position, so that a 9×9216-dimensional matrix is ​​generated after expansion.

[0537] After column expansion, the above-generated 9×9216-dimensional matrix is ​​expanded row by row, and each r...

no. 3 example

[1021] According to another method of the present invention, a 2304*9216 dimensional parity check matrix is ​​constructed.

[1022] First, get the set of common factors of 2304 and 9216, let it be F c .

[1023] Second, choose an appropriate expansion ratio K, where K∈F c , in this embodiment, the expansion ratio is selected as a common factor of 256. In this way, the dimension of the obtained fundamental matrix is ​​9×36. This fundamental matrix can be generated in any way.

[1024] For each non-zero element in the fundamental matrix with a dimension of 9×36, select a set of different row expansion coefficients {k i , 0≤k i ≤255, i∈Z +} for expansion, where 0≤k i ≤255. Specifically: set the row and column coordinates of the non-zero element as (m, n), in (k i ×9+m, a "1" appears in the position of n), so that a 2304×36-dimensional matrix is ​​generated after expansion.

[1025] After row expansion, the 2304×36 dimensional matrix generated above is expanded column by...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The coder codes the input binary info and outputs the coded position-change system code queue. The coder consists of the matrix multiply module (MM), the compositor index module (CI) and the compositor output module (CO). MM outputs verification queue p obtained via multiplying the binary info queue m with a matrix. CI possesses N storage units and stores orderly the index value of the compositor table IDX. According to the stored index value in IDX, CO compositors against m and p, then outputs code character c. This invention uses the algebra structure to build the verification matrix of LDPC code to obtain a stable LDPC code. Besides, the coder and decoder in this invention occupy less memory units. This benefits the device optimization.

Description

technical field [0001] The present invention relates to a construction method of forward error correction coding in digital information transmission technology, in particular to a construction method of a low-density parity check (LDPC) code and an encoding device and a decoding device using the method. Background technique [0002] In 1948, Claude Shannon pioneered the famous "Noisy Channel Coding Theorem", which pointed out the maximum rate at which noisy channel information can be transmitted, that is, the channel capacity. At the same time, Shannon also deduced the limit transmission capability of the noisy channel, that is, the minimum signal-to-noise ratio required for error-free transmission of information, also known as the Shannon limit. The Shannon limit is the most important index to measure the ability of channel error correction coding. The closer the error correction coding performance curve is to the Shannon limit, the better the error correction coding perfo...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H03M13/11H03M13/19H03M13/00
CPCH03M13/1105H03M13/616H03M13/116H03M13/033H04L1/0057
Inventor 白栋刘斌彬陶涛葛启宏宋挥师李群申红兵杨庆华
Owner TIMI TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com