Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

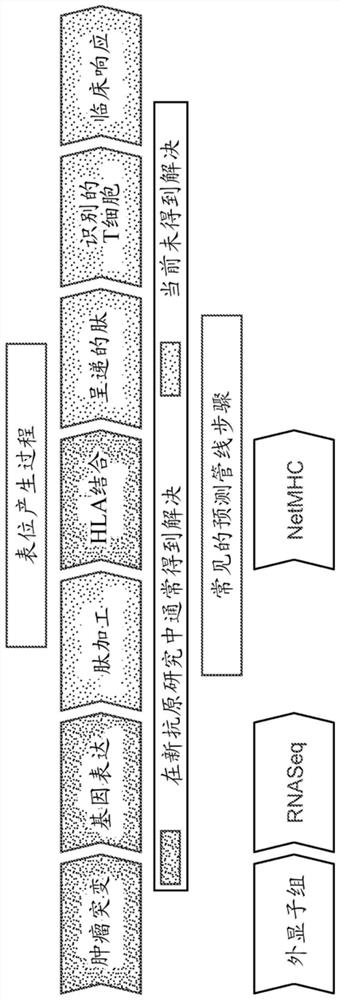
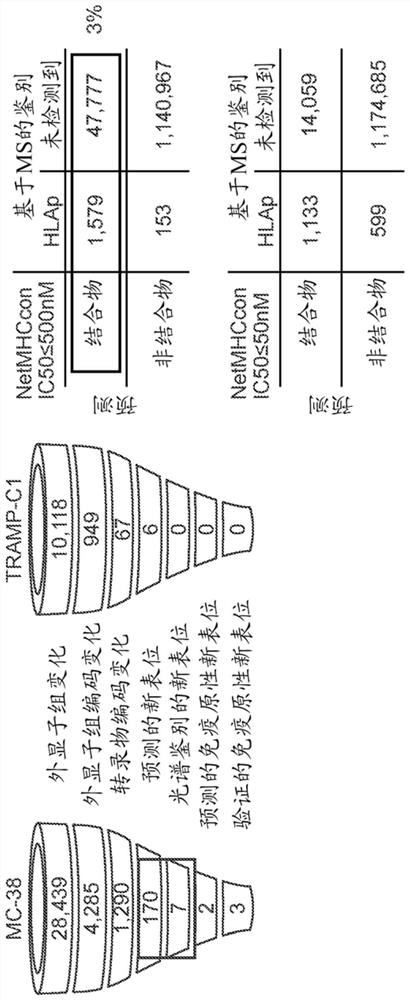
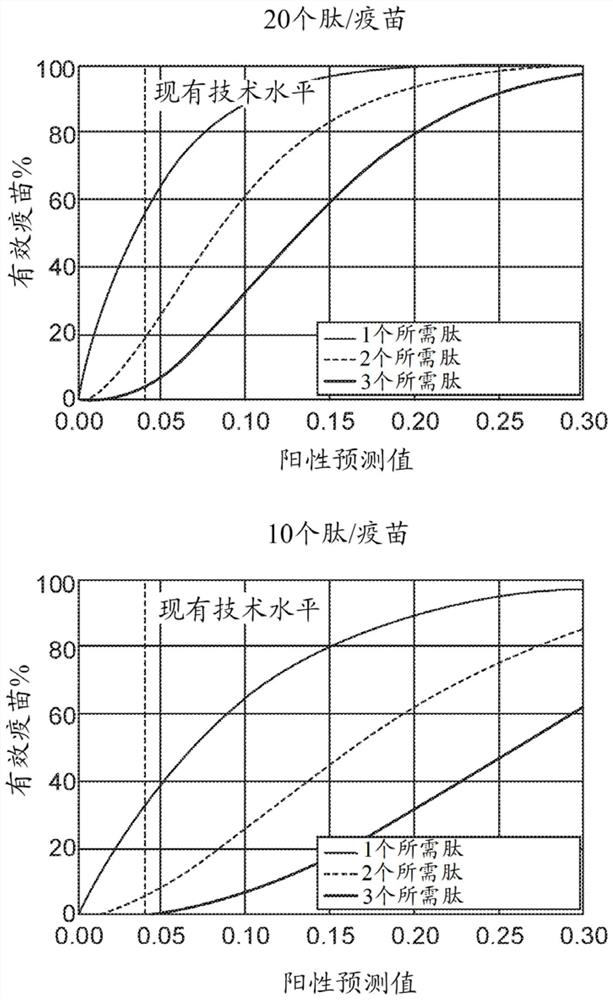
Identification of neo-antigens with mhc class ii model

A technology of antigens and models, applied in biological neural network models, antibody medical components, special data processing applications, etc., can solve the problems of missing candidate neoantigens, inefficient use of autoimmunity in vaccines, etc., and achieve the effect of speeding up the process

Pending Publication Date: 2021-11-26
GRITSTONE BIO INC
View PDF37 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0009] Finally, standard approaches to tumor genome and transcriptome profiling may miss somatic mutations that generate candidate neoantigens due to suboptimal conditions for library construction, exome and transcriptome capture, sequencing, or data analysis
Likewise, standard tumor profiling methods may inadvertently contribute to sequence artifacts or germline polymorphisms as neoantigens, leading to inefficient use of vaccine potency or risk of autoimmunity, respectively

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Identification of neo-antigens with mhc class ii model
  • Identification of neo-antigens with mhc class ii model
  • Identification of neo-antigens with mhc class ii model

Examples

Experimental program
Comparison scheme
Effect test

example

[0423] In another embodiment, the deviation parameter θ h 0 May be shared by gene families of the MHC allele h. That is, the bias parameter θ of the MHC allele h h 0 can be equal to θ 基因(h) 0 , where gene (h) is the gene family of the MHC allele h. For example, the MHC class I alleles HLA-A*02:01, HLA-A*02:02, and HLA-A*02:03 can be assigned to the "HLA-A" gene family, and these MHC alleles The respective bias parameters θ h 0 Can be shared. As another example, the MHC class II alleles HLA-DRB1:10:01, HLA-DRB1:11:01, and HLA-DRB3:01:01 may be assigned to the "HLA-DRB" gene family, and these MHC alleles Gene's respective bias parameter θ h 0 Can be shared.

[0424] Going back to equation (2), as an example, when using the affine correlation function g h (·) Of the m = 4 different MHC alleles identified, peptide p k The probability of being presented by the MHC allele h=3 can be given by:

[0425]

[0426] where x 3 k is the allelic interaction variable for t...

Embodiment 1

[0470] VIII.C.1. Example 1: Maximum of Independent Allele Models

[0471] In one embodiment, the training module 316 causes peptide p associated with a set of multiple MHC alleles H k The estimated probability of presentation u k With the probability of presentation of each MHC allele h in set H determined based on cells expressing the monoallele The variation of is modeled as described above in connection with equations (2)-(11). Specifically, the presentation probability u k can be any function of . In one embodiment, as shown in equation (12), this function is a maximum function and renders the likelihood u k can be determined as the maximum probability of presentation for each MHC allele h in set H.

[0472]

[0473] VIII.C.2. Example 2.1: The Funciton-of-Sums Model

[0474] In one embodiment, the training module 316 makes peptide p by k The estimated probability of presentation u k Modeling:

[0475]

[0476] where element a h k For the peptide seq...

Embodiment 22

[0486] VIII.C.3. Example 2.2: Functional Model Using the Sum of Allelic Non-Interacting Variables

[0487] In one embodiment, the training module 316 incorporates allelic non-interaction variables and makes peptide p by k The estimated probability of presentation u k Modeling:

[0488]

[0489] where w k Indicates the encoded related peptide p k The allelic non-interaction variable for . Specifically, the parameter set θ for each MHC allele h h and the set of parameters about the allelic non-interacting variables θ w The value of θ can be obtained by making about θ h and θ w is determined by minimizing a loss function of , where i is each instance in the subset S of training data 170 produced by cells expressing a single MHC allele and / or by cells expressing multiple MHC alleles. Correlation function g w The correlation function g introduced in Section VIII.B.3 above can be expressed as w any of the forms.

[0490] Therefore, according to equation (14), the fun...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A method for identifying T-cells that are antigen-specific for at least one neo-antigen that is likely to be presented by class II MHC alleles on surfaces of tumor cells of a subject. Peptide sequences of tumor neo-antigens are obtained by sequencing the tumor cells of the subject. The peptide sequences are input into a machine-learned presentation model to generate presentation likelihoods for the tumor neo-antigens, each presentation likelihood representing the likelihood that a neo-antigen is presented by the class II MHC alleles on the surfaces of the tumor cells of the subject. A subset of the neo-antigens is selected based on the presentation likelihoods. T-cells that are antigen-specific for at least one of the neo-antigens in the subset are identified. These T-cells can be expanded for use in T-cell therapy. TCRs of these identified T-cells can also be sequenced and cloned into new T-cells for use in T-cell therapy.

Description

Background technique [0001] Therapeutic vaccines and T cell therapies based on tumor-specific neoantigens hold great promise as the next generation of personalized cancer immunotherapy. 1–3 Cancers with a high mutational burden, such as non-small cell lung cancer (NSCLC) and melanoma, represent particularly interesting targets for such therapies, given the relatively high likelihood of neoantigen production. 4,5 Early evidence suggests that neoantigen-based vaccinations can elicit T-cell responses 6 And T-cell therapy targeting neoantigens was able to induce tumor regression in selected patients in some cases. 7 [0002] In particular, the identification of MHC class II-presented neoantigens for neoantigen-based vaccination and neoantigen-targeted T-cell therapy is a promising therapeutic because up to 50% of neoantigen-reactive TILs contain CD4 Cells that respond to neoantigens presented by MHC class II alleles. These CD4 cells have been shown to contribute to the anti-tu...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06N3/02G06F17/00A61K35/17A61K35/15A61K39/00A61K38/10C07K7/08C12N5/00
CPCC12Q1/6886G01N33/6878G01N33/56977G01N33/57484C12Q2600/136G16B40/20G16B20/00G06N3/082G06N3/08G06N3/048G06N3/044G06N3/045A61K39/464401A61K39/4632A61K39/4611G16B5/00G16B35/10G16B30/00
Inventor T·F·鲍彻B·布里克-沙利文J·巴斯比高明德M·J·戴维斯L·E·扬J·M·弗朗西斯C·帕尔默M·斯科伯恩R·耶冷斯凯
Owner GRITSTONE BIO INC
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com