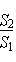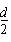Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Truncation boundary for impedance matching layer

An impedance matching and boundary technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve problems such as Cartesian coordinate calculation methods that have not yet appeared

Inactive Publication Date: 2016-05-18
TIANJIN UNIV OF TECH & EDUCATION TEACHER DEV CENT OF CHINA VOCATIONAL TRAINING & GUIDANCE
View PDF1 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At present, there is no calculation method for the absorption boundary of curved shapes in the Cartesian coordinate system

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Truncation boundary for impedance matching layer
  • Truncation boundary for impedance matching layer
  • Truncation boundary for impedance matching layer

Examples

Experimental program
Comparison scheme
Effect test

example 1

[0043] Example 1. Solve a two-dimensional problem to verify the setting of the absorption effect of the impedance matching layer. The content of the two-dimensional modeling file is: the calculated area range is (0,0)→(300,300), and the space step is Δ x =Δ y= 0.25cm, the time step is Δ t= 0.41667ps, the entire calculation area is in a vacuum state, and its conductivity is σ =0, the magnetic permeability is mu 0 , the dielectric constant is ε 0 . The point source of the time harmonic field is selected as the excitation source, and the expression is E z =sin(2 πf 0 N Δ t ), f 0 is the frequency of the source, and the number of iterations of the electromagnetic simulation is N =1050. Run the program thus, the result is as follows image 3 shown. When the point source is placed in the center of the calculation area, an obvious concentric circle diagram can be obtained. image 3 (a) and (b) show no reflection of electromagnetic waves. When the eccentric coord...

example 2

[0044] Example 2. Near-field scattering of a two-dimensional infinitely long conducting cylinder. The calculated area range is (0,0)→(250,250), and the space step is Δ x =Δ y= 0.25cm, the time step is Δ t= 0.41667ps, the conductor cylinder is located in the center of the calculation area, and its radius is 60Δ x =15cm, other areas are vacuum state. The time-harmonic plane wave source is selected as the excitation source, and the expression is E in =sin(2 πf 0 N Δ t ), f 0 Indicates the frequency of the source, and the iteration steps of the electromagnetic simulation are N =1200. Thus running the program, the result is as follows Figure 4 shown. It can be seen in the figure that the truncation boundary is a circle. Figure 4 (a) and (b) are electric fields respectively E z The phase and magnitude of , the inner square is the connecting boundary of the total field and the scattered field in the finite-difference time-domain method. Figure 4 (c) and (d) give ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a truncation boundary for an impedance matching layer, and efficient computational domain truncation is realized. The shape of a three-dimensional impedance matching layer is a spherical boundary, and 47.64% of calculated amount can be saved; the shape of a two-dimensional impedance matching layer is a circular boundary, and 21.64% of calculated amount can be saved; and the parameters of the impedance matching layer on the truncation boundary, and the number of grids of the impedance matching layer are designed. According to the truncation boundary for the impedance matching layer, example verification shows that electromagnetic waves propagated to the truncation boundary can be effectively absorbed; and in addition, the impedance matching layer can be used for a method for calculating time domain finite difference of electromagnetism, but not limited to the method.

Description

technical field [0001] The invention belongs to the technical field of computational electromagnetics software, and in particular relates to a truncated boundary calculation method for solving electromagnetic field problems, which is realized by using the principle of impedance matching. Background technique [0002] In the research of microwave circuits, antenna design, target scattering calculation and electromagnetic compatibility, the numerical calculation of electromagnetic field has been widely used. Set a truncated boundary in the calculation area, and add an absorbing layer on the boundary, which is called an absorption boundary, so that electromagnetic waves are absorbed on the truncated boundary, and the effect of a "microwave anechoic chamber" can be simulated by computer. Absorbing boundary is one of the important factors affecting the accuracy and efficiency of electromagnetic field numerical calculation. Traditional absorption boundaries are all processed in t...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50
Inventor 郑宏兴张玉贤彭升王辂万小凤邓东民
Owner TIANJIN UNIV OF TECH & EDUCATION TEACHER DEV CENT OF CHINA VOCATIONAL TRAINING & GUIDANCE
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com