Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Implementation method of multi-core parallelization of large integer multiplication ssa algorithm based on fft

A technology of large integer multiplication and implementation method, applied in the field of multi-core parallelization implementation, can solve the problems of high running time, poor running effect, high time complexity of SSA algorithm, and achieve the effect of improving running speed

Active Publication Date: 2017-07-11
INST OF SOFTWARE - CHINESE ACAD OF SCI
View PDF1 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In terms of multi-core and even many-core parallelism of large integer multiplication, researchers at home and abroad have done some work, such as literature [9] A CUDA-based large integer multiplication FFT algorithm implementation method is proposed. Compared with the SSA algorithm, the algorithm has a higher time complexity; literature [10] The author carried out parallel optimization on two platforms of multi-core and many-core respectively. Among them, the multi-core scheme related to the parallel scheme of the present invention utilizes large-scale circular convolution, which can be realized by small-scale circular convolution and negative circular convolution based on the Chinese remainder theorem. The angle of solution is optimized, but the acceleration effect is not ideal; literature [11] Based on the divide-and-conquer idea of ​​the karatsuba algorithm, the author optimizes the SSA algorithm in parallel on the GPU platform, but when the scale is greater than 4 million bits, the effect is worse than the serial operation on the 64-bit CPU platform; [12] The author realized the many-core parallelism of the traditional hand multiplication algorithm for large integers on the Intel Xeon Phi platform, but when the size is greater than 2048 bits, the running time of this method is higher than that of the GMP library; [13] The author mainly uses the Chinese remainder theorem (CRT) to achieve multi-core parallelism, but it uses the FFT algorithm with high time complexity

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Implementation method of multi-core parallelization of large integer multiplication ssa algorithm based on fft
  • Implementation method of multi-core parallelization of large integer multiplication ssa algorithm based on fft
  • Implementation method of multi-core parallelization of large integer multiplication ssa algorithm based on fft

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

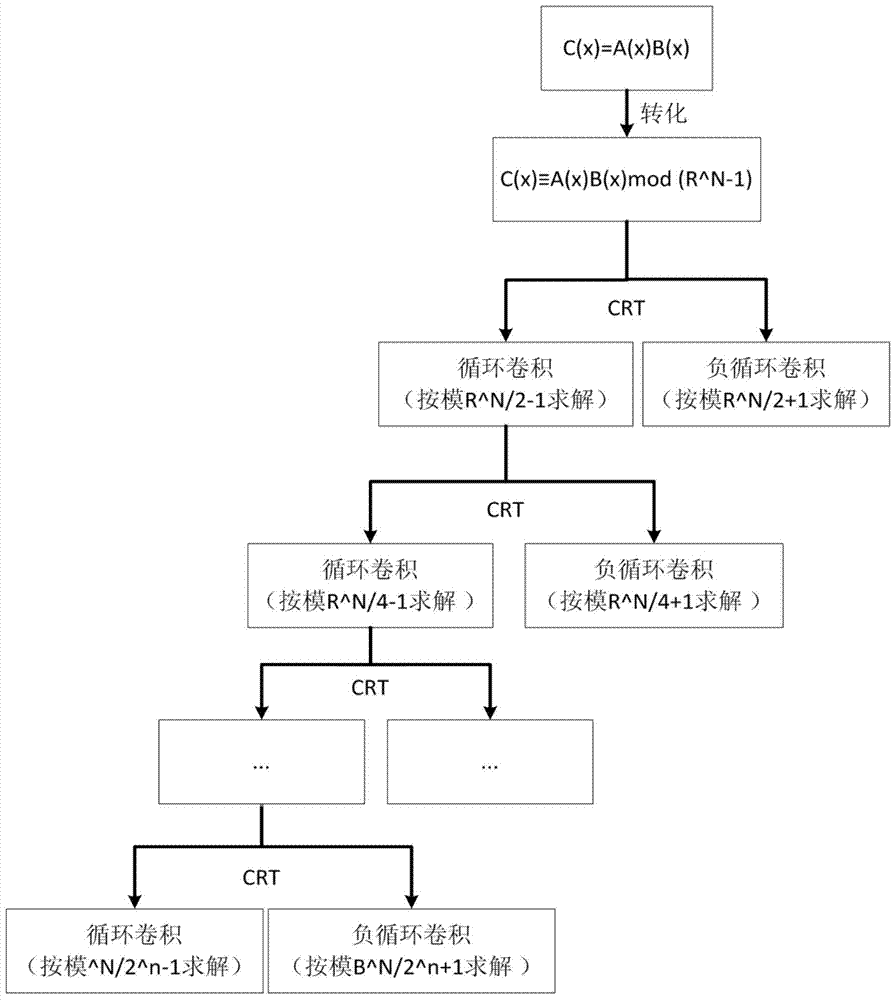
[0039] Large integers generally use base storage, and an n-bit large integer based on R can be expressed as a i (0≤i≤n-1) is 0 or a positive integer, and 0≤a i ≤R, the highest bit a n-1 ≠0. Large integers and polynomials are basically consistent in form, and large integers can be regarded as a special type of polynomial A(x), where x=R, and its value is a i (0≤i≤n-1) is an integer, and 0≤a i ≤R, the highest coefficient bit a n-1 ≠0.

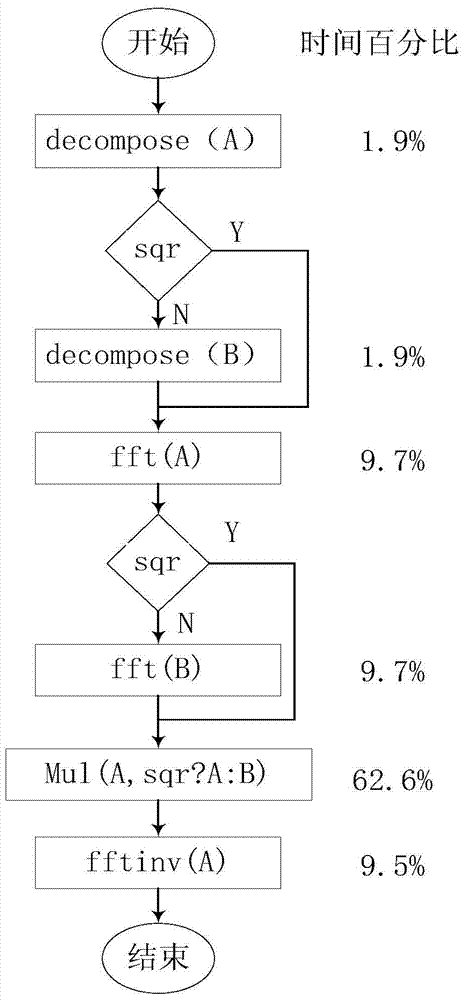
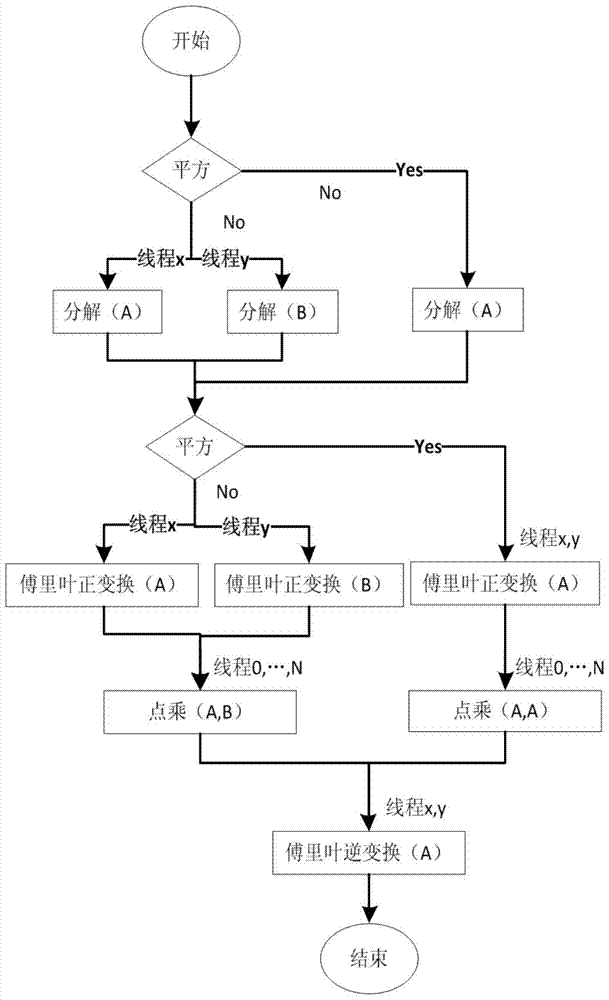
[0040] Large integers can be represented by polynomials, so the multiplication of large integers is also polynomial multiplication, and its essence is to find the convolution of two vectors. According to the convolution theorem, the discrete Fourier transform of vector convolution is the product of the vector discrete Fourier transform.

[0041] Assuming that the product of large integers a and b is to be solved, the polynomial expression of a is expressed as a i (0≤i≤n-1) is 0 or a positive integer, and 0≤a i ≤R, the highest bit a ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A multi-core parallel implementation method for large integer multiplication SSA algorithm based on FFT. It is a multi-core parallel optimization of large integer multiplication SSA algorithm from a fine-grained perspective. Its core is to use the SSA algorithm to obtain four negative circular convolution The core calculation process is designed in parallel, that is, the four calculation processes of decomposition, FFT forward transformation, point multiplication and FFT inverse transformation are respectively optimized. The invention makes full use of the multi-core resources of the hardware and improves the running speed, which plays a very important role in practical application.

Description

technical field [0001] The invention relates to a multi-core parallel implementation method for a multiplication serial algorithm based on FFT (Fast Fourier Transformation) technology in a GMP (The GNU Multiple Precision Arithmetic Library) library. Background technique [0002] In the field of information security, public key cryptosystems such as RSA and ElGamal are widely used. Modulus reduction, modular multiplication, and modular power are widely used algorithms in public key cryptosystems, and large integer multiplication is the core operation of these algorithms. Higher complexity and more time-consuming. In addition, the multiplication of large integers is also used to accurately calculate certain constants, such as the natural logarithm base e and pi, etc., as well as in the calculation of large-scale prime numbers [1] . [0003] In order to solve the problem of large number calculation, software developers and researchers from all over the world have carried out ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F9/38G06F17/14
Inventor 赵玉文刘芳芳杨超解庆春蒋丽娟
Owner INST OF SOFTWARE - CHINESE ACAD OF SCI
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com