Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Method of Attitude Control for Magnetron Bias Momentum Satellite Based on Periodic Lyapunov Equation

A technology of bias momentum and attitude control, applied in attitude control, adaptive control, general control system, etc. Saturation and other issues

Active Publication Date: 2016-08-17
哈尔滨工业大学人工智能研究院有限公司
View PDF1 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The purpose of the present invention is to solve the limitation of the magnetic torque control torque amplitude that is easily saturated and cause system instability, the limitation of the magnetic torque device control torque amplitude that the PID controller solves is not ideal and the objective function weighting matrix of the optimal control design method A method for attitude control of magnetron biased momentum satellites based on the periodic Lyapunov equation is proposed for the problem that it is difficult to establish a quantitative relationship with the performance index of the actual system

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Method of Attitude Control for Magnetron Bias Momentum Satellite Based on Periodic Lyapunov Equation
  • A Method of Attitude Control for Magnetron Bias Momentum Satellite Based on Periodic Lyapunov Equation
  • A Method of Attitude Control for Magnetron Bias Momentum Satellite Based on Periodic Lyapunov Equation

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

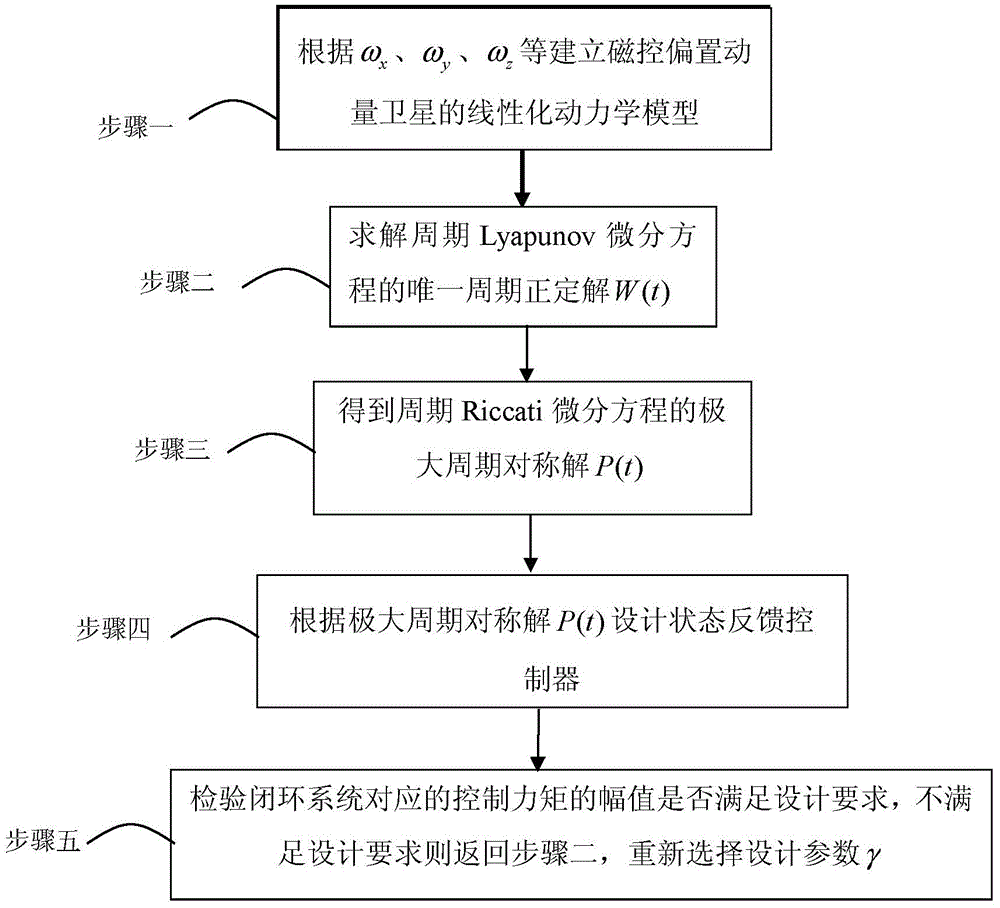
[0042] Specific embodiment one: the attitude control method of a kind of magnetron bias momentum satellite based on period Lyapunov equation of the present embodiment, specifically realize according to the following steps:

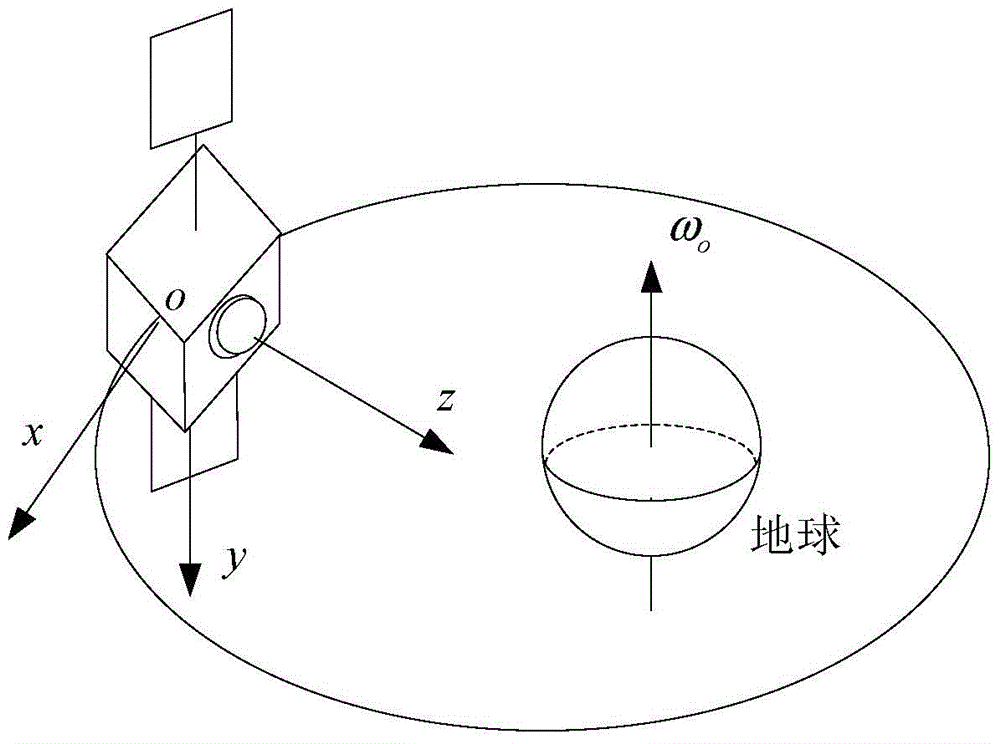
[0043] Step 1: Establish the satellite body coordinate system with the satellite center of mass as the origin o, fix the x, y and z axes on the satellite body, according to ω x , ω y , ω z Establish the linearized dynamic model of the magnetron bias momentum satellite, that is, the attitude dynamic equation of the bias momentum satellite; where the x-axis points forward along the longitudinal symmetry axis of the satellite, and the y-axis points downward perpendicular to the x-axis in the longitudinal symmetry plane of the satellite , the z-axis is perpendicular to the oxy plane, the direction of the z-axis follows the right-hand spiral rule, the x-axis is the roll axis, the y-axis is the pitch axis and the z-axis is the yaw axis; ω x , ωy , ω z is the ...

specific Embodiment approach 2

[0058] Specific embodiment two: the difference between this embodiment and specific embodiment one is that in step one, the satellite body coordinate system is established with the center of mass of the satellite as the origin o, and the x, y and z axes are fixed on the satellite body, according to ω x , ω y , ω z The specific process of establishing the linearized dynamic model of the magnetron bias momentum satellite, that is, the attitude dynamic equation of the bias momentum satellite, is as follows:

[0059] I ω · + ω × ( Iω + h ) = - h · + T

[0060] In the formula, ω=[ω x ω y ω z ] T is the rotational angular velocity of the satellite body coordinate system relative to the geocentric inertia coordinate system, is the change rate of...

specific Embodiment approach 3

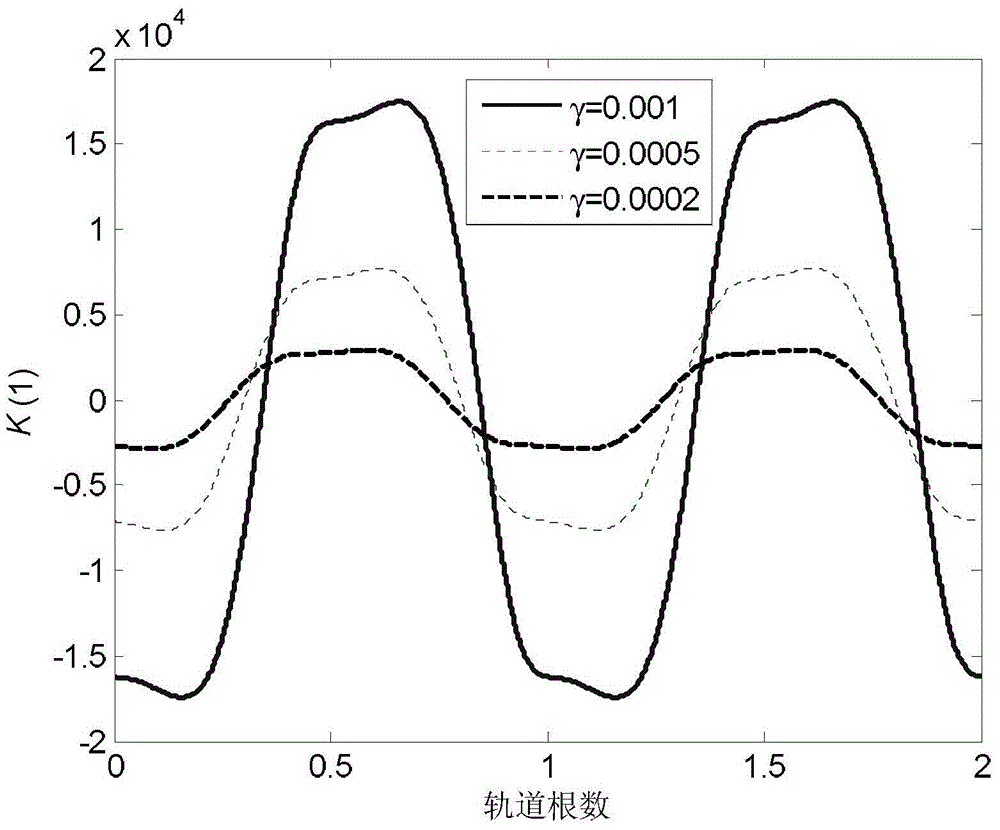
[0093] Specific embodiment three: what this embodiment is different from specific embodiment one or two is: select design parameter γ in step 2, i.e. scalar function γ, the specific process of solving periodic Lyapunov differential equation is:

[0094] (1), the periodic Lyapunov differential equation is:

[0095] W · ( t ) = W ( t ) A T + AW ( t ) + γ ( t ) W ( t ) - B ( t ) R - 1 ( t ) B T ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an attitude control method of a magnetic control bias momentum satellite based on a periodic Lyapunov equation, and the invention relates to a magnetic control bias momentum satellite attitude control system. The present invention is to solve the problem that the magnitude of the magnetic control torque is limited and the selection of the weighting matrix of the traditional optimal control design method is difficult to establish a quantitative relationship with the performance index of the actual system, and a magnetic control bias based on the periodic Lyapunov equation is proposed. Attitude control method for momentum satellites. The method is through 1. Establishing a linearized dynamic model of the magnetron bias momentum satellite attitude control system; 2. Solving the symmetric positive definite solution W(t) of the periodic Lyapunov differential equation; 3. Obtaining the symmetric positive definite solution of the periodic Riccati differential equation P(t); 4. Get the state feedback controller; 5. Check the control effect and the amplitude of the control torque. The invention is applied to the field of attitude control of magnetic control bias momentum satellites.

Description

technical field [0001] The invention relates to an attitude control method of a magnetron bias momentum satellite based on a periodic Lyapunov equation. Background technique [0002] The magnetic control bias momentum system has many excellent characteristics and is widely used in satellite attitude control. On the one hand, the magnetic control torque uses the earth's magnetic field to generate control torque. As a semi-passive actuator, it can support the satellite's long-term operation; on the other hand, the bias momentum system does not require a yaw attitude sensor, making the satellite structure Simple, low cost, and high reliability. Attitude stabilization control of magnetron bias momentum satellites has been the focus of research at home and abroad. [0003] The magnetic torque of a certain type of magnetic torque device is fixed, so the amplitude of the control torque that the magnetic torque device can provide is limited. The boundedness of the control signal ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05D1/08G05B13/04
Inventor 周彬刘少兵
Owner 哈尔滨工业大学人工智能研究院有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com