Spatial rotation mechanism gravity unloading device and method based on Kalman filtering
A technology of Kalman filtering and rotating mechanism, which is applied to simulation devices of space navigation conditions, transportation and packaging, space navigation equipment, etc., can solve the problems of complex control system, increased system cost, and cumbersome mechanical structure, and achieves elimination of mixed noise. , the effect of high unloading accuracy and fast tracking
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
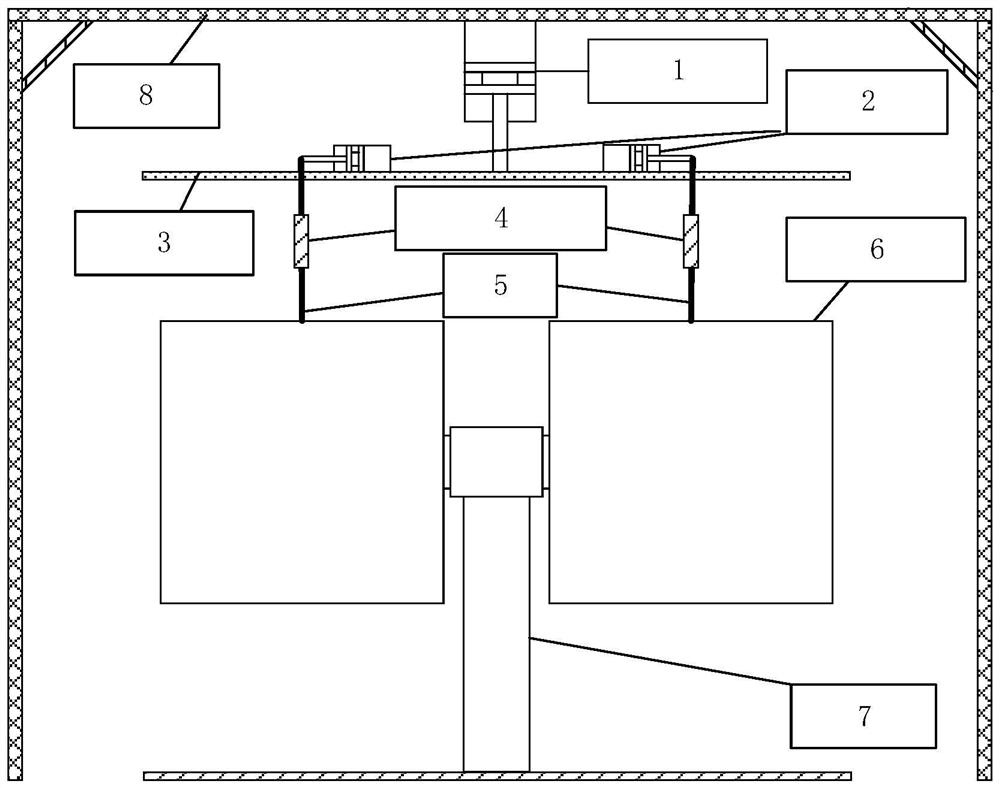
[0066] Example 1: as Figure 1-2 As shown in the figure, a Kalman filter-based gravity unloading device and method for a spatial rotating mechanism involved in this embodiment, the Kalman filtering-based gravity unloading device for a spatial rotating mechanism is composed of a servo motor, a Z-axis motor, a rotating platform, a tension sensor, Suspended wire, turntable load, turntable, truss, etc. The T-type turntable can drive the load to move in two degrees of freedom, pitch and yaw. The servo motor performs real-time angle tracking on the yaw movement of the turntable through the position encoder located on the yaw axis of the turntable, so that the unloading of the turntable load can be suspended. Always maintain the vertical state; at the same time, the suspension wire tension value calculated by the planned unloaded load gravity is used as the control command of the Z-axis motor, and the suspension wire tension is always maintained with the Z-axis motor control command ...
Embodiment 2
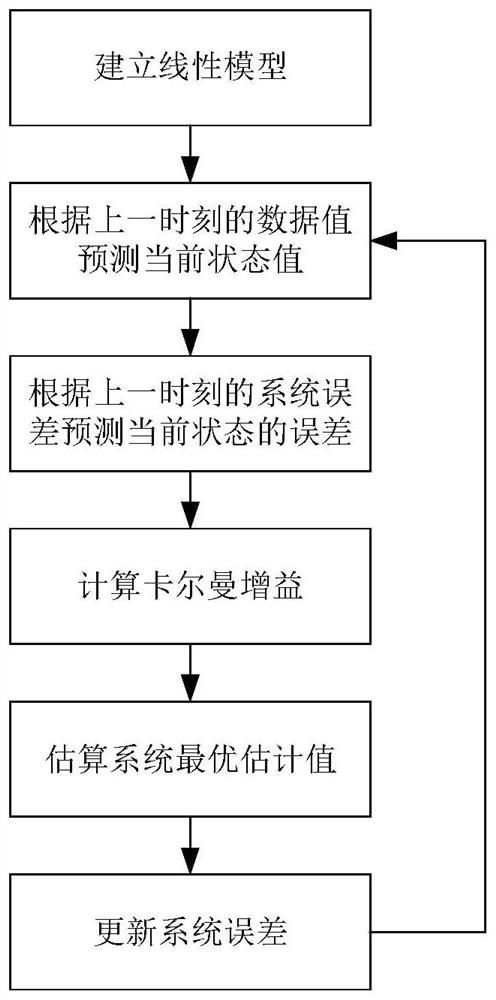
[0072] Embodiment 2: as figure 2 As shown, for a method for gravity unloading of a space rotating mechanism based on Kalman filtering involved in this embodiment, in order to describe the Kalman filtering algorithm, it is assumed that there is a linear system described by the following differential equation.
[0073] x(k)=Ax(k-1)+Bu(k)+w(k) (1)
[0074] z(k)=Hx(k)+v(k) (2)
[0075] x(k) and x(k-1) represent the state variables at the kth time and the k-1th time, u(k) represents the control amount of the input of the whole system at the kth time, z(k) is It represents the value obtained by the system from the sensor at the kth time. The three coefficients A, B, and H represent the state matrix, control matrix and measurement matrix, respectively. w(k) in equations (1) and (2) ,v(k) is generally used as white Gaussian noise as the interference of the whole system, and their covariance is generally represented by Q, R in equation (4) and equation (5).
[0076] Once we have th...
Embodiment 3
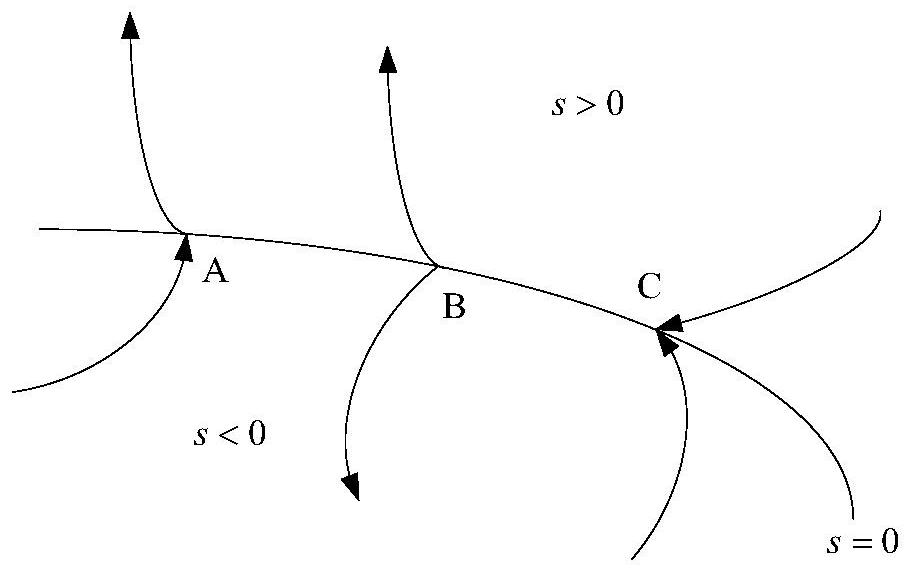
[0088] Example three: as figure 1 and 3 As shown, the present embodiment involves a method for unloading the gravity of a space rotating mechanism based on Kalman filtering, and a method for controlling the constant tension of a suspended wire:
[0089] Aiming at the elastic deformation of the suspension wire, the small torsion and the model nonlinearity caused by the servo motor, the unknown model parameters, etc., and because the sliding mode control has strong robustness, it is extremely insensitive to parameter perturbation and external interference. The design process of the control law is simple, and the sliding mode control is proposed to lock the tension of the suspension wire.
[0090] First we need to give the mathematical definition of sliding mode variable structure control. Consider an arbitrary nonlinear system expressed as:
[0091]
[0092] For the state space of the system shown in Eq. (8), there is a sliding mode surface
[0093] s(x)=s(x 1 ,x 2 ,…,x...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com