Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Adiabatic shortcut method for high-fidelity population inversion in two-energy-level system

A population number and high-fidelity technology, applied in the field of quantum computing, can solve the problems of poor robustness and long evolution time, and achieve the effect of good robustness, short evolution time and high fidelity

Pending Publication Date: 2019-08-13
SHANGHAI UNIV
View PDF4 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to solve the technical problems of too long evolution time and poor robustness, and provide an adiabatic shortcut method for high-fidelity population inversion in a two-level system

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Adiabatic shortcut method for high-fidelity population inversion in two-energy-level system
  • Adiabatic shortcut method for high-fidelity population inversion in two-energy-level system
  • Adiabatic shortcut method for high-fidelity population inversion in two-energy-level system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0035] An adiabatic shortcut method for high-fidelity population inversion in two-level systems, according to the initial state of the system and final state polynomial Fit theta and beta:

[0036] θ(t)=a 0 +a 1 t+a 2 t 2 +a 3 t 3 ,

[0037] β(t)=b 0 +b 1 t+b 2 t 2 +b 3 t 3 ,

[0038] Where θ is in the range of [0, π], and β is in the range of [0, 2 π]. Adiabatic shortcut technology based on the Lewis-Riesenfeld quantum invariant theory is used to inversely solve the time-dependent Schrödinger equation of the two-level system to obtain the pulse signal. The obtained pulse signal is input to an arbitrary wave generator to generate pulses applied to the electrodes of the gallium arsenide / gallium aluminum arsenide heterogeneous crystal circle.

[0039] Such as figure 1 Shown are the images of pulsed signals Δ and Ω generated by this technical scheme. It can be seen from the image that the curve is smooth enough to be easily obtained in the experiment. The p...

Embodiment 2

[0044] This embodiment is basically the same as Embodiment 1, and the special feature is that in this embodiment, trigonometric functions are used to fit θ and β:

[0045]

[0046] β(t)=ArcCot(0.1t f θ'(t))

[0047] Generated pulse signal see Figure 4 , Figure 4 It can be seen that the curve is smooth enough to be easily obtained in experiments. The pulse action time is still 1ns.

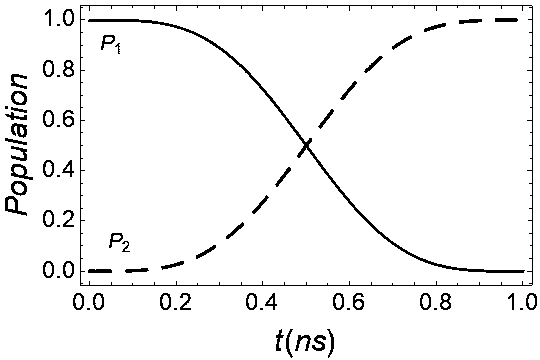
[0048] Such as Figure 5 Shown is a graph of the population number evolution over time. From the evolution image of the population number, it can be seen that this method makes the population number of the two-level system change from the initial state evolved to the end state Successfully realized the inversion of the population number.

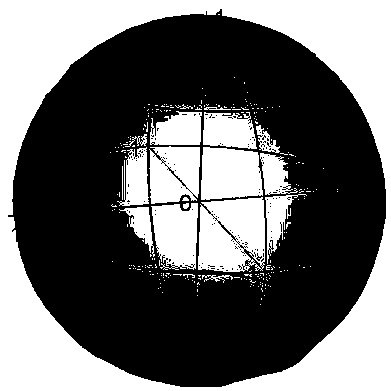
[0049] Such as Figure 6 Shown is the evolution trajectory of the system on the Bloch sphere. by comparison image 3 , we can find that by using different functions to fit θ and β, we get different system evolution trajectories that realize popula...

Embodiment 3

[0051] This embodiment is based on the first embodiment, considering the influence of two-level phase noise and decoherence. The main equation of the system is expressed in the form of Lindblad equation as:

[0052]

[0053] where γ is the decoherence rate, ρ and σ i are the density matrix and the Pauli matrix, respectively.

[0054] The pulse signal adopted in this embodiment is the same as that in Embodiment 1, see figure 1 .

[0055] Fidelity F=|f )>|. At the decoherence rate γ=7×10 6 the s -1 , the fidelity F=94.56%. For the evolution trajectory of the system on the Bloch sphere, see Figure 7 ,From Figure 7 We can see that the system still evolves from the north pole of the Bloch sphere to the south pole, that is, the inversion of the population number has been realized, but due to the influence of phase noise and decoherence, it has not completely evolved to the Bloch sphere The south pole of (0,0,-1).

[0056] Such as Figure 8 Shown is to generate the ta...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a heat insulation shortcut method for high-fidelity population inversion in a two-energy-level system. A time-containing schrodinger equation of a two-energy-level system by adopting an inverse control method based on Lewis-Riesenfield quantum invariants; a group of pulse signals capable of achieving population inversion of the two-energy-level system are constructed, an arbitrary wave generator is used for generating the pulse signals, and therefore the population inversion is achieved in a high-fidelity mode within a short action time. On the premise that the Ratio frequency of a generated pulse signal does not exceed 15GHz, inversion of the population number of a two-level system can be achieved within the action time of 1ns, the fidelity is not lower than 92% under the influence of phase noise and decorrelation, and the fidelity is not lower than 99.85% within the frequency detuning amount range.

Description

technical field [0001] The invention belongs to the field of quantum computing, and in particular relates to an adiabatic shortcut method for high-fidelity population number inversion in a two-energy level system. Background technique [0002] Under the time-dependent interaction field, the effective manipulation and preparation of quantum states has always been a main goal of people's research, and has extremely wide applications. For example, in the diffraction and interference of nuclear magnetic resonance and related spectrum technology, as well as the rapidly developing quantum information and quantum computing, it has very important application and research value. [0003] In the above-mentioned fields, the two-level system model is a ubiquitous basic model, and it is the basic structural unit that constitutes other more complex multi-level systems. Transition is a very important quantum state manipulation. This control requires high speed, high fidelity, and stabili...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H03K5/26G06N10/00G06F17/13G06F17/15
CPCG06F17/13G06F17/15G06N10/00H03K5/26
Inventor 班玥周俊陈玺
Owner SHANGHAI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com