Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

An unmanned aerial vehicle relay control system based on an efficient low-complexity LDPC code

An LDPC code, low-complexity technology, applied in the field of UAV relay command and control system, can solve the problems that hinder the large-scale use of UAVs, large transmission loss, channel congestion, etc.

Inactive Publication Date: 2019-06-21
CHENGDU UNIV
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At the same time, this type of chip is monopolized by companies such as TI and AD in the United States, and it is extremely unlikely to do customized secondary development for the dedicated data link network between drones and radio stations.
[0004] However, the UAV relay station designed based on the 802.1x chip has obvious product homogeneity and irreparable defects: ① low power, generally below 100mW; ② repetition frequency, concentrated at 2.4G Or 5.8G, the channel is crowded, and the transmission information is susceptible to interference; ③The networking mode is fixed and cannot be changed, and it can only be based on the TCP / IP network, which is not applicable to the dedicated data link network between the drone and the ground station; ④The frequency band is high, It leads to large transmission loss, and the general control distance does not exceed 1000 meters, which seriously hinders and inhibits the wide-scale use of UAVs in many aspects; Large, low reliability of information transmission

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • An unmanned aerial vehicle relay control system based on an efficient low-complexity LDPC code
  • An unmanned aerial vehicle relay control system based on an efficient low-complexity LDPC code
  • An unmanned aerial vehicle relay control system based on an efficient low-complexity LDPC code

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

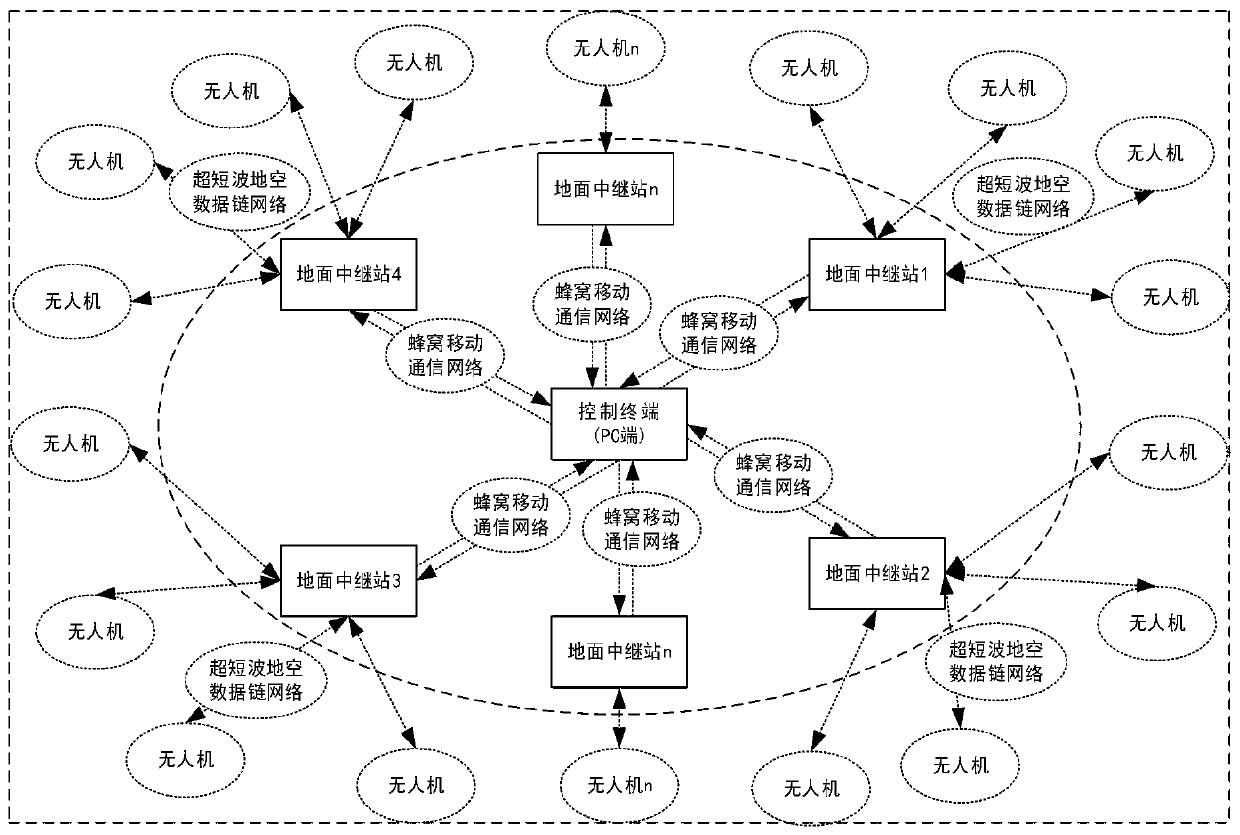
[0073] This embodiment provides an unmanned aerial vehicle relay command and control system based on high-efficiency and low-complexity LDPC codes. Temporary communication support and some areas of military activities can solve the previous limitation that UAVs and controllers must be in the same area, and can also improve the high-speed, accurate and reliable transmission of control information. UAV controllers can also use cellular mobile networks in different places. Transmission control to achieve real-time monitoring, directing the flight of UAVs, and obtaining various information captured by UAVs, and solving the problem of controlling UAVs in different places.

[0074] Specifically, such as figure 1 As shown, the UAV relay command system based on high-efficiency and low-complexity LDPC codes includes:

[0075] The control terminal is used to send control instructions to the UAV through the repeater, and receive the situation information of the UAV decoded and demodulat...

Embodiment 2

[0082] Based on the realization of Embodiment 1, this embodiment provides an unmanned aerial vehicle relay control system based on high-efficiency and low-complexity LDPC codes, and further discloses specific implementations of the codes.

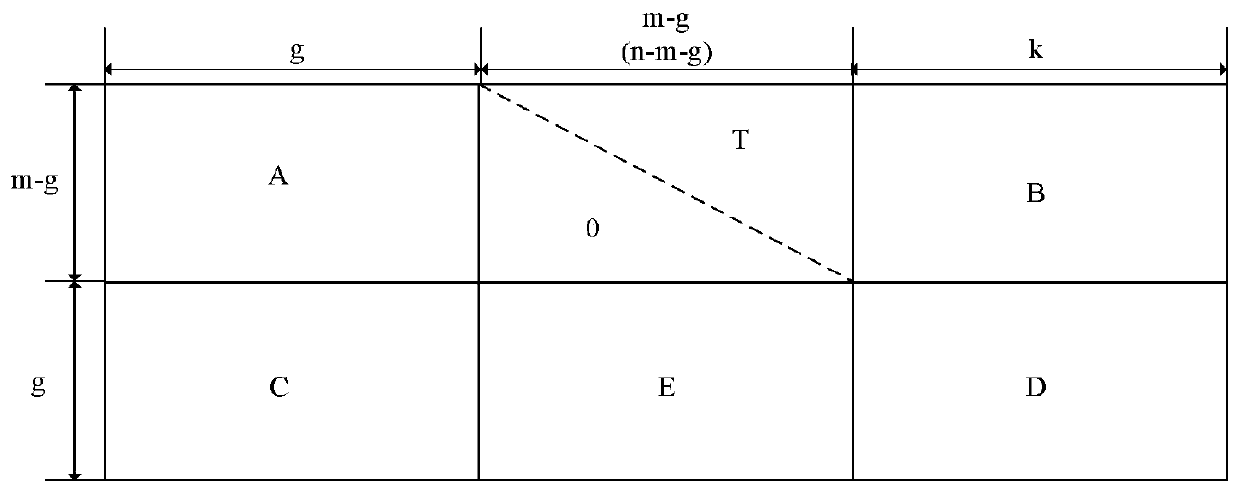
[0083] Firstly, the standard LDPC coding in the prior art is described, assuming that the code length of the LDPC code is n, the coding code word is c, the information code length is k, the information code word is u, and the check code length is m=n-k. Check matrix H can be reduced to:

[0084] H=[P m×k I m×m ]

[0085] In the formula: P m×k is a binary matrix of m×k, I m×m is an m×m identity matrix. By the calibration equation G·H T = 0 to get the generating matrix:

[0086] G = [I k×k P T k×m ]

[0087] The encoded codeword c can be obtained by c=u·G. If the coding rate R=k / n, then it can be known that the number of multiplications for coding a frame is k·n=R·n 2 , the number of additions is (k-1)·n=R·(n-1 / (2R)) 2 -1 / (4R). ...

Embodiment 3

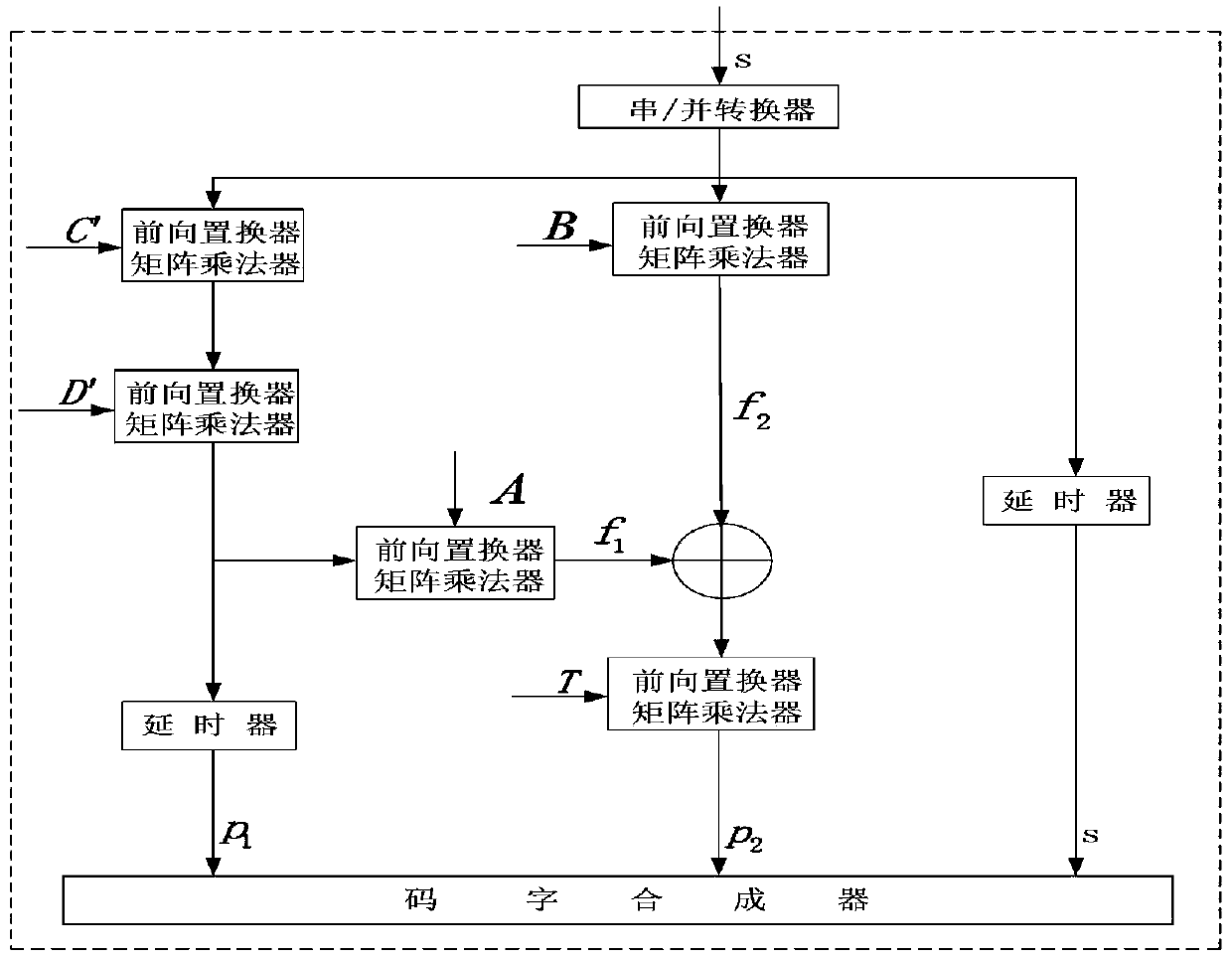
[0111] Based on the realization of Embodiment 1, this embodiment provides an unmanned aerial vehicle relay control system based on high-efficiency and low-complexity LDPC codes, and further discloses the specific implementation of decoding.

[0112] Specifically, in the prior art, the decoding algorithms of LDPC codes are divided into hard-decision decoding algorithms and soft-decision decoding algorithms, and the basis of the soft-decision decoding algorithms is the Belief Propagation Algorithm (BP). Each iteration of the BP algorithm includes two steps: the processing of the check node and the processing of the variable node. The message of the BP algorithm is usually expressed in the form of probability, and it can also be expressed in the form of logarithmic likelihood ratio. The logarithmic likelihood ratio of BP algorithm Compared with the probability domain BP algorithm, the biggest advantage is that it converts a large number of multiplication operations into addition o...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an unmanned aerial vehicle relay control system based on an efficient low-complexity LDPC code. The unmanned aerial vehicle relay control system comprises a control terminal; arelay station which is connected with the control terminal through a cellular mobile communication network, and is used for transcoding the received control instruction into formatting control information which can be received by the unmanned aerial vehicle, carrying out processing including modulation, coding, error correction, verification and signal amplification, and then sending the formatted control information to the unmanned aerial vehicle airborne radio station through an external ultra-short wave antenna; The relay station is also used for receiving the information from the unmannedaerial vehicle airborne radio station, decoding and demodulating the binary bit information, transcoding the binary bit information into a signal conforming to a cellular communication mobile networkformat, and sending the signal to the control terminal; and an unmanned aerial vehicle. According to the method, the unmanned aerial vehicle is remotely and remotely controlled through full use of the cellular mobile network, the reliability and effectiveness of data transmission are improved, efficient encoding and decoding processing is carried out on transmitted information, the unmanned aerial vehicle is comprehensively used in multiple aspects, and the unmanned aerial vehicle is put into all industry fields of the society as much as possible.

Description

technical field [0001] The invention relates to an unmanned aerial vehicle relay command system based on high-efficiency and low-complexity LDPC codes. Background technique [0002] At present, the research and development of UAV relay radio system at home and abroad is basically in a blank state, and most of the operation and application of UAV are still in the traditional man-machine co-location mode. [0003] Some large enterprises and institutions at home and abroad have developed some military UAV radio stations, but due to the particularity of their industry (military purpose), their functions are often focused on pursuing large bandwidth and high performance, and less consideration is given to cost and power consumption , quantity and other factors, large-scale application will have many restrictions. The relay mode of this part of military drone radio generally does not use civilian cellular network as the medium of extending distance, but adopts the formula of micr...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L1/00H04B7/185H03M13/11
Inventor 廖雄马溧溧罗正华张子嬛睢超亚康腾飞贺昌兵
Owner CHENGDU UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com