First-order perturbation expansion progressive homogenization method for statistical prediction of elastic constitutive matrix of random distributed composite materials
A composite material, random distribution technology, applied in the field of asymptotic homogenization of statistical first-order perturbation expansion for the prediction of elastic constitutive matrix of randomly distributed composite materials
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
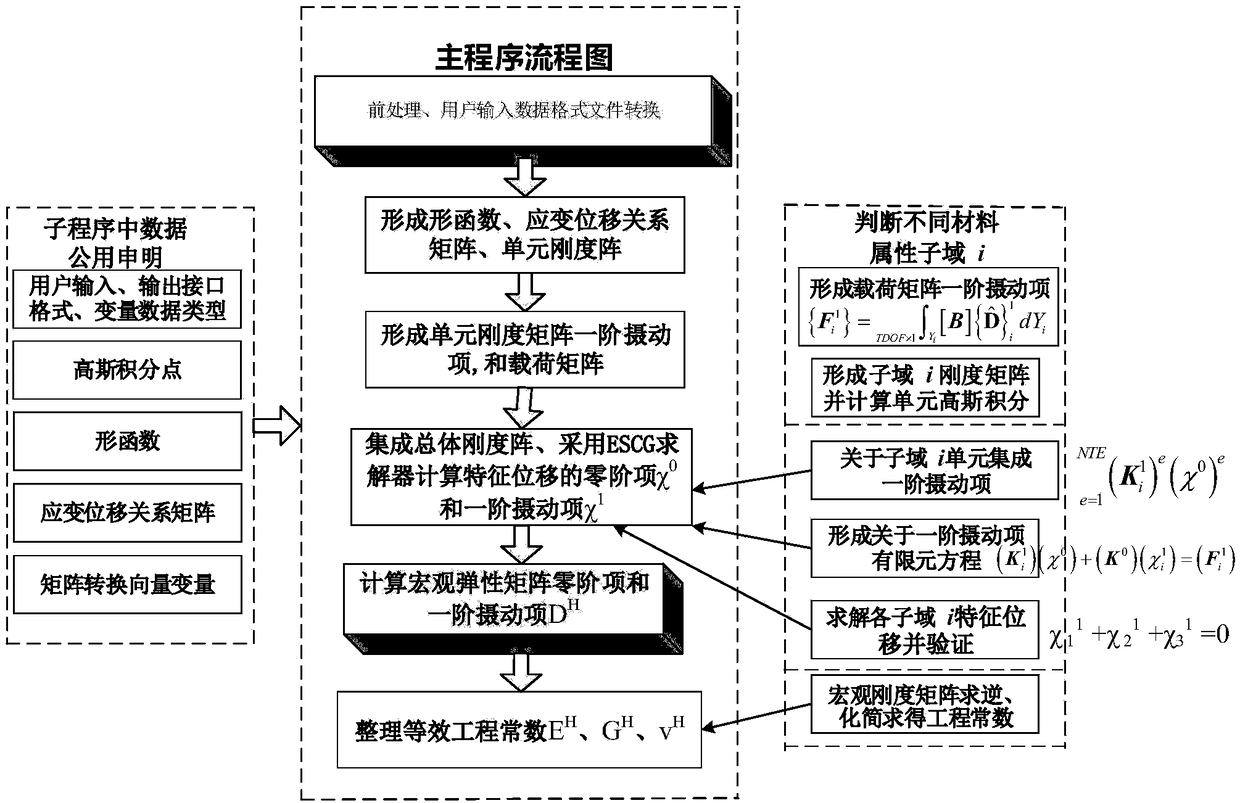
[0032] The present invention provides a statistical first-order perturbation expansion progressive homogenization method for predicting the elastic constitutive matrix of a randomly distributed composite material, comprising the following steps:
[0033] In the first step, determining the main source of the random variable includes two aspects: the physical properties of the geometric model and the material, and the present invention includes the Young's modulus, shear modulus, and Poisson's ratio of the n (n≥3) phase component material is described by a random normal distribution.
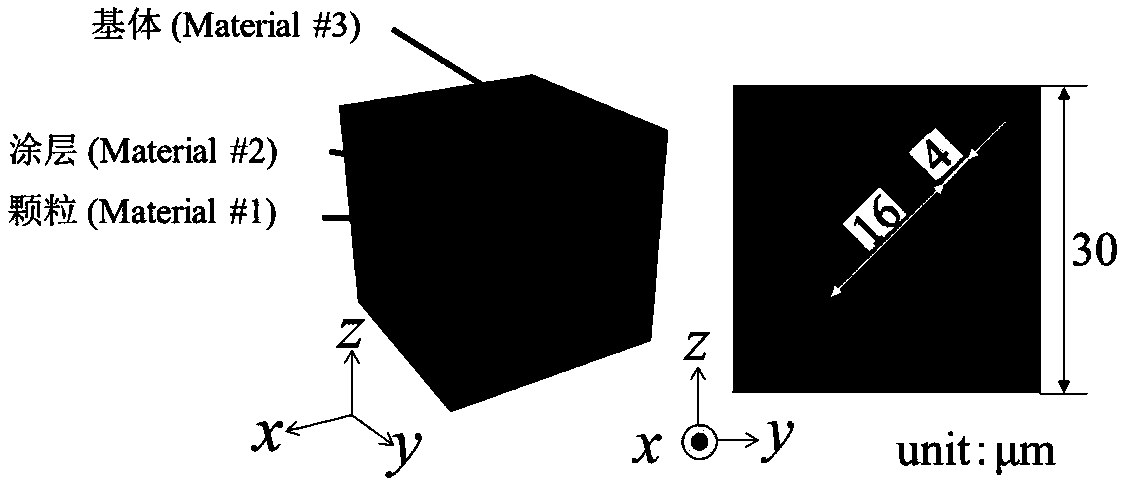
[0034] figure 2 Shown is a specific application example of the method of the present invention, in the three-phase composite material that coating, particle, matrix form, matrix material is macromolecule polymer, because manufacturing process is inaccurate, its Young's modulus assumption is positive State distribution N(16GPa,0.01 2 ), the particle material is gaseous substance N (400GPa, 0.01 ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com