Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Data clustering analysis method based on Grassmann manifold

An analysis method and data clustering technology, which is applied in the direction of instruments, character and pattern recognition, computer components, etc., can solve the problems that the clustering results are not accurate enough, and the Euclidean space cannot fully reflect the spatial distribution characteristics of data clustering, etc., to achieve The effect of improving accuracy

Inactive Publication Date: 2016-04-13
SHENYANG UNIV
View PDF0 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0002] In the standard spectral clustering analysis algorithm, the metric based on Euclidean space cannot fully reflect the complex spatial distribution characteristics of data clustering, resulting in inaccurate clustering results

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Data clustering analysis method based on Grassmann manifold
  • Data clustering analysis method based on Grassmann manifold
  • Data clustering analysis method based on Grassmann manifold

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

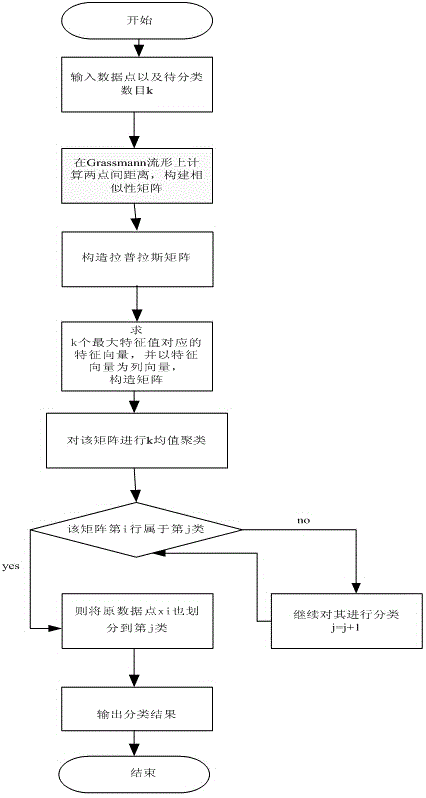
[0022] step 1:

[0023] Enter 200 data points of 100 dimensions , the number of clusters to be clustered is 2; (each data point is a 100-dimensional column vector, and 200 data points form a 100*200 matrix)

[0024] Step 2:

[0025] Based on the distance formula between two points on the Grassmann manifold, calculate the distance between data points and construct a similarity matrix .

[0026] Step 3:

[0027] Construct the Laplacian Matrix , where D is a diagonal matrix, .

[0028] Step 4:

[0029] Find the eigenvectors corresponding to the two largest eigenvalues ​​of the Laplacian matrix L, and construct the matrix ,in is a column vector.

[0030] Step 5:

[0031] Normalize the row vectors of V to get a matrix Y where .

[0032] Step 6:

[0033] Treat each row of Y as R 2 A point within the interval is classified using the K value algorithm.

[0034] Step 7:

[0035] If the th row belongs to class, the original data point also divided into Cl...

Embodiment 2

[0039] step 1:

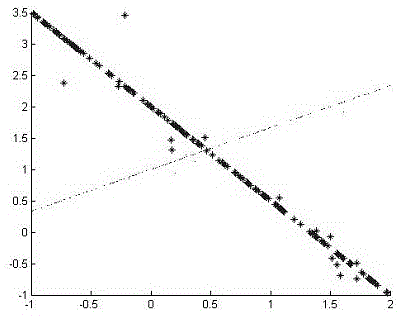
[0040] Input 340 2D data points , the number to be clustered is 2;

[0041] Step 2:

[0042] Based on the distance formula between two points on the Grassmann manifold, calculate the distance between data points and construct a similarity matrix .

[0043] Step 3:

[0044] Construct the Laplacian Matrix , where D is a diagonal matrix, .

[0045] Step 4:

[0046] Find the eigenvectors corresponding to the two largest eigenvalues ​​of the Laplacian matrix L, and construct the matrix ,in is a column vector.

[0047] Step 5:

[0048] Normalize the row vectors of V to obtain a matrix Y where .

[0049] Step 6:

[0050] Treat each row of Y as R 2 A point within the interval is classified using the K value algorithm.

[0051] Step 7:

[0052] If Y row belongs to class, the original data point also divided into Classification of output data points .

Embodiment 3

[0054] step 1:

[0055] Input 297 data points of 62 dimensions , the number to be clustered is 3;

[0056] Step 2:

[0057] Based on the distance formula between two points on the Grassmann manifold, calculate the distance between data points and construct a similarity matrix .

[0058] Step 3:

[0059] Construct the Laplacian Matrix , where D is a diagonal matrix, .

[0060] Step 4:

[0061] Find the eigenvectors corresponding to the two largest eigenvalues ​​of the Laplacian matrix L, and construct the matrix ,in is a column vector.

[0062] Step 5:

[0063] Normalizing the row vectors of V yields a matrix Y where .

[0064] Step 6:

[0065] Treat each row of Y as if it were R 2 A point in the space, using the K-means algorithm to classify it.

[0066] Step 7:

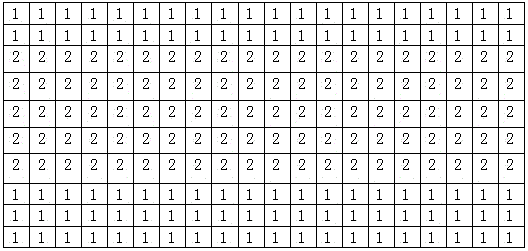
[0067] If the th row belongs to class, the original data point also divided into Classification of output data points . The classification results are as follows.

[0068]

[...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a data clustering analysis method based on Grassmann manifold, and relates to a spatial data clustering method. The method comprises the following processes of inputting N data points {x}<n><i=1> and the clustering number K to calculate the distance among the data points; constructing a Laplacian matrix L=D<-1 / 2>SD<-1 / 2>, wherein the D is the diagonal matrix, and D<ii>=[sigma]<J=1><n>S<ij>; calculating the feature vectors v<1>, v<2> to v<k> corresponding to the k maximum feature values of the Laplacian matrix L, and constructing a matrix V=[ v<1>, v<2> to v<k>] which is an element of a set R<nk>; and regarding each row of Y as a point in an R<k> space, and performing classification by using a K means algorithm. The data clustering analysis method based on Grassmann manifold has the advantages that the data distributed on different sub spaces can be effectively clustered; data sets with complicated geometrical structures can be analyzed; and the effective clustering is performed on the manifold space.

Description

technical field [0001] The invention relates to a spatial data clustering method, in particular to a data clustering analysis method based on a Grassmann manifold. Background technique [0002] In the standard spectral clustering analysis algorithm, the metric based on Euclidean space cannot fully reflect the complex spatial distribution characteristics of data clustering, resulting in inaccurate clustering results. The use of manifold space can more accurately describe the geometric relationship between data. Considering that the Grassmann manifold is a kind of entropy manifold in the Lie group manifold, it not only has a smooth surface space expression, but also has the characteristics that are more suitable for measuring the distance between data points, which can make the clustering results more accurate, so this application A data clustering analysis method based on Grassmann manifold is proposed. Contents of the invention [0003] The purpose of the present inventi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06K9/62
CPCG06F18/23
Inventor 谢英红韩晓微涂斌斌
Owner SHENYANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com