Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

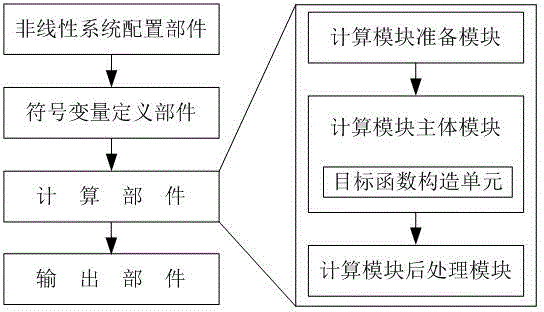
Harmonic balance method device of single-degree-of-freedom system

A technology of harmonic balance and degrees of freedom, which is applied in the field of harmonic balance method devices of single-degree-of-freedom systems, can solve the problems of complex implementation, less number of analyzed harmonic terms, time-consuming and low precision, etc.

Active Publication Date: 2015-09-02
HENAN POLYTECHNIC UNIV
View PDF2 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] Aiming at the problems of complex analysis of nonlinear systems by harmonic balance method, few analysis harmonic items, time-consuming and low precision, the purpose of the present invention is to provide a single-degree-of-freedom nonlinear system harmonic balance method device to solve above question

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Harmonic balance method device of single-degree-of-freedom system
  • Harmonic balance method device of single-degree-of-freedom system
  • Harmonic balance method device of single-degree-of-freedom system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0167] Example 1: The equation of a single degree of freedom nonlinear system is

[0168] .

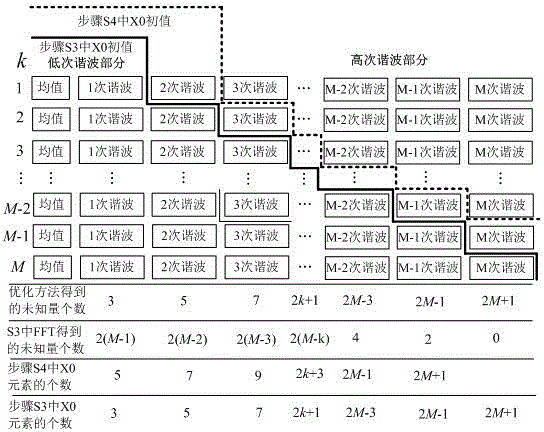
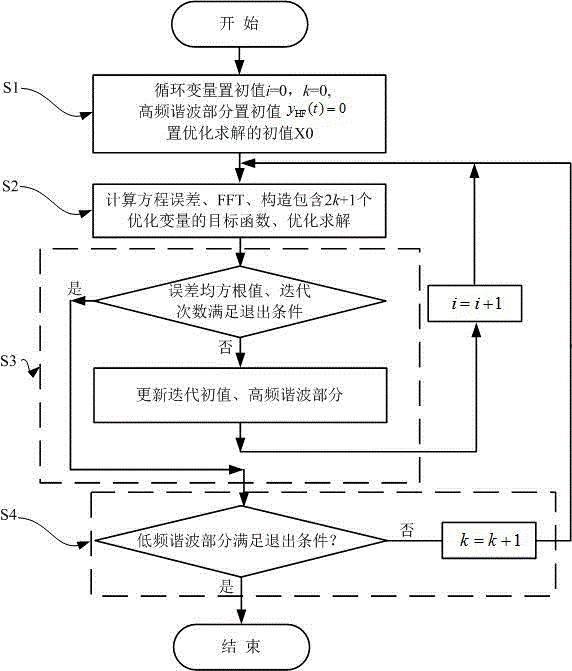
[0169] Assuming that the angular frequency of the first harmonic in the response is 1, set the initial iteration value x0=[0,0,0], and only consider the harmonics below the 32nd order, that is M =32, the maximum number of inner loops is 5, the number of sampling points N =64, the error limit in step S4 is set to , The range of random disturbance is . Implement technical solution 3. along with k As the value increases, the root mean square error of the equation decreases rapidly. The mean square error of the equation in the first 6 cycles is as follows:

[0170] 5.656854249492381e+000, 2.496859179098087e-003, 8.156122475628342e-008,

[0171] 4.360844843951736e-012, 4.360844843951736e-012, 4.360844843951736e-012.

[0172] The amplitude and phase of each harmonic are as Figure 5 As shown, the 0th harmonic corresponds to the average value, the 1st to 6th harmonics are obtained by the nonlinea...

Embodiment 2

[0174] Example 2: Modify the incentive in Example 1 to cos2 t , Assuming that the angular frequency of the first harmonic in the response is 2, set the initial iteration value x0 to be randomly generated, and other parameters are the same as in embodiment 1. Implement technical solution 3. The amplitude and phase of each harmonic are as Image 6 As shown, the 0th harmonic corresponds to the average value, the 1st to 6th harmonics are obtained by the nonlinear optimization in step S2, and the 7th to 32nd harmonics are obtained by the numerical FFT in step S3. when k > After 2, the iteration result tends to be constant, and the accuracy level is .

Embodiment 3

[0175] Example 3: Modify the incentive in Example 1 to cos3 t , Assuming that the angular frequency of the first harmonic in the response is 3, set the initial iteration value x0 to be randomly generated, and only consider the harmonics below the 32th order, that is M =32, the maximum number of inner loops is 4, the number of sampling points N =64,. Implement technical solution 3. along with k As the value increases, the root-mean-square error of the equation decreases rapidly, such as Figure 7 As shown, the accuracy level of the iteration result is . The amplitude and phase of each harmonic are as Figure 8 As shown, the 0th harmonic corresponds to the average value, the 1st to 6th harmonics are obtained by the nonlinear optimization in step S2, and the 7th to 32nd harmonics are obtained by the numerical FFT in step S3.

[0176] The device provided by the invention only needs to be changed M The value of can control the number of harmonics, which is convenient for application...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a harmonic balance method device of a single-degree-of-freedom system and belongs to the field of computer engineering application. The device comprises a nonlinear system configuration part, a symbolic variable definition part, a computation part and an output part, wherein an objective function construction unit is arranged in the computation part and is used for dynamically constructing an objective function needed for optimizing and solving mean values, amplitudes of each harmonic and phases. A harmonic balance method adopted by the device only considers limited harmonic in response and divides the harmonic into a low-frequency harmonic portion and a high-frequency harmonic portion. Starting from that the low-frequency portion only includes mean values and first harmonic, the solving accuracy is improved through optimization and iteration, times of the highest harmonic contained by the low-frequency portion are continuously increased, the lowest harmonic of the high-frequency harmonic portion is reduced at the same time, the result obtained through computation by using the low-frequency harmonic portion is used as an initial value, and finally the mean values in response, the amplitudes of the limited harmonic and the phase are solved. The device provided by the invention has the advantages of very fast convergence speed and very high accuracy.

Description

technical field [0001] The invention belongs to the field of computer engineering applications, and in particular relates to a single-degree-of-freedom system harmonic balance method device. Background technique [0002] Harmonic balance method is a very effective method to deal with nonlinear system problems. Many practical control systems meet the conditions for applying this method, so they have been widely used in the field of engineering technology, such as gear transmission, vibrating conveyor, vibrating cooler, vibrating mill, engine, automobile steering, electronic circuits, etc. Analysis and design of machines and systems. Among them, the single-degree-of-freedom nonlinear system is the most common, and it is also the basis for the research and application of the multi-degree-of-freedom nonlinear system. The basis of its application and the processing method it adopts are: express the output / response in the form of Fourier series, only consider the finite harmonic...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/14
Inventor 陈国强王耿康件丽
Owner HENAN POLYTECHNIC UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com