Deriving effective corners for complex correlations
a complex correlation and effective corner technology, applied in the field of semiconductor design, can solve the problems of extreme leakage, difficult or nearly impossible control of line-width cd-variation, and considerable challenge in achieving reasonable yield in light of manufacturing variability
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Benefits of technology
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
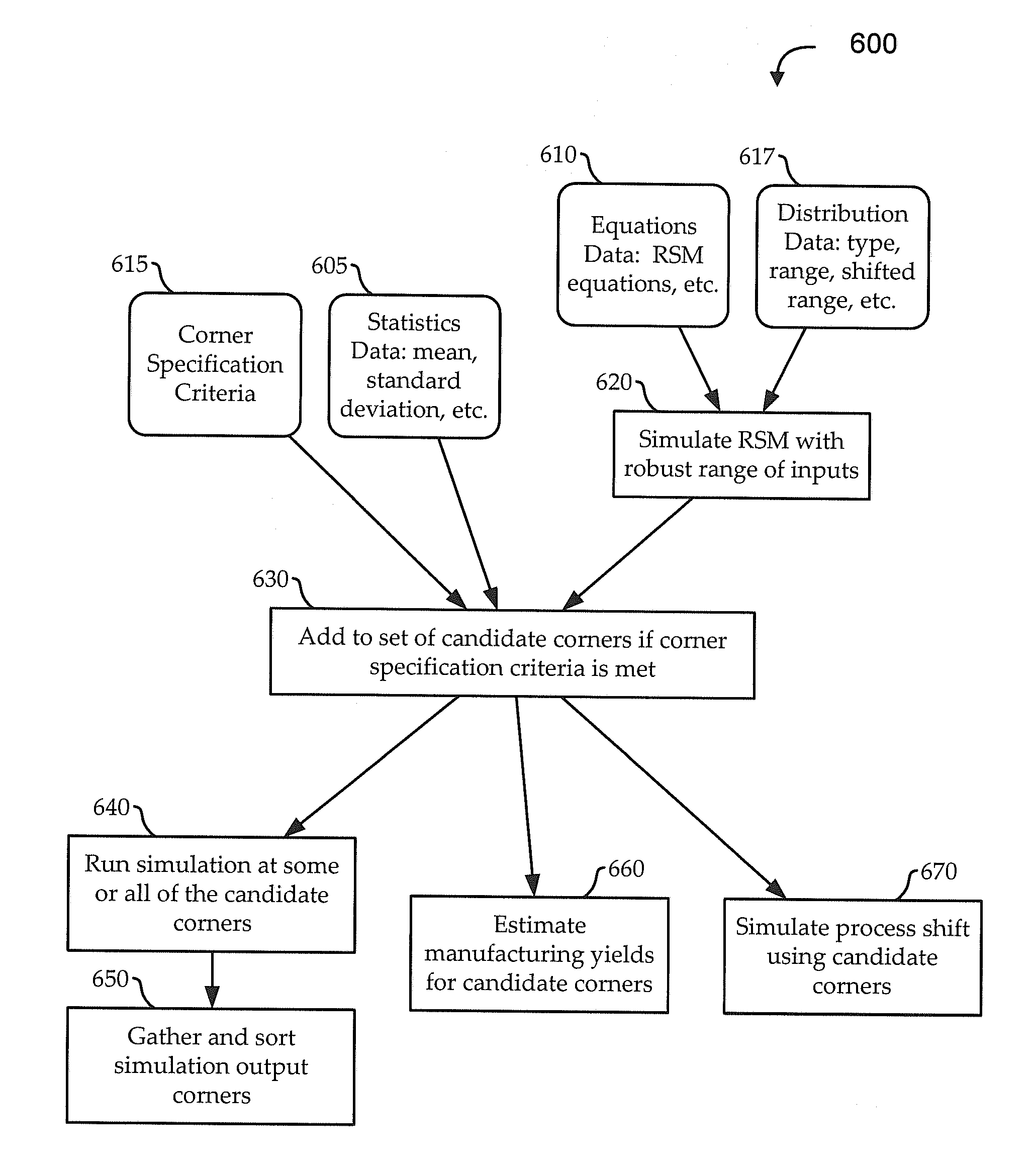
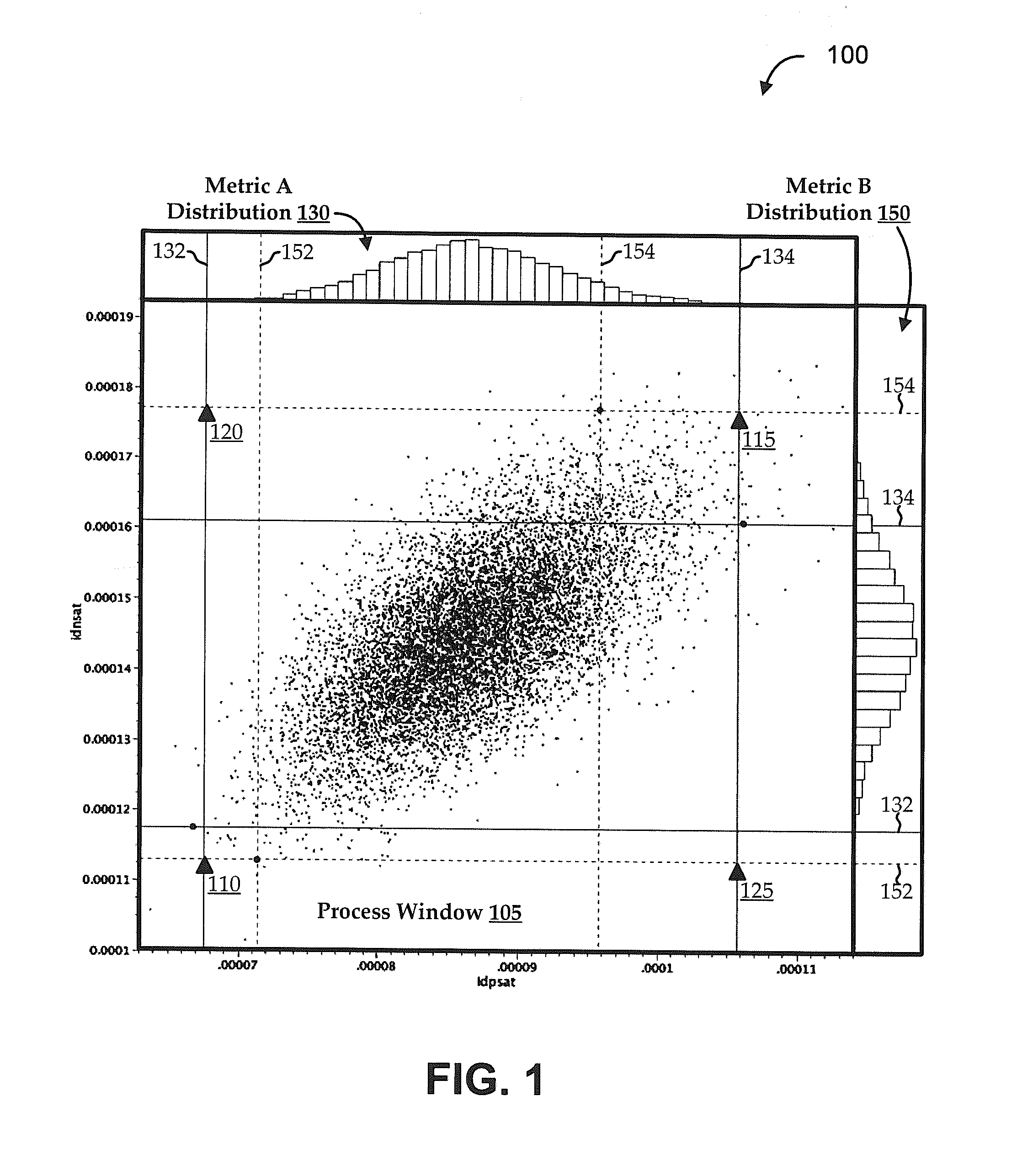
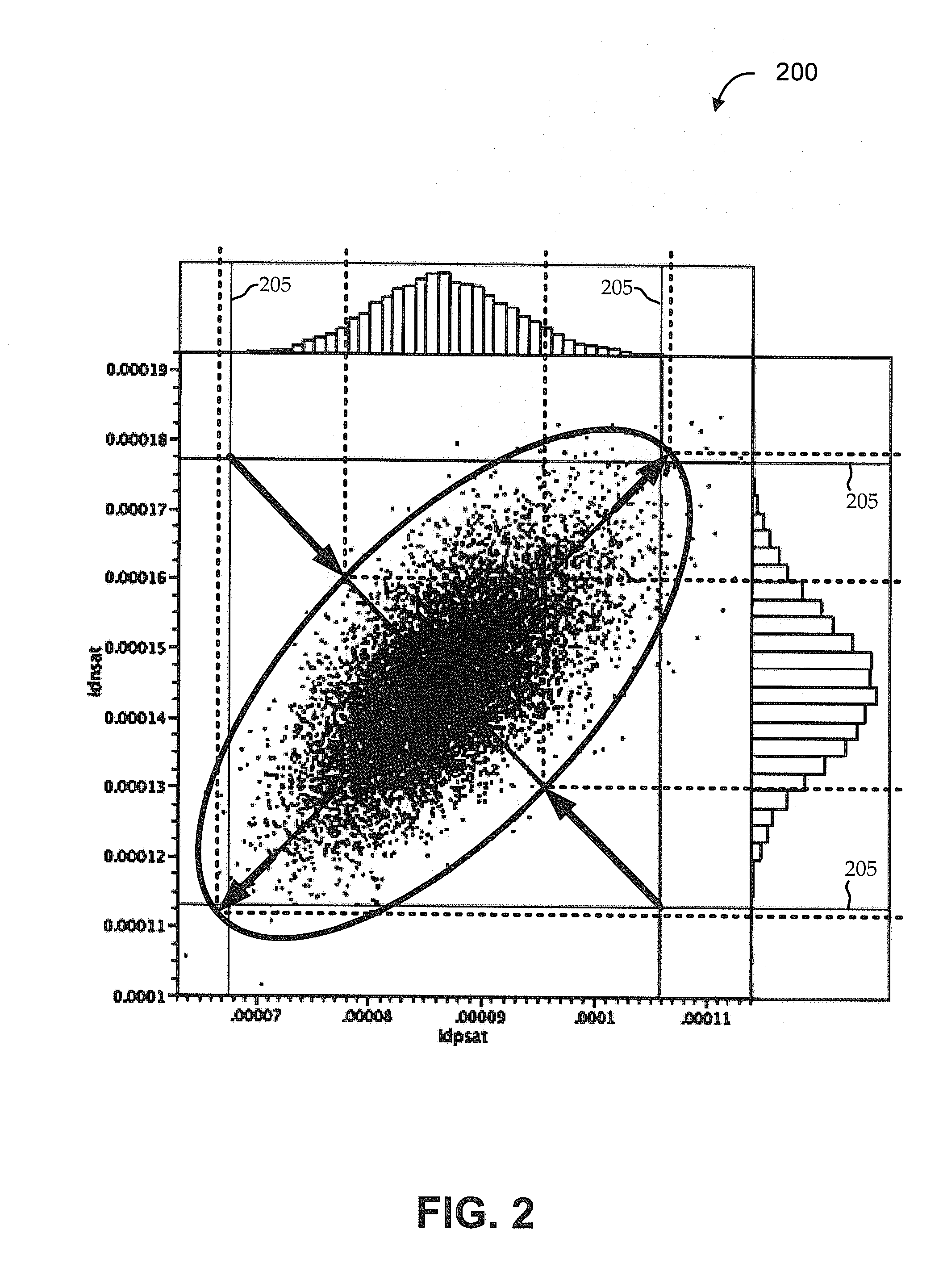
[0016]It has become increasingly common for circuit design efforts to include process design. For example, newer circuit designs often push the limits of available process technologies. Even when existing manufacturing processes are used, the tolerances, complexities, and other features of those processes can impact design of the circuits being manufactured using those processes. Variations in these process parameters, circuit metrics, and / or other factors (generally referred to herein as “metrics”) can each impact yield. Accordingly, achieving a desired effective yield for a full circuit product (e.g., a microprocessor having a number of sub-circuits) can involve modeling, analyzing, and designing in a manner that simultaneously accounts for multiple of those metrics.
[0017]For example, during the design of semiconductor devices (e.g., single transistors, circuits, chips, wafers, etc.), circuit simulations, like post-layout circuit simulations, may be performed using a net-list extr...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com