Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

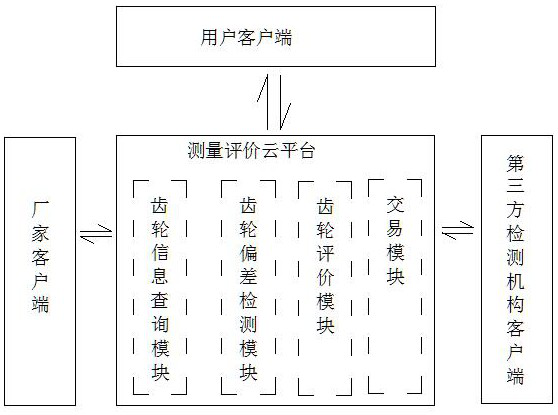
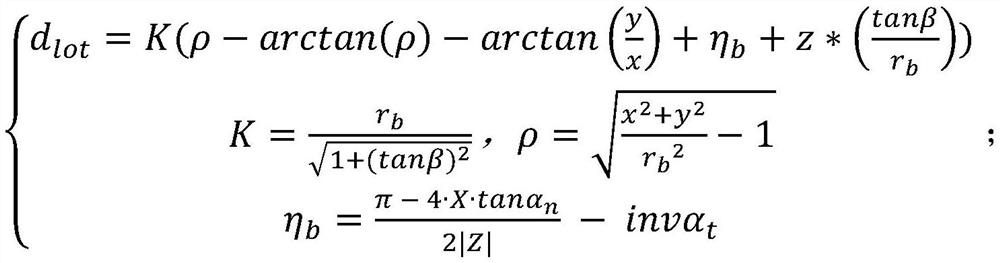Gear digital measurement and evaluation cloud system and measurement and evaluation method

A gear measurement and cloud system technology, applied in manufacturing computing systems, electrical digital data processing, digital data information retrieval, etc., can solve problems such as gear manufacturing impact, untimely transmission, and untimely process feedback.

Active Publication Date: 2021-10-12
HENAN POLYTECHNIC UNIV
View PDF3 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] Due to the different gear detection platforms and detection methods of major manufacturers, the programming language, data interface, and format used are inconsistent, which will cause a series of problems such as the inability to unify the format and content of the gear measurement data, and the transmission is not timely. Manufacturing has had a big impact
[0005] On the other hand, in the existing gear trading process, there are problems of low communication efficiency and untimely process feedback

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Gear digital measurement and evaluation cloud system and measurement and evaluation method
  • Gear digital measurement and evaluation cloud system and measurement and evaluation method
  • Gear digital measurement and evaluation cloud system and measurement and evaluation method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0137] When using the two-dimensional Chebyshev polynomial alone as the basis function to calculate the deviation surface equation of the gear to be measured, assuming that there are s tooth surface deviation point data in the tooth surface deviation point cloud data, using the least square method to solve the deviation surface equation is equivalent to The deviation surface equation is calibrated s times, that is, the best approximate surface after s calibrated is obtained.

[0138] The following formula is a system of equations established by the method of least squares, and the deviation surface equation d is solved by this system of equations C :

[0139]

[0140] The deviation surface equation defined in the u′-v′-d tooth surface coordinate system is calculated by the two-dimensional Chebyshev polynomial as:

[0141] d C =A C0 *1+A C1 *u′+A c2 *v′+A C3 *(2u′ 2 -1)+A C4 *u′v′+A C5 *(2v′ 2 -1);

[0142] The specific proportional relationship between the deviatio...

Embodiment 2

[0144] When the two-dimensional Legendre polynomial is used alone as the basis function to calculate the deviation surface equation of the gear to be measured, assuming that there are s tooth surface deviation point data in the tooth surface deviation point cloud data, the least square method is used to solve the deviation surface equation. The deviation surface equation is calibrated s times, that is, the best approximate surface after s calibrated is obtained.

[0145] The following formula is a system of equations established by the method of least squares, and the deviation surface equation d is solved by this system of equations L :

[0146]

[0147] Find d through the two-dimensional Legendre polynomial L The equation of the deviation surface defined in the u′-v′-d tooth surface coordinate system is:

[0148]

[0149] The specific proportional relationship between the deviation item and the coefficient is: the tooth pitch deviation is equal to A L0 , the tooth p...

Embodiment 3

[0151] The two-dimensional Legendre polynomial and the two-dimensional Chebyshev polynomial are respectively used as the basis functions to obtain the corresponding deviation surface equations, and then according to the evaluation requirements for different types of tooth surface deviations, the coefficients of the corresponding deviation surface equations are selected to obtain more accurate Different types of tooth surface deviation evaluation results.

[0152] Assuming that there are s tooth surface deviation point data in the tooth surface deviation point cloud data, when the least square method is used to solve the deviation surface equation, it is equivalent to correcting the deviation surface equation s times, that is, the best approximate surface after s corrections is obtained .

[0153] The deviation surface equations obtained by using two-dimensional Chebyshev polynomials as basis functions are:

[0154] d C =A C0 *1+A C1 *u′+A C2 *v′+A C3 *(2u′ 2 -1)+A C4 *...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a gear digital measurement and evaluation cloud system and a measurement and evaluation method. The system comprises a user client and a measurement and evaluation cloud platform. The user client is used for providing gear information query, gear deviation detection and gear detection result display for a user; the measurement and evaluation cloud platform comprises a gear information query module, a gear deviation detection module and a gear evaluation module; the gear information query module is used for establishing a gear information base and performing query and feedback; the gear deviation detection module is used for carrying out gear deviation calculation; the gear evaluation module is used for evaluating whether the gear to be measured is qualified or unqualified, and taking the visual image, the deviation data and the evaluation result as a gear detection result, and feeding back the gear detection result to a user client. According to the invention, the efficiency of gear measurement data cloud digital exchange and measurement resource sharing can be improved, online measurement and evaluation of the gear can be realized, real data of the gear can be obtained, and data support is provided for a gear producer and a gear purchaser.

Description

technical field [0001] The invention relates to the field of gear measurement and evaluation, in particular to a gear digital measurement and evaluation cloud system and a measurement and evaluation method. Background technique [0002] As the most important basic component of the high-end assembly manufacturing industry, gears are widely used in aerospace, wind power equipment manufacturing, shipbuilding, equipment manufacturing, and automobile industries. As the gears produced are changing from low-end to high-end, the requirements for gear devices, gear measurement methods and technical requirements for gear manufacturing are constantly increasing. The provision of gear measurement data facilitates the adjustment of gear processing parameters and the traceability of errors, laying a foundation for the improvement of gear manufacturing accuracy. [0003] With the continuous development of the Internet and information technology, the era of big data has come. In March 200...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06Q10/06G06Q50/04G06F16/583G06F16/58G06T7/60G06T7/62
CPCG06Q10/06395G06Q50/04G06F16/583G06F16/5866G06T7/60G06T7/62G06T2207/10028G06T2207/30164Y02P90/30
Inventor 张登攀岳佳佳李键闫勇刚郑义博
Owner HENAN POLYTECHNIC UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com