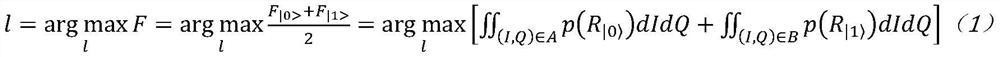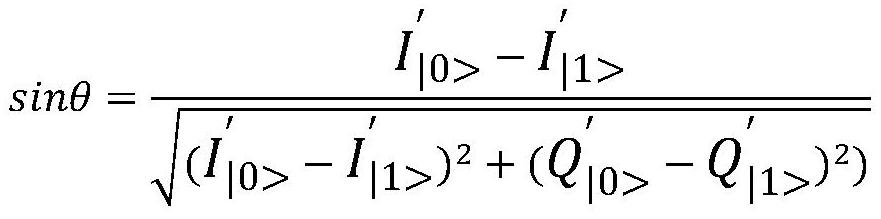Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Acquisition method of threshold line for confirming quantum bit quantum state

A technology of qubits and acquisition methods, applied in image data processing, instruments, character and pattern recognition, etc., can solve problems such as errors and affecting the reading results of unknown quantum states

Active Publication Date: 2020-10-30
ORIGIN QUANTUM COMPUTING TECH (HEFEI) CO LTD
View PDF6 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The problem with the prior art is that, ideally, the setting of the perpendicular line connecting the center points of the two distribution graphs as the threshold dividing line can meet the requirements most of the time, but due to factors such as the preparation error of the quantum state, it will lead to There are errors in this threshold line that may affect the reading results of unknown quantum states

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Acquisition method of threshold line for confirming quantum bit quantum state
  • Acquisition method of threshold line for confirming quantum bit quantum state
  • Acquisition method of threshold line for confirming quantum bit quantum state

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0063] Specifically, combined with figure 1 , Embodiment 1 of a method for obtaining a threshold line for confirming the qubit quantum state of the present invention comprises the following steps:

[0064] Step 10. Prepare the qubits into the first quantum state and perform repeated measurements to obtain the coordinate point data of the reading signals of multiple qubits on the orthogonal plane coordinate system, which is recorded as the first set R |0> ; The qubit is prepared into a second quantum state and it is repeatedly measured to obtain the coordinate point data of a plurality of qubit read signals on the orthogonal plane coordinate system, which is denoted as the second set R |1> , wherein: the first quantum state and the second quantum state are known quantum states and are different from each other, wherein: the orthogonal plane coordinate system is set to an I-Q coordinate system;

[0065] Specifically, the first quantum state can be selected from the |0> state qu...

Embodiment 2

[0081] It should be noted that, under the premise of satisfying the above two-dimensional double-Gaussian distribution statistical model, the obtained current threshold line can be mathematically proved that the current threshold line and the first statistical center point coordinates (I |0> , Q |0> ) and the second statistical central point coordinates (I |1> , Q |1> )vertical.

[0082] The proof process is as follows:

[0083] A known:

[0084]

[0085]

[0086]

[0087] It may be assumed that the expression of the finally obtained optimal threshold line in the IQ coordinate system is:

[0088] aI+bQ+c=0, where ab≠0, b≥0, a 2 +b 2 = 1

[0089] Obtain the angle φ between the optimal threshold line and the I axis, and rotate all the coordinate point data in the first set and the second set clockwise with the coordinate origin as the center in the IQ coordinate system, wherein the updated Coordinates of the first statistical center point (I |0> , Q |0> ) and ...

Embodiment 3

[0133] It should be noted that when the qubit is in the |0> state or the |1> state, the data after the analysis of the qubit reading signal is repeatedly obtained. Due to different statistical data, the first statistical central point of the two-dimensional double Gaussian distribution graph Coordinates (I |0> , Q |0> ) and the second statistical center point coordinates (I |1> , Q |1> ) will float and change, but the distance between the two center coordinates, that is remains unchanged; secondly, the noise level of the system does not change much, and can still be approximated as σ 1 and σ 2 . Finally, the distribution of qubit reading results on the i-q coordinate system at this time still obeys the two-dimensional double Gaussian statistical distribution. On the premise that the above three conditions are established, we can still adopt the same rotation transformation method as in Example 2 to transform the theoretical threshold straight line into a single variable...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an acquisition method of a threshold line for confirming a quantum bit quantum state, and relates to the field of quantum measurement and control. The acquisition method includes the steps: preparing the quantum bits into a first quantum state and a second quantum state, and repeatedly measuring the first quantum state and the second quantum state respectively to obtain coordinate point data of a plurality of quantum bit reading signals on an orthogonal plane coordinate system; respectively marking as a first set and a second set, respectively carrying out Gaussian fitting on the coordinate points of the first set and the second set to obtain a first statistical center coordinate point and a second statistical center coordinate point of the Gaussian fitting graph respectively corresponding to the first set and the second set, and respectively corresponding to a first standard deviation and a second standard deviation; respectively determining a first probabilitydensity distribution function in the first set and a second probability density distribution function in the second set; and determining a fidelity function, and determining a corresponding thresholdline as an optimal threshold line when the fidelity function takes the maximum value. The threshold line established according to the acquisition method provided by the invention can provide more accurate reference for the judgment of unknown quantum states.

Description

technical field [0001] The invention belongs to the field of quantum measurement and control, in particular to a method for obtaining a threshold line for confirming the quantum state of a qubit. Background technique [0002] Qubit information refers to the quantum state described by the qubit. The basic quantum states are |0> state and |1> state. After the qubit is operated, the quantum state of the qubit changes. On the quantum chip, it is reflected as After the quantum chip is executed, the quantum state described by the qubit is the execution result of the quantum chip, which is carried and transmitted by the qubit read signal. [0003] Quickly analyze the quantum state of the qubit by reading the signal of the qubit. The analysis of the quantum state of the qubit is the key work to understand the performance of the quantum chip. In the previously applied patent, a method for determining the quantum state of the qubit is provided, which includes the following steps...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06K9/62G06T7/10G06T7/136
CPCG06T7/136G06T7/10G06N10/70G06V10/763
Inventor 孔伟成
Owner ORIGIN QUANTUM COMPUTING TECH (HEFEI) CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com