Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Joint Estimation Method of Sensor Amplitude and Phase Error and Target Arrival Angle

An amplitude and phase error and joint estimation technology, which is applied in the field of joint estimation of sensor amplitude and phase error and target arrival angle, can solve the problems of limited estimation accuracy, increase the computational complexity of the algorithm, do not consider sensor errors, etc., and achieve high estimation accuracy and high accuracy. The effect of low computational complexity and high estimation accuracy

Active Publication Date: 2022-07-15
HARBIN ENG UNIV
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The current solution to this kind of problem is to finely subdivide the spatial grid. The disadvantages are: firstly, the target cannot be guaranteed to be on the discrete grid, and the improvement of estimation accuracy is very limited; Greatly improve the computational complexity of the algorithm
If the amplitude and phase errors that may exist in the sensor are considered in practical applications, the existing algorithms cannot obtain accurate angle estimates
[0004] Traditional DoA estimation is based on an ideal situation, that is, it does not consider the possible errors of the sensor in practical applications, resulting in limitations in its performance

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Joint Estimation Method of Sensor Amplitude and Phase Error and Target Arrival Angle
  • Joint Estimation Method of Sensor Amplitude and Phase Error and Target Arrival Angle
  • Joint Estimation Method of Sensor Amplitude and Phase Error and Target Arrival Angle

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

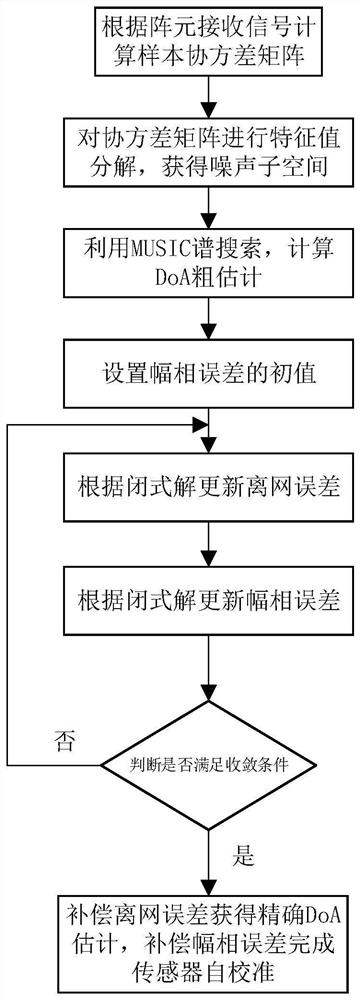
[0056] Embodiment 1: A joint estimation method of sensor amplitude and phase error and target arrival angle in a partial calibration array of the present invention includes the following steps:

[0057] (1) M uniformly arranged omnidirectional receiving antennas form an array, and the spacing d of the array elements is half of the wavelength λ, assuming that the first antenna is used as a reference array element.

[0058] (2) Calculate the sample covariance matrix of the received signal within T snapshots, obtain the noise subspace by decomposing the eigenvalues ​​of the covariance matrix, and then obtain a rough estimate of DoA according to the MUSIC spectrum search method.

[0059] (3) A signal model with both amplitude and phase errors and off-grid errors is established, and a multivariate optimization problem is constructed according to the orthogonality of the signal subspace and the noise subspace.

[0060] (4) The original problem is solved by the method of alternating ...

Embodiment 2

[0097] The estimation of the target arrival angle and the sensor amplitude and phase error of the present invention mainly includes the following steps:

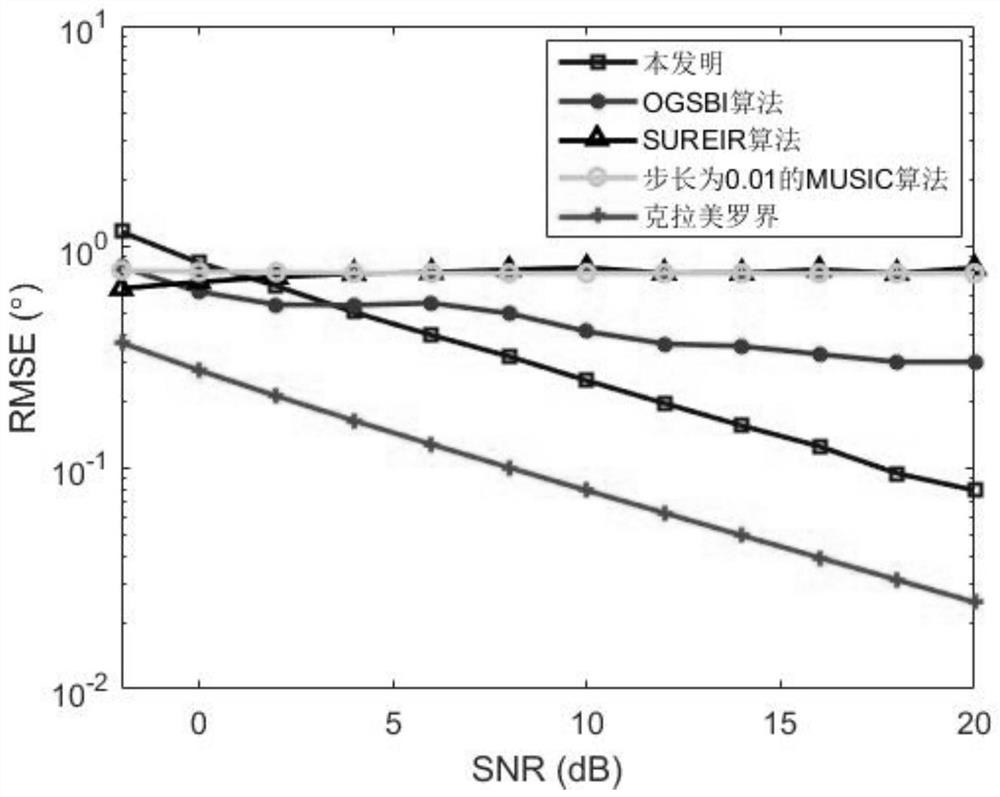
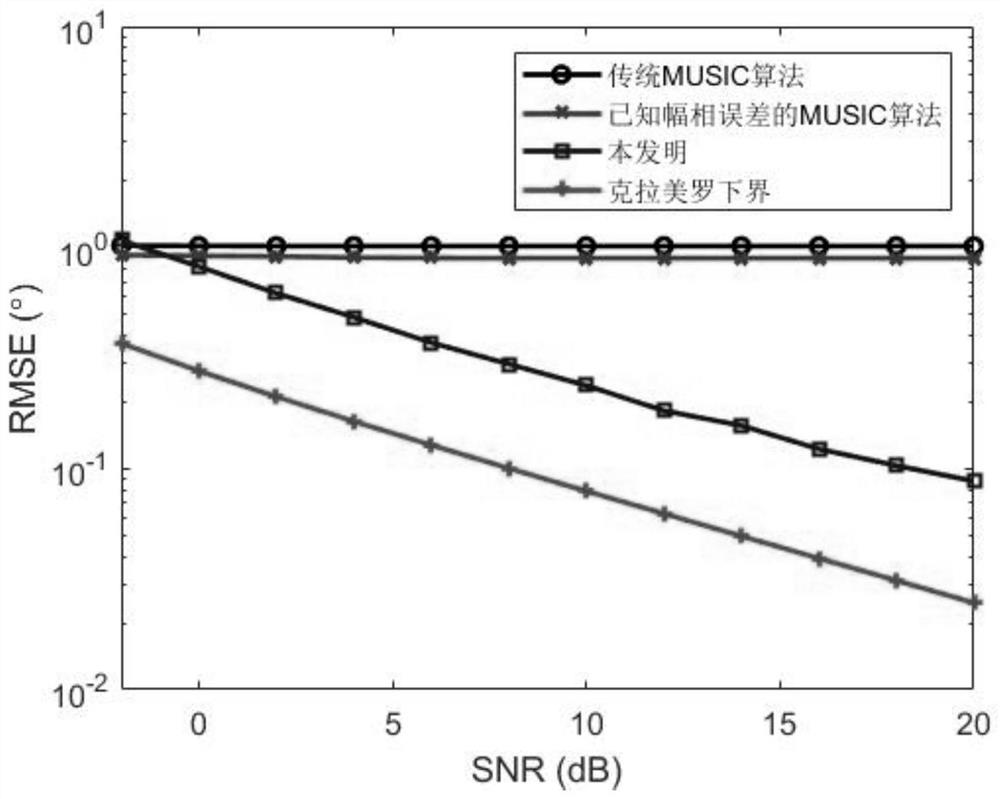
[0098] Step 1: Use the sensor to receive the signal data within T snapshot times, and calculate the corresponding covariance matrix:

[0099]

[0100] where y(t) represents the received signal vector of the array captured by the t-th snapshot.

[0101] Step 2: Perform eigenvalue decomposition on the obtained covariance matrix to obtain the signal subspace And use the orthogonality of the signal subspace and the noise subspace to construct the MUSIC spectral function:

[0102]

[0103] in the formula is the steering vector of the array, and θ is the spatial angle. By dividing the discrete grid θ over the entire space [-90°, 90°] l ∈[θ 1 ,θ 2 ,…,θ L ], search for the K peaks in equation (13) to obtain a rough estimate of the K target angles

[0104] Step 3: Calculate the off-grid error of the k-th target by t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a joint estimation method of sensor amplitude and phase error and target arrival angle. Firstly, the relationship between steering vector and DoA rough estimation and off-grid error is established according to the first-order Taylor expansion, and the noise subspace in the multiple signal classification algorithm is used. Orthogonality with the signal subspace, a multi-variable optimization problem whose parameters are amplitude-phase error and off-grid error are constructed. Through the alternate iteration of closed-form solutions of the sub-problems, the error compensation of the sensor and the accurate estimation of DoA are finally realized. While realizing sensor self-calibration, the invention has the advantages of super-resolution angle estimation of MUSIC algorithm, and simultaneously solves the off-grid problem existing in the spectrum search process, which can greatly improve the accuracy and robustness of DoA estimation in practical applications. .

Description

technical field [0001] The invention relates to a joint estimation method of sensor amplitude and phase error and target arrival angle, and belongs to the technical field of array signal processing. Background technique [0002] The estimation of the target angle of arrival based on the antenna array is widely used in many fields such as radar, sonar, wireless communication and imaging. The working state of the sensors in the array directly affects the accuracy of angle estimation. In practical applications, the antenna array will always be affected by uncertain factors and generate errors, such as argument and phase errors, mutual coupling between antennas, and antenna position errors, etc., which directly lead to the performance of traditional angle estimation algorithms. fall or even fail. In modern array signal processing technology, scholars have established a partially calibrated array model, which aims to jointly estimate the angle of arrival and the sensor's amplit...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/20G06F111/06
Inventor 王伟董福王黄平魏震宇黄智开
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com