Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for solving fracture problem of functionally graded piezoelectric material with any attribute

A piezoelectric material and functional gradient technology, applied in the field of fracture mechanics, can solve the problems of inaccurate crack parameters, limitations, and failure to consider any properties of functional gradient piezoelectric materials, etc., and achieve a wide range of applications.

Pending Publication Date: 2020-01-17
HARBIN UNIV OF SCI & TECH
View PDF8 Cites 6 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to solve the fracture problem of the existing functionally graded piezoelectric material without considering the arbitrary properties of the functionally graded piezoelectric material, resulting in inaccurate crack parameters and limiting the solution of the fracture problem of the existing functionally graded piezoelectric material problem of the application of the solution method, and proposes a method for solving the fracture problem of functionally graded piezoelectric materials with arbitrary properties

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for solving fracture problem of functionally graded piezoelectric material with any attribute
  • Method for solving fracture problem of functionally graded piezoelectric material with any attribute
  • Method for solving fracture problem of functionally graded piezoelectric material with any attribute

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

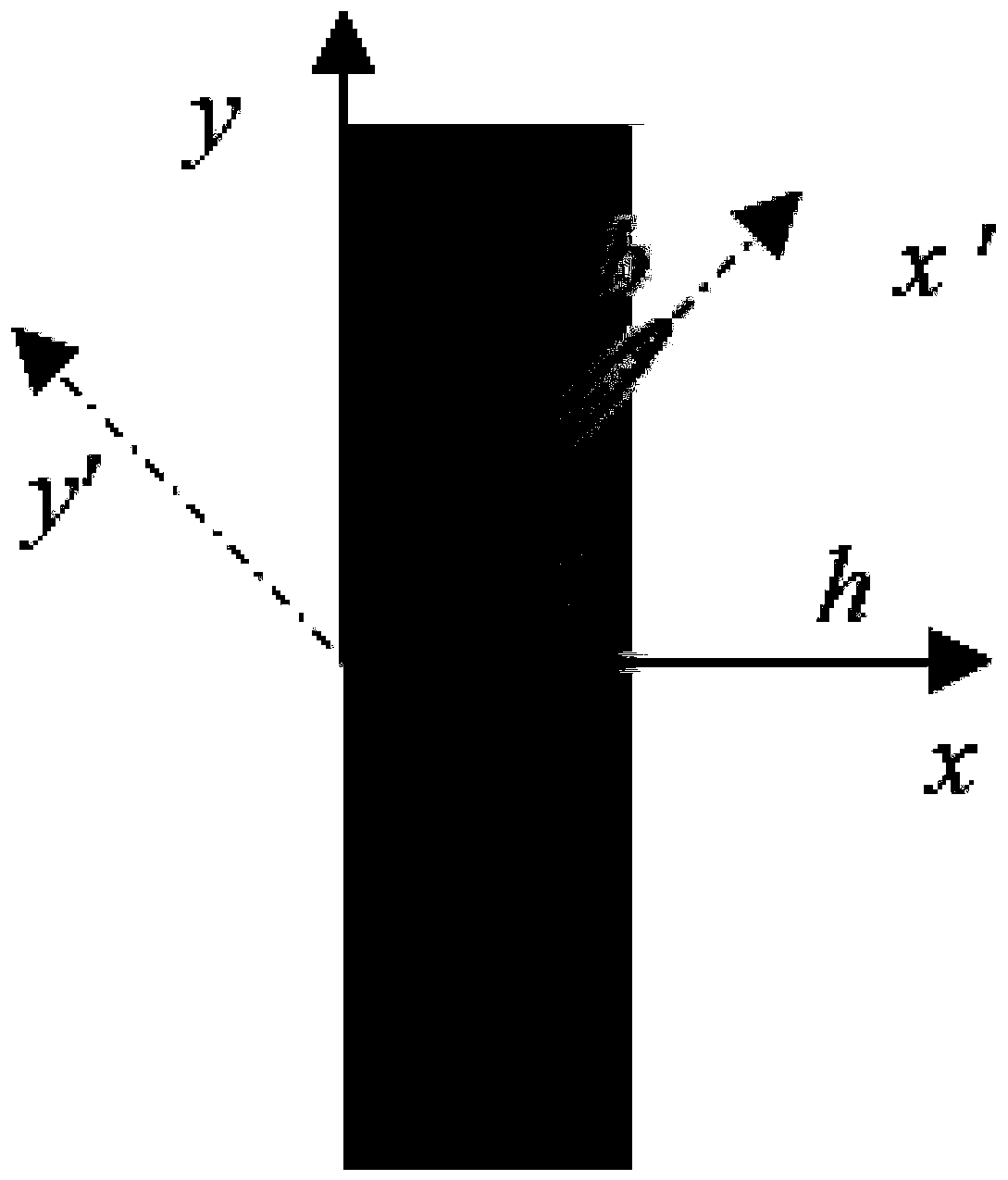
[0017] Specific implementation mode one: as figure 1 As shown, a method for solving the fracture problem of a functionally graded piezoelectric material with arbitrary properties described in this embodiment, the method includes the following steps:

[0018] Step 1, establishing the constitutive equation and equilibrium equation of the functionally graded piezoelectric material;

[0019] Step two, such as figure 2 As shown, in order to solve the fracture problem of functionally graded piezoelectric materials with arbitrary properties, for the arbitrariness of the properties of functionally graded piezoelectric materials:

[0020] The functionally graded piezoelectric material is uniformly divided into several layers along the thickness direction, assuming that the material properties of each layer change with the form of exponential function, and the material properties of adjacent layers are continuous at the interface, the constitutive equation and equilibrium established ...

specific Embodiment approach 2

[0026] Specific implementation mode two: the difference between this implementation mode and specific implementation mode one is: the specific process of the step one is:

[0027] For a functionally graded piezoelectric material with a thickness h, the constitutive equation of the functionally graded piezoelectric material is established as:

[0028]

[0029] Where: τ xz Represents the shear stress in the z-axis direction of the functionally graded piezoelectric material on a plane perpendicular to the x-axis, τ yz Represents the z-axis shear stress of the functionally graded piezoelectric material on a plane perpendicular to the y-axis, D x Represents the electrical displacement of the functionally graded piezoelectric material in the x-axis direction, D y Represents the electrical displacement of the functionally graded piezoelectric material in the y-axis direction; the x-axis, y-axis, and z-axis are the three axes of the space Cartesian coordinate system;

[0030] w ...

specific Embodiment approach 3

[0039] Specific implementation mode three: the difference between this implementation mode and specific implementation mode two is: the specific process of said step two is:

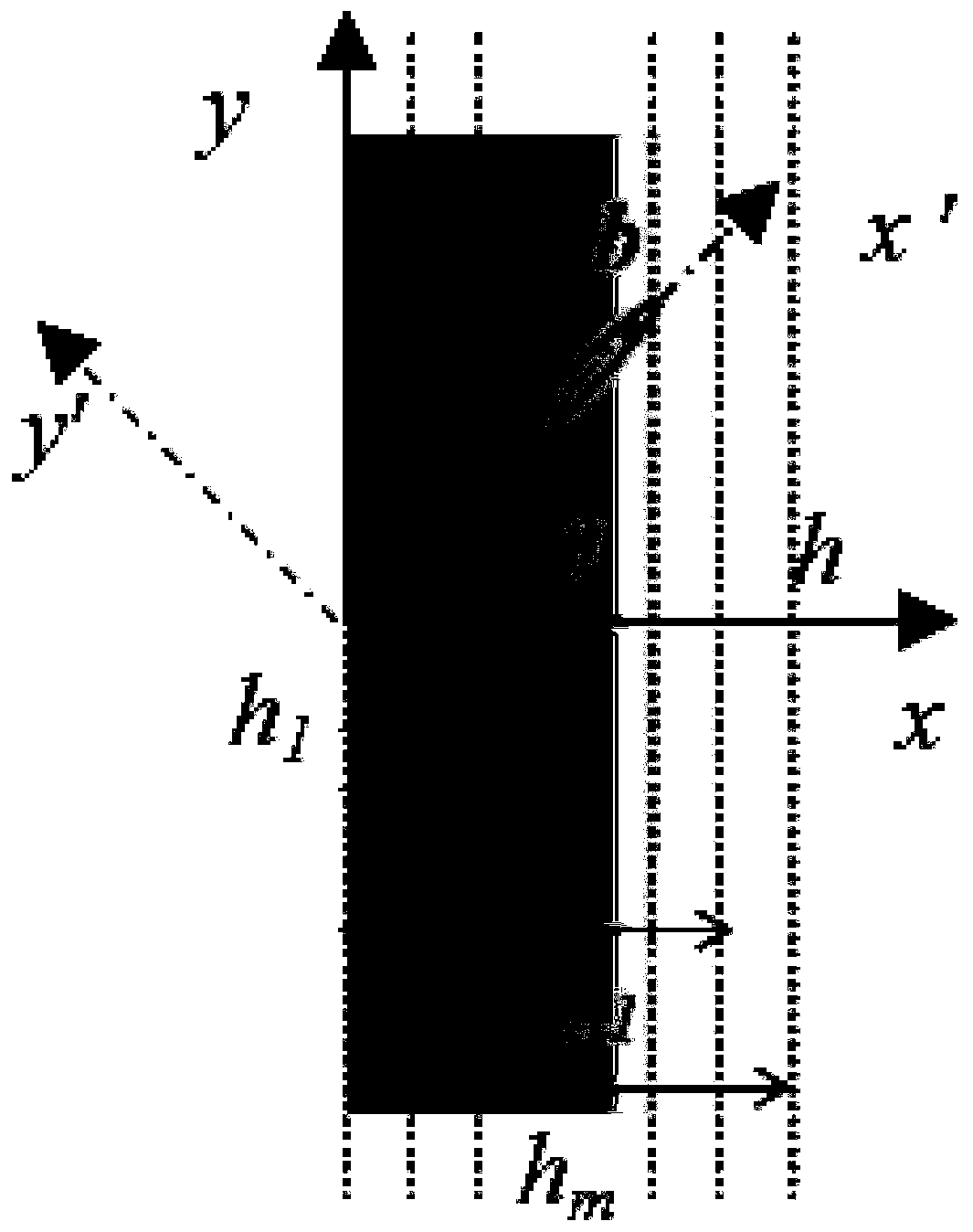
[0040] In view of the arbitrariness of the properties of the functionally graded piezoelectric material, in order to solve the material fracture problem, this embodiment adopts a segmented exponential model.

[0041] The functionally graded piezoelectric material is uniformly divided into m layers along the thickness direction, such as image 3 As shown, the thickness of the nth layer of material is h n –h n-1 , where: n=1,2,…,m,h n Represents the sum of thicknesses from the first layer material to the nth layer material, h n-1 Represents the sum of thicknesses from the first layer material to the n-1th layer material;

[0042] The material properties of each layer are assumed to vary exponentially:

[0043]

[0044] c n44Represents the shear modulus of the nth layer material; e n15 Represents ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for solving a fracture problem of a functionally graded piezoelectric material with any attribute, and belongs to the technical field of fracture mechanics. Accordingto the method, the problems that the obtained crack parameters are inaccurate and the application of an existing solving method is limited due to the fact that the fact that the functionally graded piezoelectric material has any attribute is not considered in solving of the fracture problem of the existing functionally graded piezoelectric material are solved. According to the method, the functionally graded piezoelectric material is divided into a plurality of layers, and the material attributes of each sub-layer are supposed to be distributed in a special function form, namely, a special piecewise function curve is used for approximating a curve of real material attributes of the functionally graded piezoelectric material. Not only can the influence of non-uniform parameters of materialattributes on a crack tip stress field be reflected, but also the influence of the distribution form of the material attributes on the fracture behavior of the functionally graded piezoelectric material can be fully considered, so that the fracture problem of the functionally graded piezoelectric material with any attribute can be solved. The method can be applied to solving the fracture problem of the functionally graded piezoelectric material.

Description

technical field [0001] The invention belongs to the technical field of fracture mechanics, and in particular relates to a method for solving the fracture problem of functionally gradient piezoelectric materials with arbitrary properties. Background technique [0002] So far, piezoelectric materials have played a vital role in emerging technologies, especially in fields such as aerospace, electronics and biology. Because piezoelectric materials have the potential to reduce stress concentration and improve fracture toughness, in order to meet the requirements of piezoelectric materials in terms of life and reliability, functionally graded materials are extended to piezoelectric materials. This kind of material with continuously changing characteristics is called Functionally graded piezoelectric materials. Due to the manufacturing, processing and molding process of functionally graded piezoelectric materials, various cracks and defects occur in them. In recent years, many sc...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/20
Inventor 孔园洁王志海果立成
Owner HARBIN UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com