Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

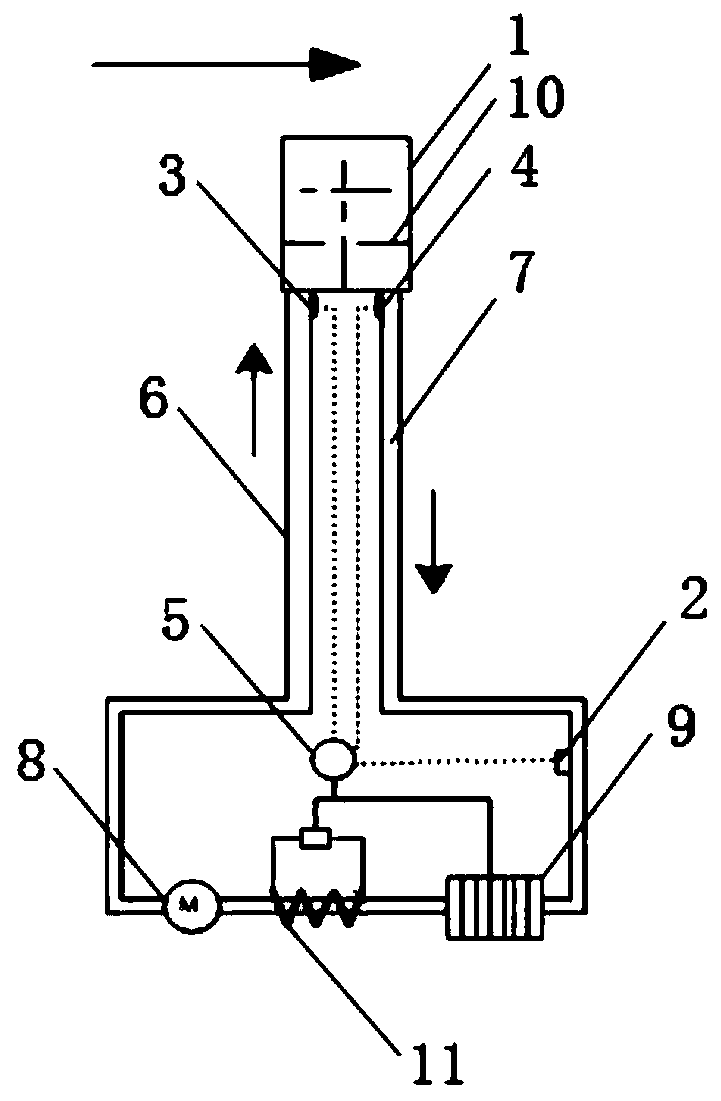
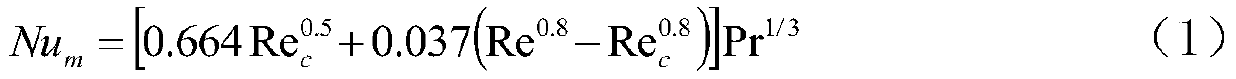Fluid velocity measurement method and device based on convective heat transfer

A technology of fluid flow velocity and convective heat transfer, which is applied in the direction of measuring fluid velocity by using thermal variables. It can solve the problems of easy breakage of hot wires, blockage of measurement holes, and difficult realization of flow velocity direction, and achieve accurate measurement results.

Inactive Publication Date: 2019-07-26
CHINA DATANG CORP SCI & TECH RES INST CO LTD EAST CHINA BRANCH +2
View PDF12 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, these two speed measuring instruments have shortcomings in the work of measuring fluid flow velocity. For example, when measuring the flow velocity with a pitot tube, when the fluid contains a small amount of particles, it may block the measurement hole and affect the measurement. The direction of the flow velocity at the point is also not easy to realize; while the thermal element in the hot wire anemometer is impacted by the airflow from all directions, it will affect the accuracy of the measurement results, and the probe will interfere with the flow field to a certain extent, and the hot wire is easy to break

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fluid velocity measurement method and device based on convective heat transfer
  • Fluid velocity measurement method and device based on convective heat transfer
  • Fluid velocity measurement method and device based on convective heat transfer

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0047] When the part where the measuring probe is in contact with the measured fluid is a plate structure, the following heat transfer formula is listed:

[0048]

[0049]

[0050]

[0051]

[0052] Among them: Pr is the Prandtl number, ν is the kinematic viscosity, λ is the thermal conductivity, L is the measuring probe,

[0053] For steady-state heat transfer, due to the critical Reynolds number Re cis a constant, and for a specific fluid, Prandtl number Pr, kinematic viscosity ν and thermal conductivity λ are only related to temperature, so Prandtl number Pr, kinematic viscosity ν and thermal conductivity λ can be calculated according to T k and T w Obtained, the length L of the measuring probe is known, combined with formulas (1), (2), and (3), we can get That is, the fluid flow rate u corresponds to the heat transfer coefficient h one by one, and the formula (4) is brought into the formula Since the heat transfer area A of the measuring probe and the meas...

Embodiment 2

[0055] When the part where the measuring probe is in contact with the measured fluid is a circular tube structure, the following heat transfer formula is listed:

[0056] Nu m =CRe n PR 1 / 3 (1)

[0057]

[0058]

[0059]

[0060] Among them: Pr is the Prandtl number, ν is the kinematic viscosity, λ is the thermal conductivity, L is the measuring probe, C and n are known constants that can be obtained by looking up the table according to the range of Re;

[0061] The fluid velocity u is calculated by formulas (1), (2), (3), and (4).

Embodiment 3

[0063] When the part of the measuring probe in contact with the measured fluid is a spherical structure, the following heat transfer formula is listed:

[0064]

[0065]

[0066]

[0067]

[0068] Among them: Pr is the Prandtl number, ν is the kinematic viscosity, λ is the thermal conductivity, L is the measuring probe, η k For the measured fluid at temperature T k Dynamic viscosity at , η w For the measured fluid at the wall temperature of the measuring probe T w The dynamic viscosity under , and when the measured fluid type and temperature are known, then η k and η w is a known constant.

[0069] The fluid velocity u is calculated by formulas (1), (2), (3), and (4).

[0070] In addition, in step S3, when the heat transfer between the measuring probe and the measured fluid is a steady-state heat transfer, specifically: within a ΔT time, T k The temperature is constant and the input cooling fluid enters the temperature T of the measuring probe 0 constant.

...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a fluid velocity measurement method and device based on convective heat transfer. The method comprises the steps of: S1, selecting a measurement probe, and enabling the interior of the selected measurement probe to have a flow channel for a medium to flow in and out; S2, conveying constant-temperature cooling fluid into the flow channel, and putting the measurement probe inthe measured fluid; S3, when heat transfer between the measurement probe and the measured fluid is steady heat transfer, obtaining the temperature T<k> of the measured fluid, the surface temperatureT<w> of the measurement probe and the temperature T<2> of the cooling fluid at the outlet end of the flow channel; and S4, obtaining the velocity u of the measured fluid by calculation based on the T<k>, the T<w>, the T<2> and a pre-set formula. The device comprises the measurement probe, a pumping mechanism, a flowmeter, a first temperature meter, a second temperature meter, a third temperature meter and a controller. The method and device in the invention are not interfered by the fluid; blocking of a measurement hole of a Pitot tube and breakage of the hot wire of a hot-wire anemometer do not exist; and measurement is accurate.

Description

technical field [0001] The invention relates to the technical field of velocity measurement, in particular to a method and device for measuring fluid flow velocity based on convective heat transfer. Background technique [0002] At present, the commonly used speed measuring instruments are mainly thermal anemometers and pitot tubes. Since the working principle of the thermal anemometer is to place a thin metal wire (called a hot wire) heated by electricity in the airflow, the heat dissipation of the hot wire in the airflow It is related to the flow rate, and the heat dissipation causes the temperature change of the hot wire to cause the resistance change, and the flow rate signal is converted into an electrical signal. The Pitot tube measures the total pressure and static pressure of the airflow to determine the airflow velocity according to the principle of the Bernoulli equation. However, these two speed measuring instruments have shortcomings in the work of measuring flu...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01P5/10
CPCG01P5/10
Inventor 马启磊韩磊钟文琪
Owner CHINA DATANG CORP SCI & TECH RES INST CO LTD EAST CHINA BRANCH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com