Non-autocorrelation sampling method for large sample space complex probability distribution
A probability distribution, large sample technology, applied in the field of non-autocorrelation sampling of complex probability distribution in large sample space, can solve problems such as efficiency loss, achieve the effect of small I/O amount, eliminate sample autocorrelation, and fast calculation speed
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
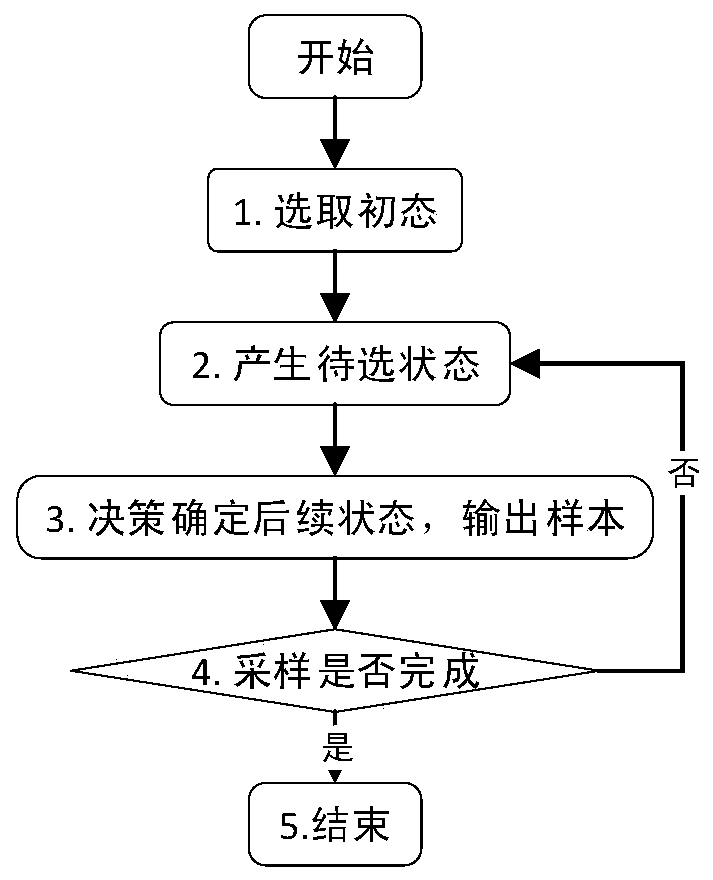
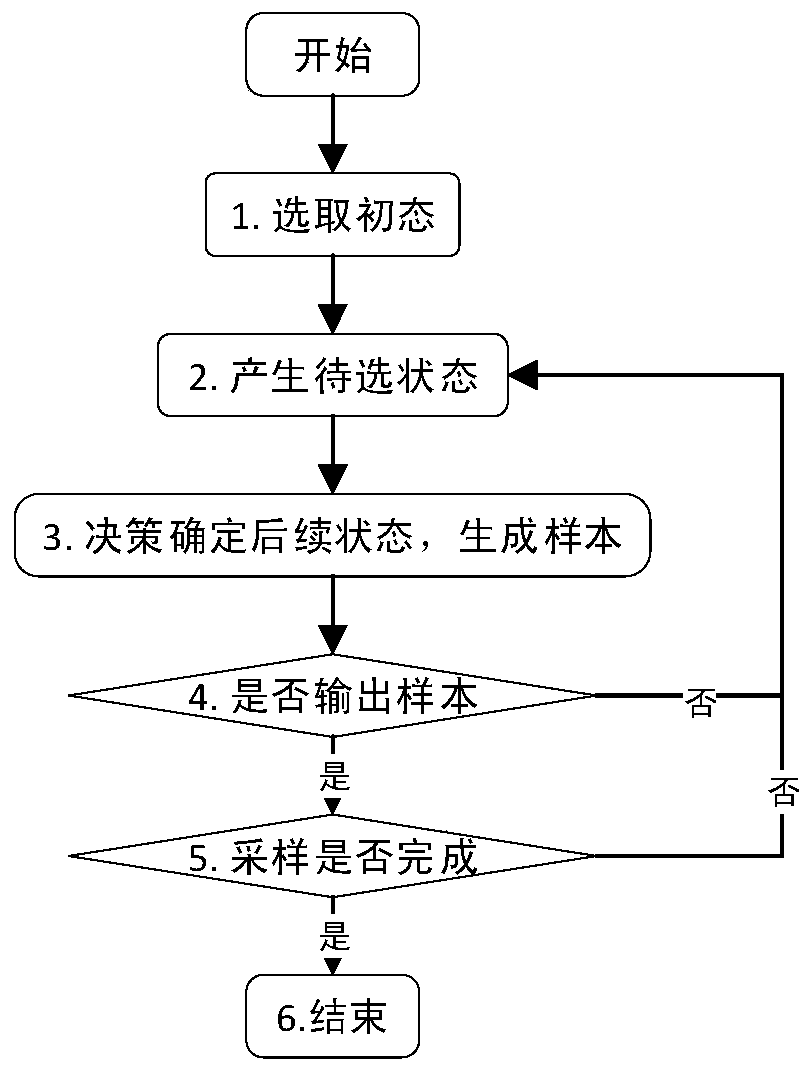
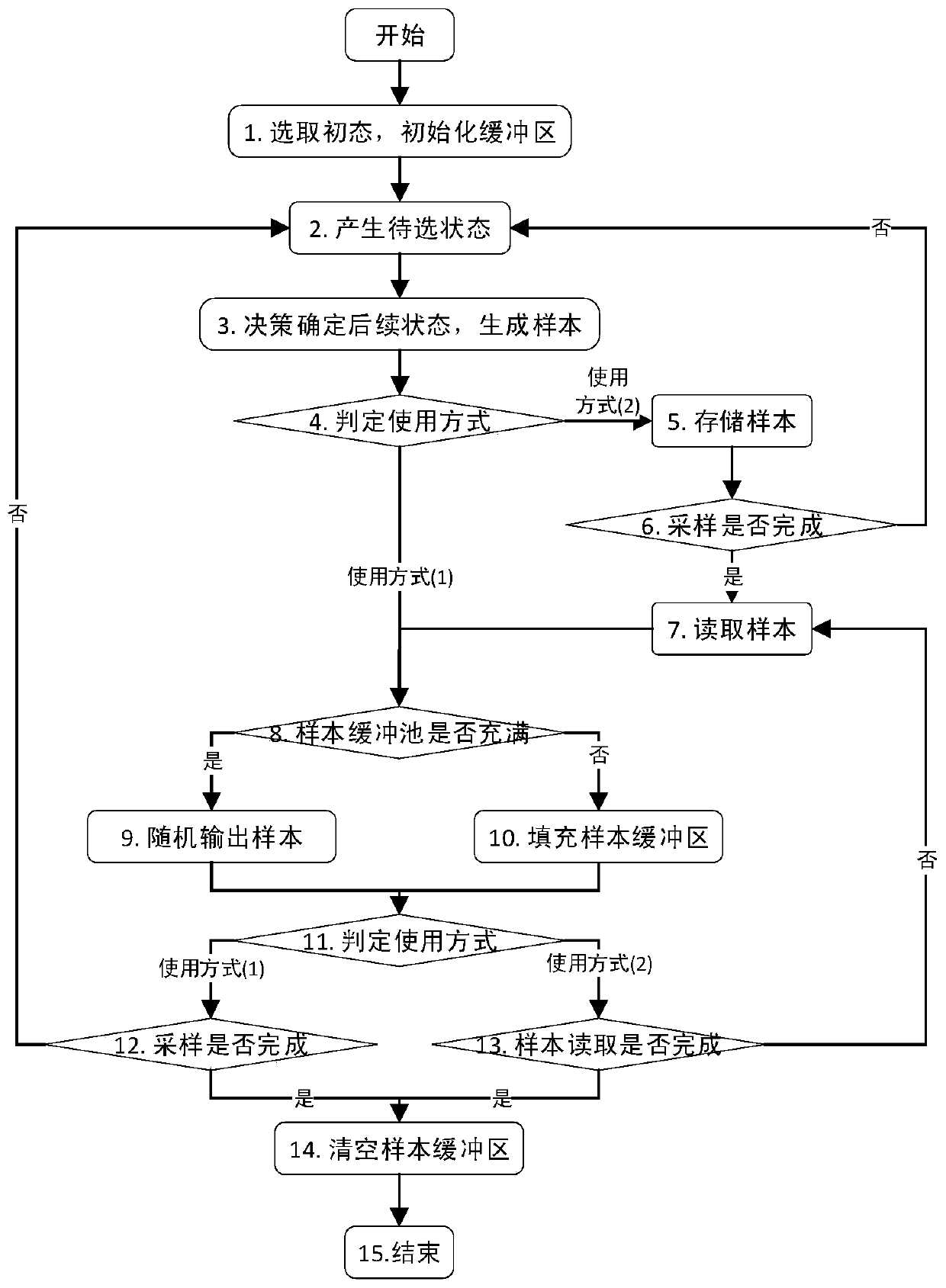
[0129] The overall process of the present invention is as image 3 shown, including the following steps:
[0130] Step 1: Select the initial state and initialize the buffer
[0131] 1.1 Define the state space of the Markov chain as S={s 1 ,s 2 ,...,s i ,...,s N}, where for a positive integer i (1≤i≤N), there is s i and X={x in the sample space 1 ,x 2 ,...,x i ,...,x N} element x i correspond;
[0132] 1.2 Construct the sample probability function f based on the Markov chain state space S s (s), such that for an integer i, f s (s i ) = f(x i ), where f(x i ) means sampling to get sample x i The probability;
[0133] 1.3 Arbitrarily select the easy-to-sample random distribution g(s) on the state space S as the auxiliary probability distribution, where g(s i ) means that the state s obtained by sampling i as a sample probability.
[0134] 1.4 Set the sample buffer capacity L to 4000, initialize the sample buffer to be empty, and the capacity is to accommodate ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D Engineer
- R&D Manager
- IP Professional
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com