Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for constructing pursuit barrier for spacecraft by analysis and method for determining capture and escape areas

A spacecraft and structure technology, which is applied in the field of spacecraft pursuit and escape game path planning, can solve the problems of unfavorable pursuit and escape game motion laws, complex countermeasure models, and difficult countermeasures

Active Publication Date: 2018-09-11
NAT UNIV OF DEFENSE TECH
View PDF6 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

One of the reasons is that the game model is complex: the confrontation is carried out in three-dimensional space, and the movement of the two spacecraft in the pursuit-and-escape game at the same time needs to satisfy the laws of orbital dynamics; When optimizing the control strategy, it is usually necessary to solve complex differential equations
[0005] However, compared with the analytical method, the numerical method is not convenient for quick and easy analysis and calculation, and it is not conducive to directly reflecting the law of motion of the game of chasing and fleeing.
In addition, the application of the boundary barrier obtained by the numerical method also has certain limitations. The analysis of the capture area and the escape area is more limited to the division of the two areas, and it is not suitable for judging whether the current area of ​​the spacecraft is a capture area for a specific countermeasure state. zone or escape zone

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for constructing pursuit barrier for spacecraft by analysis and method for determining capture and escape areas
  • Method for constructing pursuit barrier for spacecraft by analysis and method for determining capture and escape areas
  • Method for constructing pursuit barrier for spacecraft by analysis and method for determining capture and escape areas

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

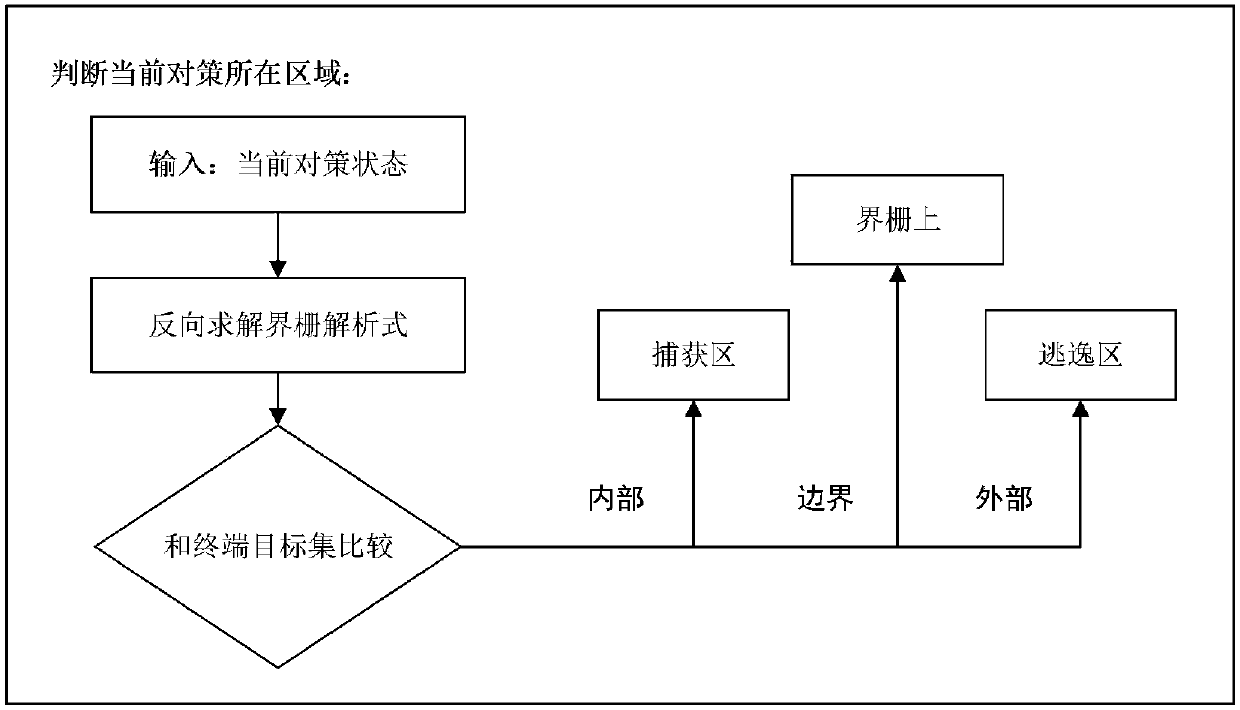
[0099] Such as figure 1 As shown, the steps of a method for analyzing and constructing a boundary barrier for spacecraft chasing and fleeing in this embodiment include:

[0100] S1, using the differential game method to construct the initial model;

[0101] S101, constructing the Hamilton function of the differential game based on the C-W equation,

[0102] 1) Establish the LVLH (Local Vertical Local Horizontal) coordinate system, and construct the motion state equation based on the C-W equation;

[0103] A virtual spacecraft near the two pursued and escaped spacecraft is used as a reference spacecraft to establish a local orbital coordinate system. The origin of the coordinate system is located at the center of mass o of the reference spacecraft, the ox axis is along the radial direction of the reference spacecraft, and the oz axis is along the reference spacecraft The normal direction of the orbital plane of the spacecraft, the y-axis is tangential to the trajectory of the...

Embodiment 2

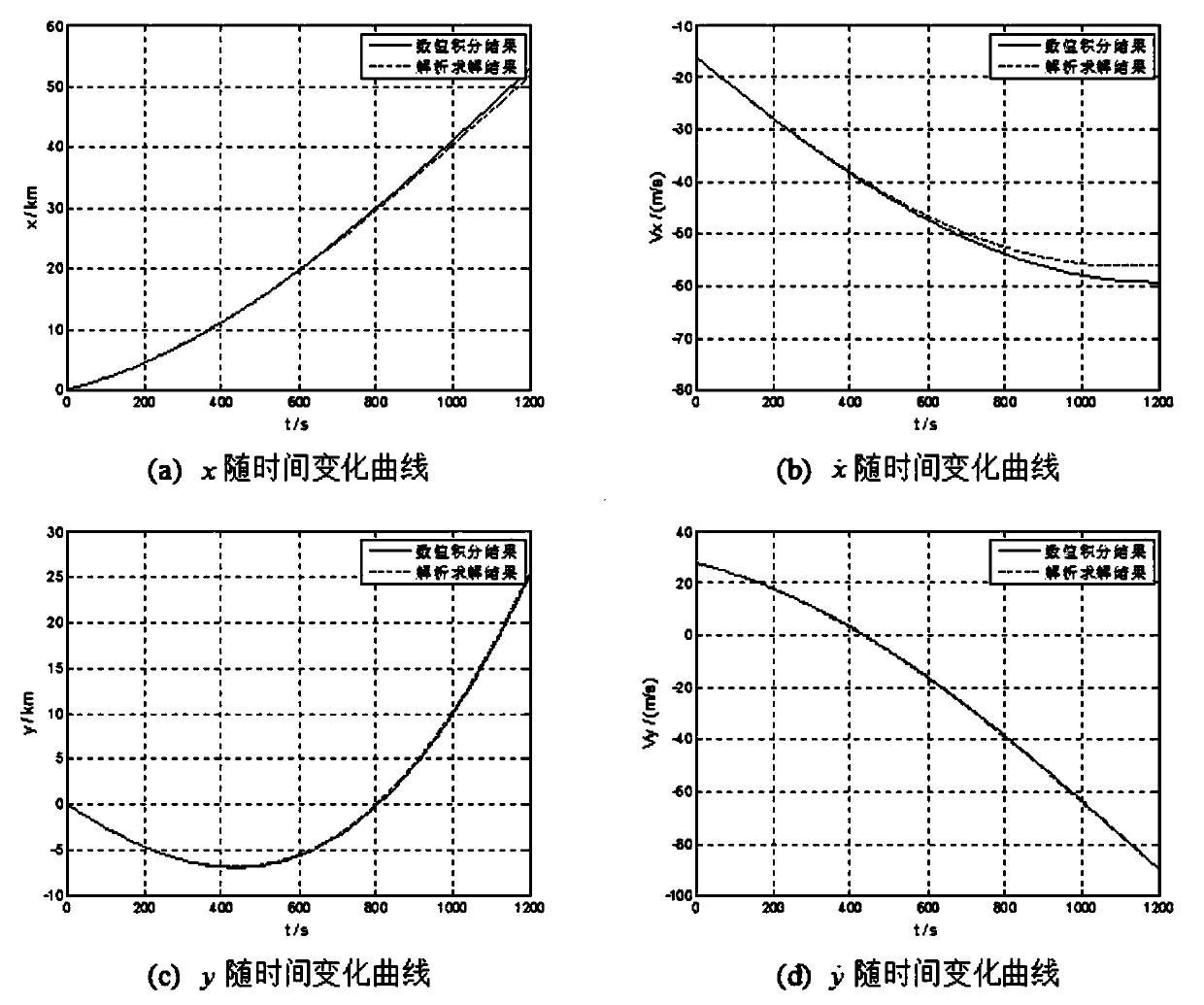
[0161] The steps of this embodiment are basically the same as those of Embodiment 1, and the main difference is that in this embodiment, the azimuth angle of the capture point is no longer a given value, but an independent variable. Therefore, the azimuth angle of different capture points can be obtained by calculation The boundary barrier of the lower differential game at the time τ=1200s.

[0162] Then compare the results of the numerical integration with the results of the analytical solution, see Figure 4 . From the figure, it can be seen that the azimuth Only has a certain impact on the analytical solution accuracy of the position in the y direction of the boundary grid, when or The error is obvious when it is near, but the azimuth angle has little influence on the solution of other boundary grid state quantities.

Embodiment 3

[0164] The steps of this embodiment are basically the same as those of Embodiment 2, the main difference being: in this embodiment, the independent variable is the relative velocity of the capture point

[0165] Figure 5 The relative velocities of different capture points are given in The boundary grid of the calculated strategy at time τ is shown below, and the numerical integration results and analytical solution results are compared. It can be seen from the figure that for different The analytical calculation results are in good agreement with the numerical integration results. At the same time, it can also be seen from the figure that within a given range, the position of the boundary grid in the two directions of x and y varies with decreases with the increase of , while the velocity in both directions increases accordingly.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for constructing a pursuit barrier for a spacecraft by analysis and a method for determining capture and escape areas. The method for constructing the pursuit barrierfor the spacecraft by analysis comprises the following steps: constructing an initial model with a differential game method, solving the initial model and acquiring a barrier analytical solution in order to analyze the pursuit barrier for the spacecraft. By rapidly calculating and analyzing a barrier, a judgment is made clearly as to whether the spacecraft is located in a capture area or an escapearea in the game of pursuit so as to provide a reference for early warning of space threat and game path planning. The design method is accurate and reasonable, rapid and efficient in calculation process and is well fit for a real task.

Description

technical field [0001] The invention relates to a game path planning method for spacecraft pursuit and escape, in particular to a structure of a spacecraft pursuit and escape boundary barrier and a method for judging a capture and escape area. Background technique [0002] Space rendezvous and avoidance maneuver is a key technology of space security. With the increasingly tight space resources, spacecraft will face the threat of being captured or killed by tracking spacecraft in possible space confrontations in the future. When the two spacecraft in the confrontation can make independent decisions and maneuvers, the confrontation becomes a problem of continuous dynamic game in space. [0003] Differential game is a theory that uses differential methods to study infinite dynamic games in continuous time, and is very suitable for modeling and analyzing such problems. When using this theory to qualitatively analyze whether the pursuit and escape can be realized, it involves s...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/13G06F17/11
CPCG06F17/11G06F17/13
Inventor 罗亚中祝海李振瑜孙振江张进
Owner NAT UNIV OF DEFENSE TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com