Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Numerical Calculation Method of Finite Volume Flow Field Based on Non-equidistant Grid

A finite volume, numerical calculation technology, applied in design optimization/simulation, special data processing applications, etc., can solve problems such as reduced accuracy, unstable format, negative linear weight, etc.

Active Publication Date: 2021-07-27
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, once it is extended to non-equidistant grids, its construction is relatively complicated, because its specific expressions are not only related to the physical quantities on the grid points but also related to the grid scale
In addition, whether it is an isometric grid or a non-isometric grid, the linear weight in the above process must be the optimal linear weight to make the overall format achieve the expected design accuracy, otherwise it will reduce the accuracy and even cause negative linear weights to cause the format unstable

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Numerical Calculation Method of Finite Volume Flow Field Based on Non-equidistant Grid
  • A Numerical Calculation Method of Finite Volume Flow Field Based on Non-equidistant Grid
  • A Numerical Calculation Method of Finite Volume Flow Field Based on Non-equidistant Grid

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0150] Embodiment 1, accuracy test problem. Considering the equation group (1), the initial conditions are: ρ(x,y,0)=1+0.2sin(π(x+y)), u(x,y,0)=0.7, v(x,y, 0)=0.3, p(x,y,0)=1. The exact solution is: ρ(x,y,t)=1+0.2sin(π(x+y-t)), u(x,y,t)=0.7, v(x,y,t)=0.3, p( x,y,t)=1. The calculation end time is t=2. The calculation area is (x,y)∈[0,2]×[0,2]. In order to illustrate that the linear weight in the numerical calculation method of the present invention can be arbitrarily selected, the present invention only takes five groups of numbers with different laws as the linear weight: (1) γ 1 =0.98,γ 2 =0.01,γ 3 =0.01; (2)γ 1 =0.495,γ 2 =0.495,γ 3 =0.01; (3)γ 1 =1 / 3,γ 2 =1 / 3,γ 3 = 1 / 3; (4)γ 1 =0.001,γ 2 =0.001,γ 3 =0.998; (5)γ 1 =0.3,γ 2 =0.4,γ 3 = 0.3.

[0151]

[0152]

[0153] Table 1 Comparison of the numerical accuracy of any five linear weights with the traditional WENO format

Embodiment 2

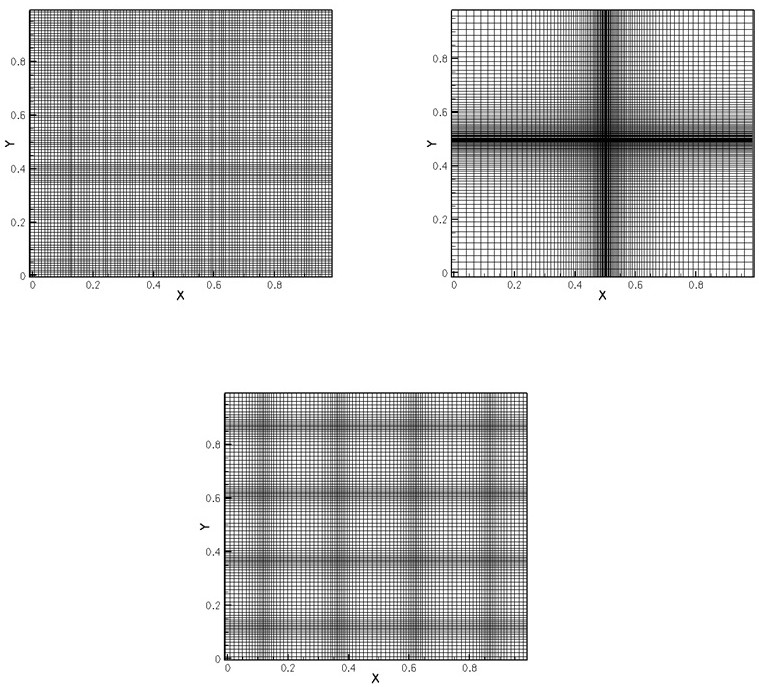
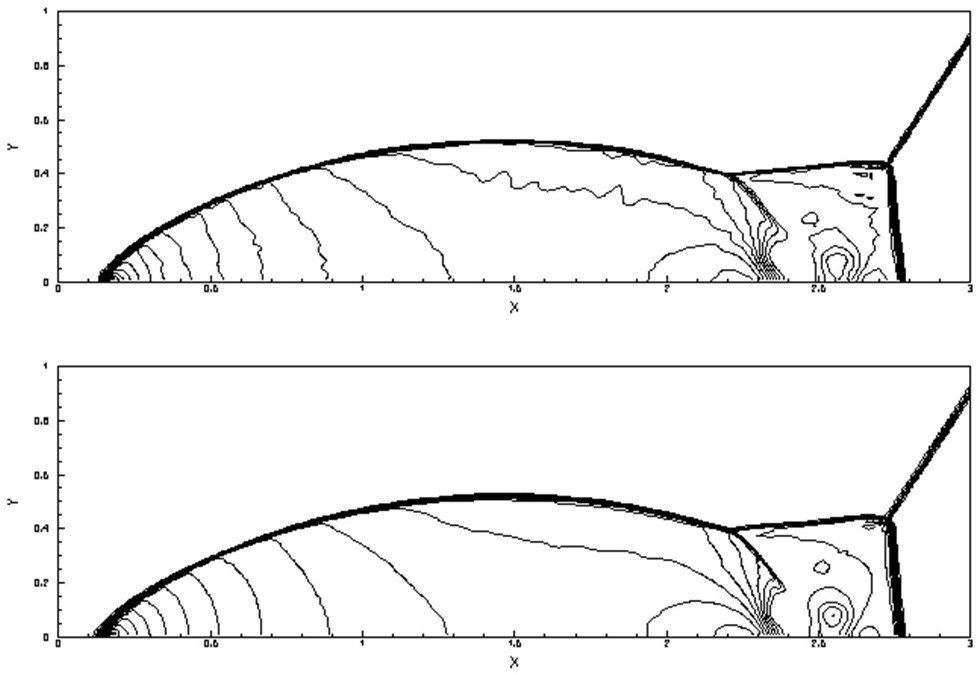
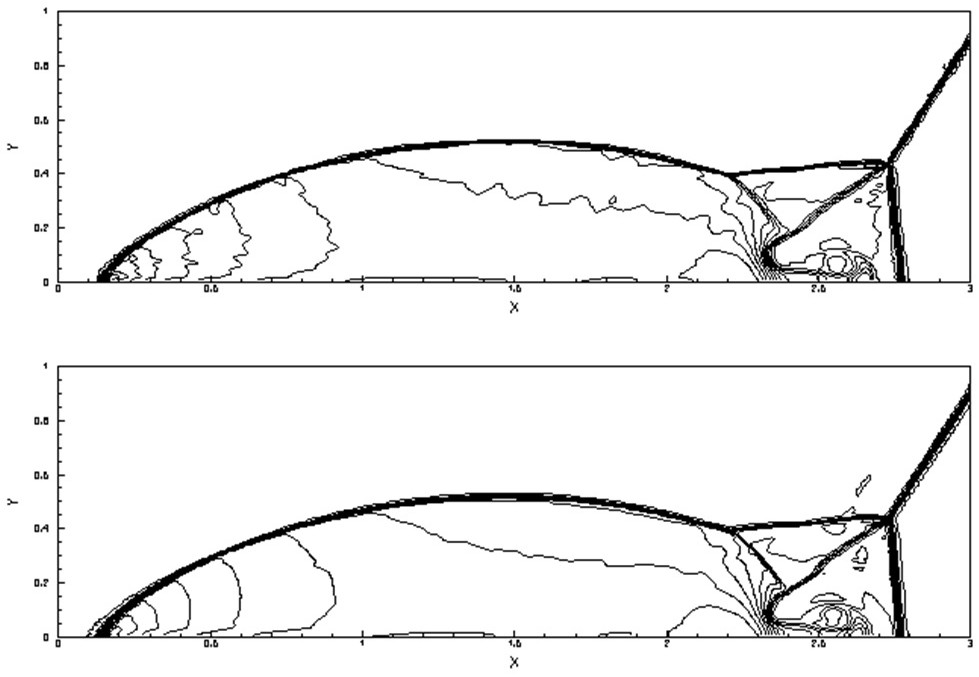
[0154] Embodiment 2, double Mach reflection problem. Such as figure 2 , image 3 As shown, there is a strong shock wave with a Mach number of 10 at 1 / 6 of the left boundary, which is injected at an angle of 60° with the x-axis, and the left and right state values ​​are: (ρ L ,u L ,v L ,E L )=(8,7.145,-4.125,563.544), (ρ R ,u R ,v R ,E R )=(1.4,0,0,2.5). The number of CFL is 0.6, the calculation grid is 300×100, and the end time t=0.2.

Embodiment 3

[0155] Embodiment 3, radial symmetric Riemann problem. Such as Figure 4 As shown, considering the fluid dynamics equations (1), the initial conditions are:

[0156]

[0157] The calculation area is [0,1]×[0,1], the number of CFL is 0.6, the calculation grid is 100×100, and the calculation termination time is t=0.13.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A numerical calculation method for finite volume flow field based on non-equidistant grids, which involves a fifth-order finite volume WENO scheme with linear weights. Without reducing the overall numerical accuracy, only three additive A positive number equal to 1 is used as a linear weight, and then subsequent calculations can be performed. Since the numerical format constructed by the present invention does not need to calculate complex linear weights related to the grid scale under non-equidistant grids, it is easier to extend to higher-order WENO schemes, moving grids, or flow fields in adaptive grids calculate. In addition, the present invention, like the traditional WENO format, uses the Runge-Kutta time-discrete method with good stability, simple operation and easy programming to solve the problem. Finally, the present invention verifies its superiority in flow field calculation by comparing it with the traditional formula through specific numerical examples.

Description

technical field [0001] The invention discloses a finite volume flow field numerical calculation method based on non-equidistant grids, which can be used in computational mathematics, aerodynamics, magnetohydrodynamics, aerospace, missile launching, automobile industry, civil engineering, environmental engineering, ships , meteorological engineering and other technical fields. Background technique [0002] In recent decades, the high-order numerical solution format of hyperbolic conservation law equations has been the key research content, and its application fields include computational fluid dynamics, computational astronomy, semiconductor simulation, traffic flow models, and magnetohydrodynamics. The main difficulty in solving the equations of these problems lies in the complexity of the solution. Even if the initial value is smooth, it will evolve over a period of time to produce complex solution structures such as shock waves, contact gaps, and sparse waves. In addition...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/23
CPCG06F30/20
Inventor 王镇明朱君赵宁
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com