Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

An enhancement method of quasi-cyclic quantum ldpc codes applied to quantum communication systems

A technology of LDPC code and quantum communication, which is applied in the enhanced field of quasi-cyclic quantum low-density parity check LDPC code, which can solve the problems of decreased error correction capability, limited error correction capability, and insufficient number of check bits, etc., to achieve good correction Error performance, the effect of improving versatility

Active Publication Date: 2021-06-04
XIDIAN UNIV
View PDF10 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, for this type of code, as the code length increases, the code rate quickly approaches unity, resulting in limited error correction capability due to the insufficient number of parity bits in long code application scenarios.
[0004] To sum up, the problem existing in the existing technology is: for the existing quasi-cyclic quantum low-density parity check LDPC code, once the code length is determined, the code rate will also be determined accordingly
In the long code application scenario, the code rate will quickly approach 1, which will lead to a decrease in error correction capability due to insufficient number of parity bits in the decoding process
Therefore, this type of quantum code can only be used in short and medium code scenarios

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • An enhancement method of quasi-cyclic quantum ldpc codes applied to quantum communication systems
  • An enhancement method of quasi-cyclic quantum ldpc codes applied to quantum communication systems
  • An enhancement method of quasi-cyclic quantum ldpc codes applied to quantum communication systems

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

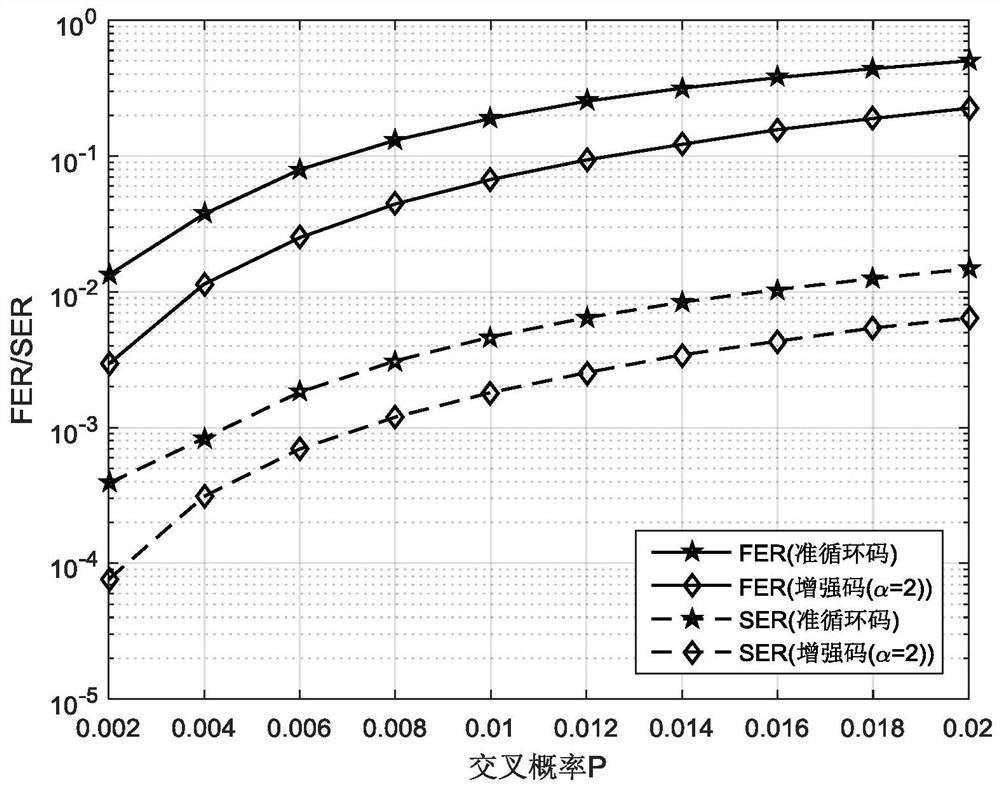
[0076] Embodiment 1, based on Euclidean geometry EG(4,2), construct a quasi-cyclic code with a quantum code rate of 0.75, and then enhance it with an enhancement coefficient α=2 to obtain an enhanced code with a quantum code rate of 0.5. The implementation steps are as follows:

[0077] (1) The parameter m=4 of setting Euclidean geometry, q=2 obtains the quasi-circular matrix H based on Euclidean geometry EG (4,2) EG . This matrix consists of 7 sub-matrices, namely:

[0078] h EG =[H 0 ,H 1 ,H 2 ,H 3 ,H 4 ,H 5 ,H 6 ];

[0079] where each sub-matrix H i Both are a circular matrix of size 15, H i The corresponding generator polynomial is:

[0080] g i (x)=x i+1 +1;

[0081] (2) Since the number of cyclic sub-matrices in step (1) is an odd number, a unit matrix with a size of 15 is concatenated as H 7 , get a new quasi-circulant matrix H;

[0082] (3) Construct quasi-cyclic quantum LDPC codes.

[0083] 3a) Construct the matrix H for correcting the phase error o...

Embodiment 2

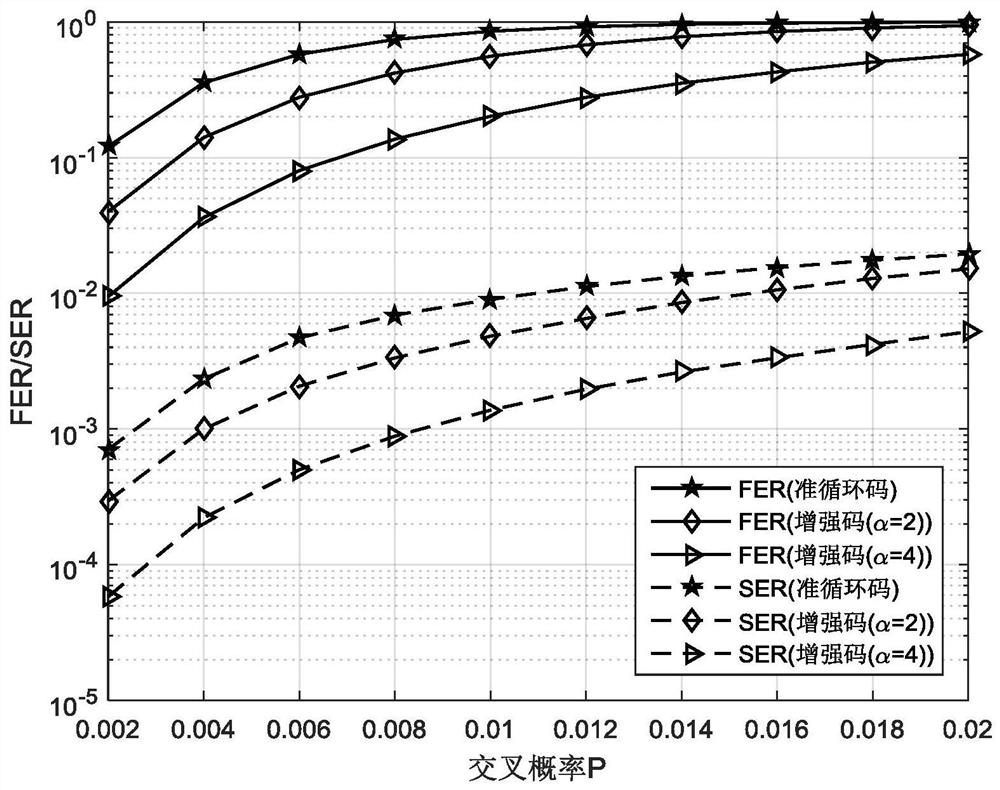
[0106] Embodiment 2, based on Euclidean geometry EG (5,2), construct the quasi-cyclic code of quantum code rate 7 / 8, then do the enhancement of enhancement coefficient α=2 and α=4 to it respectively, obtain quantum code rate 3 Enhanced codes of / 4 and 1 / 2. The implementation steps are as follows:

[0107] (1) Set the parameter m=5 of Euclidean geometry, q=2 obtains the quasi-circular matrix H based on Euclidean geometry EG(5,2) EG . This matrix consists of 15 sub-matrices, namely:

[0108] h EG =[H 0 ,H 1 ,...,H 14 ];

[0109] where each sub-matrix H i Both are a circular matrix of size 31, H i The corresponding generator polynomial is:

[0110] g i (x)=x i+1 +1;

[0111] (2) Since the number of cyclic sub-matrices in step (1) is an odd number, a unit matrix with a size of 31 is concatenated as H 15 , get a new quasi-circulant matrix H;

[0112] (3) Construct quasi-cyclic quantum LDPC codes.

[0113] 3a) Construct the matrix H for correcting the phase error of th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the technical field of quantum communication, and discloses an enhancement method of a quasi-cyclic quantum LDPC code applied to a quantum communication system; it solves the problem of poor error correction performance of the quasi-cyclic quantum LDPC code in a long code application scenario; the present invention Implementation steps of the invention: constructing a quasi-circular matrix H based on Euclidean geometry EG ; to H EG The quasi-circular matrix H with an even number of sub-matrices is obtained by processing; the quasi-cyclic quantum LDPC code is constructed based on H; the column sparse processing is performed on H to construct an enhanced quantum code; BP algorithm is used for decoding. In the present invention, the column sparse processing is performed on the check matrix of the quasi-circular quantum code, so that better error correction performance can be obtained under the condition of the same code length. Extend its application scenarios to the field of long codes.

Description

technical field [0001] The invention belongs to the technical field of quantum communication, and in particular relates to an enhancement method of a quasi-cyclic quantum low-density parity check LDPC (low-density parity-check) code. Background technique [0002] The theory of quantum communication and quantum computing points out the direction for constructing efficient and secure communication systems. However, due to the existence of decoherence phenomenon, the quantum state is easily destroyed, which becomes a problem that must be overcome in quantum communication. For this reason, people put forward the quantum error correcting code theory. Among them, the quantum low-density parity-check LDPC code is a kind of error control code with excellent performance that is very close to the Hash capacity limit, which can improve the reliability of the quantum communication system. [0003] At present, the commonly used existing technology in the industry is to construct two sp...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H03M13/11
CPCH03M13/116
Inventor 王云江王治春石莎刘阳王增斌
Owner XIDIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com