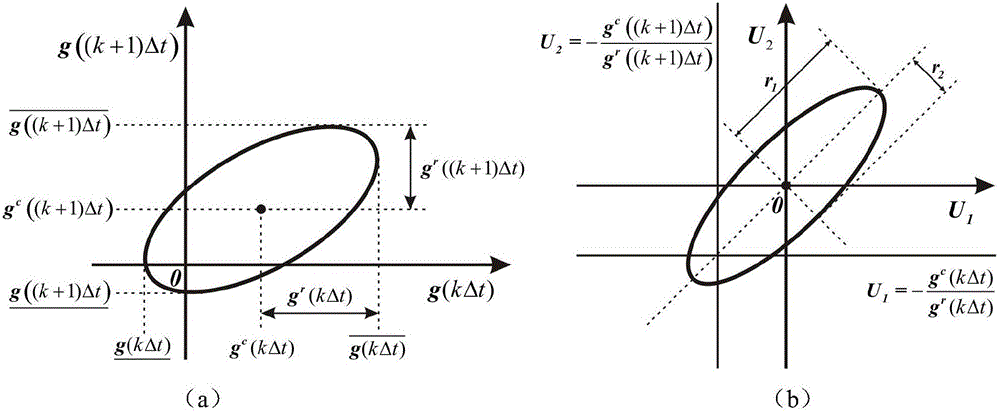In-service structure optimal maintenance design method based on convex model time-variation reliability
A technology of optimal structure and maintenance design, applied in computing, instrumentation, data processing applications, etc., can solve the comprehensive impact of maintenance effects and the refinement of constraints due to redundant maintenance and reinforcement methods, failure to effectively account for time-varying uncertainty effects Maintenance design, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment
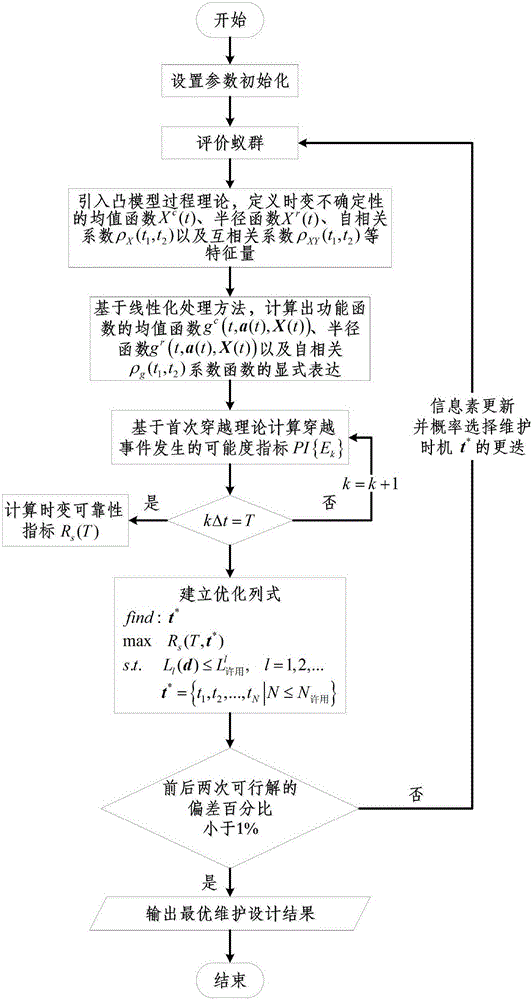
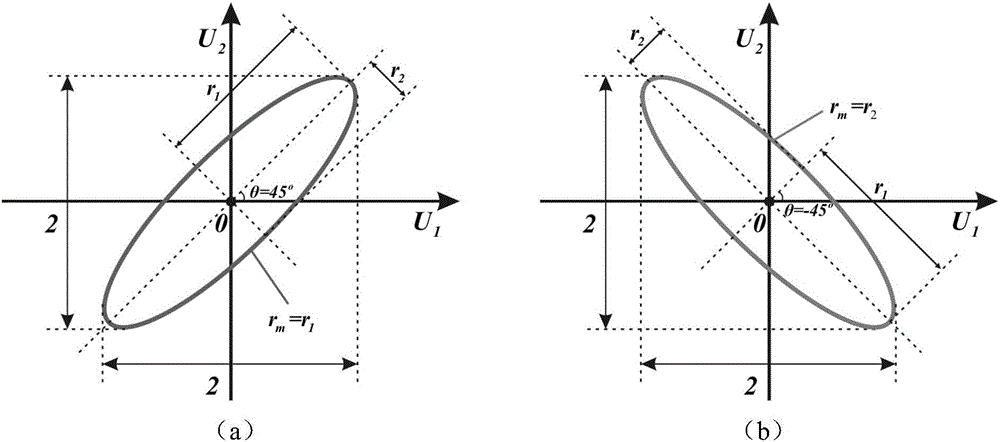
[0086] In order to understand more fully the characteristics of the invention and its applicability to engineering practice, the present invention aims at such as Figure 5 Optimal scheme design for single-maintenance reinforcement of the 24-layer composite laminate structure shown in service. It adopts a symmetrical lay-up scheme [θ / θ / θ / θ / θ / θ / -θ / -θ / -θ / -θ / -θ / -θ] 对称 . The structure is subject to a concentrated load acting at the geometric center and is restrained by four-sided braces. The length l and width b of the board are both 100mm, and the thickness of each layer of board is t=0.147mm. The laminate material has transverse isotropy, and its density is ρ=1.38×10 3 kg / m 3 . The engineering strength parameter information of the laminate is shown in Table 1, and Table 2 lists the non-probabilistic static and dynamic uncertainty characteristics of the laminate modulus.
[0087] Table 1
[0088]
[0089] Table 2
[0090]
[0091] The two ply types of θ=15° and θ=45...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - Generate Ideas
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com