Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

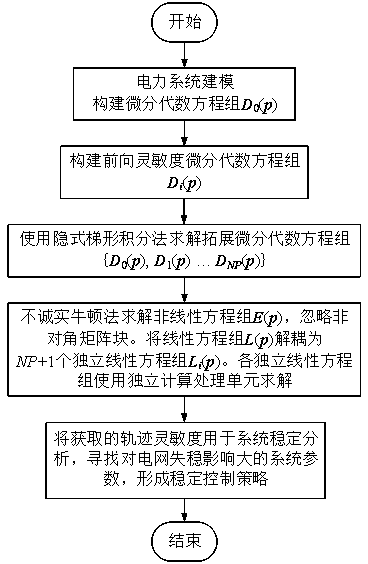
Method for obtaining power system parallelization track sensitivity

A trajectory sensitivity, power system technology, applied in electrical digital data processing, special data processing applications, instruments, etc., can solve problems such as accelerated solutions

Active Publication Date: 2014-09-10
ZHEJIANG UNIV
View PDF5 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the calculation of trajectory sensitivity is essentially a sequential and serial calculation process, and parallel computing technology cannot be directly applied to accelerate the solution.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for obtaining power system parallelization track sensitivity
  • Method for obtaining power system parallelization track sensitivity
  • Method for obtaining power system parallelization track sensitivity

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

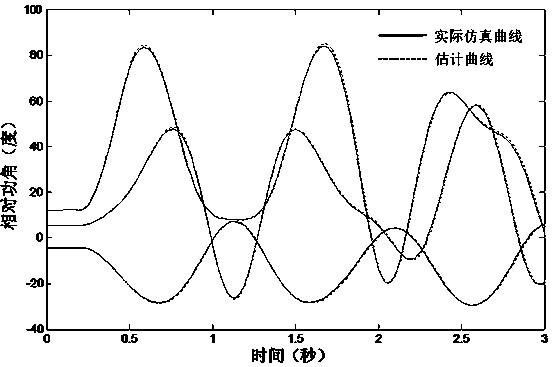
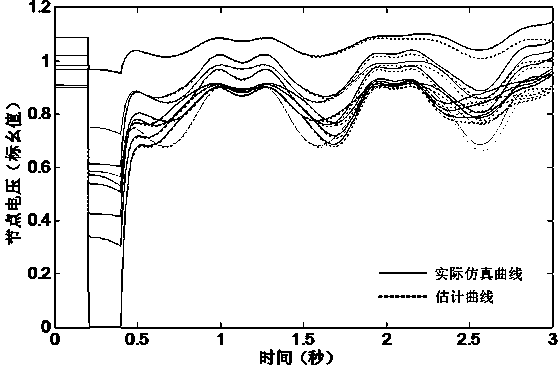
[0082] A simplified nine-node power system CASE9 example is used to verify the validity of the algorithm and the accuracy of the calculation results. One application of trajectory sensitivity is to use the reference trajectory to estimate the trajectory of the neighborhood in the parameter space, namely:

[0083] x(p 0 +Δp,t)≈x(p 0 ,t)+Δp·s(p 0 ,t) \*MERGEFORMAT(5)

[0084] where s(p 0 ,t) is the trajectory sensitivity under the reference parameter vector p0, Δp is the disturbance in the parameter space, x(p 0 ,t) is the reference trajectory. The disturbed trajectory x(p 0 +Δp,t) can be estimated using the above information. Corresponding to the test system, Δp is set to reduce the output of a certain generator by 10MW. figure 2 and image 3 Two calculation methods for post-disturbance trajectories (including generator power-angle curves and system node voltage curves) are demonstrated, namely using full time-domain simulations and using trajectory sensitivity estima...

Embodiment 2

[0086] A standard power system test system CASE678 is used to test the computational efficiency and parallel speedup of this method. In order to verify the calculation efficiency of this method in large-scale calculation examples, all initial values ​​of differential algebraic equations are selected as parameter vectors to be analyzed, thereby increasing the amount of calculation used in the test and more realistically simulating the trajectory sensitivity in Application scenarios in the dynamic performance evaluation of actual power systems.

[0087] Table 2 shows the calculation time of two key calculation links in the trajectory sensitivity analysis: the function call link of differential algebraic equations (referred to as function call), and the difference and Newton iteration link of differential algebraic equations solution (referred to as time domain emulation). At the same time, in order to test the scalability of this parallel computing method on a large-scale paral...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for obtaining power system parallelization track sensitivity. Track sensitivity has important application value in the fields of power system dynamic performance assessment, stable verification and control and the like, but in large-scale power system analysis, the technical difficulty that calculation time is excessively long exists and accordingly track sensitivity cannot be effectively applied in an existing power system based on real-time control. To solve the preceding problem, the novel method for obtaining power system track sensitivity more quickly by means of a parallel computing technique is put forward. By digging and making use of the Newton iteration matrix structure property in forward sensitivity analysis, a special dishonest Newton iteration strategy is designed, linear equation systems in Newton iteration can be decoupled and deployed on different computing processing units to be calculated, parallelization of track sensitivity obtaining is achieved, computational efficiency is greatly improved and the method can be used for the fields of power system stable analysis and control and the like.

Description

technical field [0001] The invention belongs to the technical field of operation, analysis and scheduling of electric power systems, and in particular relates to a method for obtaining track sensitivity of electric power systems based on parallel computing technology. Background technique [0002] With the advancement of my country's strong and smart grid construction process, the UHV power grid with Sanhua Power Grid as the core is gradually formed, and a large number of renewable energy sources are connected to the grid for power generation. The dynamic performance of the power system is becoming more and more important in the safe and stable operation of the power grid. The dynamic performance of the power system is usually evaluated and verified by power system time-domain simulation. However, due to the inaccurate model parameters and frequent changes in operating points of modern power systems, it generally requires a large number of time-domain simulations to effective...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F19/00
Inventor 耿光超江全元李志浩
Owner ZHEJIANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com