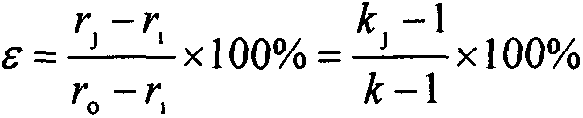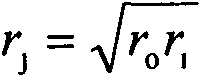A constant-strength self-reinforcing pressure vessel with variable structural dimensions
A technology for pressure vessels and structural dimensions, which is applied in the process industry and mechanical science and technology fields, and can solve problems such as inability to obtain reasonable structures, inability to reflect the essence of problems, inability to obtain structurally variable pressure vessels, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
[0155] Example 1, assuming that a certain pressure vessel intends to withstand 0.5σ y The load of n=0.5-0.5 , 3 -0.5 n=0.866 , the diameter ratio determined by formula (19) is equal to the diameter ratio determined by formula (32). k=1.541896(e 0.5 ), from formulas (33), (32) and (19), λ=1.494745 (1.581977) (the highest).
[0156] (1) λ=1, then k=2.732051 (∞, meaningless) from formula (32). And according to formula (19), when λ=1, k=1j =1, that is, no self-enhancement processing is performed. Containers with such structural parameters are non-self-reinforcing containers. It is thicker.
[0157] (2) λ = 1.2, then k = 1.895544 (2.44949) from formula (32). And according to formula (19), when λ=1.2, k=1.208jλ = 1.11018 (1.10765). That is, the structural parameter of the container is k=1.895544 (2.44949), k jλ = 1.11018 (1.10765). This is a reduction in thickness from case (1) where k 1 、k 2 are the diameter ratios before and after reduction, respectively.
[0158] Th...
Embodiment 2
[0177] Embodiment 2, assume that a certain container intends to bear the load of 0.8σy, namely Or λ≥2n=1.6(III) (lowest). based on the above analysis, , the diameter ratio determined by formula (19) is equal to the diameter ratio determined by formula (33). k=1.999346(e 0.8 ), from formulas (33), (32) and (19), λ=1.847923 (2.004753) (the highest).
[0178] (1) λ=1.4 (the third intensity theory requires λ≥1.6, and there is no third intensity theory result when λ=1.4), then k=9.874078 is obtained from formula (32). And according to formula (19), when λ=1.4, k=1.430048 (see specification attached image 3 point b) jλ = 1.221987. That is, the structural parameter of the container is k=9.874078, k jλ = 1.221987.
[0179] Equivalent residual stress
[0180] Plastic zone (1≤x≤1.221987): σ e ' / σ y From -0.4 on the inner wall monotonously increases to 0.062 on the elastic-plastic interface, safe.
[0181] Elastic zone (1.221987≤x≤9.874078): σ e ' / σ y From 0.062 at the el...
Embodiment 3
[0204] Example 3, assuming a pressure vessel intended to withstand σ y load, that is, n=1>3 -0.5 ,due Or λ≥2n=2(III) (lowest). based on the above analysis, , the diameter ratio determined by formula (19) is equal to the diameter ratio determined by formula (32). When k=2.377443(e), it can be obtained from formulas (33), (32) and (19), λ=2.104356(2.313035) (the highest).
[0205] (1) λ=1.8 (there is no result of the third intensity theory), then k=5.146881 can be obtained from formula (32). And according to formula (19), when λ=1.8, k=1.93322jλ = 1.504974. That is, the structural parameter of the container is k=5.146881, k jλ = 1.504974.
[0206] Equivalent residual stress
[0207] Plastic zone (1≤x≤1.504974): -0.8≤σ e ' / σ y ≤0.21, safe.
[0208] Elastic zone (1.504974≤x≤5.146881): 0.018≤σ e ' / σ y ≤0.21, safe.
[0209] Equivalent total stress
[0210] Plastic zone (1≤x≤1.504974): σ e ≡σ y ,Safety.
[0211] Elastic zone (1.504974≤x≤≤5.146881): 0.086≤σ e / σ ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com