Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

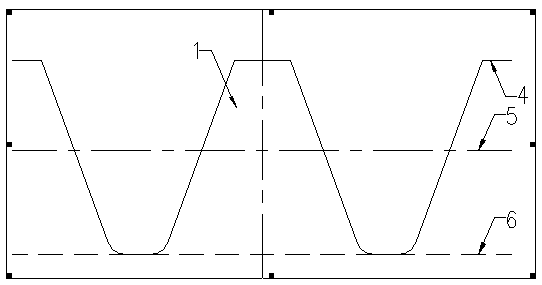
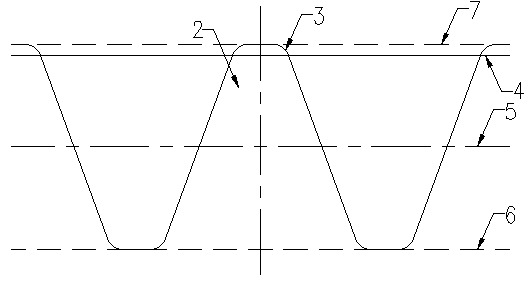
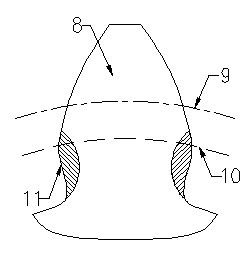
Method for eliminating undercut of involute gear

A technology of involute gears and involutes, applied to components with teeth, belts/chains/gears, portable lifting devices, etc., can solve the problem of reduced coincidence, inability to reduce or eliminate defects of involute gears, Reduce transmission accuracy and other issues

Inactive Publication Date: 2013-08-07
KUNMING UNIV OF SCI & TECH
View PDF11 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The above two known inventions each provide a method for detecting defects in involute gears in use engineering, which has certain guiding significance for discovering problems in gear design, but cannot reduce or eliminate the involute gears in the transmission process. defects in
The method involved in the above-mentioned known invention can eliminate the undercut problem, but this method will cause poor interchangeability of the involute gear mechanism, reduce the transmission accuracy, and make the involute gear tooth tip become sharper, and the coincidence degree is reduced, thereby Causes a decrease in flexural strength and contact strength

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for eliminating undercut of involute gear
  • Method for eliminating undercut of involute gear
  • Method for eliminating undercut of involute gear

Examples

Experimental program
Comparison scheme
Effect test

Embodiment approach 1

[0054] Embodiment 1: In this embodiment, the method for eliminating the undercut of the involute gear firstly calculates the minimum number of teeth for which the involute gear does not undercut:

[0055] When processing standard spur involute cylindrical gears, the modulus m is 5, , and , the minimum number of teeth without undercutting is:

[0056]

[0057] When machining standard helical involute cylindrical gears, , , and , the minimum number of teeth without undercutting is:

[0058]

[0059] When machining standard spur involute bevel gears, due to the head clearance coefficient Set to 0.2. Equivalent of involute bevel gear Minimum number of teeth of straight involute cylindrical gear , when , , by the formula:

[0060]

[0061] Then the minimum number of teeth of the standard involute spur bevel gear without undercutting for:

[0062]

[0063] in, , .

[0064] After calculation, the data are shown in Table 1.

[0065] Table 1 ...

Embodiment approach 2

[0068] Embodiment 2: In this embodiment, the method for eliminating the undercut of the involute gear first calculates the minimum number of teeth for which the involute gear does not undercut:

[0069] When processing short-toothed involute spur gears, the modulus m is 5, , and , the minimum number of teeth without undercutting is:

[0070]

[0071] When machining short-toothed involute helical cylindrical gears, , , and , the minimum number of teeth without undercutting is:

[0072]

[0073] When machining short-toothed involute straight bevel gears, due to the top clearance coefficient Set to 0.2. The equivalent of the involute bevel gear, the minimum number of teeth of the involute spur gear without undercutting is equal to ,at this time , , by the formula:

[0074]

[0075] Then the minimum number of teeth of the short-toothed involute spur bevel gear without undercutting for:

[0076]

[0077] in, , .

[0078] After calculation,...

Embodiment approach 3

[0082] Embodiment 3: In this embodiment, the method for eliminating undercutting of involute gears firstly calculates the minimum number of teeth of involute gears without undercutting:

[0083] For involute gears with pressure angles of 14.5°, 22.5°, and 25°:

[0084] When processing straight involute cylindrical gears, the modulus m is 5, , and , the minimum number of teeth without undercutting is:

[0085]

[0086] When machining helical involute cylindrical gears, , , and , the minimum number of teeth without undercutting is:

[0087]

[0088] When machining straight involute bevel gears, due to the head clearance coefficient Set to 0.2. Equivalent of involute bevel gear Minimum number of teeth of involute spur gear ,at this time , , by the formula:

[0089]

[0090] Then the minimum number of teeth of straight involute bevel gear without undercutting for:

[0091]

[0092] in, , .

[0093] After calculation, the data are shown ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a method for eliminating undercut of an involute gear, and belongs to the technical field of transmission designs and manufacture of involute gears in mechanical equipment. Firstly, the minimum number of teeth which cannot cause undercut of the involute gear is calculated, and a calculation formula of the minimum number of the teeth which cause no undercut during processing is obtained when the involute gear is a straight toothed spur gear, a helical gear or a straight tooth bevel gear respectively; and then the involute gear is processed according to a calculation result, so that the involute gear without the undercut is obtained. The method can eliminate harms of intensity reduction caused by undercut.

Description

technical field [0001] The invention relates to a method for eliminating undercutting of involute gears, in particular to a method for eliminating undercutting of involute gears during tooth cutting, which belongs to the design and manufacturing technology of involute gear transmission in mechanical equipment field. Background technique [0002] As a part for transmitting motion and power, involute gear is the most widely used transmission mechanism in modern machinery. Since Euler founded the theory of involute cylindrical gear in 1765, it has a history of more than 200 years. Gears are the most used transmission parts. Involute gear transmission products are the main body of transmission in the fields of automobiles, shipbuilding, aviation, etc., and are used to transmit motion and power between any two axes in space. Industrial involute gear transmission products are the main transmission components of almost all mechanical complete sets of equipment, occupying about 60...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): F16H55/17G06F19/00
Inventor 何家宁高永张伟张超
Owner KUNMING UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com