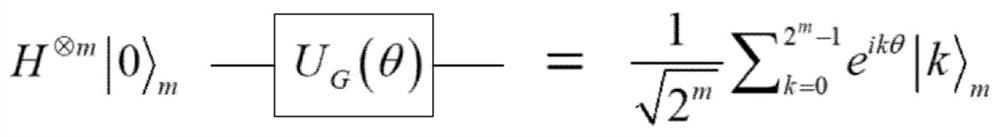Binary integer coefficient polynomial unconstrained optimization method based on Grover search algorithm
An unconstrained optimization and search algorithm technology, applied in the field of binary integer coefficient polynomial unconstrained optimization, can solve problems such as search space constraints, reduce demand, improve multi-objective combinatorial optimization problems, and reduce the number of qubits and quantum gates Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0027] The technical solutions of the present invention will be described in further detail below through specific implementation methods.
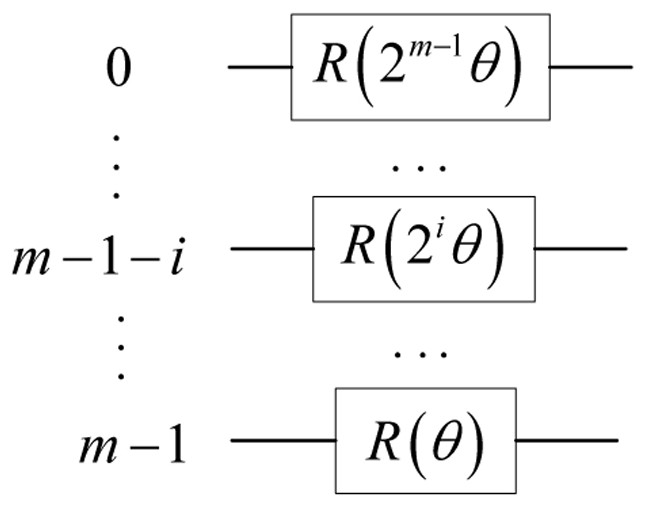
[0028] The Oracle operator is denoted as O, so that every calculation ground state other than |0> obtains a phase shift of -1 to obtain And the probability of the target state is obtained through repeated iterations.
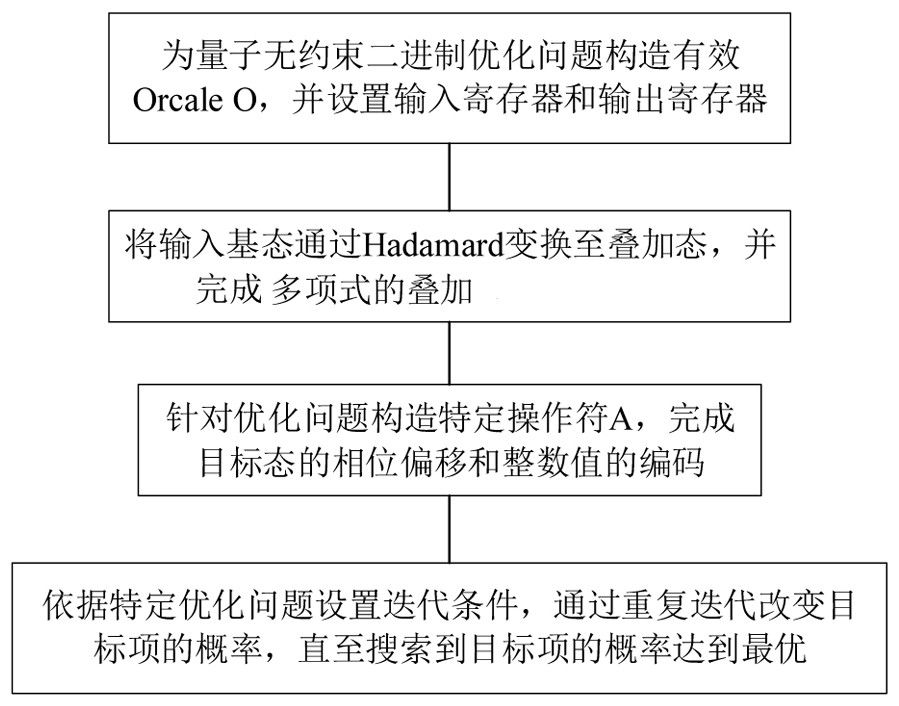
[0029] like figure 1 As shown, a binary integer coefficient polynomial unconstrained optimization method based on Grover's search algorithm includes the following steps:
[0030] Convert the integer coefficient polynomial f(x) of n binary variables into a binary integer coefficient matrix polynomial: f(x)=x T Qx+b T x+c, Q ∈ R n×n is a binary integer coefficient matrix, b∈R n is a vector, c∈R is a constant; x is a variable vector;
[0031] Transform the unconstrained optimization problem of a matrix polynomial with binary integer coefficients into a quantum quadratic unconstrained binary optimization problem: Among...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D Engineer
- R&D Manager
- IP Professional
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com