Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Sparse linear array radar arraying method based on low-rank Hankel matrix completion

A matrix completion and matrix technology, applied to sparse arrays. field, it can solve the problems of large amount of calculation and large dependence on the reference pattern, and achieve fast convergence, saving degrees of freedom, and good results

Active Publication Date: 2022-04-05
UNIV OF ELECTRONICS SCI & TECH OF CHINA
View PDF20 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In MPM, it is necessary to rely on the reference pattern, uniformly sample it, and approach all sampling points on the reference pattern. In this way, the dependence on the reference pattern will be relatively large, and the need to approach many sampling points will result in a large amount of calculation. bigger

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Sparse linear array radar arraying method based on low-rank Hankel matrix completion
  • Sparse linear array radar arraying method based on low-rank Hankel matrix completion
  • Sparse linear array radar arraying method based on low-rank Hankel matrix completion

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

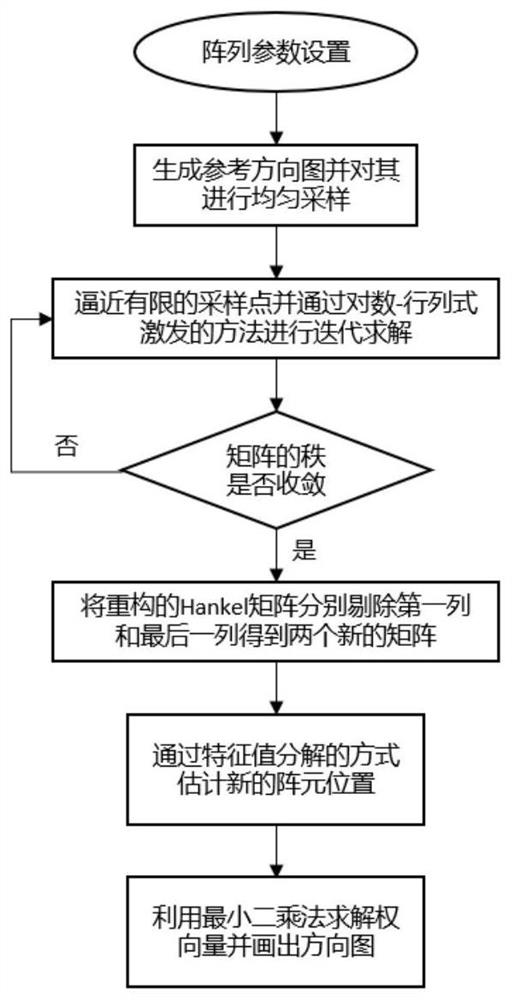
[0052] refer to figure 1 , the specific implementation steps of the present invention are as follows:

[0053] Step 1, construct an initial reference pattern and uniformly sample it.

[0054] Consider a uniform linear array radar with the number of array elements M, and express the pattern of the uniform linear array radar, namely:

[0055]

[0056] Among them, u=sinθ, θ represents the angle, and uniform sampling of f(θ) can be obtained;

[0057] x(n)=F(u)| u＝nΔ

[0058] where n=-N,-N+1, . . . , N.

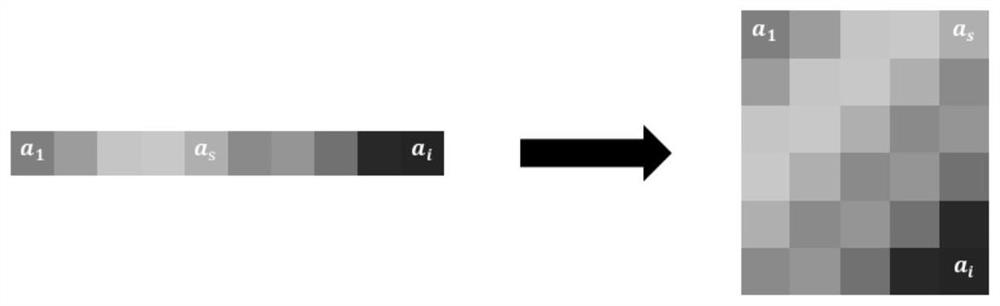
[0059] Constructs the Hankel matrix Y.

[0060] First, refer to figure 2 , define a Hankelization formula:

[0061]

[0062] Then, the following Hankel matrix is ​​constructed by using the sampling points of the reference pattern:

[0063]

[0064] Wherein L is a matrix beam parameter, and satisfies 2N-L≥M, L+1≥M.

[0065] Step 2: Construct an optimization objective function for rank minimization

[0066] 2a) From matrix beam theory, we get:

[0067] rank(Y)=M...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a sparse linear array radar arraying method based on low-rank Hankel matrix completion, and belongs to the field of array radar signal processing. A Hankel matrix is constructed and low-rank completion is carried out on the Hankel matrix, so that an ideal directional diagram is generated and sparse arrangement is realized. According to the method provided by the invention, only a few sampling points on a main lobe need to be approached, and only an upper limit level needs to be set for a side lobe region, so that the number of array elements is reduced, and meanwhile, the dependence on a reference directional diagram and the calculation amount can be reduced to a certain extent. Compared with a matrix pencil method (MPM), the method has the advantages that all sampling points do not need to be approached, the degree of freedom can be saved, only individual sampling points on a main lobe are selected for approaching, and an integral level constraint is applied to a side lobe, that is, elements on an anti-diagonal line of a Hankel matrix are constrained, so that the degree of freedom can be reduced; therefore, an optimization problem of rank minimization is constructed.

Description

technical field [0001] The invention belongs to the field of array radar signal processing, and in particular relates to a method of utilizing low-rank Hankel matrix complementation to generate ideal directions and at the same time realize sparse array arrangement. Background technique [0002] Antennas can be seen everywhere in daily life. Among them, array antennas are popular in engineering applications due to their strong directivity and high gain characteristics, and array signal processing, as an important branch of signal processing, is widely used in radar detection, wireless communication, geological Exploration and many other military and civilian aspects have a wide range of applications. As people have higher and higher requirements for the information processing capabilities of the array antenna in the radar system, the optimal design of the array antenna becomes particularly important. Because the uniform linear array with half-wavelength spacing faces problem...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S7/02H01Q21/00
CPCY02A90/10
Inventor 张学敬顾天元庄杨婧之何子述
Owner UNIV OF ELECTRONICS SCI & TECH OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com