Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Linear frequency modulation signal sparse sampling and reconstruction method based on fractional Fourier transform domain

A technology of linear frequency modulation signal and fractional Fourier, which is applied in the direction of frequency modulation carrier system, code conversion, complex mathematical operations, etc., and can solve problems such as powerlessness

Active Publication Date: 2020-08-28
HARBIN INST OF TECH
View PDF1 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the existing analog information conversion technology is only suitable for multi-spectral or multi-band band-limited sparse signals in the frequency domain, and is powerless for those signals that are not band-limited in the frequency domain

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Linear frequency modulation signal sparse sampling and reconstruction method based on fractional Fourier transform domain
  • Linear frequency modulation signal sparse sampling and reconstruction method based on fractional Fourier transform domain
  • Linear frequency modulation signal sparse sampling and reconstruction method based on fractional Fourier transform domain

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment 1

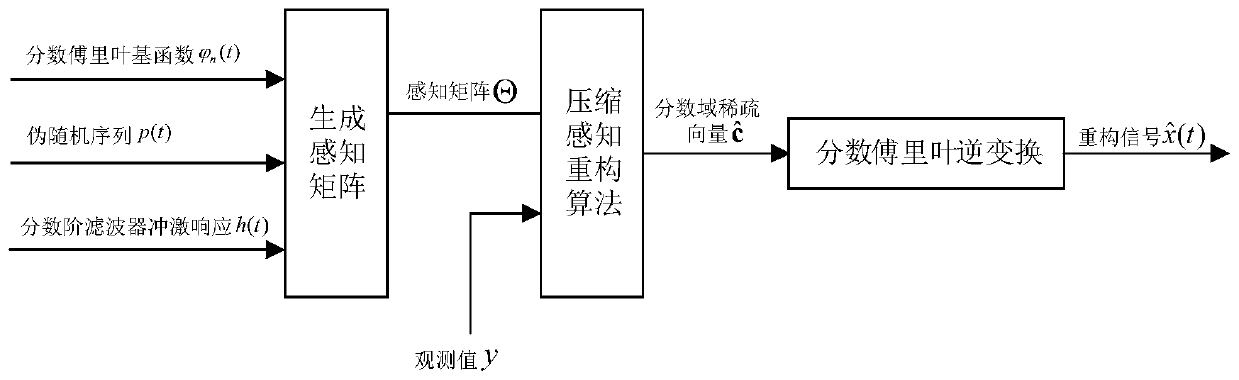
[0072] The invention provides a sparse sampling and reconstruction method of a linear frequency modulation signal based on a fractional Fourier transform domain.

[0073] Step 1: Perform parameter initialization;

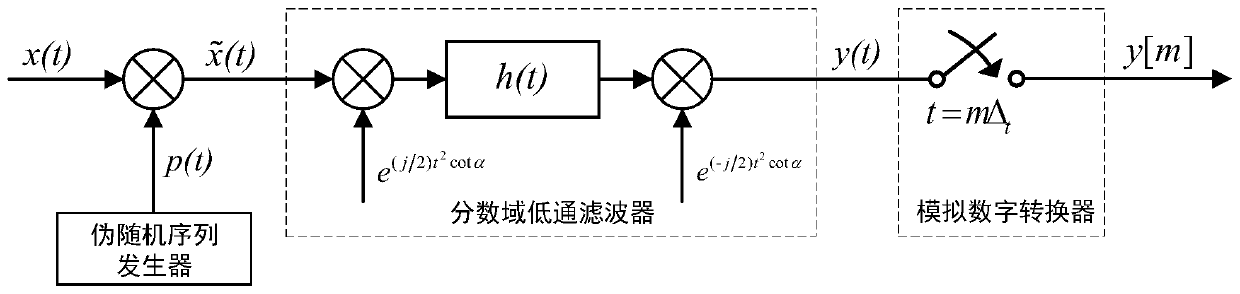
[0074] refer to figure 1 Schematic block diagram of the signal sampling process to construct a sparse representation of an analog chirp signal. For the convenience of analysis, the concept of fractional Fourier transform is introduced first. The fractional Fourier transform of a signal f(t) is defined as

[0075]

[0076] Among them, α is the transformation angle, and the integral kernel K α The expression of (u,t) is

[0077]

[0078] Among them, k is an integer. Correspondingly, the formula of fractional Fourier inverse transform is

[0079]

[0080] Usually, the u-axis is called the fractional Fourier transform domain, and the corresponding variable u is called the fractional order frequency. In particular, when α=π / 2, the fractional Fourier trans...

specific Embodiment 2

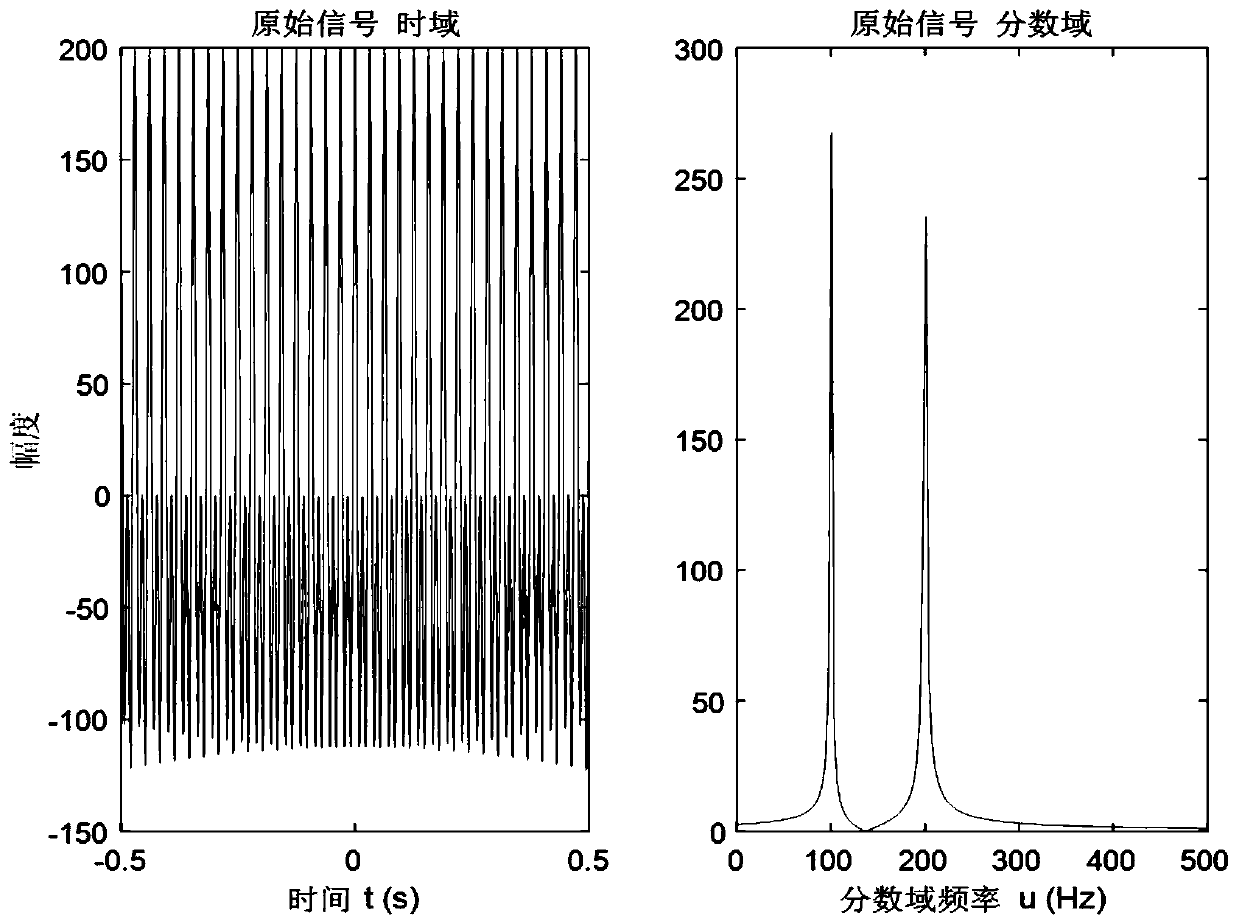
[0146] according to Figure 2 to Figure 6 As shown, this example uses two chirp signals as input signals, where the amplitude of the chirp signals is B=100, and the modulation frequencies are both The central angular frequencies ω are 200Hz and 400Hz, respectively. From the above derivation, it can be seen that the energy of the signal is best gathered in the fractional domain where the rotation angle is α=π / 6, and it is an impulse function at u=ωsinα=100Hz and 200Hz, which is consistent with the simulation results in .

[0147] The chirp signal x(t) is then multiplied by the pseudo-random code c(t). The pseudo-random sequence c(t) in this example is the m-sequence generated by the longest linear shift register, and the period of the pseudo-random sequence is NT c =1, so the interval of spectral lines in the frequency domain is ω 0 =2π / NT c = 2π. As shown, the multiplied signal Its fractional spectrum is moved to every equally spaced frequency point. Consistent with f...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a linear frequency modulation signal sparse sampling and reconstruction method based on a fractional Fourier transform domain. The linear frequency modulation signal sparse sampling and reconstruction method comprises the steps of: carrying out parameter initialization, so that information of an analog chirp signal is reserved at the same time at a low frequency band of apseudo-random code; filtering high-fraction Fourier transform spectrum components of the analog chirp signal and a pseudo-random code signal, and outputting a filtered signal; sampling the output filtered signal by a low-speed analog-to-digital converter to obtain a sampling value; calculating a sparse representation coefficient of the analog chirp signal in a fractional Fourier transform domain through adopting a matching pursuit algorithm; and acquiring an original analog chirp signal at the reconstruction position by means of fractional Fourier transform domain sparse representation. According to the linear frequency modulation signal sparse sampling and reconstruction method, the sparse property of the chirp signal in the fractional Fourier transform domain is utilized, so that the problem that compressed sampling cannot be completed in the frequency domain can be solved.

Description

technical field [0001] The invention relates to the technical field of signal and information processing, and relates to a method for sparse sampling and reconstruction of chirp signals based on fractional Fourier transform domain. Background technique [0002] In today's highly developed information age, digital information is everywhere. The convenience and intelligence brought by digital technology has penetrated into all aspects of social fields such as energy, education, medical care, and community, building people's new digital life, and the digital economy is gradually Become the new engine of my country's economic growth. However, simulation is the nature of nature, and the signals encountered in practice are usually simulated. Sampling is an essential means for the analog physical world to lead to the digital information world, and its theoretical basis is the Shannon-Nyquist sampling theorem. In order to ensure that the information contained in the analog signal i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L27/10G06F7/58G06F17/14H03M7/30
CPCH04L27/103G06F7/582G06F17/14H03M7/30
Inventor 史军宋维斌刘晓萍郑烨镭张成文沙学军
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com